13.2 三角形全等的判定 同步练习(含答案)2024-2025学年华东师大版数学八年级上册
文档属性
| 名称 | 13.2 三角形全等的判定 同步练习(含答案)2024-2025学年华东师大版数学八年级上册 | 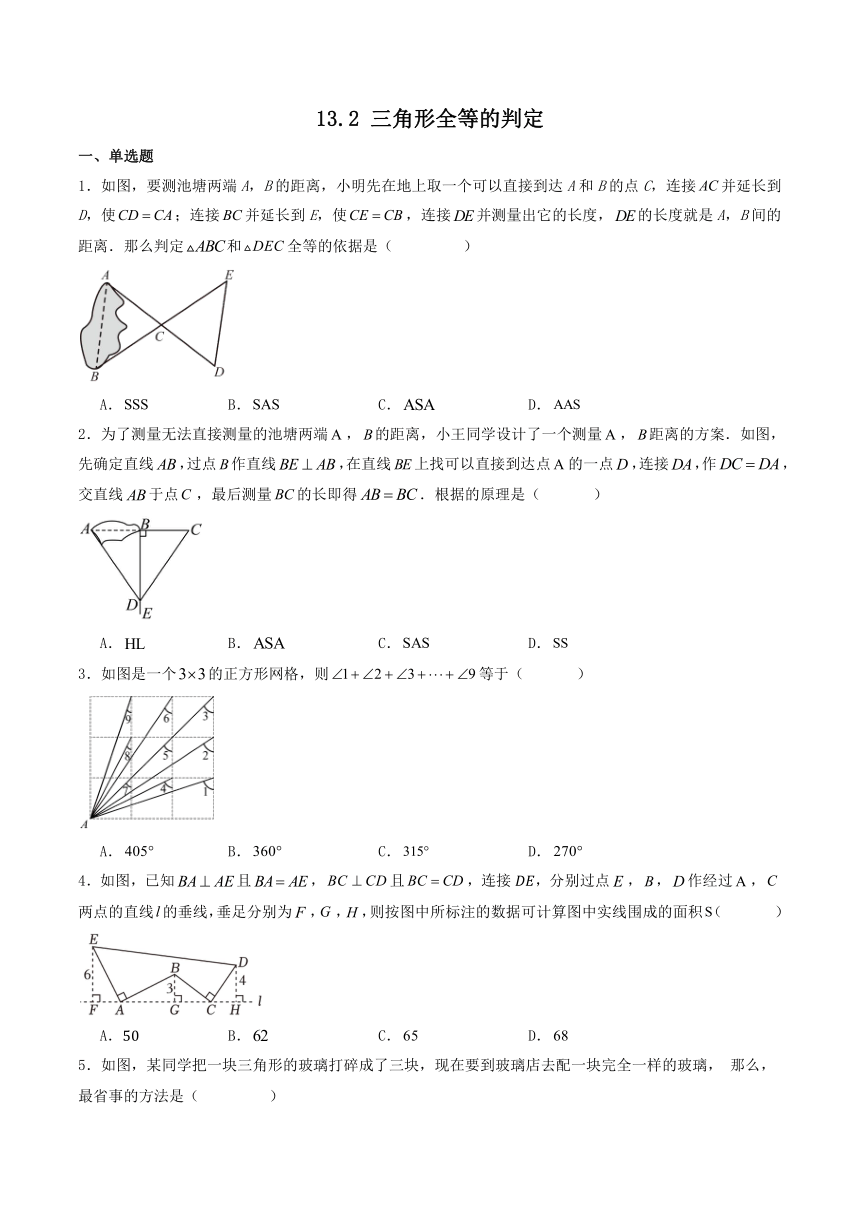 | |
| 格式 | docx | ||
| 文件大小 | 819.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 11:02:49 | ||
图片预览




文档简介
13.2 三角形全等的判定
一、单选题
1.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使,连接并测量出它的长度,的长度就是A,B间的距离.那么判定和全等的依据是( )
A. B. C. D.
2.为了测量无法直接测量的池塘两端,的距离,小王同学设计了一个测量,距离的方案.如图,先确定直线,过点作直线,在直线上找可以直接到达点的一点,连接,作,交直线于点,最后测量的长即得.根据的原理是( )
A. B. C. D.
3.如图是一个的正方形网格,则等于( )
A. B. C. D.
4.如图,已知且,且,连接,分别过点,,作经过,两点的直线的垂线,垂足分别为,,,则按图中所标注的数据可计算图中实线围成的面积( )
A. B. C. D.
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃, 那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
6.如图,在和中,,与相交于点P,则的度数为( )
A. B. C. D.
7.如图,,垂足分别为,与相交于点,且,则下列结论正确的个数为( )
①;②;③;④图中有四对三角形全等.
A.1 B.2 C.3 D.4
8.如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
A. B. C. D.
9.如图,在中,是的角平分线,于点.若点为动点,在点运动的过程中满足,则的最大值为( )
A.28 B.24 C.14 D.7
10.如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,四边形≌四边形,则的大小是 .
12.如图,若,且,,则 .
13.已知如图:,且,于,于,,.连接,.则图中阴影部分的面积为 .
14.如图,是的中线,分别是和延长线上的点,且,连接,则下列说法:①和的面积相等;②;③;④;⑤.其中一定正确的是 (填序号).
15.如图所示,于点,于点.若,且的面积为,则 .
16.如图,点E,F在上,,.请添加一个条件 ,能用说明:.
17.如图,在中,,,.线段,,两点分别在和过点且垂直于的射线上运动,如果以,,三点为顶点的三角形与全等,那么 .
18.如图,,,,点P在线段上以的速度由点A向点B运动,同时,点Q在线段上由点B向点D运动.它们运动的时间为,则点Q的运动速度为 ,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.
19.在中,,,则边上的中线的取值范围是
20.如图,在中,,,为上一点,连接,过作于,连接.若,则的面积为 .
三、解答题
21.公路上,,两站相距千米,、为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得、两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
22.如图,在四边形中,,,,,动点 P 从点 A 出发以每秒1个单位的速度沿向点 D运动,动点Q从点C出发以每秒2个单位的速度沿向点B运动, 同时出发,当点P停止运动时,点Q也随之停止,连接.设点P运动时间为t秒,问当t为何值时, ,并证明.
23.如图,的两条高,交于点,.
(1)求证:;
(2)若,,求的长度.
24.如图,中,,的角平分线、相交于点P,过P作交的延长线于点F,交于点H.
(1)求的度数;
(2)求证:;
(3)求证:.
25.如图,在等腰中,,点从点出发,以的速度沿向点运动,设点的运动时间为.
(1)______.(用的代数式表示)
(2)当点从点开始运动,同时,点从点出发,以的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A A A B D A D D
11. 12. 13.5 14.①③④⑤ 15.12
16. 17.6或8 18.1或 19. 20.8
21.解:∵,
∴,
∵于点,于点,
∴,
∴,
∴,
∵、两所学校到的距离相等,
∴,
在和BCH中,
,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴.
∴应建在距离站千米处,学校到公路的距离是千米.
22.解:如图,由题意得,, ,
,
当时,即,,
当时,,理由如下:
,
,
在和中,
,.
23.(1)证明:∵ABC的两条高,交于点,
∴,
∴,
∴,
在和中,
,∴;
(2)解:∵,,
∴,,
∵,,
∴.
24.(1)解:中,,
,
∵平分,平分,
∴,,
∴,
∴;
(2)证明:∵,
∴,
∵,
,
∴,
,
∵平分,
,
在和中,
,∴;
(3)证明:∵,
∴,,,
∵平分,
∴,
∴,
∵,
∴,
在APH和中,
,∴,
∴,
∵,
∴.
25.(1)解:依题意,得,
∴.故答案为:;
(2)解:①当,时,,
∵,
∴,
∴,
,解得:,,
,解得:;
②当时,,
∵,
∴,
,解得:,
,,解得:.
综上所述:当或时,与全等.
一、单选题
1.如图,要测池塘两端A,B的距离,小明先在地上取一个可以直接到达A和B的点C,连接并延长到D,使;连接并延长到E,使,连接并测量出它的长度,的长度就是A,B间的距离.那么判定和全等的依据是( )
A. B. C. D.
2.为了测量无法直接测量的池塘两端,的距离,小王同学设计了一个测量,距离的方案.如图,先确定直线,过点作直线,在直线上找可以直接到达点的一点,连接,作,交直线于点,最后测量的长即得.根据的原理是( )
A. B. C. D.
3.如图是一个的正方形网格,则等于( )
A. B. C. D.
4.如图,已知且,且,连接,分别过点,,作经过,两点的直线的垂线,垂足分别为,,,则按图中所标注的数据可计算图中实线围成的面积( )
A. B. C. D.
5.如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃, 那么,最省事的方法是( )
A.带①去 B.带②去 C.带③去 D.带①去和带②去
6.如图,在和中,,与相交于点P,则的度数为( )
A. B. C. D.
7.如图,,垂足分别为,与相交于点,且,则下列结论正确的个数为( )
①;②;③;④图中有四对三角形全等.
A.1 B.2 C.3 D.4
8.如图,小虎用10块高度都是的相同长方体小木块,垒了两堵与地面垂直的木墙,木墙之间刚好可以放进一个等腰直角三角板(,),点在上,点和分别与木墙的顶端重合,则两堵木墙之间的距离的长度为( )
A. B. C. D.
9.如图,在中,是的角平分线,于点.若点为动点,在点运动的过程中满足,则的最大值为( )
A.28 B.24 C.14 D.7
10.如图,是的中线,E,F分别是和延长线上的点,且,连接.则下列说法:①;②和面积相等;③; ④.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,四边形≌四边形,则的大小是 .
12.如图,若,且,,则 .
13.已知如图:,且,于,于,,.连接,.则图中阴影部分的面积为 .
14.如图,是的中线,分别是和延长线上的点,且,连接,则下列说法:①和的面积相等;②;③;④;⑤.其中一定正确的是 (填序号).
15.如图所示,于点,于点.若,且的面积为,则 .
16.如图,点E,F在上,,.请添加一个条件 ,能用说明:.
17.如图,在中,,,.线段,,两点分别在和过点且垂直于的射线上运动,如果以,,三点为顶点的三角形与全等,那么 .
18.如图,,,,点P在线段上以的速度由点A向点B运动,同时,点Q在线段上由点B向点D运动.它们运动的时间为,则点Q的运动速度为 ,使得A、C、P三点构成的三角形与B、P、Q三点构成的三角形全等.
19.在中,,,则边上的中线的取值范围是
20.如图,在中,,,为上一点,连接,过作于,连接.若,则的面积为 .
三、解答题
21.公路上,,两站相距千米,、为两所学校,于点,于点,如图,已知千米,现在要在公路上建一报亭,使得、两所学校到的距离相等,且,问:应建在距离站多远处?学校到公路的距离是多少千米?
22.如图,在四边形中,,,,,动点 P 从点 A 出发以每秒1个单位的速度沿向点 D运动,动点Q从点C出发以每秒2个单位的速度沿向点B运动, 同时出发,当点P停止运动时,点Q也随之停止,连接.设点P运动时间为t秒,问当t为何值时, ,并证明.
23.如图,的两条高,交于点,.
(1)求证:;
(2)若,,求的长度.
24.如图,中,,的角平分线、相交于点P,过P作交的延长线于点F,交于点H.
(1)求的度数;
(2)求证:;
(3)求证:.
25.如图,在等腰中,,点从点出发,以的速度沿向点运动,设点的运动时间为.
(1)______.(用的代数式表示)
(2)当点从点开始运动,同时,点从点出发,以的速度沿向点运动,是否存在这样的值,使得与全等?若存在,请求出的值;若不存在,请说明理由.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 B A A A A B D A D D
11. 12. 13.5 14.①③④⑤ 15.12
16. 17.6或8 18.1或 19. 20.8
21.解:∵,
∴,
∵于点,于点,
∴,
∴,
∴,
∵、两所学校到的距离相等,
∴,
在和BCH中,
,
∴,
∴,,
∵,
∴,
∵,,
∴,
∴.
∴应建在距离站千米处,学校到公路的距离是千米.
22.解:如图,由题意得,, ,
,
当时,即,,
当时,,理由如下:
,
,
在和中,
,.
23.(1)证明:∵ABC的两条高,交于点,
∴,
∴,
∴,
在和中,
,∴;
(2)解:∵,,
∴,,
∵,,
∴.
24.(1)解:中,,
,
∵平分,平分,
∴,,
∴,
∴;
(2)证明:∵,
∴,
∵,
,
∴,
,
∵平分,
,
在和中,
,∴;
(3)证明:∵,
∴,,,
∵平分,
∴,
∴,
∵,
∴,
在APH和中,
,∴,
∴,
∵,
∴.
25.(1)解:依题意,得,
∴.故答案为:;
(2)解:①当,时,,
∵,
∴,
∴,
,解得:,,
,解得:;
②当时,,
∵,
∴,
,解得:,
,,解得:.
综上所述:当或时,与全等.
