第23章 解直角三角形 单元模拟测试卷(含答案)2024-2025学年沪科版九年级数学上册
文档属性
| 名称 | 第23章 解直角三角形 单元模拟测试卷(含答案)2024-2025学年沪科版九年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 00:00:00 | ||
图片预览



文档简介
沪科版九年级数学上册第23章解直角三角形 单元模拟测试卷
一、单选题(共10题;共40分)
1.(4分)cos60°的值等于( )
A. B. C. D.
2.(4分)的值等于( )
A. B.1 C. D.
3.(4分) 如果把三边的长度都扩大为原来的倍,那么锐角的四个三角比的值( )
A.都扩大为原来的倍 B.都缩小为原来的
C.都没有变化 D.都不能确定
4.(4分)如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )
A. B. C. D.
5.(4分)估计的值在( )
A.2与3之间 B.3与4之间 C.4与5之间 D.5与6之间
6.(4分)如图,在和中,,,,,若,则的面积为( )
A.8 B.16 C.18 D.24
7.(4分)如图,在平面直角坐标系中,点P在反比例函数的图象上,点A,B在x轴上,且,交y轴于点C,.若的面积是4,则k的值是( )
A.1 B.2 C. D.
8.(4分)如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.m B.m C.8m D.4m
9.(4分)如图,在中,,,,分别以点,为圆心,大于的长为半径画弧,两弧相交于点,,过,两点作直线交于点,则的长为( )
A. B.4 C. D.5
10.(4分)任意一张正方形先对折再翻折然后加上废旧的草杆就能做成一个简易的纸风车,迎着风就会哗啦啦转动起来,小小的纸风车带来童年满满的回忆.如图是彤彤折叠的一个纸风车,风车由四个全等的直角三角形组成,其中∠DOG 为90°.延长直角三角形的斜边,恰好交于四个直角三角形的斜边中点,若,那么这个风车的面积为( )
A. B. C. D.
二、填空题(共4题;共20分)
11.(5分)如图,小明一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶一段距离至B地,再沿北偏东方向行驶千米到达风景区C,小明发现风景区C在A地的北偏东方向,那么A,B两地的距离为 千米.
12.(5分)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度,无人机在空中点P处,测得点P距地面上点A为80米,点A处的俯角为,楼顶C点处的俯角为,已知点A与大楼的距离为70米(点A,B,C,P在同一平面内),则大楼的高度为 (结果保留根号).
13.(5分) 如图,,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,,,.若点到点的距离,求图中及盲区中的长度.(参考数据:,,,)
答:
(1)(2分)图中的长度是 米
(2)(3分)盲区中DE的长度是 米
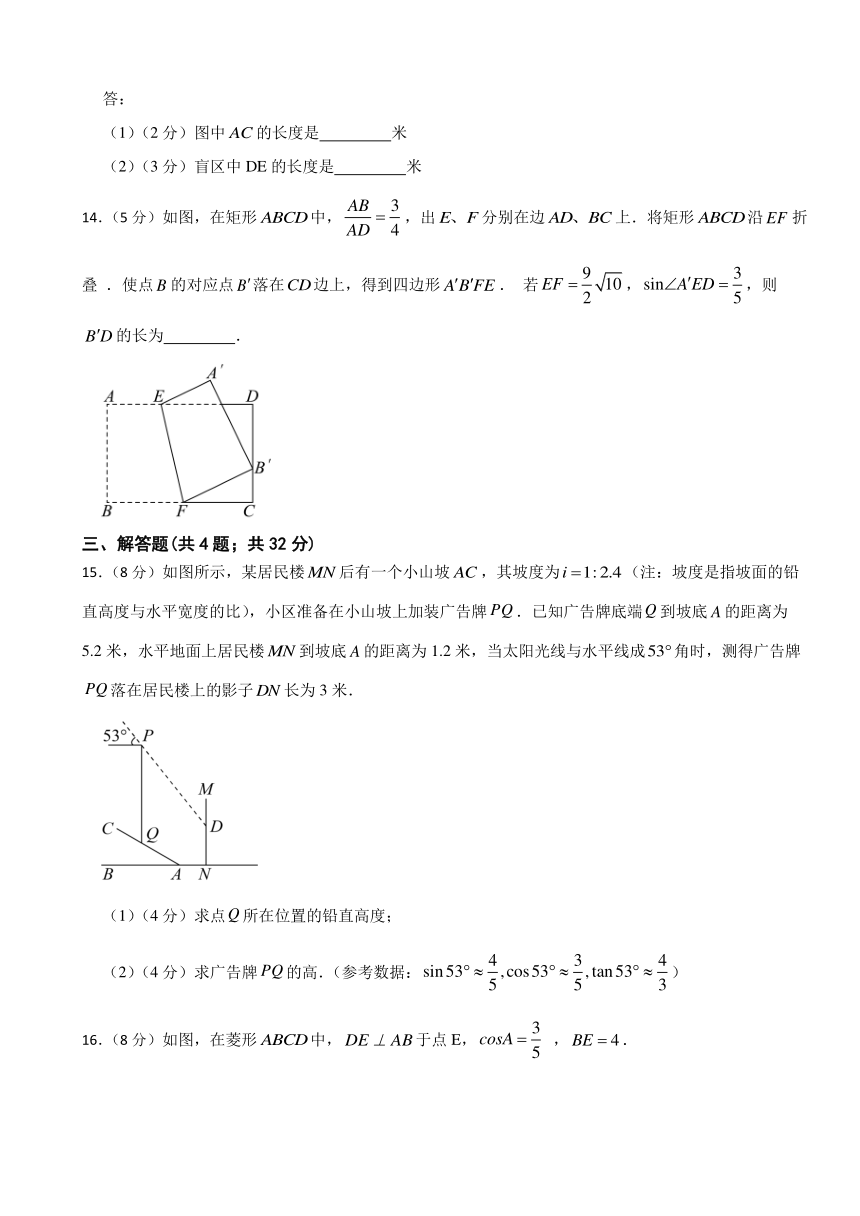
14.(5分)如图,在矩形中,,出分别在边上.将矩形沿折叠 .使点的对应点落在边上,得到四边形. 若,,则的长为 .
三、解答题(共4题;共32分)
15.(8分)如图所示,某居民楼后有一个小山坡,其坡度为(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌.已知广告牌底端到坡底的距离为5.2米,水平地面上居民楼到坡底的距离为1.2米,当太阳光线与水平线成角时,测得广告牌落在居民楼上的影子长为3米.
(1)(4分)求点所在位置的铅直高度;
(2)(4分)求广告牌的高.(参考数据:)
16.(8分)如图,在菱形中,于点E, ,.
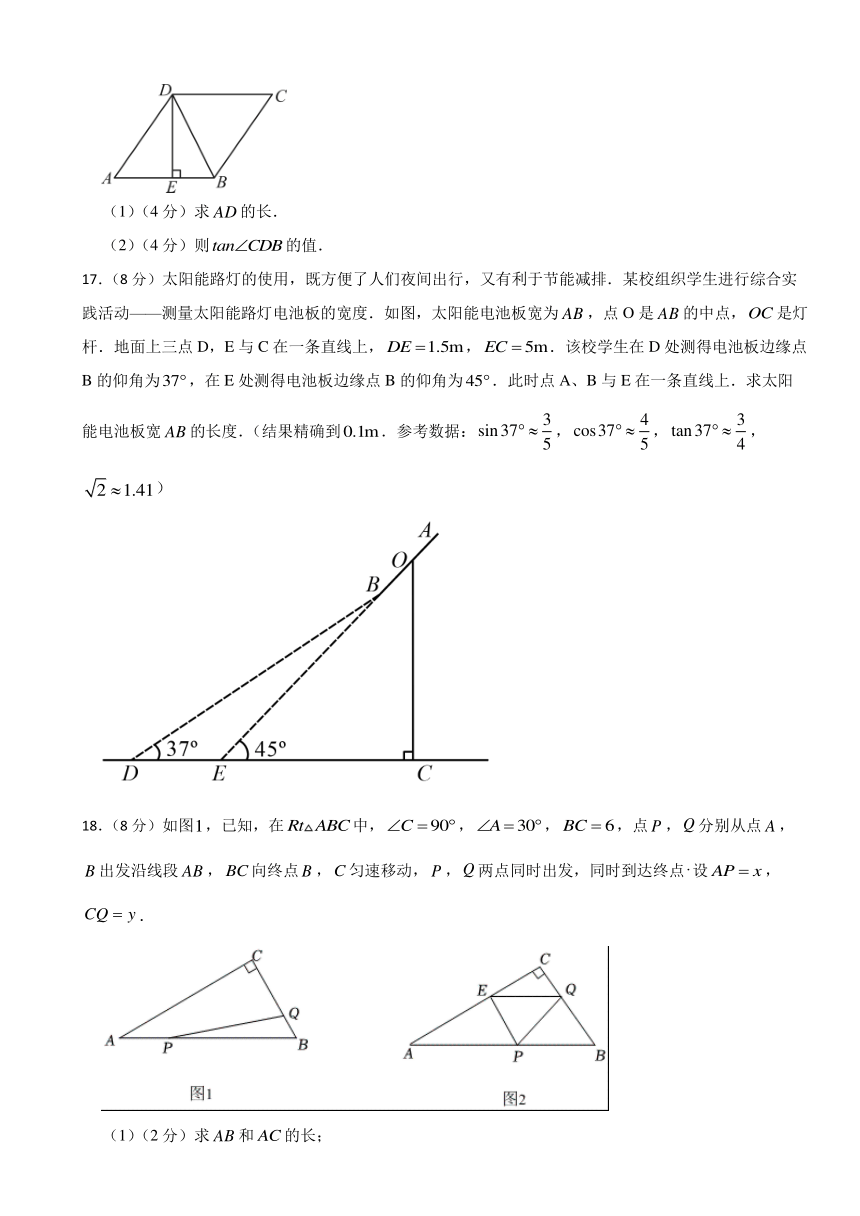
(1)(4分)求的长.
(2)(4分)则的值.
17.(8分)太阳能路灯的使用,既方便了人们夜间出行,又有利于节能减排.某校组织学生进行综合实践活动——测量太阳能路灯电池板的宽度.如图,太阳能电池板宽为,点O是的中点,是灯杆.地面上三点D,E与C在一条直线上,,.该校学生在D处测得电池板边缘点B的仰角为,在E处测得电池板边缘点B的仰角为.此时点A、B与E在一条直线上.求太阳能电池板宽的长度.(结果精确到.参考数据:,,,)
18.(8分)如图,已知,在中,,,,点,分别从点,出发沿线段,向终点,匀速移动,,两点同时出发,同时到达终点设,.
(1)(2分)求和的长;
(2)(3分)求关于的函数表达式;
(3)(3分)如图,过点作于点,连接,.
当为直角三角形时,求的值;
作点关于的对称点,当点落在的延长线上时,求的值.
四、综合题(共5题;共58分)
19.(10分)如图,一架无人机沿水平直线飞行进行测绘工作.无人机悬停在P 处,测得前方水平地面上大树的顶端B 的俯角为,同时还测得前方某建筑物的顶端D的俯角为.已知点A,B,C,D,P 在同一平面内,大树的高度为,建筑物的高度 为,大树与建筑物的距离为,求无人机在P 处时离地面的高度(参考数据: ,).
20.(10分)某班学生为了测量学校旗杆的高度,设计了以下测量方法,如图,小明同学站在旗杆正前方处看旗杆顶端的仰角为,看处的仰角为,已知小明的眼睛与地面距离,红旗宽为,求旗杆的高度.(结果保留一位小数,参考数据,).
21.(12分)年月日是我国第个“全国消防宣传日”,该年“消防宣传月”活动的主题是“落实消防责任,防范安全风险”.为落实该主题,济南市消防大队到建东小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点A在一定范围内转动,张角为(),转动点A距离地面的高度为.
(1)(6分)当起重臂长度为,张角,求云梯消防车最高点C距离地面
的高度;
(2)(6分)已知该小区层高为,若某居民家突发险情,请问该消防车有效救援能达到几层?请说明理由.(结果精确到,参考数据:,,,)
22.(12分)在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔前有一座高为的观景台,已知,,点、、在同一水平线上.某学习小组在观景台处测得塔顶部的仰角为,在观景台处测得塔顶部的仰角为,求塔的高度(精确到).(参考数据:,,,,).
23.(14分)如图,直线与轴、轴分别交于、两点,抛物线过、两点.
(1)(4分)求抛物线的解析式;
(2)(4分)点为抛物线上位于上方的一点,过点作于点,作轴交于点,当的周长最大时,求点的坐标;
(3)(6分)是平面内的一点,在(2)的条件下,将绕点顺时针旋转得到,当时,的两个顶点恰好落在抛物线上,求点的横坐标.
答案解析部分
1.【答案】D
【解析】【解答】解:cos60°=,
故选:D.
【分析】根据特殊角的三角函数值可求解.
2.【答案】D
【解析】【解答】解:;
故答案为:D.
【分析】利用特殊角的三角函数值求解即可。
3.【答案】C
【解析】【解答】解: ∵把三边的长度都扩大为原来的倍,锐角A的大小不变,
∴锐角的四个三角比的值都没有变化,
故答案为:C.
【分析】结合题意,根据锐角三角函数的定义判断求解即可。
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
【解析】【解答】解:如图,过点C作CE⊥BC
∵∠ABC=150°
∴∠CBE=30°
∴
故答案为:D.
【分析】过点C作CE⊥BC,根据邻补角的性质可得∠CBE=30°,然后根据三角函数的概念进行计算.
9.【答案】B
10.【答案】A
11.【答案】4
12.【答案】米
13.【答案】(1)1.12
(2)2.8
【解析】【解答】解:(1)在Rt△ABC中,sin∠B=sin43°==0.7,
∴AC=1.12m;
故答案为:1.12;
(2)∵AC⊥BE,DF⊥BE,
∴AC∥DF,又AF∥BE,
∴ACDF为平行四边形,
∴DF=AC=1.12m,
在Rt△EFD中,tan∠E=tan20°=0.4,
∴=0.4,
又DF=1.12m,
∴DE=2.8m.
故答案为:2.8.
【分析】(1)在Rt△ABC中,利用∠B的正弦函数即可求出AC的长;
(2)首先判断出ACDF为平行四边形,得DF=AC,进而在△DEF中,由∠E的正切函数定义可求出DE的长.
14.【答案】
15.【答案】(1)2米
(2)9米
16.【答案】(1)解:,,
,
设,则,
菱形,
,
,
解得,
;
(2)解:,
由(1)可得,
在,由勾股定理可得,
菱形,
,
,
,
.
【解析】【分析】(1)首先根据三角函数的定义,根据 , 可得出 ,所以可设,则,再根据菱形的性质可得方程,解方程得x=2,进一步求得AD=10即可;
(2)根据(1)可得AD=10,AE=6,根据勾股定理可求得DE=8,从而可求得tan∠DBE=,进一步得出=tan∠DBE=2即可。
17.【答案】
18.【答案】(1)解:,,,
,
,
(2)解:由题意可设,
当时,,当时,;
,解得,
关于的函数表达式为;
(3)解:,
,
,
,
为直角三角形,可分为两种情况.
当时,如图,
,
,
,
,
,
即,
;
当时,如图,
,,
,
,
四边形为平行四边形,
,
,
,
,
,
;
综上所述,为或;
当点落在的延长线上时,如图,
,
,
又由对称可知:,
,
为等边三角形,
同理可得为等边三角形,
,
又,
,
.
【解析】【分析】本题考查了等腰三角形的分类,勾股定理,一次函数,解直角三角形,解决本问题需要较强的计算能力.
(1)先求出的长,进一步求出结果;
(2)设出函数解析式,将点代入解析式,进而求出结果;
(3)根据题意先判断出为直角三角形,再作出为直角三角形的两种图形,进而解直角三角形可求出的值,第二小问判断出当点落在的延长线上时,由对称知识判断出为等边三角形,进而求出的值.
19.【答案】无人机在处时离地面的高度
20.【答案】旗杆的高度约为
21.【答案】(1)解:如图所示,过点C作,垂足为F,过点A作,垂足为G,
则,,
∵,
∴,
在中,,,
∴(),
∴(),
∴云梯消防车最高点C距离地面的高度为.
(2)解:该消防车能有效救援层,理由如下,
当,时,能达到最高高度,
∵,
∴,
在中,,
∴(),
∴(),
∵,
∴该消防车能有效救援层.
【解析】【分析】 (1)过点C作,垂足为F,过点A作,垂足为G, 根据矩形的性质可得,,,在中,,,
则(),根据可求得云梯消防车最高点C距离地面的高度;
(2)由题意可知:当,时,能达到最高高度,由可得,
在中,,可求出CG,再根据求出CF即可。
22.【答案】
23.【答案】(1)解:,令,
得,
解得:,
令,得,
,,
故得方程组,
,
此抛物线的解析式为:;
(2)解:,,
,,
,
,,
轴,
,
,
,
,
,
,
,
设,则,
,
,
∴当时,的周长最大,
,,
∴;
(3)解:当时,,
∴,,
,
当顺时针旋转后,轴,轴,
设则,,
①当、两个顶点在抛物线上时,
,
解得:,
的横坐标为,
②当、两个顶点在抛物线上时,
,
解得:,
的横坐标为,
又轴,
、不会同时在抛物线上,
综上所述,点的横坐标为或.
【解析】【分析】(1)根据题目所给条件求出点A,点B的坐标,再根据待定系数法求出抛物线的解析式。
(2)根据勾股定理得出AB的长,以及由锐角三角函数得出 , ,设,则,,根据周长公式可以列式为 ,最后得出答案。
(3)设则,
①当、两个顶点在抛物线上时, 可列式为
②当、两个顶点在抛物线上时,列式为
,最后得出答案。
一、单选题(共10题;共40分)
1.(4分)cos60°的值等于( )
A. B. C. D.
2.(4分)的值等于( )
A. B.1 C. D.
3.(4分) 如果把三边的长度都扩大为原来的倍,那么锐角的四个三角比的值( )
A.都扩大为原来的倍 B.都缩小为原来的
C.都没有变化 D.都不能确定
4.(4分)如图,O为跷跷板AB的中点.支柱OC与地面MN垂直,垂足为点C,当跷跷板的一端B着地时,跷跷板AB与地面MN的夹角为20°,测得AB=1.6m,则OC的长为( )
A. B. C. D.
5.(4分)估计的值在( )
A.2与3之间 B.3与4之间 C.4与5之间 D.5与6之间
6.(4分)如图,在和中,,,,,若,则的面积为( )
A.8 B.16 C.18 D.24
7.(4分)如图,在平面直角坐标系中,点P在反比例函数的图象上,点A,B在x轴上,且,交y轴于点C,.若的面积是4,则k的值是( )
A.1 B.2 C. D.
8.(4分)如图,某商场一楼与二楼之间的电梯示意图.∠ABC=150°,BC的长是8m,则乘电梯从点B到点C上升的高度h是( )
A.m B.m C.8m D.4m
9.(4分)如图,在中,,,,分别以点,为圆心,大于的长为半径画弧,两弧相交于点,,过,两点作直线交于点,则的长为( )
A. B.4 C. D.5
10.(4分)任意一张正方形先对折再翻折然后加上废旧的草杆就能做成一个简易的纸风车,迎着风就会哗啦啦转动起来,小小的纸风车带来童年满满的回忆.如图是彤彤折叠的一个纸风车,风车由四个全等的直角三角形组成,其中∠DOG 为90°.延长直角三角形的斜边,恰好交于四个直角三角形的斜边中点,若,那么这个风车的面积为( )
A. B. C. D.
二、填空题(共4题;共20分)
11.(5分)如图,小明一家自驾到风景区C游玩,到达A地后,导航显示车辆应沿北偏西方向行驶一段距离至B地,再沿北偏东方向行驶千米到达风景区C,小明发现风景区C在A地的北偏东方向,那么A,B两地的距离为 千米.
12.(5分)无人机在实际生活中的应用越来越广泛.如图所示,某人利用无人机测量大楼的高度,无人机在空中点P处,测得点P距地面上点A为80米,点A处的俯角为,楼顶C点处的俯角为,已知点A与大楼的距离为70米(点A,B,C,P在同一平面内),则大楼的高度为 (结果保留根号).
13.(5分) 如图,,区域为驾驶员的盲区,驾驶员视线与地面的夹角,视线与地面的夹角,点为视线与车窗底端的交点,,,.若点到点的距离,求图中及盲区中的长度.(参考数据:,,,)
答:
(1)(2分)图中的长度是 米
(2)(3分)盲区中DE的长度是 米
14.(5分)如图,在矩形中,,出分别在边上.将矩形沿折叠 .使点的对应点落在边上,得到四边形. 若,,则的长为 .
三、解答题(共4题;共32分)
15.(8分)如图所示,某居民楼后有一个小山坡,其坡度为(注:坡度是指坡面的铅直高度与水平宽度的比),小区准备在小山坡上加装广告牌.已知广告牌底端到坡底的距离为5.2米,水平地面上居民楼到坡底的距离为1.2米,当太阳光线与水平线成角时,测得广告牌落在居民楼上的影子长为3米.
(1)(4分)求点所在位置的铅直高度;
(2)(4分)求广告牌的高.(参考数据:)
16.(8分)如图,在菱形中,于点E, ,.
(1)(4分)求的长.
(2)(4分)则的值.
17.(8分)太阳能路灯的使用,既方便了人们夜间出行,又有利于节能减排.某校组织学生进行综合实践活动——测量太阳能路灯电池板的宽度.如图,太阳能电池板宽为,点O是的中点,是灯杆.地面上三点D,E与C在一条直线上,,.该校学生在D处测得电池板边缘点B的仰角为,在E处测得电池板边缘点B的仰角为.此时点A、B与E在一条直线上.求太阳能电池板宽的长度.(结果精确到.参考数据:,,,)
18.(8分)如图,已知,在中,,,,点,分别从点,出发沿线段,向终点,匀速移动,,两点同时出发,同时到达终点设,.
(1)(2分)求和的长;
(2)(3分)求关于的函数表达式;
(3)(3分)如图,过点作于点,连接,.
当为直角三角形时,求的值;
作点关于的对称点,当点落在的延长线上时,求的值.
四、综合题(共5题;共58分)
19.(10分)如图,一架无人机沿水平直线飞行进行测绘工作.无人机悬停在P 处,测得前方水平地面上大树的顶端B 的俯角为,同时还测得前方某建筑物的顶端D的俯角为.已知点A,B,C,D,P 在同一平面内,大树的高度为,建筑物的高度 为,大树与建筑物的距离为,求无人机在P 处时离地面的高度(参考数据: ,).
20.(10分)某班学生为了测量学校旗杆的高度,设计了以下测量方法,如图,小明同学站在旗杆正前方处看旗杆顶端的仰角为,看处的仰角为,已知小明的眼睛与地面距离,红旗宽为,求旗杆的高度.(结果保留一位小数,参考数据,).
21.(12分)年月日是我国第个“全国消防宣传日”,该年“消防宣传月”活动的主题是“落实消防责任,防范安全风险”.为落实该主题,济南市消防大队到建东小区进行消防演习.已知,图1是一辆登高云梯消防车的实物图,图2是其工作示意图,起重臂可伸缩(),且起重臂可绕点A在一定范围内转动,张角为(),转动点A距离地面的高度为.
(1)(6分)当起重臂长度为,张角,求云梯消防车最高点C距离地面
的高度;
(2)(6分)已知该小区层高为,若某居民家突发险情,请问该消防车有效救援能达到几层?请说明理由.(结果精确到,参考数据:,,,)
22.(12分)在综合与实践活动中,要利用测角仪测量塔的高度.如图,塔前有一座高为的观景台,已知,,点、、在同一水平线上.某学习小组在观景台处测得塔顶部的仰角为,在观景台处测得塔顶部的仰角为,求塔的高度(精确到).(参考数据:,,,,).
23.(14分)如图,直线与轴、轴分别交于、两点,抛物线过、两点.
(1)(4分)求抛物线的解析式;
(2)(4分)点为抛物线上位于上方的一点,过点作于点,作轴交于点,当的周长最大时,求点的坐标;
(3)(6分)是平面内的一点,在(2)的条件下,将绕点顺时针旋转得到,当时,的两个顶点恰好落在抛物线上,求点的横坐标.
答案解析部分
1.【答案】D
【解析】【解答】解:cos60°=,
故选:D.
【分析】根据特殊角的三角函数值可求解.
2.【答案】D
【解析】【解答】解:;
故答案为:D.
【分析】利用特殊角的三角函数值求解即可。
3.【答案】C
【解析】【解答】解: ∵把三边的长度都扩大为原来的倍,锐角A的大小不变,
∴锐角的四个三角比的值都没有变化,
故答案为:C.
【分析】结合题意,根据锐角三角函数的定义判断求解即可。
4.【答案】B
5.【答案】B
6.【答案】D
7.【答案】B
8.【答案】D
【解析】【解答】解:如图,过点C作CE⊥BC
∵∠ABC=150°
∴∠CBE=30°
∴
故答案为:D.
【分析】过点C作CE⊥BC,根据邻补角的性质可得∠CBE=30°,然后根据三角函数的概念进行计算.
9.【答案】B
10.【答案】A
11.【答案】4
12.【答案】米
13.【答案】(1)1.12
(2)2.8
【解析】【解答】解:(1)在Rt△ABC中,sin∠B=sin43°==0.7,
∴AC=1.12m;
故答案为:1.12;
(2)∵AC⊥BE,DF⊥BE,
∴AC∥DF,又AF∥BE,
∴ACDF为平行四边形,
∴DF=AC=1.12m,
在Rt△EFD中,tan∠E=tan20°=0.4,
∴=0.4,
又DF=1.12m,
∴DE=2.8m.
故答案为:2.8.
【分析】(1)在Rt△ABC中,利用∠B的正弦函数即可求出AC的长;
(2)首先判断出ACDF为平行四边形,得DF=AC,进而在△DEF中,由∠E的正切函数定义可求出DE的长.
14.【答案】
15.【答案】(1)2米
(2)9米
16.【答案】(1)解:,,
,
设,则,
菱形,
,
,
解得,
;
(2)解:,
由(1)可得,
在,由勾股定理可得,
菱形,
,
,
,
.
【解析】【分析】(1)首先根据三角函数的定义,根据 , 可得出 ,所以可设,则,再根据菱形的性质可得方程,解方程得x=2,进一步求得AD=10即可;
(2)根据(1)可得AD=10,AE=6,根据勾股定理可求得DE=8,从而可求得tan∠DBE=,进一步得出=tan∠DBE=2即可。
17.【答案】
18.【答案】(1)解:,,,
,
,
(2)解:由题意可设,
当时,,当时,;
,解得,
关于的函数表达式为;
(3)解:,
,
,
,
为直角三角形,可分为两种情况.
当时,如图,
,
,
,
,
,
即,
;
当时,如图,
,,
,
,
四边形为平行四边形,
,
,
,
,
,
;
综上所述,为或;
当点落在的延长线上时,如图,
,
,
又由对称可知:,
,
为等边三角形,
同理可得为等边三角形,
,
又,
,
.
【解析】【分析】本题考查了等腰三角形的分类,勾股定理,一次函数,解直角三角形,解决本问题需要较强的计算能力.
(1)先求出的长,进一步求出结果;
(2)设出函数解析式,将点代入解析式,进而求出结果;
(3)根据题意先判断出为直角三角形,再作出为直角三角形的两种图形,进而解直角三角形可求出的值,第二小问判断出当点落在的延长线上时,由对称知识判断出为等边三角形,进而求出的值.
19.【答案】无人机在处时离地面的高度
20.【答案】旗杆的高度约为
21.【答案】(1)解:如图所示,过点C作,垂足为F,过点A作,垂足为G,
则,,
∵,
∴,
在中,,,
∴(),
∴(),
∴云梯消防车最高点C距离地面的高度为.
(2)解:该消防车能有效救援层,理由如下,
当,时,能达到最高高度,
∵,
∴,
在中,,
∴(),
∴(),
∵,
∴该消防车能有效救援层.
【解析】【分析】 (1)过点C作,垂足为F,过点A作,垂足为G, 根据矩形的性质可得,,,在中,,,
则(),根据可求得云梯消防车最高点C距离地面的高度;
(2)由题意可知:当,时,能达到最高高度,由可得,
在中,,可求出CG,再根据求出CF即可。
22.【答案】
23.【答案】(1)解:,令,
得,
解得:,
令,得,
,,
故得方程组,
,
此抛物线的解析式为:;
(2)解:,,
,,
,
,,
轴,
,
,
,
,
,
,
,
设,则,
,
,
∴当时,的周长最大,
,,
∴;
(3)解:当时,,
∴,,
,
当顺时针旋转后,轴,轴,
设则,,
①当、两个顶点在抛物线上时,
,
解得:,
的横坐标为,
②当、两个顶点在抛物线上时,
,
解得:,
的横坐标为,
又轴,
、不会同时在抛物线上,
综上所述,点的横坐标为或.
【解析】【分析】(1)根据题目所给条件求出点A,点B的坐标,再根据待定系数法求出抛物线的解析式。
(2)根据勾股定理得出AB的长,以及由锐角三角函数得出 , ,设,则,,根据周长公式可以列式为 ,最后得出答案。
(3)设则,
①当、两个顶点在抛物线上时, 可列式为
②当、两个顶点在抛物线上时,列式为
,最后得出答案。
