选择必修第二册 第四章 4.1 数列的概念(第1课时) 课件(共24张PPT)
文档属性
| 名称 | 选择必修第二册 第四章 4.1 数列的概念(第1课时) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 07:36:32 | ||
图片预览








文档简介
(共24张PPT)
选择必修
第四章 数列
4.1 数列的概念(第1课时)
教学目标
学习目标 数学素养
1.理解数列的有关概念与数列的表示方法. 1.逻辑推理素养.
2.掌握数列的分类,了解数列的单调性. 2.数学抽象素养.
3.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.逻辑推理素养和数学运算素养.
本章引入
第四章 数列
对数列的研究源于现实生产、生活的需要. 例如,一棵树在某一时刻的高度是2m,如果在每年的同-时刻都记录下这棵树的高度,并按先后顺序排列起来,就得到一列数.人们常用这样的一列数有序地表达一类事物,或者记录一个过程.像这样按照确定的顺序排列的一列数称为数列.如果用正整数表示事物发展过程的先后顺序,并且把这样的正整数看作自变量的取值,把事物的对应数值看作相应的函数值,那么数列就是定义在正整数集(或正整数集的有限子集)上的一类离散函数.
本章我们将学习数列的概念和表示方法,并研究两类特殊的数列——等差数列和等比数列,探索它们的取值规律,建立它们的通项公式、前n项和公式,并应用它们解决一些问题. 我们将把数列看成一类特殊的函数,并用函数的思想方法研究数列. 我们还将学习数学归纳法,这是一种证明与正整数有关的数学命题的特殊方法.在本章的学习中,我们可以体验通过数学抽象获得一个数学对象,并通过数学运算、逻辑推理等进行研究的过程和方法;通过建立数学模型刻画具有递推规律的事物,提高解决实际问题的能力.
新知探究
4.1 的概念(第1课时)
在现实生活和数学学习中,我们经常需要根据问题的意义,通过对一些数据按特定顺序排列的方法来刻画研究对象.例如:
1.王芳从1岁到17岁,每年生日那天测量身高,将这些身高数据(单位:cm)依次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168. ①
记王芳第i岁时的身高为hi,
那么h1=75,h2=87,……,h17=168.
我们发现,hi 中的i反映了身高按岁数从1到17的顺序排列时的确定位置,h1=75是排在第一位的数,h2=87是排在第二位的数,……,h17 =168是排在第17位的数,
它们之间不能交换位置.
所以,①是具有确定顺序的一列数.
知新引入
记第i天月亮可见部分的数为si,那么s1=5,s2=10,…,s15=240. 这里,si中的i反映了月亮可见部分的数按日期从1到15的顺序排列时的确定位置,即s1=5是排在第1位的数,s2=10是排在第2位的数,…,s15=240是排在第15位的数,
2. 在两河流域发掘的一块泥版上就有一列依次表示一个月中从第1天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240 ②
把满月分成240份,则从初一到十五每天月亮的可见部分可用一个代表份数的数来表示.
它们之间不能交换位置.
所以,②也是具有确定顺序的一列数.
知新探究
- -,… ③
记i次幂为ai ,那么a1 =- ,a2 = ,…,这里ai 中的i反映了从1到n按顺序排列时的确定位置,a1 =-是排第一位的数,a2= 是排在第二位的数,…
3.的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
.
它们之间不能交换位置.
所以,③也是具有确定顺序的一列数.
上述例子的共同特征是什么
你能仿照上面的叙述,说明③也是具有确定顺序的一列数吗
知新探究
数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示,第二个位置上的数叫做这个数列的第2项,用a2表示……第n个位置上的数叫做这个数列的第n项,用an表示.其中第1项也叫做首项.
前面研究的例子中,①是按年龄从小到大的顺序排列的,②是照每月的日期从小到大的顺序排列的,③是按幂指数从小到大的顺序排列的,它们都是从第1项开始的.
数列中的每一个数叫做这个数列的项.
注意:这里要理清“数列的项”、“首项”、“数列的项数”.
一般地,我们把按照确定的顺序排列的一列数称为数列(sequence of number).
项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列.
试以①②③例说明它们的“项”、“首项”、“项数”,并判断它们是有穷数列还是无穷数列.
知新探究
数列的一般形式是
a1,a2,a3,…,an,…
简记为{an}.
问题1 1,3,5,7是一个数列,7,5,3,1也是一个数列,这两个数列是不是同一个数列?
问题2 1,1,1,1,1,…是不是一个数列?
问题3:数列与集合有什么区别?
数列{an}中的数是有一定顺序的,而集合中的元素没有顺序;
数列{an}中是一列数,而集合中的元素不一定是数;
数列{an}中的数可以重复,而集合中的元素不能重复.
问题4 {an} 与an的意思一样吗?
知新探究
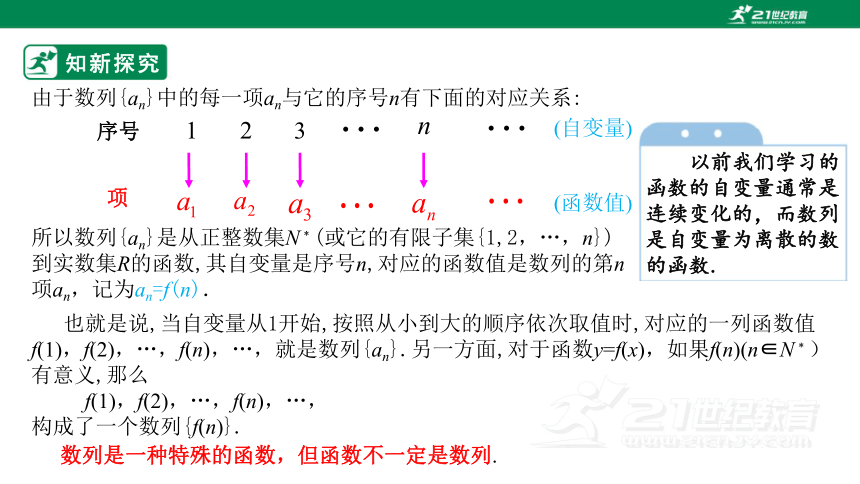
由于数列{an}中的每一项an与它的序号n有下面的对应关系:
所以数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
也就是说,当自变量从1开始,按照从小到大的顺序依次取值时,对应的一列函数值f(1),f(2),…,f(n),…,就是数列{an}.另一方面,对于函数y=f(x),如果f(n)(n∈N﹡)有意义,那么
f(1),f(2),…,f(n),…,
构成了一个数列{f(n)}.
数列是一种特殊的函数,但函数不一定是数列.
序号
项
(自变量)
(函数值)
以前我们学习的 函数的自变量通常是 连续变化的,而数列是自变量为离散的数的函数.
知新探究
与其他函数一样,数列也可以用表格和图象表示
如问题1中的数列①可以表示下表
它的图象如图所示.
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
an 75 87 96 103 110 116 120 128 138 145 153 158 160 162 163 165 168
从上表和上图,你能发现此数列中的项随序号的变化呈现出的特点吗
可以发现数列中的项的大小随序号的增大而增大.
知新探究
从第2项起,每一项都大于它的前一项的数列叫做递增数列;
与函数类似,我们可以定义数列的单调性.
从第2项起,每一项都小于它的前一项的数列叫做递减数列.
特别地,各项都相等的数列叫做常数列.
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫摆动数列.
此数列的通项公式为:an=.
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
例如, 的1次幂、2次幂、3次幂、4次幂……依次排成一列数:
显然,通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
知新探究
【例1】根据下列数列{an}的通项公式, 写出数列的前5项,并画出它们的图象.
⑴; ⑵.
解:
⑴当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,3,6,10,15.
图象如图所示.
知新探究
【例1】根据下列数列{an}的通项公式, 写出数列的前5项,并画出它们的图象.
⑴; ⑵.
解:
⑵当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,0,-1,0,1.
图象如图所示.
思考:数列的图像可能是连续的线条吗?为什么?
初试身手
1.已知数列的通项公式an=,则a2a3等于( )
A.70 B.28 C.20 D.8
解:
由an=,得
∴a2a3=2×10=20.故选C.
C
a2=2×2-2=2,a3=3×3+1=10,
知新探究
【例2】根据下列数列的前4项,写出数列的一个通项公式:
⑴1,1,1,1,…; ⑵1,-1,1,-1,…;
⑶1×2,2×3,3×4,4×5,…; ⑷9,99,999,9999,…;
解:
⑴an=1;
⑵an=(-1)n+1;
an=
⑶an=n(n+1);
⑷an=10n-1;
第⑵题的通项公式还有没有其它结果?
(-1)n或(-1)n+1
常常用来表示正负相间的变化规律.
an=
知新探究
【例2】根据下列数列的前4项,写出数列的一个通项公式:
⑸1,-,… ⑹2,0,2,0,…
解:
⑹可以看成数列1,1,1,1,…与数列1,-1,1,-1,…,对应项的和所得的数列,an=1+(-1)n+1.
这两道题的通项公式还有没有其它结果?
⑹an=1+(-1)n+1.
⑸;
分析:⑸可以看成数列1,,…与数列1,-1,1,-1,…,对应项的乘积所得的数列,;
注意:
①一些数列的通项公式不是唯一的;
②不是每一个数列都能写出它的通项公式;
③常用来表示正负相间的变化规律.
知新探究
用观察法求数列通项公式的策略
1.统一数列各项的表示形式;
2.根据数列各项的结构拆项,使每一部分与项数的关系更明显;
3.根据每一部分与项数的关系,写出数列的通项公式.
初试身手
⑴an=2n-1;
⑵an=;
2.根据下列数列的前4项,写出数列的一个通项公式:
⑴ 1,3,5,7,…; ⑵ 1,11,111,1111,…;
⑶0.9,0.99,0.999,0.9999,…; ⑷ ,…;
⑸,…; ⑹,….
⑶an=1-;
⑷an= ;
解:
⑸an=;
⑹an=.
课堂小结
1.数列
把按照确定的顺序排列的一列数称为数列(sequence of number).数列中的每一个数叫做这个数列的项.
2.数列的分类
数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
类别 含义
按项数
按项的变化趋势
有穷数列
无穷数列
项数有限的数列叫做有穷数列
项数无限的数列叫做有穷数列
递增数列
从第2项起,每一项都大于它的前一项的数列叫做递增数列
递减数列
从第2项起,每一项都小于它的前一项的数列叫做递减数列
常数列
各项都相等的数列叫做常数列
摆动数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫做摆动数列
课堂小结
3.数列的表示
①按顺序一一列举:a1,a2,a3,…,an,… 简记{an}
②列表法
③图象法
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
④通项公式法
作业布置
作业: P5 练习 第2,3题
P8 习题4.1 第1,2⑴⑵,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第四章 数列
4.1 数列的概念(第1课时)
教学目标
学习目标 数学素养
1.理解数列的有关概念与数列的表示方法. 1.逻辑推理素养.
2.掌握数列的分类,了解数列的单调性. 2.数学抽象素养.
3.理解数列的通项公式,并会用通项公式写出数列的任一项. 3.逻辑推理素养和数学运算素养.
本章引入
第四章 数列
对数列的研究源于现实生产、生活的需要. 例如,一棵树在某一时刻的高度是2m,如果在每年的同-时刻都记录下这棵树的高度,并按先后顺序排列起来,就得到一列数.人们常用这样的一列数有序地表达一类事物,或者记录一个过程.像这样按照确定的顺序排列的一列数称为数列.如果用正整数表示事物发展过程的先后顺序,并且把这样的正整数看作自变量的取值,把事物的对应数值看作相应的函数值,那么数列就是定义在正整数集(或正整数集的有限子集)上的一类离散函数.
本章我们将学习数列的概念和表示方法,并研究两类特殊的数列——等差数列和等比数列,探索它们的取值规律,建立它们的通项公式、前n项和公式,并应用它们解决一些问题. 我们将把数列看成一类特殊的函数,并用函数的思想方法研究数列. 我们还将学习数学归纳法,这是一种证明与正整数有关的数学命题的特殊方法.在本章的学习中,我们可以体验通过数学抽象获得一个数学对象,并通过数学运算、逻辑推理等进行研究的过程和方法;通过建立数学模型刻画具有递推规律的事物,提高解决实际问题的能力.
新知探究
4.1 的概念(第1课时)
在现实生活和数学学习中,我们经常需要根据问题的意义,通过对一些数据按特定顺序排列的方法来刻画研究对象.例如:
1.王芳从1岁到17岁,每年生日那天测量身高,将这些身高数据(单位:cm)依次排成一列数:
75,87,96,103,110,116,120,128,138,
145,153,158,160,162,163,165,168. ①
记王芳第i岁时的身高为hi,
那么h1=75,h2=87,……,h17=168.
我们发现,hi 中的i反映了身高按岁数从1到17的顺序排列时的确定位置,h1=75是排在第一位的数,h2=87是排在第二位的数,……,h17 =168是排在第17位的数,
它们之间不能交换位置.
所以,①是具有确定顺序的一列数.
知新引入
记第i天月亮可见部分的数为si,那么s1=5,s2=10,…,s15=240. 这里,si中的i反映了月亮可见部分的数按日期从1到15的顺序排列时的确定位置,即s1=5是排在第1位的数,s2=10是排在第2位的数,…,s15=240是排在第15位的数,
2. 在两河流域发掘的一块泥版上就有一列依次表示一个月中从第1天到第15天每天月亮可见部分的数:
5,10,20,40,80,96,112,128,
144,160,176,192,208,224,240 ②
把满月分成240份,则从初一到十五每天月亮的可见部分可用一个代表份数的数来表示.
它们之间不能交换位置.
所以,②也是具有确定顺序的一列数.
知新探究
- -,… ③
记i次幂为ai ,那么a1 =- ,a2 = ,…,这里ai 中的i反映了从1到n按顺序排列时的确定位置,a1 =-是排第一位的数,a2= 是排在第二位的数,…
3.的n次幂按1次幂、2次幂、3次幂、4次幂……依次排成一列数:
.
它们之间不能交换位置.
所以,③也是具有确定顺序的一列数.
上述例子的共同特征是什么
你能仿照上面的叙述,说明③也是具有确定顺序的一列数吗
知新探究
数列的第一个位置上的数叫做这个数列的第1项,常用符号a1表示,第二个位置上的数叫做这个数列的第2项,用a2表示……第n个位置上的数叫做这个数列的第n项,用an表示.其中第1项也叫做首项.
前面研究的例子中,①是按年龄从小到大的顺序排列的,②是照每月的日期从小到大的顺序排列的,③是按幂指数从小到大的顺序排列的,它们都是从第1项开始的.
数列中的每一个数叫做这个数列的项.
注意:这里要理清“数列的项”、“首项”、“数列的项数”.
一般地,我们把按照确定的顺序排列的一列数称为数列(sequence of number).
项数有限的数列叫做有穷数列,项数无限的数列叫做无穷数列.
试以①②③例说明它们的“项”、“首项”、“项数”,并判断它们是有穷数列还是无穷数列.
知新探究
数列的一般形式是
a1,a2,a3,…,an,…
简记为{an}.
问题1 1,3,5,7是一个数列,7,5,3,1也是一个数列,这两个数列是不是同一个数列?
问题2 1,1,1,1,1,…是不是一个数列?
问题3:数列与集合有什么区别?
数列{an}中的数是有一定顺序的,而集合中的元素没有顺序;
数列{an}中是一列数,而集合中的元素不一定是数;
数列{an}中的数可以重复,而集合中的元素不能重复.
问题4 {an} 与an的意思一样吗?
知新探究
由于数列{an}中的每一项an与它的序号n有下面的对应关系:
所以数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
也就是说,当自变量从1开始,按照从小到大的顺序依次取值时,对应的一列函数值f(1),f(2),…,f(n),…,就是数列{an}.另一方面,对于函数y=f(x),如果f(n)(n∈N﹡)有意义,那么
f(1),f(2),…,f(n),…,
构成了一个数列{f(n)}.
数列是一种特殊的函数,但函数不一定是数列.
序号
项
(自变量)
(函数值)
以前我们学习的 函数的自变量通常是 连续变化的,而数列是自变量为离散的数的函数.
知新探究
与其他函数一样,数列也可以用表格和图象表示
如问题1中的数列①可以表示下表
它的图象如图所示.
n 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
an 75 87 96 103 110 116 120 128 138 145 153 158 160 162 163 165 168
从上表和上图,你能发现此数列中的项随序号的变化呈现出的特点吗
可以发现数列中的项的大小随序号的增大而增大.
知新探究
从第2项起,每一项都大于它的前一项的数列叫做递增数列;
与函数类似,我们可以定义数列的单调性.
从第2项起,每一项都小于它的前一项的数列叫做递减数列.
特别地,各项都相等的数列叫做常数列.
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫摆动数列.
此数列的通项公式为:an=.
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
例如, 的1次幂、2次幂、3次幂、4次幂……依次排成一列数:
显然,通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
知新探究
【例1】根据下列数列{an}的通项公式, 写出数列的前5项,并画出它们的图象.
⑴; ⑵.
解:
⑴当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,3,6,10,15.
图象如图所示.
知新探究
【例1】根据下列数列{an}的通项公式, 写出数列的前5项,并画出它们的图象.
⑴; ⑵.
解:
⑵当通项公式中的n=1,2,3,4,5时,数列{an}的前5项依次为1,0,-1,0,1.
图象如图所示.
思考:数列的图像可能是连续的线条吗?为什么?
初试身手
1.已知数列的通项公式an=,则a2a3等于( )
A.70 B.28 C.20 D.8
解:
由an=,得
∴a2a3=2×10=20.故选C.
C
a2=2×2-2=2,a3=3×3+1=10,
知新探究
【例2】根据下列数列的前4项,写出数列的一个通项公式:
⑴1,1,1,1,…; ⑵1,-1,1,-1,…;
⑶1×2,2×3,3×4,4×5,…; ⑷9,99,999,9999,…;
解:
⑴an=1;
⑵an=(-1)n+1;
an=
⑶an=n(n+1);
⑷an=10n-1;
第⑵题的通项公式还有没有其它结果?
(-1)n或(-1)n+1
常常用来表示正负相间的变化规律.
an=
知新探究
【例2】根据下列数列的前4项,写出数列的一个通项公式:
⑸1,-,… ⑹2,0,2,0,…
解:
⑹可以看成数列1,1,1,1,…与数列1,-1,1,-1,…,对应项的和所得的数列,an=1+(-1)n+1.
这两道题的通项公式还有没有其它结果?
⑹an=1+(-1)n+1.
⑸;
分析:⑸可以看成数列1,,…与数列1,-1,1,-1,…,对应项的乘积所得的数列,;
注意:
①一些数列的通项公式不是唯一的;
②不是每一个数列都能写出它的通项公式;
③常用来表示正负相间的变化规律.
知新探究
用观察法求数列通项公式的策略
1.统一数列各项的表示形式;
2.根据数列各项的结构拆项,使每一部分与项数的关系更明显;
3.根据每一部分与项数的关系,写出数列的通项公式.
初试身手
⑴an=2n-1;
⑵an=;
2.根据下列数列的前4项,写出数列的一个通项公式:
⑴ 1,3,5,7,…; ⑵ 1,11,111,1111,…;
⑶0.9,0.99,0.999,0.9999,…; ⑷ ,…;
⑸,…; ⑹,….
⑶an=1-;
⑷an= ;
解:
⑸an=;
⑹an=.
课堂小结
1.数列
把按照确定的顺序排列的一列数称为数列(sequence of number).数列中的每一个数叫做这个数列的项.
2.数列的分类
数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
类别 含义
按项数
按项的变化趋势
有穷数列
无穷数列
项数有限的数列叫做有穷数列
项数无限的数列叫做有穷数列
递增数列
从第2项起,每一项都大于它的前一项的数列叫做递增数列
递减数列
从第2项起,每一项都小于它的前一项的数列叫做递减数列
常数列
各项都相等的数列叫做常数列
摆动数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫做摆动数列
课堂小结
3.数列的表示
①按顺序一一列举:a1,a2,a3,…,an,… 简记{an}
②列表法
③图象法
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
④通项公式法
作业布置
作业: P5 练习 第2,3题
P8 习题4.1 第1,2⑴⑵,3题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
