2024-2025学年八年级上学期第一次月考数学试卷(北师大版)(考查范围:第1章~第2章第5节)(无答案)
文档属性
| 名称 | 2024-2025学年八年级上学期第一次月考数学试卷(北师大版)(考查范围:第1章~第2章第5节)(无答案) |  | |
| 格式 | doc | ||
| 文件大小 | 304.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 08:43:40 | ||
图片预览


文档简介
2024-2025学年八年级上学期第一次月考数学试卷
(考查范围:第1章~第2章第5节)
(时间:120分钟 满分:150分)
一.选择题(每小题3分,共36分.每小题均有A,B,C,D四个选项,其中只有一个选项正确)
1.下列各组数中,是“勾股数”的一组是( )
A.4,5,6 B.1.5,2,2.5
C.6,8,10 D.0.3,0.4,0.5
2.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
3.下列各组数中,以a,b,c为边长的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=9,b=40,c=41
4.已知2a+1和7是正数b的两个平方根,则a的值是( )
A.3 B.49 C.4 D.﹣4
5.如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A. B. C. D.2
6.如图,点B在正方形ADEC的内部,连接AB,AC,若∠CBA=90°,AB=1,BC=,则正方形ADEC的面积是( )
A.3 B.4 C.5 D.6
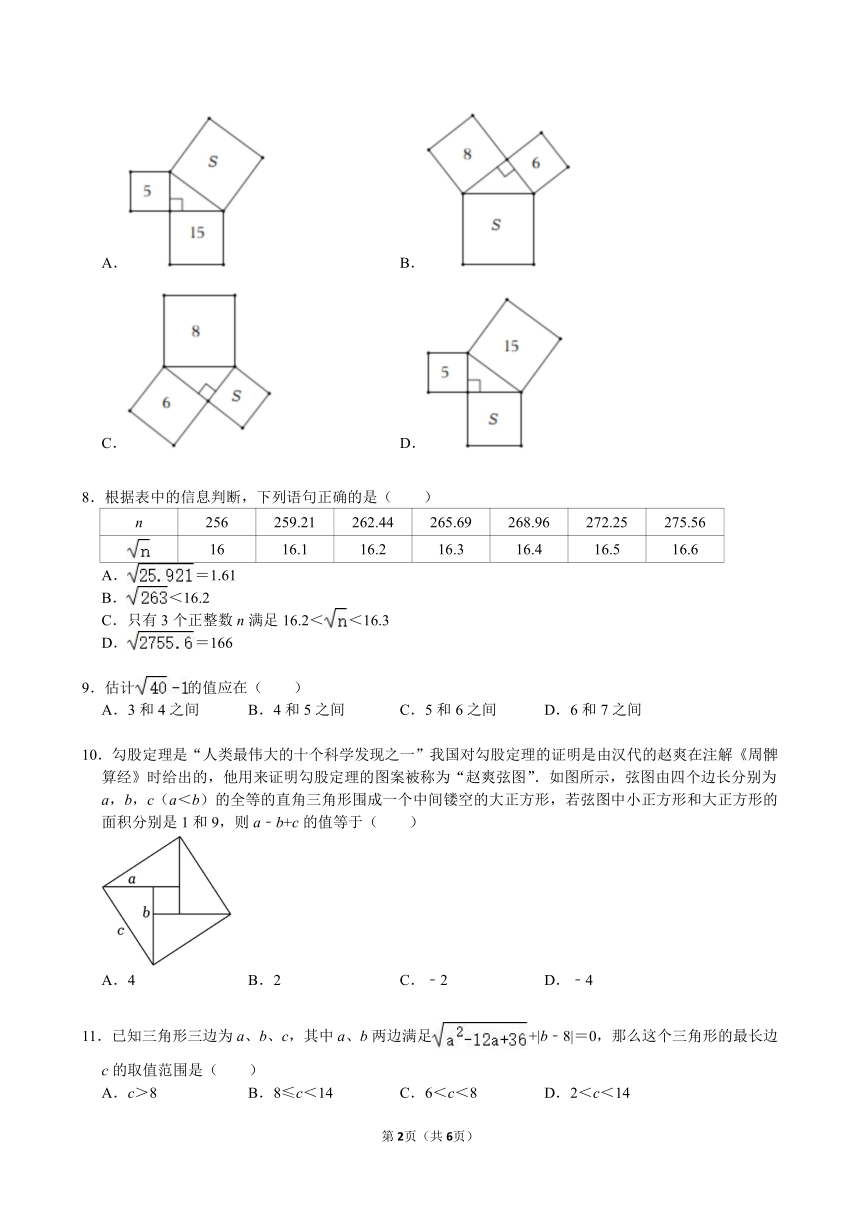
7.下列各图是以直角三角形各边为边,在三角形外部画正方形得到的,每个正方形中的数及字母S表示所在正方形的面积.其中S的值恰好等于10的是( )
A. B.
C. D.
8.根据表中的信息判断,下列语句正确的是( )
n 256 259.21 262.44 265.69 268.96 272.25 275.56
16 16.1 16.2 16.3 16.4 16.5 16.6
A.=1.61
B.<16.2
C.只有3个正整数n满足16.2<<16.3
D.=166
9.估计的值应在( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
10.勾股定理是“人类最伟大的十个科学发现之一”我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.如图所示,弦图由四个边长分别为a,b,c(a<b)的全等的直角三角形围成一个中间镂空的大正方形,若弦图中小正方形和大正方形的面积分别是1和9,则a﹣b+c的值等于( )
A.4 B.2 C.﹣2 D.﹣4
11.已知三角形三边为a、b、c,其中a、b两边满足+|b﹣8|=0,那么这个三角形的最长边c的取值范围是( )
A.c>8 B.8≤c<14 C.6<c<8 D.2<c<14
12.将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
二.填空题(每小题4分,共16分)
13.25的算术平方根是 ;的立方根是 .
14.一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是 .
15.在Rt△ABC中,,则AB= .
16.若,则整数x的最小值为 .
三.解答题(本大题共9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)求下列各式x的值.
(1)4(x+1)2=81;
(2)27(x﹣2)3﹣8=0.
18.(9分)设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
19.(10分)用2个完全一样的等腰直角三角形可以拼成一个正方形,用4个完全一样的等腰直角三角形也可以拼成一个正方形.(见图)
如果这个等腰直角三角形的斜边长是10厘米,请你利用上面的知识计算这个等腰直角三角形的面积.
20.(11分)已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是的整数部分.
(1)求a、b、c的值;
(2)求a+2b﹣c+2的算术平方根.
21.(10分)如图,已知CD⊥AB,垂足为D,BD=1,CD=2,AD=4,判断△ABC的形状,并说明理由.
22.某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:
测量示意图
测量数据 边的长度 ①测得水平距离BC的长为15米.
②根据手中剩余线的长度计算出了风筝拉线AB的长为17米.
③小明牵线放风筝的手到地面的距离为1.7米.
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度AD.请完成以下任务:
(1)根据上述信息,求风筝离地面的垂直高度AD.
(2)如果小明想要风筝沿DA方向再上升12米,BC长度不变,则他应该再放出多少米风筝拉线?
23.(12分)如图,是一块体积为216立方厘米的立方体铁块.
(1)求出这个铁块的棱长.
(2)现在工厂要将这个铁块融化,重新锻造成两个棱长为2厘米的小立方体铁块和一个底面为正方形的长方体铁块,若长方体铁块的高为8厘米,求长方体铁块的底面正方形的边长.
24.(12分)数与形是数学中的两个最古老,也是最基本的研究对象.数与形也是有联系的,这种联系称为“数形结合”.利用“数形结合”思想可以直观地帮助我们解决一些数学验证或运算.
(1)我国是最早了解勾股定理的国家之一,该定理阐明了直角三角形的三边关系.请你利用如图对勾股定理(即下列命题)进行验证,从中体会“数形结合”的思想:
已知:如图,在Rt△ABC和Rt△CDE中,∠B=∠D=∠ACE=90°,(点B,C,D在一条直线上),AB=b,BC=a,AC=EC=c.
证明:a2+b2=c2;
(2)请利用“数形结合”思想,画图推算出(a+b+c)2的结果.
25.(12分)小明制作了一张边长为16cm的正方形贺卡想寄给朋友,现有一个面积为426cm2的长方形信封如图所示,信封长和宽的比为3:2.
(1)求此长方形信封的长和宽;
(2)小明能将这张贺卡不折叠就放入此信封吗?请通过计算说明理由.
第6页(共13页)
(考查范围:第1章~第2章第5节)
(时间:120分钟 满分:150分)
一.选择题(每小题3分,共36分.每小题均有A,B,C,D四个选项,其中只有一个选项正确)
1.下列各组数中,是“勾股数”的一组是( )
A.4,5,6 B.1.5,2,2.5
C.6,8,10 D.0.3,0.4,0.5
2.的算术平方根等于( )
A.4 B.±4 C.2 D.±2
3.下列各组数中,以a,b,c为边长的三角形不是直角三角形的是( )
A.a=1.5,b=2,c=3 B.a=7,b=24,c=25
C.a=6,b=8,c=10 D.a=9,b=40,c=41
4.已知2a+1和7是正数b的两个平方根,则a的值是( )
A.3 B.49 C.4 D.﹣4
5.如图,一只蚂蚁从棱长为1的正方体纸箱的A点沿纸箱表面爬到B点,那么它所爬行的最短路线的长是( )
A. B. C. D.2
6.如图,点B在正方形ADEC的内部,连接AB,AC,若∠CBA=90°,AB=1,BC=,则正方形ADEC的面积是( )
A.3 B.4 C.5 D.6
7.下列各图是以直角三角形各边为边,在三角形外部画正方形得到的,每个正方形中的数及字母S表示所在正方形的面积.其中S的值恰好等于10的是( )
A. B.
C. D.
8.根据表中的信息判断,下列语句正确的是( )
n 256 259.21 262.44 265.69 268.96 272.25 275.56
16 16.1 16.2 16.3 16.4 16.5 16.6
A.=1.61
B.<16.2
C.只有3个正整数n满足16.2<<16.3
D.=166
9.估计的值应在( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
10.勾股定理是“人类最伟大的十个科学发现之一”我国对勾股定理的证明是由汉代的赵爽在注解《周髀算经》时给出的,他用来证明勾股定理的图案被称为“赵爽弦图”.如图所示,弦图由四个边长分别为a,b,c(a<b)的全等的直角三角形围成一个中间镂空的大正方形,若弦图中小正方形和大正方形的面积分别是1和9,则a﹣b+c的值等于( )
A.4 B.2 C.﹣2 D.﹣4
11.已知三角形三边为a、b、c,其中a、b两边满足+|b﹣8|=0,那么这个三角形的最长边c的取值范围是( )
A.c>8 B.8≤c<14 C.6<c<8 D.2<c<14
12.将一组数,2,,2,,2,…,,…,按以下方式进行排列:则第八行左起第1个数是( )
A.7 B.8 C. D.4
二.填空题(每小题4分,共16分)
13.25的算术平方根是 ;的立方根是 .
14.一个三角形的三边长之比是5:12:13,且周长是60,则它的面积是 .
15.在Rt△ABC中,,则AB= .
16.若,则整数x的最小值为 .
三.解答题(本大题共9小题,共98分.解答应写出必要的文字说明、证明过程或演算步骤)
17.(10分)求下列各式x的值.
(1)4(x+1)2=81;
(2)27(x﹣2)3﹣8=0.
18.(9分)设直角三角形的两条直角边长分别为a和b,斜边长为c.
(1)已知a=6,c=10,求b;
(2)已知a=5,b=12,求c;
(3)已知c=25,b=15,求a.
19.(10分)用2个完全一样的等腰直角三角形可以拼成一个正方形,用4个完全一样的等腰直角三角形也可以拼成一个正方形.(见图)
如果这个等腰直角三角形的斜边长是10厘米,请你利用上面的知识计算这个等腰直角三角形的面积.
20.(11分)已知2a﹣1的平方根是±3,3a+b﹣9的立方根是2,c是的整数部分.
(1)求a、b、c的值;
(2)求a+2b﹣c+2的算术平方根.
21.(10分)如图,已知CD⊥AB,垂足为D,BD=1,CD=2,AD=4,判断△ABC的形状,并说明理由.
22.某实践探究小组在放风筝时想测量风筝离地面的垂直高度,通过勘测,得到如下记录表:
测量示意图
测量数据 边的长度 ①测得水平距离BC的长为15米.
②根据手中剩余线的长度计算出了风筝拉线AB的长为17米.
③小明牵线放风筝的手到地面的距离为1.7米.
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度AD.请完成以下任务:
(1)根据上述信息,求风筝离地面的垂直高度AD.
(2)如果小明想要风筝沿DA方向再上升12米,BC长度不变,则他应该再放出多少米风筝拉线?
23.(12分)如图,是一块体积为216立方厘米的立方体铁块.
(1)求出这个铁块的棱长.
(2)现在工厂要将这个铁块融化,重新锻造成两个棱长为2厘米的小立方体铁块和一个底面为正方形的长方体铁块,若长方体铁块的高为8厘米,求长方体铁块的底面正方形的边长.
24.(12分)数与形是数学中的两个最古老,也是最基本的研究对象.数与形也是有联系的,这种联系称为“数形结合”.利用“数形结合”思想可以直观地帮助我们解决一些数学验证或运算.
(1)我国是最早了解勾股定理的国家之一,该定理阐明了直角三角形的三边关系.请你利用如图对勾股定理(即下列命题)进行验证,从中体会“数形结合”的思想:
已知:如图,在Rt△ABC和Rt△CDE中,∠B=∠D=∠ACE=90°,(点B,C,D在一条直线上),AB=b,BC=a,AC=EC=c.
证明:a2+b2=c2;
(2)请利用“数形结合”思想,画图推算出(a+b+c)2的结果.
25.(12分)小明制作了一张边长为16cm的正方形贺卡想寄给朋友,现有一个面积为426cm2的长方形信封如图所示,信封长和宽的比为3:2.
(1)求此长方形信封的长和宽;
(2)小明能将这张贺卡不折叠就放入此信封吗?请通过计算说明理由.
第6页(共13页)
同课章节目录
