28.2.2解直角三角形应用举例(1)课件
文档属性
| 名称 | 28.2.2解直角三角形应用举例(1)课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 302.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 13:56:05 | ||
图片预览



文档简介
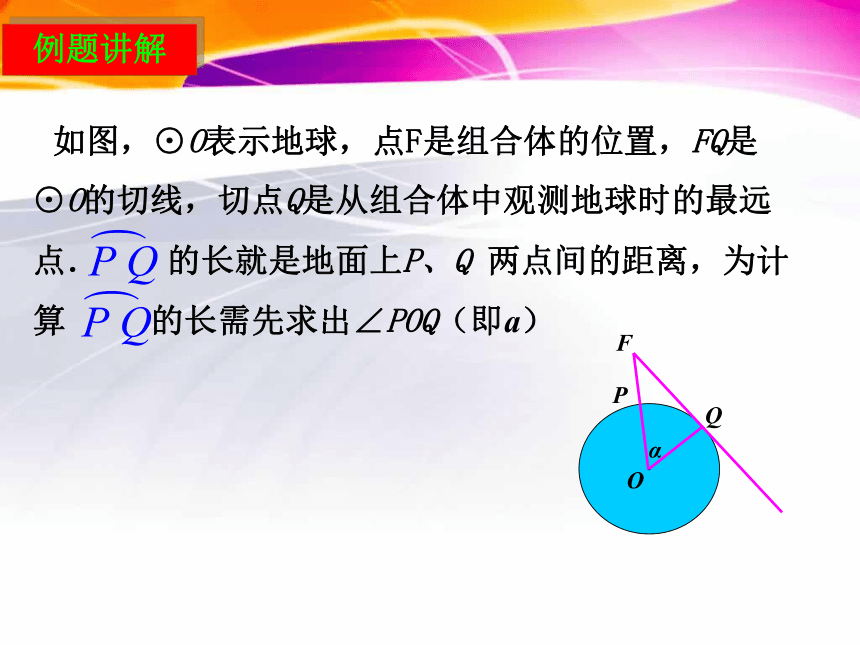
课件13张PPT。 28.2.2应用举例(1)例3: 2012年6月18日“神舟”九号载人航天飞船与“天宫”一号目标飞行成功实现交会对接。“神舟”九号与“天宫”一号的组合就在离地球表面343km的圆形轨道上运行.如图,当组合体运行到地球表面P点的正上方时,从中能直接看到地球上的点在什么位置?这样的最远点与P点的距离是多少?(地球半径约为6 400km,圆周率取3.142,结果取整数) 分析:从飞船上能最远直接看到的地球上的点,应是视线与地球相切时的切点.例题讲解 如图,⊙O表示地球,点F是组合体的位置,FQ是⊙O的切线,切点Q是从组合体中观测地球时的最远点. 的长就是地面上P、Q 两点间的距离,为计算 的长需先求出∠POQ(即a)例题讲解 解:在图中,FQ是⊙O的切线,△FOQ是直角三角形.∴ PQ的长为 当飞船在P点正上方时,从飞船观测地球时的最远点距离P点约2051km例题讲解 仰角和俯角垂直线水平线视线视线仰角俯角在进行测量时,
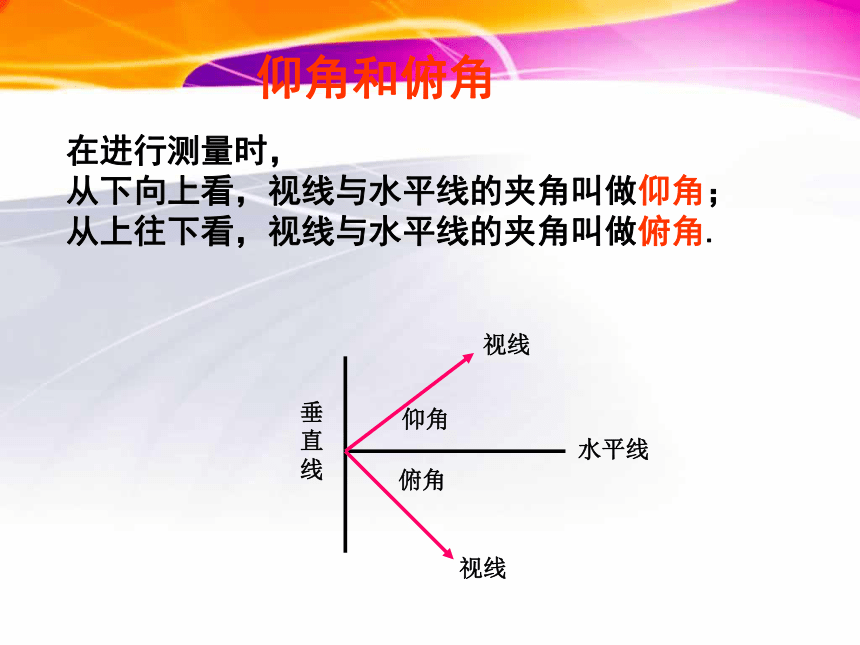
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
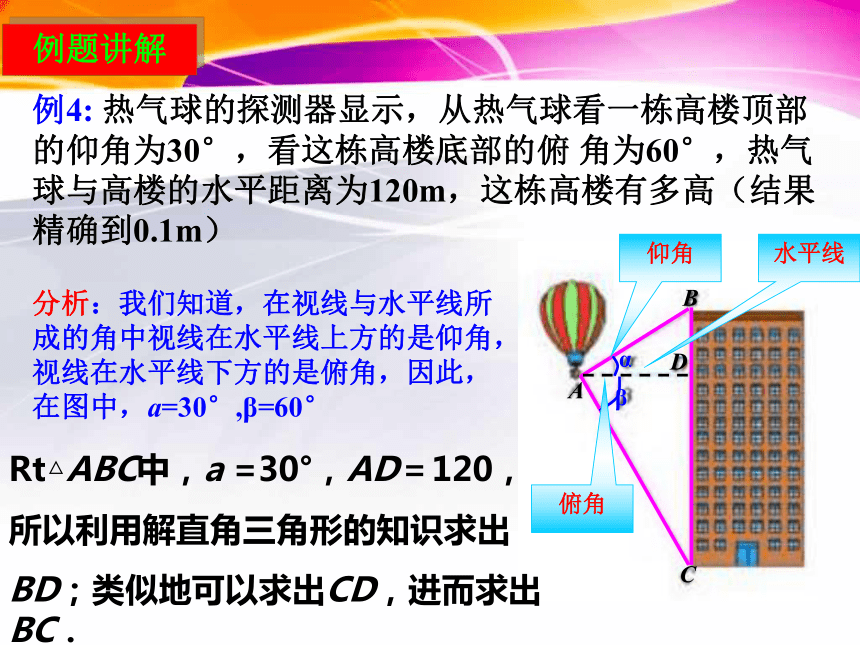
例4: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.仰角水平线俯角例题讲解 解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m.1. 建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)解:在等腰三角形BCD中∠ACD=90°BC=DC=40m在Rt△ACD中所以AB=AC-BC=55.2-40=15.2答:棋杆的高度为15.2m.课内练习 2. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远正好能使A,C,E成一直线(精确到0.1m)∴∠BED=∠ABD-∠D=90°答:开挖点E离点D 332.8m正好能使A,C,E成一直线.解:要使A、C、E在同一直线上,则 ∠ABD是 △BDE 的一个外角课内练习 感悟:利用解直角三角形的知识解决实际问题
的一般步骤:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.(有“弦”用“弦”; 无“弦”用“切”)2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为 (根号保留). 作业布置:
第78页 3. 4题
从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
例4: 热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m)分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°Rt△ABC中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.仰角水平线俯角例题讲解 解:如图,a = 30°,β= 60°, AD=120.答:这栋楼高约为277.1m.1. 建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角50°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m)解:在等腰三角形BCD中∠ACD=90°BC=DC=40m在Rt△ACD中所以AB=AC-BC=55.2-40=15.2答:棋杆的高度为15.2m.课内练习 2. 如图,沿AC方向开山修路.为了加快施工进度,要在小山的另一边同时施工,从AC上的一点B取∠ABD = 140°,BD = 520m,∠D=50°,那么开挖点E离D多远正好能使A,C,E成一直线(精确到0.1m)∴∠BED=∠ABD-∠D=90°答:开挖点E离点D 332.8m正好能使A,C,E成一直线.解:要使A、C、E在同一直线上,则 ∠ABD是 △BDE 的一个外角课内练习 感悟:利用解直角三角形的知识解决实际问题
的一般步骤:1.将实际问题抽象为数学问题;(画出平面图形,转化为解直角三角形的问题)2.根据条件的特点,适当选用锐角三角函数等
去解直角三角形;3.得到数学问题的答案;4.得到实际问题的答案.(有“弦”用“弦”; 无“弦”用“切”)2.如图2,在离铁塔BE 120m的A处,用测角仪测量塔顶的仰角为30°,已知测角仪高AD=1.5m,则塔高BE= _________ (根号保留).1.如图1,已知楼房AB高为50m,铁塔塔基距楼房地基间的水平距离BD为100m,塔高CD为 m,则下面结论中正确的是( )
A.由楼顶望塔顶仰角为60°
B.由楼顶望塔基俯角为60°
C.由楼顶望塔顶仰角为30°
D.由楼顶望塔基俯角为30°C3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200m,点C在BD上,则树高AB等于 (根号保留).4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°
,则折叠后重叠部分的面积为 (根号保留). 作业布置:
第78页 3. 4题
