第21-23章期中章节巩固训练(无答案)2024-2025学年 人教版数学九年级上册
文档属性
| 名称 | 第21-23章期中章节巩固训练(无答案)2024-2025学年 人教版数学九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 357.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 00:00:00 | ||
图片预览


文档简介
第21-23章期中章节巩固训练2024-2025年度人教版九年级上册
板块一:一元二次方程
1.一元二次方程(4x+1)(2x﹣3)=5x2+1化成一般式后a,b,c的值为( )
A.3,﹣10,﹣4 B.3,﹣12,﹣2 C.8,﹣10,﹣2 D.8,﹣12,4
2.一元二次方程配方后可变形为( )
A. B. C. D.
3.若关于x的一元二次方程ax2+bx+1=0的一个解是x=1,则2021+a+b=( )
A.2020 B.2021 C.2022 D.2023
4.已知一元二次方程x2-4x-2=0的两根分别为x1,x2,则的值为( )
A.2 B.-1 C. D.-2
5.三角形两边长分别为2和3,第三边的长是方程2x2﹣13x+15=0的根,则该三角形的周长为( )
A. B.10 C. D.或10
6.已知关于x的一元二次方程mx2﹣3x+1=0有两个实数根,则m的取值范围是 .
7.已知代数式7x(x+5)+10与代数式9x﹣9的值相等,则x= .
8.某种树木的主干长出根枝干,每个枝干又长出根小分支,若主干、枝干和小分支总数共根,则主干长出枝干的根数为______.
9. 用适当的方法解下列方程
(1)3y(y+1)=y+1; (2)x2+4x﹣1=0.
10.已知关于x的一元二次方程(a+c)x2﹣2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果△ABC是等边三角形,试求这个一元二次方程的根.
板块二:二次函数
1.下列对抛物线性质的描写中,正确的是( )
A.开口向上 B.对称轴是直线x=9
C.顶点坐标是(﹣4,9) D.函数y有最大值
2.已知点,都在函数的图象上,则与大小关系正确的是( )
A. B. C. D.
3.把抛物线向左平移3个单位,再向下平移2个单位,所得抛物线的顶点坐标是( )
A.(5,) B.(5,0) C.(,) D.(,0)
4. 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=-(x-3)2C.y=-(x+3)2 D.y=(x-3)2
5.二次函数y=﹣3x2+5x+1的图象开口方向 ;对称轴为 .
6.无论取任何实数,抛物线的顶点一定不在__________象限.
7.矩形的边长分别为和,若每边长都增加,则面积增加,则与的函数关系式为________.
8.如图,点A(0,1),平行于x轴的直线AC分别交抛物线与(x≥0)于B、C两点,过点C作y轴的平行线交于点D,直线DE∥AC,交于点E,则DE=________.
9.为落实国家精准扶贫政策,某地扶贫办决定帮助扶贫对象推销当地特色农产品,该农产品成本价为18元每千克,销售单价y(元)与每天销售量x(千克)(x为正整数)之间满足如图所示的函数关系,其中销售单价不得低于成本价.
(1)求出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)当销售量为多少时,获利最大?最大利润是多少?
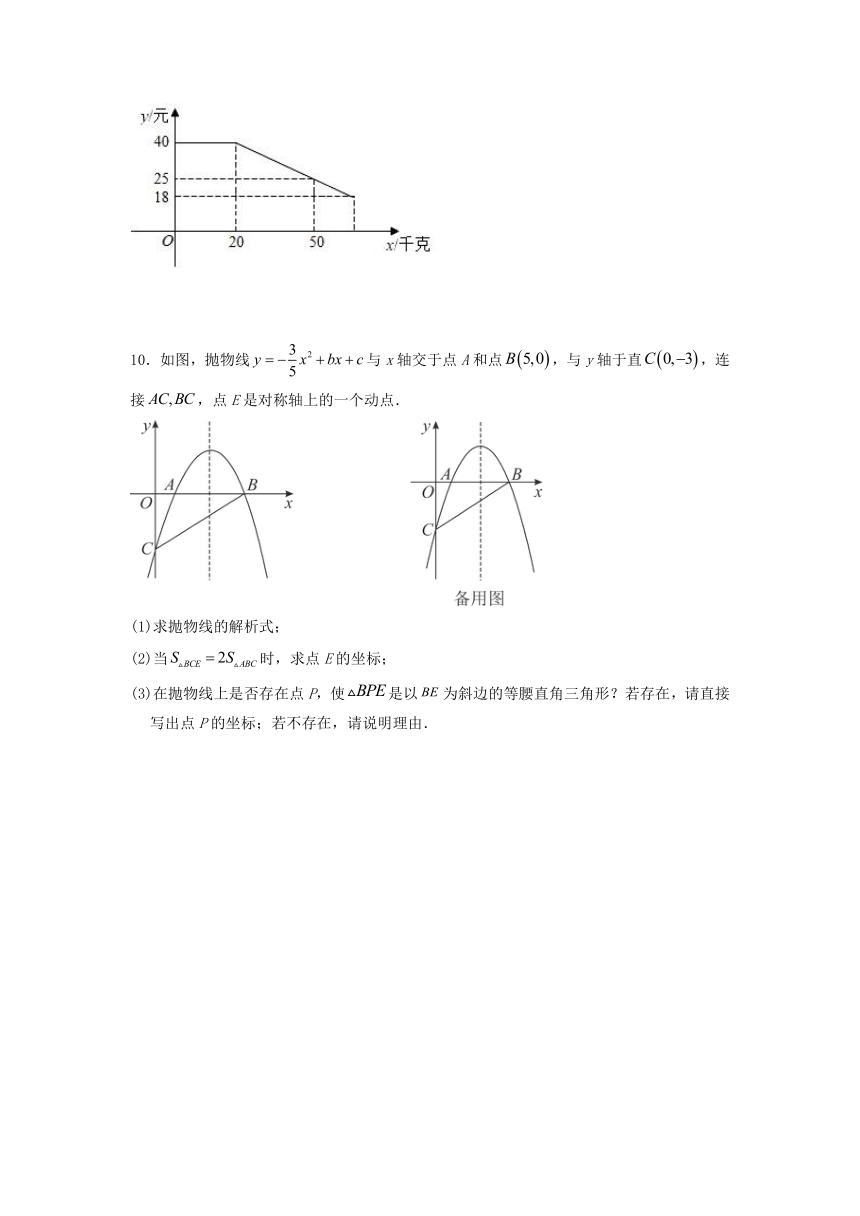
10.如图,抛物线与x轴交于点A和点,与y轴于直,连接,点E是对称轴上的一个动点.
(1)求抛物线的解析式;
(2)当时,求点E的坐标;
(3)在抛物线上是否存在点P,使是以为斜边的等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
板块三:旋转
1.下列图形中,不是中心对称图形的是( )
A. B.
C. D.
2.在平面直角坐标系xOy中,点M与点N(3,4)关于原点对称,那么点M的坐标为( )
A.(3,4) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
3.如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
4.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
5.如图,已知 中,于点E,以点B为中心,取旋转角等于,把顺时针旋转,得到,连接若,,则的大小为( )
A. B. C. D.
6.如图,以点O为旋转中心,将△ABO按顺时针方向旋转100°得到△DOF,若∠AOB=40°, 则∠DOB为 度.
7.如图,在中,,,,可以由绕点C顺时针旋转得到,其中点与点A是对应点,点与点B是对应点,连接,且A、、在同一条直线上,则的长为 .
8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转后得到正方形,依此方式,绕点O连续旋转2023次得到正方形,如果点A的坐标为,那么点的坐标为______.
9.如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
10.如图,四边形、都是正方形.
(1)如图1,若,,求的长;
(2)如图2,正方形绕点B逆时针旋转,使点G正好落在上,求证:;
(3)如图3,在(2)条件下,,,点M为直线上一动点,连接,过点作,垂足为点,直接写出的最小值为______.
板块一:一元二次方程
1.一元二次方程(4x+1)(2x﹣3)=5x2+1化成一般式后a,b,c的值为( )
A.3,﹣10,﹣4 B.3,﹣12,﹣2 C.8,﹣10,﹣2 D.8,﹣12,4
2.一元二次方程配方后可变形为( )
A. B. C. D.
3.若关于x的一元二次方程ax2+bx+1=0的一个解是x=1,则2021+a+b=( )
A.2020 B.2021 C.2022 D.2023
4.已知一元二次方程x2-4x-2=0的两根分别为x1,x2,则的值为( )
A.2 B.-1 C. D.-2
5.三角形两边长分别为2和3,第三边的长是方程2x2﹣13x+15=0的根,则该三角形的周长为( )
A. B.10 C. D.或10
6.已知关于x的一元二次方程mx2﹣3x+1=0有两个实数根,则m的取值范围是 .
7.已知代数式7x(x+5)+10与代数式9x﹣9的值相等,则x= .
8.某种树木的主干长出根枝干,每个枝干又长出根小分支,若主干、枝干和小分支总数共根,则主干长出枝干的根数为______.
9. 用适当的方法解下列方程
(1)3y(y+1)=y+1; (2)x2+4x﹣1=0.
10.已知关于x的一元二次方程(a+c)x2﹣2bx+(a﹣c)=0,其中a、b、c分别为△ABC三边的长.
(1)如果x=1是方程的根,试判断△ABC的形状,并说明理由;
(2)如果△ABC是等边三角形,试求这个一元二次方程的根.
板块二:二次函数
1.下列对抛物线性质的描写中,正确的是( )
A.开口向上 B.对称轴是直线x=9
C.顶点坐标是(﹣4,9) D.函数y有最大值
2.已知点,都在函数的图象上,则与大小关系正确的是( )
A. B. C. D.
3.把抛物线向左平移3个单位,再向下平移2个单位,所得抛物线的顶点坐标是( )
A.(5,) B.(5,0) C.(,) D.(,0)
4. 为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图),对应的两条抛物线关于y轴对称,AE∥x轴,AB=4 cm,最低点C在x轴上,高CH=1 cm,BD=2 cm.则右轮廓线DFE所在抛物线的函数解析式为( )
A.y=(x+3)2 B.y=-(x-3)2C.y=-(x+3)2 D.y=(x-3)2
5.二次函数y=﹣3x2+5x+1的图象开口方向 ;对称轴为 .
6.无论取任何实数,抛物线的顶点一定不在__________象限.
7.矩形的边长分别为和,若每边长都增加,则面积增加,则与的函数关系式为________.
8.如图,点A(0,1),平行于x轴的直线AC分别交抛物线与(x≥0)于B、C两点,过点C作y轴的平行线交于点D,直线DE∥AC,交于点E,则DE=________.
9.为落实国家精准扶贫政策,某地扶贫办决定帮助扶贫对象推销当地特色农产品,该农产品成本价为18元每千克,销售单价y(元)与每天销售量x(千克)(x为正整数)之间满足如图所示的函数关系,其中销售单价不得低于成本价.
(1)求出y与x之间所满足的函数关系式,并写出自变量x的取值范围;
(2)当销售量为多少时,获利最大?最大利润是多少?
10.如图,抛物线与x轴交于点A和点,与y轴于直,连接,点E是对称轴上的一个动点.
(1)求抛物线的解析式;
(2)当时,求点E的坐标;
(3)在抛物线上是否存在点P,使是以为斜边的等腰直角三角形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
板块三:旋转
1.下列图形中,不是中心对称图形的是( )
A. B.
C. D.
2.在平面直角坐标系xOy中,点M与点N(3,4)关于原点对称,那么点M的坐标为( )
A.(3,4) B.(﹣3,﹣4) C.(﹣3,4) D.(3,﹣4)
3.如图,在△ABC中,AB=AC,∠BAC=50°,将△ABC绕着点A顺时针方向旋转得△ADE,AB,CE相交于点F,若AD∥CE时,则∠BAE的大小是( )
A.20° B.25° C.30° D.35°
4.如图,将△ABC绕点B逆时针旋转α,得到△EBD,若点A恰好在ED的延长线上,则∠CAD的度数为( )
A.90°﹣α B.α C.180°﹣α D.2α
5.如图,已知 中,于点E,以点B为中心,取旋转角等于,把顺时针旋转,得到,连接若,,则的大小为( )
A. B. C. D.
6.如图,以点O为旋转中心,将△ABO按顺时针方向旋转100°得到△DOF,若∠AOB=40°, 则∠DOB为 度.
7.如图,在中,,,,可以由绕点C顺时针旋转得到,其中点与点A是对应点,点与点B是对应点,连接,且A、、在同一条直线上,则的长为 .
8.如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转后得到正方形,依此方式,绕点O连续旋转2023次得到正方形,如果点A的坐标为,那么点的坐标为______.
9.如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图
(1)以A点为旋转中心,将△ABC绕点A顺时针旋转90°得△AB1C1,画出△AB1C1;
(2)作出△ABC关于坐标原点O成中心对称的△A2B2C2.
10.如图,四边形、都是正方形.
(1)如图1,若,,求的长;
(2)如图2,正方形绕点B逆时针旋转,使点G正好落在上,求证:;
(3)如图3,在(2)条件下,,,点M为直线上一动点,连接,过点作,垂足为点,直接写出的最小值为______.
同课章节目录
