第一章 勾股定理 单元测试(含简单答案) 2024-2025学年北师大版数学 八年级上册
文档属性
| 名称 | 第一章 勾股定理 单元测试(含简单答案) 2024-2025学年北师大版数学 八年级上册 | 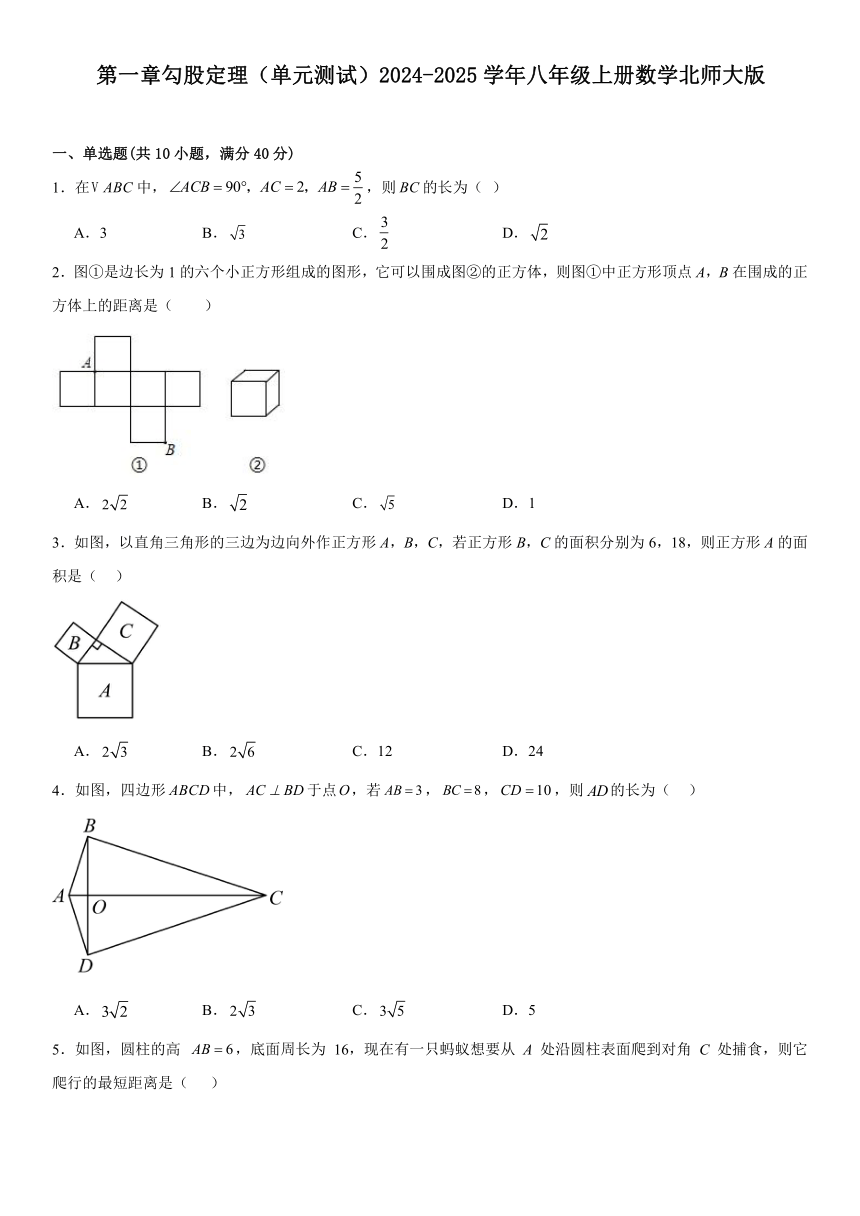 | |
| 格式 | docx | ||
| 文件大小 | 466.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 11:01:04 | ||
图片预览



文档简介
第一章勾股定理(单元测试)2024-2025学年八年级上册数学北师大版
一、单选题(共10小题,满分40分)
1.在中,,则的长为( )
A.3 B. C. D.
2.图①是边长为1的六个小正方形组成的图形,它可以围成图②的正方体,则图①中正方形顶点A,B在围成的正方体上的距离是( )
A. B. C. D.1
3.如图,以直角三角形的三边为边向外作正方形A,B,C,若正方形B,C的面积分别为6,18,则正方形A的面积是( )
A. B. C.12 D.24
4.如图,四边形中,于点,若,,,则的长为( )
A. B. C. D.5
5.如图,圆柱的高 ,底面周长为 16,现在有一只蚂蚁想要从 A 处沿圆柱表面爬到对角 C 处捕食,则它爬行的最短距离是( )
A.6 B.10 C.8 D.16
6.如图,一场暴雨过后,垂直于地面的一棵树在距地面2m处折断,树尖B恰好碰到地面,经测量AB=4m,则树高为( )
A. B. C. D.
7.如图,在中,,,分别以,为一边向外作正方形,记这两个正方形的面积分别为,,则的值为( )
A.6 B.7 C.8 D.9
8.如图Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于( )cm.
A.5 B.6 C.7 D.8
9.野外生存训练中,第一小组从营地出发向北偏东60°方向前进了3 km,第二小组向南偏东30°方向前进了3 km,第一小组准备向第二小组靠拢,则行走方向和距离分别为( ).
A.南偏西15°,km B.北偏东15°,km
C.南偏西15°,3 km D.南偏西45°,km
10.如图,甲、乙两艘轮船同时从港口 出发,甲轮船以20海里/时的速度向南偏东 方向航行,乙轮船向南偏西 方向航行. 已知它们离开港口 2时后,两艘轮船相距60海里,则乙轮船的平均速度为 ( )
A.海里/时 B.20海里/时 C.海里/时 D.海里/时
二、填空题(共8小题,满分32分)
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是9,则正方形D的边长为 .
12.在直线l上依次摆放着三个正方形(如图所示).已知斜放置的正方形的面积是1,正放置的两个正方形的面积依次是.则,1之间的关系 ;
13.如图将一根长的细木棒放入长、宽、高分别为,和的长方体无盖盒子中,则细木棒露在外面的最短长度是 .
14.如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.
15.平面直角坐标系中,已知点,且实数,满足,则点到原点的距离的最小值为 .
16.某农舍的大门是一个木制的矩形栅栏,它的高为4m,宽为3m,现需要在相对的顶点间用一块木棒加固,木板的长为 .
17.如图,将沿直线翻折得到,交于点,为的中点,连接并延长,交的延长线于点,连接,若,,的面积为,则的面积为 .
18.如图,在中,,三角形的顶点在相互平行的三条直线上,且之间的距离为1之间的距离为3,则的长是
三、解答题(共6小题,每题8分,满分48分)
19.已知在平面直角坐标系中的位置如图所示,请在网格中完成下列操作并解答问题:
(1)作关于轴对称的(其中点,分别对应点,);
(2)求出线段的长度.
20.学校需要测量旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面还多出了一段,但这条绳子的长度未知.请你应用勾股定理提出一个解决这个问题的方案(画出图形,结合图形说明需要测量的数据,把这些数据用字母表示,并用这些字母表示旗杆的高度).
21.如图,在长度为个单位长度的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的;则点、 的坐标分别为( 、 ), ( 、 )
(2)在直线上找一点在答题纸上图中标出,使的长最短,这个最短长度的平方值是
22.已知如图,在中,,D在CB的延长线上.
求证:(1);
(2)若D在CB上,结论如何,试证明你的结论.
23.(1)设a、b、c、d为正实数,a<b,c<d,bc>ad,有一个三角形的三边长分别为,,,求此三角形的面积;
(2)已知a,b均为正数,且a+b=2,求U=的最小值.
24.现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).
(1) 求线段BG的长;
(2) 现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)
参考答案:
1.C
2.B
3.D
4.C
5.B
6.C
7.D
8.C
9.A
10.D
11.3
12.
13.
14.50
15.
16.5m
17.
18.
19.(1)略
(2).
20.略
21.(1);
(2)
22.(1)11;(2)
23.(1)S△BEF= (bc﹣ad);(2)U的最小值为A′B=.
24.(1)BG=5 dm;(2)略.
一、单选题(共10小题,满分40分)
1.在中,,则的长为( )
A.3 B. C. D.
2.图①是边长为1的六个小正方形组成的图形,它可以围成图②的正方体,则图①中正方形顶点A,B在围成的正方体上的距离是( )
A. B. C. D.1
3.如图,以直角三角形的三边为边向外作正方形A,B,C,若正方形B,C的面积分别为6,18,则正方形A的面积是( )
A. B. C.12 D.24
4.如图,四边形中,于点,若,,,则的长为( )
A. B. C. D.5
5.如图,圆柱的高 ,底面周长为 16,现在有一只蚂蚁想要从 A 处沿圆柱表面爬到对角 C 处捕食,则它爬行的最短距离是( )
A.6 B.10 C.8 D.16
6.如图,一场暴雨过后,垂直于地面的一棵树在距地面2m处折断,树尖B恰好碰到地面,经测量AB=4m,则树高为( )
A. B. C. D.
7.如图,在中,,,分别以,为一边向外作正方形,记这两个正方形的面积分别为,,则的值为( )
A.6 B.7 C.8 D.9
8.如图Rt△ABC中,∠B=90°,AB=3cm,AC=5cm,将△ABC折叠,使点C与A重合,得折痕DE,则△ABE的周长等于( )cm.
A.5 B.6 C.7 D.8
9.野外生存训练中,第一小组从营地出发向北偏东60°方向前进了3 km,第二小组向南偏东30°方向前进了3 km,第一小组准备向第二小组靠拢,则行走方向和距离分别为( ).
A.南偏西15°,km B.北偏东15°,km
C.南偏西15°,3 km D.南偏西45°,km
10.如图,甲、乙两艘轮船同时从港口 出发,甲轮船以20海里/时的速度向南偏东 方向航行,乙轮船向南偏西 方向航行. 已知它们离开港口 2时后,两艘轮船相距60海里,则乙轮船的平均速度为 ( )
A.海里/时 B.20海里/时 C.海里/时 D.海里/时
二、填空题(共8小题,满分32分)
11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C的面积和是9,则正方形D的边长为 .
12.在直线l上依次摆放着三个正方形(如图所示).已知斜放置的正方形的面积是1,正放置的两个正方形的面积依次是.则,1之间的关系 ;
13.如图将一根长的细木棒放入长、宽、高分别为,和的长方体无盖盒子中,则细木棒露在外面的最短长度是 .
14.如图是由两个长方形组成的工件平面图(单位:mm),直线l是它的对称轴,能完全覆盖这个平面图形的圆面的最小半径是 mm.
15.平面直角坐标系中,已知点,且实数,满足,则点到原点的距离的最小值为 .
16.某农舍的大门是一个木制的矩形栅栏,它的高为4m,宽为3m,现需要在相对的顶点间用一块木棒加固,木板的长为 .
17.如图,将沿直线翻折得到,交于点,为的中点,连接并延长,交的延长线于点,连接,若,,的面积为,则的面积为 .
18.如图,在中,,三角形的顶点在相互平行的三条直线上,且之间的距离为1之间的距离为3,则的长是
三、解答题(共6小题,每题8分,满分48分)
19.已知在平面直角坐标系中的位置如图所示,请在网格中完成下列操作并解答问题:
(1)作关于轴对称的(其中点,分别对应点,);
(2)求出线段的长度.
20.学校需要测量旗杆的高度.同学们发现系在旗杆顶端的绳子垂到了地面还多出了一段,但这条绳子的长度未知.请你应用勾股定理提出一个解决这个问题的方案(画出图形,结合图形说明需要测量的数据,把这些数据用字母表示,并用这些字母表示旗杆的高度).
21.如图,在长度为个单位长度的正方形网格中,点、、在小正方形的顶点上.
(1)在图中画出与关于直线成轴对称的;则点、 的坐标分别为( 、 ), ( 、 )
(2)在直线上找一点在答题纸上图中标出,使的长最短,这个最短长度的平方值是
22.已知如图,在中,,D在CB的延长线上.
求证:(1);
(2)若D在CB上,结论如何,试证明你的结论.
23.(1)设a、b、c、d为正实数,a<b,c<d,bc>ad,有一个三角形的三边长分别为,,,求此三角形的面积;
(2)已知a,b均为正数,且a+b=2,求U=的最小值.
24.现有一个长、宽、高分别为5dm、4dm、3dm的无盖长方体木箱(如图,AB=5dm,BC=4dm,AE=3dm).
(1) 求线段BG的长;
(2) 现在箱外的点A处有一只蜘蛛,箱内的点C处有一只小虫正在午睡,保持不动.请你为蜘蛛设计一种捕虫方案,使得蜘蛛能以最短的路程捕捉到小虫.(木板的厚度忽略不计)
参考答案:
1.C
2.B
3.D
4.C
5.B
6.C
7.D
8.C
9.A
10.D
11.3
12.
13.
14.50
15.
16.5m
17.
18.
19.(1)略
(2).
20.略
21.(1);
(2)
22.(1)11;(2)
23.(1)S△BEF= (bc﹣ad);(2)U的最小值为A′B=.
24.(1)BG=5 dm;(2)略.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
