北京市理工附中2024~2025学年第一学期初二期中数学试卷(pdf版,无答案)
文档属性
| 名称 | 北京市理工附中2024~2025学年第一学期初二期中数学试卷(pdf版,无答案) |  | |
| 格式 | |||
| 文件大小 | 594.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 08:28:04 | ||
图片预览


文档简介
2024-2025年度初二(上)数学期中练习
班级 姓名
一、选择:(每题 2分共 2×15=30分)
1.下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm
2. 下列是几种著名的数学曲线:
(蝴蝶曲线) (笛卡尔心形线) (科赫曲线) (费马螺线)
其中不是轴对称图形的是 ( )
A.蝴蝶曲线 B.笛卡尔心形线 C.科赫曲线 D.费马螺线
3.下列计算正确的是( )
A.a+2a2=3a3 B.a3 a2=a6
C.(a3)2=a6 D.(﹣2a)2=﹣4a2
4. 如图, ABC的高表示的线段是 ( )
A.线段BC B.线段 EC
C.线段 BD D.线段CD
5. 如图,某市的三个城镇中心 A,B,C构成△ABC,该市政府打算修建一个大型体育中心 P,
使得该体育中心到三个城镇中心 A, B,C的距离相等,则 P点应设计在 ( )
A.三个角的角平分线的交点 B.三角形三条高的交点
C.三条边的垂直平分线的交点 D.三角形三条中线的交点
6. 已知等腰三角形的一个外角等于100 ,则它的顶角是( )
A.80 B. 20 C.80 或 20 D.不能确定
7. 小熊不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标
有1,2,3,4的四块),如需要拿其中的一块碎片去配一块与原来大小和形状都
一样的三角形玻璃,小熊应该拿( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
8. 如图,小陈从O点出发,前进 5米后向右转 20 ,再前进 5米后又向右转 20 , ,这样一直
走下去,他第一次回到出发点O时一共走了 ( )
A.60米 B.100米
C.90米 D.120米
9. 如图,在△ABC中,AB=AC,
∠BAD=∠CAD,给出下列结论:①△ABD≌△ACD;②∠B=∠C;
③BD=CD; ④AD⊥BC. 其中正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
10. 如图, ABC 和 DEF中,下列能判定 ABC ≌ DEF的是 ( )
A. AC DF, BC EF , A D
B. B E, C F , AC DE
C. A D , B E, C F
D. B E, C F , AC DF
11. 如图是战机在空中展示的轴对称队形.以飞机 B,C所在直线为 x轴、队形的对称轴为 y轴,
建立平面直角坐标系.若飞机 E的坐标为 (40,a),则飞机 D的坐标为
( )
A. (40, a) B. ( 40,a)
C. ( 40, a) D. (a, 40)
12. 如图,在△ABC中,根据尺规作图痕迹,下列说法
不一定正确的是( )
A. AF BF B. AFD FBC 90
C.DF AB D. BAF CAF
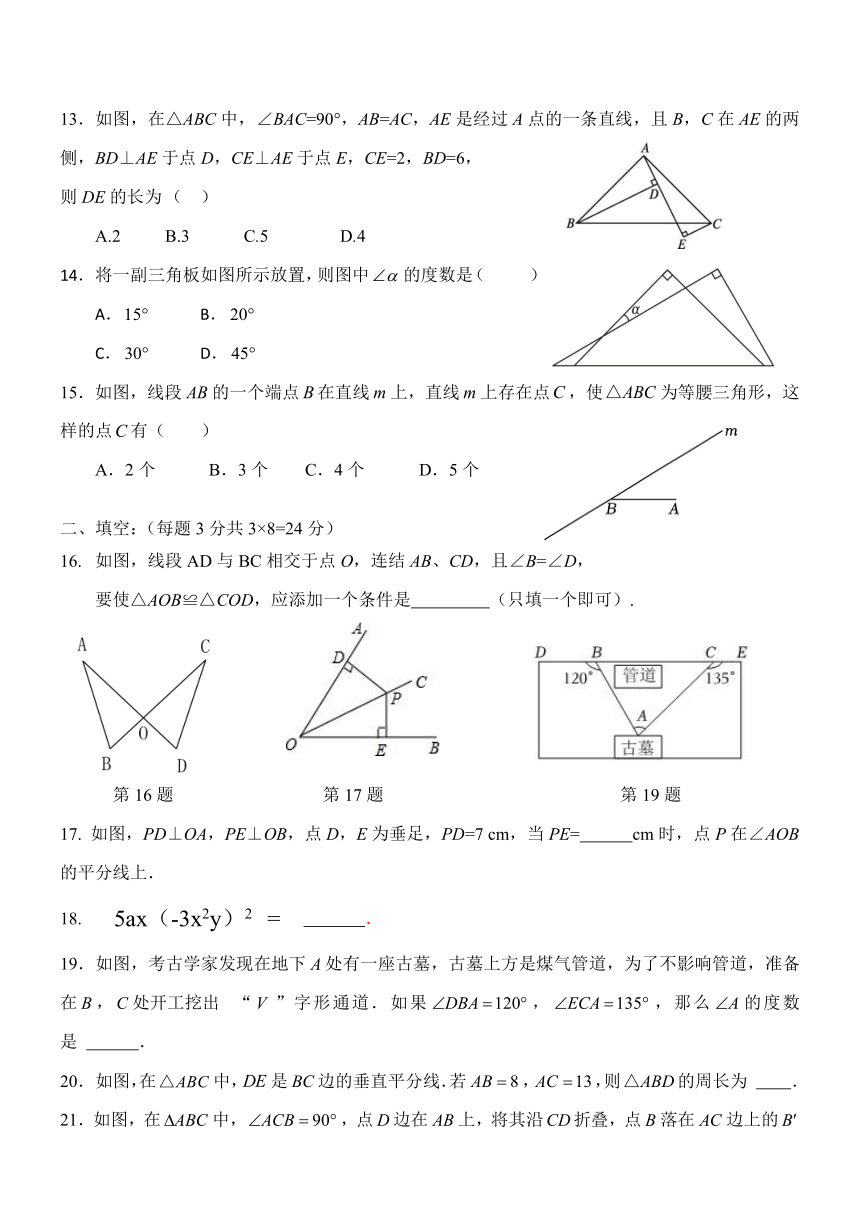
13.如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过 A点的一条直线,且 B,C在 AE的两
侧,BD⊥AE于点 D,CE⊥AE于点 E,CE=2,BD=6,
则 DE的长为( )
A.2 B.3 C.5 D.4
14.将一副三角板如图所示放置,则图中 的度数是( )
A.15 B. 20
C. 30 D. 45
15.如图,线段 AB的一个端点 B在直线m上,直线m上存在点C,使△ABC为等腰三角形,这
样的点C有( )
A.2个 B.3个 C.4个 D.5个
二、填空:(每题 3分共 3×8=24分)
16. 如图,线段 AD与 BC相交于点 O,连结 AB、CD,且∠B=∠D,
要使△AOB≌△COD,应添加一个条件是 (只填一个即可).
第 16题 第 17题 第 19题
17. 如图,PD⊥OA,PE⊥OB,点 D,E为垂足,PD=7 cm,当 PE= cm时,点 P在∠AOB
的平分线上.
18. 5ax(-3x2y)2 = .
19.如图,考古学家发现在地下 A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备
在 B,C处开工挖出 “ V ”字形通道.如果 DBA 120 , ECA 135 ,那么 A的度数
是 .
20.如图,在△ABC中,DE是 BC边的垂直平分线.若 AB 8,AC 13,则△ABD的周长为 .
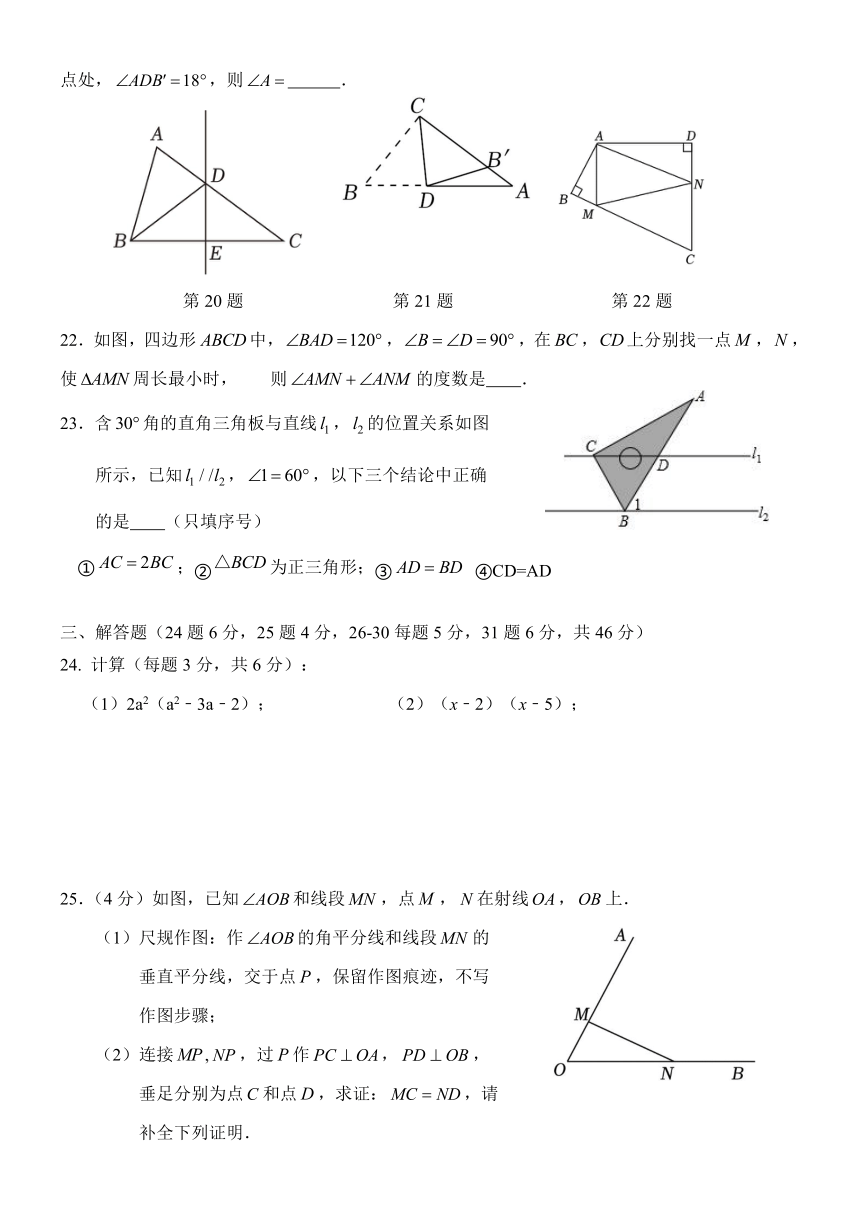
21.如图,在 ABC中, ACB 90 ,点D边在 AB上,将其沿CD折叠,点 B落在 AC边上的 B
点处, ADB 18 ,则 A .
第 20题 第 21题 第 22题
22.如图,四边形 ABCD中, BAD 120 , B D 90 ,在 BC,CD上分别找一点M ,N,
使 AMN周长最小时, 则 AMN ANM 的度数是 .
23.含 30 角的直角三角板与直线 l1, l2的位置关系如图
所示,已知 l1 / /l2, 1 60 ,以下三个结论中正确
的是 (只填序号)
① AC 2BC;②△BCD为正三角形;③ AD BD ④CD=AD
三、解答题(24题 6分,25题 4分,26-30每题 5分,31题 6分,共 46分)
24. 计算(每题 3分,共 6分):
(1)2a2(a2﹣3a﹣2); (2)(x﹣2)(x﹣5);
25.(4分)如图,已知 AOB和线段MN ,点M , N在射线OA,OB上.
(1)尺规作图:作 AOB的角平分线和线段MN 的
垂直平分线,交于点 P,保留作图痕迹,不写
作图步骤;
(2)连接MP , NP,过 P作 PC OA, PD OB,
垂足分别为点C和点D,求证:MC ND,请
补全下列证明.
证明: P在线段MN 的垂直平分线上,
MP NP, ( )
P在 AOB的角平分线上, PC OA, PD OB,
PC PD, ( )
请补全后续证明过程.
26.(5分)如图,在平面直角坐标系中, ABC的顶点
A(0,1), B(2,0),C(4,4)均在正方形网格的
格点上.
(1)画出 ABC关于 x轴对称的图形△ A1BC1,
并写出顶点C1的坐标;
(2)在 AC边上画出点D,使 ABD的面积
恰好是 ABC的面积的一半;
(3)已知 P为 x轴上一点,若 BCP与 ABC的面积相等,写出点 P的坐标.
27.(5分)已知 2m=a,32n=b,m,n 为正整数,求 23m+10n
28.(5分) 如图,已知 AB=DC,AC=DB.求证:∠1=∠2.
B C
29.(5分) 如图,点 C在线段 BD上,且 AB⊥BD,DE⊥BD,
AC⊥CE,BC=DE. 求证:AB=CD.
30.(5分) 如图,在△ABC中,∠BAC的平分线 AD交 BC于
点 D,过点 D作 DE⊥AB,DF⊥AC,垂足分别是 E,
F,连接 EF. 写出两个结论(∠BAD=∠CAD和 DE=DF
除外),并选择一个结论进行证明.
(1)_______________________________________;
(2)_______________________________________.
31.(5分)先阅读下面材料,再解决问题:
已知 x2+bx+c=0.在求关于 x的代数式的值时,可将 x2+bx+c=0 变形为 x2=﹣bx﹣c.就可以
将 x2表示为关于 x的一次多项式,从而达到“降次”的目的,我们称这样的方法为“降次代换
法”.
例如:已知 x2+2x﹣4=0,求代数式 x2(x+4)的值.
解:∵x2+2x﹣4=0,
∴x2=﹣2x+4.
∴原式=(﹣2x+4)(x+4)=﹣2x2﹣8x+4x+16=﹣2x2﹣4x+16=﹣2(﹣2x+4)﹣4x+16=4x
﹣8﹣4x+16=8.
∴x2(x+4)=8.
请用“降次代换法”,完成下列各小题:
(1)若 x2+x﹣15=0,则代数式(x+4)(x﹣3)的值为 .
(2)若 x2+5x+1=0,则代数式 x(x2+5x)+(x+7)(x﹣1)的值为 .
(3)已知 x2+2x﹣1=0,求代数式 2x4+8x3+12x2+8x+3的值.
32.(5分)在△ABC中,∠ACB=90°,延长 BC至 D,使 DC=BC,在 AB的右侧作线段 AE,
使 AE=AB,连接 DE交 AC于点 P.
(1)如图 1,在线段 PE上取点 Q,使 QE=PD,连接 AQ,求证:AP=AQ;
(2)若∠BAE=60°,依题意补全图 2,用等式表示线段 PA,PD,PE之间的数量关系,并证
明.
班级 姓名
一、选择:(每题 2分共 2×15=30分)
1.下列长度的三根小木棒能构成三角形的是( )
A.2cm,3cm,5cm B.7cm,4cm,2cm C.3cm,4cm,8cm D.3cm,3cm,4cm
2. 下列是几种著名的数学曲线:
(蝴蝶曲线) (笛卡尔心形线) (科赫曲线) (费马螺线)
其中不是轴对称图形的是 ( )
A.蝴蝶曲线 B.笛卡尔心形线 C.科赫曲线 D.费马螺线
3.下列计算正确的是( )
A.a+2a2=3a3 B.a3 a2=a6
C.(a3)2=a6 D.(﹣2a)2=﹣4a2
4. 如图, ABC的高表示的线段是 ( )
A.线段BC B.线段 EC
C.线段 BD D.线段CD
5. 如图,某市的三个城镇中心 A,B,C构成△ABC,该市政府打算修建一个大型体育中心 P,
使得该体育中心到三个城镇中心 A, B,C的距离相等,则 P点应设计在 ( )
A.三个角的角平分线的交点 B.三角形三条高的交点
C.三条边的垂直平分线的交点 D.三角形三条中线的交点
6. 已知等腰三角形的一个外角等于100 ,则它的顶角是( )
A.80 B. 20 C.80 或 20 D.不能确定
7. 小熊不慎将一块三角形的玻璃摔碎成如图所示的四块(即图中标
有1,2,3,4的四块),如需要拿其中的一块碎片去配一块与原来大小和形状都
一样的三角形玻璃,小熊应该拿( )
A. 第1块 B. 第2块 C. 第3块 D. 第4块
8. 如图,小陈从O点出发,前进 5米后向右转 20 ,再前进 5米后又向右转 20 , ,这样一直
走下去,他第一次回到出发点O时一共走了 ( )
A.60米 B.100米
C.90米 D.120米
9. 如图,在△ABC中,AB=AC,
∠BAD=∠CAD,给出下列结论:①△ABD≌△ACD;②∠B=∠C;
③BD=CD; ④AD⊥BC. 其中正确的个数是 ( )
A. 1 B. 2 C. 3 D. 4
10. 如图, ABC 和 DEF中,下列能判定 ABC ≌ DEF的是 ( )
A. AC DF, BC EF , A D
B. B E, C F , AC DE
C. A D , B E, C F
D. B E, C F , AC DF
11. 如图是战机在空中展示的轴对称队形.以飞机 B,C所在直线为 x轴、队形的对称轴为 y轴,
建立平面直角坐标系.若飞机 E的坐标为 (40,a),则飞机 D的坐标为
( )
A. (40, a) B. ( 40,a)
C. ( 40, a) D. (a, 40)
12. 如图,在△ABC中,根据尺规作图痕迹,下列说法
不一定正确的是( )
A. AF BF B. AFD FBC 90
C.DF AB D. BAF CAF
13.如图,在△ABC中,∠BAC=90°,AB=AC,AE是经过 A点的一条直线,且 B,C在 AE的两
侧,BD⊥AE于点 D,CE⊥AE于点 E,CE=2,BD=6,
则 DE的长为( )
A.2 B.3 C.5 D.4
14.将一副三角板如图所示放置,则图中 的度数是( )
A.15 B. 20
C. 30 D. 45
15.如图,线段 AB的一个端点 B在直线m上,直线m上存在点C,使△ABC为等腰三角形,这
样的点C有( )
A.2个 B.3个 C.4个 D.5个
二、填空:(每题 3分共 3×8=24分)
16. 如图,线段 AD与 BC相交于点 O,连结 AB、CD,且∠B=∠D,
要使△AOB≌△COD,应添加一个条件是 (只填一个即可).
第 16题 第 17题 第 19题
17. 如图,PD⊥OA,PE⊥OB,点 D,E为垂足,PD=7 cm,当 PE= cm时,点 P在∠AOB
的平分线上.
18. 5ax(-3x2y)2 = .
19.如图,考古学家发现在地下 A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备
在 B,C处开工挖出 “ V ”字形通道.如果 DBA 120 , ECA 135 ,那么 A的度数
是 .
20.如图,在△ABC中,DE是 BC边的垂直平分线.若 AB 8,AC 13,则△ABD的周长为 .
21.如图,在 ABC中, ACB 90 ,点D边在 AB上,将其沿CD折叠,点 B落在 AC边上的 B
点处, ADB 18 ,则 A .
第 20题 第 21题 第 22题
22.如图,四边形 ABCD中, BAD 120 , B D 90 ,在 BC,CD上分别找一点M ,N,
使 AMN周长最小时, 则 AMN ANM 的度数是 .
23.含 30 角的直角三角板与直线 l1, l2的位置关系如图
所示,已知 l1 / /l2, 1 60 ,以下三个结论中正确
的是 (只填序号)
① AC 2BC;②△BCD为正三角形;③ AD BD ④CD=AD
三、解答题(24题 6分,25题 4分,26-30每题 5分,31题 6分,共 46分)
24. 计算(每题 3分,共 6分):
(1)2a2(a2﹣3a﹣2); (2)(x﹣2)(x﹣5);
25.(4分)如图,已知 AOB和线段MN ,点M , N在射线OA,OB上.
(1)尺规作图:作 AOB的角平分线和线段MN 的
垂直平分线,交于点 P,保留作图痕迹,不写
作图步骤;
(2)连接MP , NP,过 P作 PC OA, PD OB,
垂足分别为点C和点D,求证:MC ND,请
补全下列证明.
证明: P在线段MN 的垂直平分线上,
MP NP, ( )
P在 AOB的角平分线上, PC OA, PD OB,
PC PD, ( )
请补全后续证明过程.
26.(5分)如图,在平面直角坐标系中, ABC的顶点
A(0,1), B(2,0),C(4,4)均在正方形网格的
格点上.
(1)画出 ABC关于 x轴对称的图形△ A1BC1,
并写出顶点C1的坐标;
(2)在 AC边上画出点D,使 ABD的面积
恰好是 ABC的面积的一半;
(3)已知 P为 x轴上一点,若 BCP与 ABC的面积相等,写出点 P的坐标.
27.(5分)已知 2m=a,32n=b,m,n 为正整数,求 23m+10n
28.(5分) 如图,已知 AB=DC,AC=DB.求证:∠1=∠2.
B C
29.(5分) 如图,点 C在线段 BD上,且 AB⊥BD,DE⊥BD,
AC⊥CE,BC=DE. 求证:AB=CD.
30.(5分) 如图,在△ABC中,∠BAC的平分线 AD交 BC于
点 D,过点 D作 DE⊥AB,DF⊥AC,垂足分别是 E,
F,连接 EF. 写出两个结论(∠BAD=∠CAD和 DE=DF
除外),并选择一个结论进行证明.
(1)_______________________________________;
(2)_______________________________________.
31.(5分)先阅读下面材料,再解决问题:
已知 x2+bx+c=0.在求关于 x的代数式的值时,可将 x2+bx+c=0 变形为 x2=﹣bx﹣c.就可以
将 x2表示为关于 x的一次多项式,从而达到“降次”的目的,我们称这样的方法为“降次代换
法”.
例如:已知 x2+2x﹣4=0,求代数式 x2(x+4)的值.
解:∵x2+2x﹣4=0,
∴x2=﹣2x+4.
∴原式=(﹣2x+4)(x+4)=﹣2x2﹣8x+4x+16=﹣2x2﹣4x+16=﹣2(﹣2x+4)﹣4x+16=4x
﹣8﹣4x+16=8.
∴x2(x+4)=8.
请用“降次代换法”,完成下列各小题:
(1)若 x2+x﹣15=0,则代数式(x+4)(x﹣3)的值为 .
(2)若 x2+5x+1=0,则代数式 x(x2+5x)+(x+7)(x﹣1)的值为 .
(3)已知 x2+2x﹣1=0,求代数式 2x4+8x3+12x2+8x+3的值.
32.(5分)在△ABC中,∠ACB=90°,延长 BC至 D,使 DC=BC,在 AB的右侧作线段 AE,
使 AE=AB,连接 DE交 AC于点 P.
(1)如图 1,在线段 PE上取点 Q,使 QE=PD,连接 AQ,求证:AP=AQ;
(2)若∠BAE=60°,依题意补全图 2,用等式表示线段 PA,PD,PE之间的数量关系,并证
明.
同课章节目录
