浙江省宁波市十二校联考2024-2025学年上学期七年级数学期中测试卷(含答案)
文档属性
| 名称 | 浙江省宁波市十二校联考2024-2025学年上学期七年级数学期中测试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 44.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 21:31:44 | ||
图片预览


文档简介
2024 学年第一学期七年级数学学科期中测试卷
一. 选择题 (每小题 3 分, 共 30 分)
1.2024 的相反数是 ( )
A. 2024 B. -2024 C. D.
2. 已知下列各数: ,其中负有理数有 ( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
3. 宁波市商务局发布的统计数据显示, 2024 年 10 月 1 日至 7 日, 全市重点监测的 50 家零售、餐饮企业累计实现销售额 915000000 元, 较去年同期略有增长。将数据 915000000 用科学记数法表示应为 ( )
A. B. C. D.
4. 下列说法中正确的个数是 ( )
① 0 是绝对值最小的有理数 ②相反数大于本身的数是负数 ③一个有理数不是整数就是分数 ④一个有理数不是正数就是负数 ⑤无理数都可以用数轴上的点来表示 ⑥一个数的立方根有两个, 它们互为相反数
A. 2 B. 3 C. 4 D. 5
5. 用2,0,2,4这四个数进行如下运算,计算结果最大的式子是 ( )
A. B. C. D.
6. 面积为 15 的正方形的边长为 ,则 的值在 ( )
A. 1 和 2 之间 B. 2 和 3 之间 C. 3 和 4 之间 D. 4 和 5 之间
7. 用 表示的数一定是 ( )
A. 正数 B. 负数 C. 正数或负数 D. 都不对
8. 一台电视机成本价为 元,销售价比成本价增加了 ,因库存积压,所以就按销售价的 出售,那么每台实际售价为 ( )
A. 元 B. 元
C. 元 D. 元
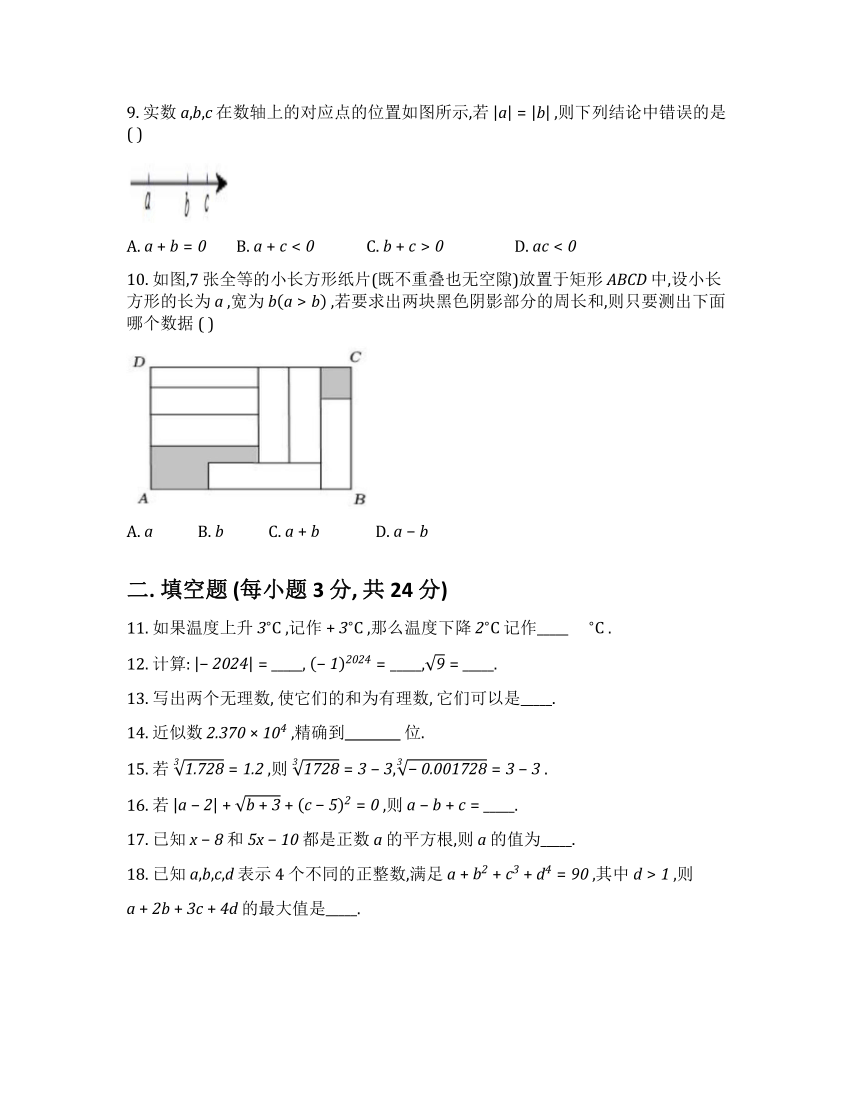
9. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( )
A. B. C. D.
10. 如图,7 张全等的小长方形纸片(既不重叠也无空隙)放置于矩形 中,设小长方形的长为 ,宽为 ,若要求出两块黑色阴影部分的周长和,则只要测出下面哪个数据 ( )
A. B. C. D.
二. 填空题 (每小题 3 分, 共 24 分)
11. 如果温度上升 ,记作 ,那么温度下降 记作_____ .
12. 计算: _____, _____.
13. 写出两个无理数, 使它们的和为有理数, 它们可以是_____.
14. 近似数 ,精确到 位.
15. 若 ,则 .
16. 若 ,则 _____.
17. 已知 和 都是正数 的平方根,则 的值为_____.
18. 已知 表示 4 个不同的正整数,满足 ,其中 ,则
的最大值是_____.
三、解答题 (19 题 10 分, 20 题 7 分, 21 题 8 分, 22 题 11 分, 23 题 10 分, 共 46 分)
19. 计算:
(1). (2).
. (4).
20. 某水果店以每箱 90 元的价格从水果批发市场购进 20 箱樱桃, 若以每箱净重 5 千克为标准, 超过的千克数记为正数, 不足的千克数记为负数, 称重的记录如表:
与标准重量的差值(单 位: 千克) - 0.5 - 0.25 0 0.2 0.25 0.5
箱数 2 2 4 5 n 3
(1) 求 的值及这 20 箱樱桃的总重量;
(2)该水果店第一天以每千克 25 元的价格销售了这批樱桃的 70%, 第二天因为害怕剩余樱桃腐烂, 决定降价把剩余的樱桃以第一天零售价的 60%全部售出. 水果店在销售这批樱桃过程中是盈利还是亏损, 盈利或亏损多少元
21. 初中阶段, 目前我们已经学习了多种计算技巧, 例如裂项相消法、错位相减法等, 请计算下列各式:
(1) _____;
(2) _____;
(3) _____;
(4) _____.
22. 结合数轴与绝对值的知识, 回答下列问题:
(1)数轴上表示 4 和 1 的两点之间的距离是_____;表示 -3 和 2 的两点之间的距离是_____; 一般地,数轴上表示数 和 的两点之间的距离等于 ,数轴上表示 和 -1 的两点之间的距离是_____;如果表示数 和 -2 的两点之间的距离是 3, 那么 _____.
(2)若数轴上表示 的点位于 -5 和 3 之间,求 的值.
(3)当 为_____时, 最小,最小值为_____.
(4)若 ,请直接写出 的值.
23. 如图,数轴上有 两点, 之间距离为 21,原点 在 之间, 到 的距离是 到 的距离的两倍.
(1)点 表示的数为_____,点 表示的数为_____;
(2)点 、点 和点 (点 初始位置在原点 ) 同时向左运动,它们的速度分别为 1 , 2,2 个单位长度每秒,则经过多少秒,点 到点 与点 的距离相等
(3)点 沿着数轴移动,每次只允许移动 1 个单位长度,经过 8 次移动后,点 与原点 相距 1 个单位长度. 满足条件的点 的移动方法共有多少种
(4)点 和点 同时沿着数轴移动,两点每次均只允许移动 1 个单位长度. 请判断点 和点 经过相同次数的移动后,能否同时到达原点 如果能,请给出点 和点 各自的移动方法; 如果不能, 请说明理由.
2024 学年第一学期七年级数学学科期中测试卷答案
一. 选择题 (每小题 3 分, 共 30 分)
1 2 3 4 5 6 7 8 9 10
B C A C B C D A B A
二. 填空题 (每小题 3 分, 共 24 分)
11. -2 12. 2024 1 3 13. 和 (答案不唯一)
14. 十 17. 或 25 18. 81
三、解答题 (19 题 10 分, 20 题 7 分, 21 题 8 分, 22 题 11 分, 23 题 10 分, 共 46 分)
19. (1) -40 (2) -6 (3) 2 (4) -10.25
(第 (1) (2) 题每题 2 分, 第 (3) (4) 题每题 3 分)
(1) (1 分)
(千克) (2 分)
(2) (元) (4 分)
21. (1) (2) (3) (4)
(每小题 2 分)
22. (1) 或 1 (前 3 空每空 1 分,最后一空 2 分)
(2)
(2 分)
(3) -1 7 (2 分) (4) 或 -3 (2 分)
23. (1) -14 7 (2 分)
(2) 或
(3) 9 种 (2 分)
(4)不能同时到达原点 (1 分)
理由: ,两数之和为奇数,而 ,为偶数
若两点同时向左平移一个单位, 它们的和-2; 若两点同时向右平移一个单位, 它们的和+2;
若两点一左一右平移, 则它们的和不变;
综上所述, 平移后这两点所表示的数之和必为奇数, 因此不能同时达到原点 (1 分) 学小屋
一. 选择题 (每小题 3 分, 共 30 分)
1.2024 的相反数是 ( )
A. 2024 B. -2024 C. D.
2. 已知下列各数: ,其中负有理数有 ( )
A. 1 个 B. 2 个 C. 3 个 D. 4 个
3. 宁波市商务局发布的统计数据显示, 2024 年 10 月 1 日至 7 日, 全市重点监测的 50 家零售、餐饮企业累计实现销售额 915000000 元, 较去年同期略有增长。将数据 915000000 用科学记数法表示应为 ( )
A. B. C. D.
4. 下列说法中正确的个数是 ( )
① 0 是绝对值最小的有理数 ②相反数大于本身的数是负数 ③一个有理数不是整数就是分数 ④一个有理数不是正数就是负数 ⑤无理数都可以用数轴上的点来表示 ⑥一个数的立方根有两个, 它们互为相反数
A. 2 B. 3 C. 4 D. 5
5. 用2,0,2,4这四个数进行如下运算,计算结果最大的式子是 ( )
A. B. C. D.
6. 面积为 15 的正方形的边长为 ,则 的值在 ( )
A. 1 和 2 之间 B. 2 和 3 之间 C. 3 和 4 之间 D. 4 和 5 之间
7. 用 表示的数一定是 ( )
A. 正数 B. 负数 C. 正数或负数 D. 都不对
8. 一台电视机成本价为 元,销售价比成本价增加了 ,因库存积压,所以就按销售价的 出售,那么每台实际售价为 ( )
A. 元 B. 元
C. 元 D. 元
9. 实数 在数轴上的对应点的位置如图所示,若 ,则下列结论中错误的是( )
A. B. C. D.
10. 如图,7 张全等的小长方形纸片(既不重叠也无空隙)放置于矩形 中,设小长方形的长为 ,宽为 ,若要求出两块黑色阴影部分的周长和,则只要测出下面哪个数据 ( )
A. B. C. D.
二. 填空题 (每小题 3 分, 共 24 分)
11. 如果温度上升 ,记作 ,那么温度下降 记作_____ .
12. 计算: _____, _____.
13. 写出两个无理数, 使它们的和为有理数, 它们可以是_____.
14. 近似数 ,精确到 位.
15. 若 ,则 .
16. 若 ,则 _____.
17. 已知 和 都是正数 的平方根,则 的值为_____.
18. 已知 表示 4 个不同的正整数,满足 ,其中 ,则
的最大值是_____.
三、解答题 (19 题 10 分, 20 题 7 分, 21 题 8 分, 22 题 11 分, 23 题 10 分, 共 46 分)
19. 计算:
(1). (2).
. (4).
20. 某水果店以每箱 90 元的价格从水果批发市场购进 20 箱樱桃, 若以每箱净重 5 千克为标准, 超过的千克数记为正数, 不足的千克数记为负数, 称重的记录如表:
与标准重量的差值(单 位: 千克) - 0.5 - 0.25 0 0.2 0.25 0.5
箱数 2 2 4 5 n 3
(1) 求 的值及这 20 箱樱桃的总重量;
(2)该水果店第一天以每千克 25 元的价格销售了这批樱桃的 70%, 第二天因为害怕剩余樱桃腐烂, 决定降价把剩余的樱桃以第一天零售价的 60%全部售出. 水果店在销售这批樱桃过程中是盈利还是亏损, 盈利或亏损多少元
21. 初中阶段, 目前我们已经学习了多种计算技巧, 例如裂项相消法、错位相减法等, 请计算下列各式:
(1) _____;
(2) _____;
(3) _____;
(4) _____.
22. 结合数轴与绝对值的知识, 回答下列问题:
(1)数轴上表示 4 和 1 的两点之间的距离是_____;表示 -3 和 2 的两点之间的距离是_____; 一般地,数轴上表示数 和 的两点之间的距离等于 ,数轴上表示 和 -1 的两点之间的距离是_____;如果表示数 和 -2 的两点之间的距离是 3, 那么 _____.
(2)若数轴上表示 的点位于 -5 和 3 之间,求 的值.
(3)当 为_____时, 最小,最小值为_____.
(4)若 ,请直接写出 的值.
23. 如图,数轴上有 两点, 之间距离为 21,原点 在 之间, 到 的距离是 到 的距离的两倍.
(1)点 表示的数为_____,点 表示的数为_____;
(2)点 、点 和点 (点 初始位置在原点 ) 同时向左运动,它们的速度分别为 1 , 2,2 个单位长度每秒,则经过多少秒,点 到点 与点 的距离相等
(3)点 沿着数轴移动,每次只允许移动 1 个单位长度,经过 8 次移动后,点 与原点 相距 1 个单位长度. 满足条件的点 的移动方法共有多少种
(4)点 和点 同时沿着数轴移动,两点每次均只允许移动 1 个单位长度. 请判断点 和点 经过相同次数的移动后,能否同时到达原点 如果能,请给出点 和点 各自的移动方法; 如果不能, 请说明理由.
2024 学年第一学期七年级数学学科期中测试卷答案
一. 选择题 (每小题 3 分, 共 30 分)
1 2 3 4 5 6 7 8 9 10
B C A C B C D A B A
二. 填空题 (每小题 3 分, 共 24 分)
11. -2 12. 2024 1 3 13. 和 (答案不唯一)
14. 十 17. 或 25 18. 81
三、解答题 (19 题 10 分, 20 题 7 分, 21 题 8 分, 22 题 11 分, 23 题 10 分, 共 46 分)
19. (1) -40 (2) -6 (3) 2 (4) -10.25
(第 (1) (2) 题每题 2 分, 第 (3) (4) 题每题 3 分)
(1) (1 分)
(千克) (2 分)
(2) (元) (4 分)
21. (1) (2) (3) (4)
(每小题 2 分)
22. (1) 或 1 (前 3 空每空 1 分,最后一空 2 分)
(2)
(2 分)
(3) -1 7 (2 分) (4) 或 -3 (2 分)
23. (1) -14 7 (2 分)
(2) 或
(3) 9 种 (2 分)
(4)不能同时到达原点 (1 分)
理由: ,两数之和为奇数,而 ,为偶数
若两点同时向左平移一个单位, 它们的和-2; 若两点同时向右平移一个单位, 它们的和+2;
若两点一左一右平移, 则它们的和不变;
综上所述, 平移后这两点所表示的数之和必为奇数, 因此不能同时达到原点 (1 分) 学小屋
同课章节目录
