选择必修第二册 第四章 4.1 数列的概念(第2课时) 课件(共21张PPT)
文档属性
| 名称 | 选择必修第二册 第四章 4.1 数列的概念(第2课时) 课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
选择必修
第四章 数列
4.1 数列的概念(第2课时)
教学目标
学习目标 数学素养
1.理解数列递推公式的含义,会用递推公式解决有关问题. 1.逻辑推理素养和数学运算素养.
2.理解数列的前 n 项和公式的定义,会利用前 n 项和公式与通项公式的关系求通项公式. 2.数学抽象素养和数学运算素养.
温故知新
1.数列的概念
把按照确定的顺序排列的一列数称为数列.
数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
2.数列的分类
类别 含义
按项数
按项的变化趋势
有穷数列
无穷数列
项数有限的数列叫做有穷数列
项数无限的数列叫做有穷数列
递增数列
从第2项起,每一项都大于它的前一项的数列叫做递增数列
递减数列
从第2项起,每一项都小于它的前一项的数列叫做递减数列
常数列
各项都相等的数列叫做常数列
摆动数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫做摆动数列
温故知新
3.数列的表示
①按顺序一一列举:a1,a2,a3,…,an,… 简记{an}
②列表法
③图象法
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
④通项公式法
新知探究
【例1】如果数列{}的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
令n2+2n=120 ,
n=-12(舍)或n=10,
解:
分析:要判定120是不是数列{}中的项,就是要回答是否存在正整数n,使得n2+2n=120.也就是判断这个关于n的方程是否有正整数解.
所以,120是数列{}中的项,是第10项.
解这个关于n的方程,得
思考:已知数列通项,我们可以解决哪些问题呢?
①可以知道数列中的某一项的值;
②可以判断这个数值是不是该数列的项.
初试身手
⑴∵f(x)=,
1. 已知函数f(x)=(x≥1),构造数列an=f(n)(n∈N*).
⑴求证:an>-2;
⑵数列{an}是递增数列还是递减数列?为什么?
∴.
又n∈N*,
解:
∴an>-2.
⑵数列{an}是递减数列.
∵,
∴<0,
即an+1∴数列{an}是递减数列.
知新探究
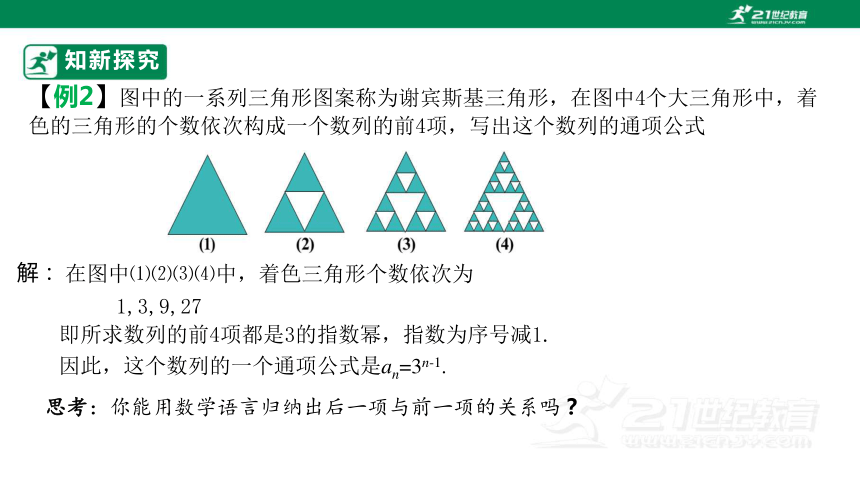
在图中⑴⑵⑶⑷中,着色三角形个数依次为
1,3,9,27
即所求数列的前4项都是3的指数幂,指数为序号减1.
【例2】图中的一系列三角形图案称为谢宾斯基三角形,在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的通项公式
解:
因此,这个数列的一个通项公式是an=3n-1.
思考:你能用数学语言归纳出后一项与前一项的关系吗?
知新探究
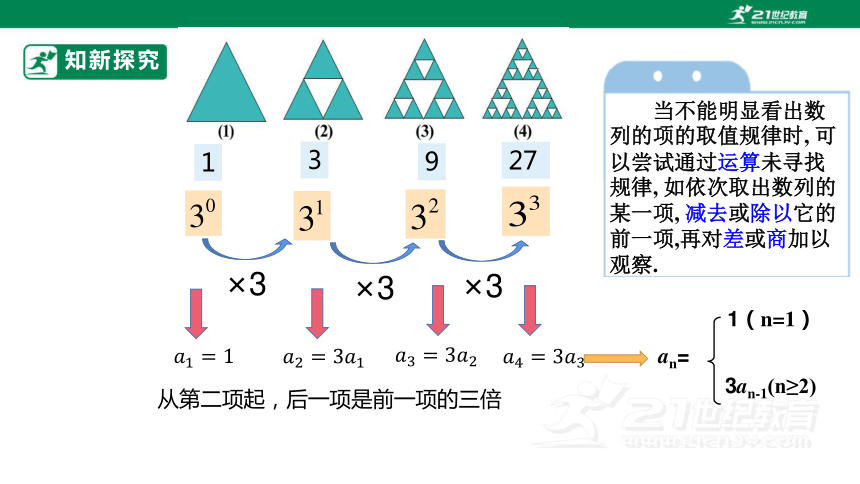
当不能明显看出数列的项的取值规律时, 可以尝试通过运算未寻找规律, 如依次取出数列的某一项, 减去或除以它的前一项,再对差或商加以观察.
1
3
9
27
×3
×3
×3
.......
3an-1(n≥2)
1(n=1)
an=
从第二项起,后一项是前一项的三倍
知新探究
象这样,
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
观察下面的数列,你能发现什么结论?并用数学语言表示出来.
1,1,2,3,5,8,13,21,34,…
从第3项起,每一项都等于它的前面两项的和.
即.
裴波那契数列
知新探究
象这样,
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
递推公式也是数列的一种表示方法.
思考:递推公式和通项公式有什么区别和联系?
通项公式 递推公式
联系 区别 定义
求解
都能确定一个数列
项与序号的关系
项与项的关系
不需要其它条件
需要初始条件
知新探究
【例3】已知数列{an}的首项为a1=1,递推公式为,写出这个数列的前5项.
解:
由题意可知
a1=1,
,
,
,
.
知新探究
在数列研究中,求数列某些项的和是主要研究问题之一.
例3中,可以求出这个数列的前5项和.
数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,即Sn=a1+a2+…+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
探索数列的求和公式,曾是古代算学家非常感兴趣的问题.
显然S1=a1,而Sn-1=a1+a2+…+an-1(n≥2) ,于是我们有
.
当n≥2时,有
Sn=a1+a2+…+an. ①
Sn-1=a1+a2+…+an-1. ②
由①-②得
an=Sn-Sn-1.
知新探究
∵a1=S1=2,
当n≥2时,an=Sn-Sn-1
= n2+n-[(n-1) +(n-1)]
=2n.
并且当n=1时,a1=2×1=2依然成立.
∴{an} 的通项公式是an=2n.
已知数列{an} 的前n项和公式为 Sn =n2 +n,你能求出{an} 的通项公式吗?
初试身手
2.已知数列{an}的前几项和公式为Sn =-n2+5 ,求{an}的通项公式.
解:
当n=1时,a1=S1=-1+5=4;
将n=1代入①式得,-2+1=-1≠4=a1,
当n≥2时, an=Sn-Sn-1=-(n2+5)-[-(n-1)2+5]=-2n+1. ①
∴当n=1时,①式不成立.
∴.
知新探究
【例4】已知数列{an}满足a1=-1,an+1=an+,n∈N*,求数列{an}的通项公式an.
解:
∵,
∴.
以上各式累加,得
.
∵a1=-1,,
∴.
当n=1时,a1=-1,符合上式.
∴数列{an}的通项公式为.
初试身手
∵a1=1,an=(n≥2),
∴,
3.设数列{an}中,a1=1,an=(n≥2),求数列{an}的通项公式an.
.
.
解:
当n=1时,a1=1,符合上式.
∴数列{an}的通项公式是.
课堂小结
1.数列的递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
2.数列的前n项和
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
递推公式也是数列的一种表示方法.
数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,即Sn=a1+a2+…+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
.
作业布置
作业: P8 练习 第3,4题
P8-9 习题4.1 第2⑶⑷,4,5,6,7题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
选择必修
第四章 数列
4.1 数列的概念(第2课时)
教学目标
学习目标 数学素养
1.理解数列递推公式的含义,会用递推公式解决有关问题. 1.逻辑推理素养和数学运算素养.
2.理解数列的前 n 项和公式的定义,会利用前 n 项和公式与通项公式的关系求通项公式. 2.数学抽象素养和数学运算素养.
温故知新
1.数列的概念
把按照确定的顺序排列的一列数称为数列.
数列{an}是从正整数集N﹡(或它的有限子集{1,2,…,n})到实数集R的函数,其自变量是序号n,对应的函数值是数列的第n项an,记为an=f(n).
2.数列的分类
类别 含义
按项数
按项的变化趋势
有穷数列
无穷数列
项数有限的数列叫做有穷数列
项数无限的数列叫做有穷数列
递增数列
从第2项起,每一项都大于它的前一项的数列叫做递增数列
递减数列
从第2项起,每一项都小于它的前一项的数列叫做递减数列
常数列
各项都相等的数列叫做常数列
摆动数列
从第2项起,有些项大于它的前一项,有些项小于它的前一项的数列,叫做摆动数列
温故知新
3.数列的表示
①按顺序一一列举:a1,a2,a3,…,an,… 简记{an}
②列表法
③图象法
如果数列{an}的第n项an与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的通项公式.
通项公式就是数列的函数解析式,根据通项公式可以写出数列的各项.
④通项公式法
新知探究
【例1】如果数列{}的通项公式为,那么120是不是这个数列的项?如果是,是第几项?
令n2+2n=120 ,
n=-12(舍)或n=10,
解:
分析:要判定120是不是数列{}中的项,就是要回答是否存在正整数n,使得n2+2n=120.也就是判断这个关于n的方程是否有正整数解.
所以,120是数列{}中的项,是第10项.
解这个关于n的方程,得
思考:已知数列通项,我们可以解决哪些问题呢?
①可以知道数列中的某一项的值;
②可以判断这个数值是不是该数列的项.
初试身手
⑴∵f(x)=,
1. 已知函数f(x)=(x≥1),构造数列an=f(n)(n∈N*).
⑴求证:an>-2;
⑵数列{an}是递增数列还是递减数列?为什么?
∴.
又n∈N*,
解:
∴an>-2.
⑵数列{an}是递减数列.
∵,
∴<0,
即an+1
知新探究
在图中⑴⑵⑶⑷中,着色三角形个数依次为
1,3,9,27
即所求数列的前4项都是3的指数幂,指数为序号减1.
【例2】图中的一系列三角形图案称为谢宾斯基三角形,在图中4个大三角形中,着色的三角形的个数依次构成一个数列的前4项,写出这个数列的通项公式
解:
因此,这个数列的一个通项公式是an=3n-1.
思考:你能用数学语言归纳出后一项与前一项的关系吗?
知新探究
当不能明显看出数列的项的取值规律时, 可以尝试通过运算未寻找规律, 如依次取出数列的某一项, 减去或除以它的前一项,再对差或商加以观察.
1
3
9
27
×3
×3
×3
.......
3an-1(n≥2)
1(n=1)
an=
从第二项起,后一项是前一项的三倍
知新探究
象这样,
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
观察下面的数列,你能发现什么结论?并用数学语言表示出来.
1,1,2,3,5,8,13,21,34,…
从第3项起,每一项都等于它的前面两项的和.
即.
裴波那契数列
知新探究
象这样,
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
递推公式也是数列的一种表示方法.
思考:递推公式和通项公式有什么区别和联系?
通项公式 递推公式
联系 区别 定义
求解
都能确定一个数列
项与序号的关系
项与项的关系
不需要其它条件
需要初始条件
知新探究
【例3】已知数列{an}的首项为a1=1,递推公式为,写出这个数列的前5项.
解:
由题意可知
a1=1,
,
,
,
.
知新探究
在数列研究中,求数列某些项的和是主要研究问题之一.
例3中,可以求出这个数列的前5项和.
数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,即Sn=a1+a2+…+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
探索数列的求和公式,曾是古代算学家非常感兴趣的问题.
显然S1=a1,而Sn-1=a1+a2+…+an-1(n≥2) ,于是我们有
.
当n≥2时,有
Sn=a1+a2+…+an. ①
Sn-1=a1+a2+…+an-1. ②
由①-②得
an=Sn-Sn-1.
知新探究
∵a1=S1=2,
当n≥2时,an=Sn-Sn-1
= n2+n-[(n-1) +(n-1)]
=2n.
并且当n=1时,a1=2×1=2依然成立.
∴{an} 的通项公式是an=2n.
已知数列{an} 的前n项和公式为 Sn =n2 +n,你能求出{an} 的通项公式吗?
初试身手
2.已知数列{an}的前几项和公式为Sn =-n2+5 ,求{an}的通项公式.
解:
当n=1时,a1=S1=-1+5=4;
将n=1代入①式得,-2+1=-1≠4=a1,
当n≥2时, an=Sn-Sn-1=-(n2+5)-[-(n-1)2+5]=-2n+1. ①
∴当n=1时,①式不成立.
∴.
知新探究
【例4】已知数列{an}满足a1=-1,an+1=an+,n∈N*,求数列{an}的通项公式an.
解:
∵,
∴.
以上各式累加,得
.
∵a1=-1,,
∴.
当n=1时,a1=-1,符合上式.
∴数列{an}的通项公式为.
初试身手
∵a1=1,an=(n≥2),
∴,
3.设数列{an}中,a1=1,an=(n≥2),求数列{an}的通项公式an.
.
.
解:
当n=1时,a1=1,符合上式.
∴数列{an}的通项公式是.
课堂小结
1.数列的递推公式
如果一个数列的相邻两项或多项之间的关系可以用一个式子来表示,那么这个式子叫做这个数列的递推公式.
2.数列的前n项和
知道了首项或前几项以及递推公式,就能求出数列的每一项了.
递推公式也是数列的一种表示方法.
数列{an}从第1项起到第n项止的各项之和,称为数列{an}的前n项和,记作Sn,即Sn=a1+a2+…+an.
如果数列{an}的前n项和Sn与它的序号n之间的对应关系可以用一个式子来表示,那么这个式子叫做这个数列的前n项和公式.
.
作业布置
作业: P8 练习 第3,4题
P8-9 习题4.1 第2⑶⑷,4,5,6,7题.
尽情享受学习数学的快乐吧!
我们下节课再见!
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
