7.4数学建模活动:周期现象的描述 同步练习(含解析)-高中数学人教B版(2019)必修第三册
文档属性
| 名称 | 7.4数学建模活动:周期现象的描述 同步练习(含解析)-高中数学人教B版(2019)必修第三册 |

|
|
| 格式 | docx | ||
| 文件大小 | 495.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-06 16:34:48 | ||
图片预览




文档简介
7.4 数学建模活动:周期现象的描述(同步练习)- 高中数学人教B版(2019)必修第三册
一、选择题
1.某巨型摩天轮.其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第35分钟时他距地面大约为米.
A.75 B.85 C.100 D.110
2.下表是某市近30年来月平均气温(℃)的数据统计表:
月份 1 2 3 4 5 6 7 8 9 10 11 12
月平均气温 -5.9 -3.3 2.2 9.3 15.1 20.3 22.8 22.2 18.2 11.9 4.3 -2.4
则适合这组数据的函数模型是( )
A.
B.(,)
C.(,)
D.
3.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则t为(秒)时的电流强度为( )
A.0 B. C. D.
4.某人的血压满足函数解析式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
5.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
6.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
7.甲地某天6h至14h的温度变化曲线如图所示,其近似满足函数,则该天8h的温度大约为( )
A.16 B.15 C.14 D.13
8.已知某帆船中心比赛场馆区的海面上海浪高度:y(米)可看作时间t(,单位:时)的函数,记作,经长期观测, 的曲线可近似地看成是函数的图象,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
2 1.5 1 1.5 2 1.5 0.99 1.5 2
则最能近似地表示表中数据间对应关系的函数是( )
A. B.
C. D.
二、填空题
9.如图,某地一天从6~14时的温度变化曲线近似满足函数,,则这段曲线的函数解析式为_________.
10.潮汐是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动.习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流.早先的人们为了表示生潮的时刻,把发生在早晨的高潮叫潮,发生在晚上的高潮叫汐,这是潮汐名称的由来.下表中给出了某市码头某一天水深与时间的关系(夜间零点开始计时).
时刻(t) 0 2 4 6 8 10 12
水深(y)单位:米 5.0 4.8 4.7 4.6 4.4 4.3 4.2
时刻(t) 14 16 18 20 22 24
水深(y)单位:米 4.3 4.4 4.6 4.7 4.8 5.0
用函数模型(,)来近似地描述这些数据,则________.
11.已知函数的定义域为R,且,,则______
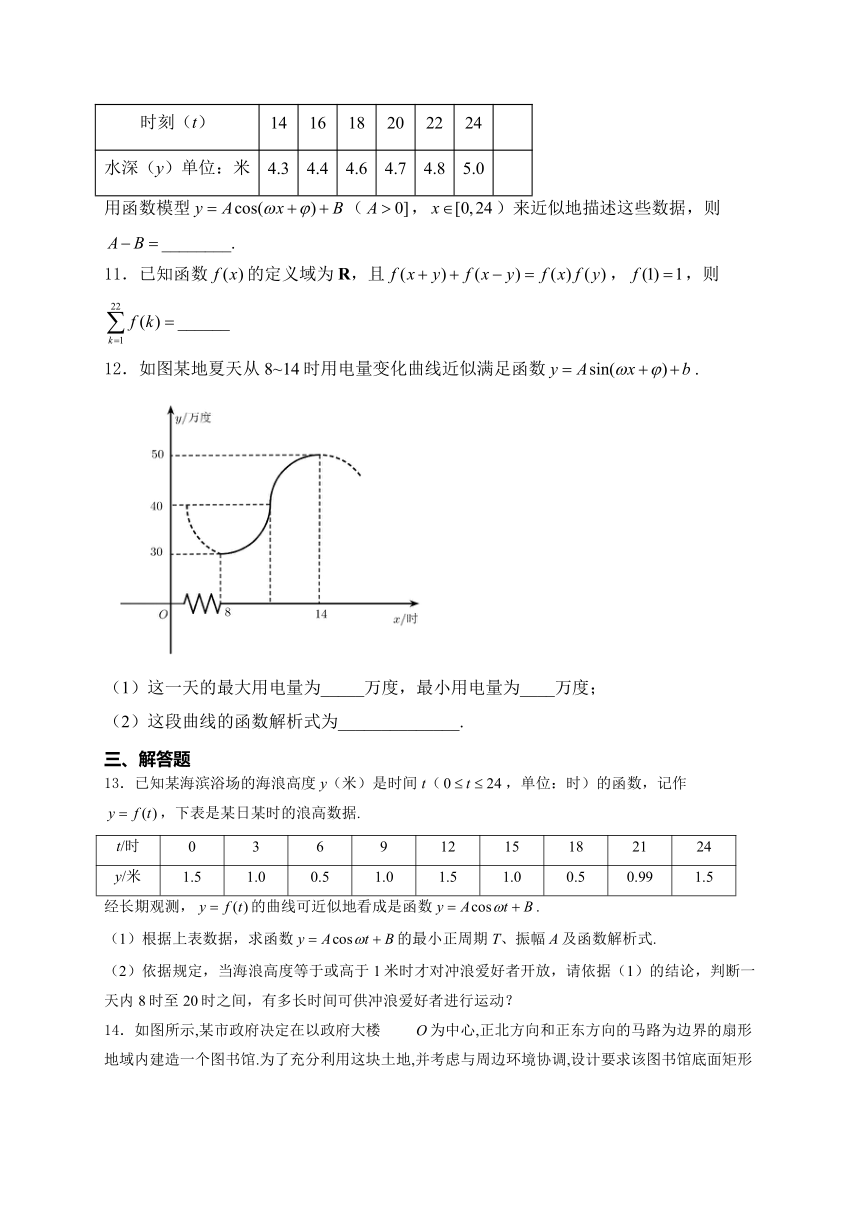
12.如图某地夏天从8~14时用电量变化曲线近似满足函数.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
三、解答题
13.已知某海滨浴场的海浪高度y(米)是时间t(,单位:时)的函数,记作,下表是某日某时的浪高数据.
t/时 0 3 6 9 12 15 18 21 24
y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,的曲线可近似地看成是函数.
(1)根据上表数据,求函数的最小正周期T、振幅A及函数解析式.
(2)依据规定,当海浪高度等于或高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内8时至20时之间,有多长时间可供冲浪爱好者进行运动?
14.如图所示,某市政府决定在以政府大楼 O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形ABCD的四个顶点都要在边界上,图书馆的正面要朝向市政府大楼.设扇形的半径,,OB与OM之间的夹角为.
(1)将图书馆底面矩形ABCD的面积S表示成的函数.
(2)若,求当为何值时,矩形ABCD的面积 S最大 最大面积是多少 (取)
15.心脏跳动时,血压在增加或减少,血压的最大位、最小值分别称为收缩压、舒张压,血压计上的读数就是收缩压、舒张压,读数为标准值.设某人的血压满足.其中为血压,t为时间.
(1)求函数的最小正周期;
(2)求此人每分钟心跳的次数;
(3)画出函数在一个周期内的草图;
(4)求出此人的血压在血压计上的读数,并与标准值进行比较.
16.如图所示为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动角到OB,设B点与地面距离为h.
(1)求h与间关系的函数解析式;
(2)设从OA开始转动,经过t秒到达OB,求h与t间关系的函数解析式.
参考答案
1.答案:B
解析:设P与地面高度与时间t的关系,(,,),
由题意可知:,,,,
即,
又因为,即,故,
,
.
故选B.
2.答案:C
解析:根据题意,当时,函数取得最大值,当时,函数取得最小值因此排除选项A,D;
又当时,函数y是单调递增的,当时,函数y是单调递减的,由此排除选项B;
故选:C.
3.答案:A
解析:由题图知,函数的周期,
所以,将点代入得,故函数解析式为,再将代入函数解析式得.
故选:A.
4.答案:C
解析:由题意得:函数的周期为,
所以频率,
所以此人每分钟心跳的次数为80.
故选:C.
5.答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
6.答案:C
解析:由题图易得,则,.
7.答案:D
解析:由题图知,.,.将代入上式,得,即,由于,可得.当时,,即该天8h的温度大约为13.故选D.
8.答案:B
解析:由题中表格知,
所以,,.
故选B.
9.答案:,
解析:从题图中可以看出,从6~14时的图象是函数的半个周期,
所以,,
又,,
所以,
所以,
又图像过点,
所以,,由题意得,
所以,
故答案为:,.
10.答案:-4.2或
解析:由表中某市码头某一天水深与时间的关系近似为函数(,),从表中数据可知,函数的最大值为5.0,最小值为4.2,所以,解得,,故.
故答案为:-4.2或写成.
11.答案:-3
解析:令,则,即,
,,两式相加,
得,则,
的周期为6,
令,得,由解得,
又,
,
,
,
,
,
,
.
故答案为:-3.
12.答案:(1)50;30
(2),
解析:(1)由图知,最大用电量为50,最小用电量为30.
(2)由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,,,,.
故,.
13.答案:(1)由表中数据知,周期.
由,得.
由,得..
.
(2)..
..
又.
冲浪爱好者从9时到15时,有6小时可进行运动.
解析:
14.答案:
(1) 由题意,可知点M为的中点,所以.
设OM与BC的交点为F,则,
所以,
所以
,.
(2) 因为,所以,
所以当,即时,S有最大值.
.
故当时,矩形ABCD的面积S最大,最大面积为838.35.
解析:
15.答案:(1)由题意,可得,
所以函数的最小正周期为.
(2)函数的频率,
即此人每分钟心跳的次数为80.
(3)列表:
0
115 140 115 90 115
描点、连线得函数在一个周期内的简图如图所示.
(4)此人收缩压为,舒张压为,与标准值相比较,此人血压偏高.
解析:
16.答案:(1)如图,过点O作地面的平行线ON,过点B作ON的垂线BM交ON于点M.
当时,;
当时,上述解析式也适合.
综上所述,.
(2)点A在⊙O上逆时针运动的角速度是.
所以t秒转过的弧度数为,
所以.
解析:
一、选择题
1.某巨型摩天轮.其旋转半径50米,最高点距地面110米,运行一周大约21分钟.某人在最低点的位置坐上摩天轮,则第35分钟时他距地面大约为米.
A.75 B.85 C.100 D.110
2.下表是某市近30年来月平均气温(℃)的数据统计表:
月份 1 2 3 4 5 6 7 8 9 10 11 12
月平均气温 -5.9 -3.3 2.2 9.3 15.1 20.3 22.8 22.2 18.2 11.9 4.3 -2.4
则适合这组数据的函数模型是( )
A.
B.(,)
C.(,)
D.
3.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则t为(秒)时的电流强度为( )
A.0 B. C. D.
4.某人的血压满足函数解析式,其中为血压,t为时间,则此人每分钟心跳的次数为( )
A.60 B.70 C.80 D.90
5.电流强度I(安培)随时间t(秒)变化的函数的图象如图所示,则时的电流强度为( )
A.0安培 B.安培 C.安培 D.安培
6.如图,某港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为( )
A.5 B.6 C.8 D.10
7.甲地某天6h至14h的温度变化曲线如图所示,其近似满足函数,则该天8h的温度大约为( )
A.16 B.15 C.14 D.13
8.已知某帆船中心比赛场馆区的海面上海浪高度:y(米)可看作时间t(,单位:时)的函数,记作,经长期观测, 的曲线可近似地看成是函数的图象,下表是某日各时的浪高数据:
0 3 6 9 12 15 18 21 24
2 1.5 1 1.5 2 1.5 0.99 1.5 2
则最能近似地表示表中数据间对应关系的函数是( )
A. B.
C. D.
二、填空题
9.如图,某地一天从6~14时的温度变化曲线近似满足函数,,则这段曲线的函数解析式为_________.
10.潮汐是发生在沿海地区的一种自然现象,是指海水在天体(主要是月球和太阳)引潮力作用下所产生的周期性运动.习惯上把海面垂直方向涨落称为潮汐,而海水在水平方向的流动称为潮流.早先的人们为了表示生潮的时刻,把发生在早晨的高潮叫潮,发生在晚上的高潮叫汐,这是潮汐名称的由来.下表中给出了某市码头某一天水深与时间的关系(夜间零点开始计时).
时刻(t) 0 2 4 6 8 10 12
水深(y)单位:米 5.0 4.8 4.7 4.6 4.4 4.3 4.2
时刻(t) 14 16 18 20 22 24
水深(y)单位:米 4.3 4.4 4.6 4.7 4.8 5.0
用函数模型(,)来近似地描述这些数据,则________.
11.已知函数的定义域为R,且,,则______
12.如图某地夏天从8~14时用电量变化曲线近似满足函数.
(1)这一天的最大用电量为_____万度,最小用电量为____万度;
(2)这段曲线的函数解析式为______________.
三、解答题
13.已知某海滨浴场的海浪高度y(米)是时间t(,单位:时)的函数,记作,下表是某日某时的浪高数据.
t/时 0 3 6 9 12 15 18 21 24
y/米 1.5 1.0 0.5 1.0 1.5 1.0 0.5 0.99 1.5
经长期观测,的曲线可近似地看成是函数.
(1)根据上表数据,求函数的最小正周期T、振幅A及函数解析式.
(2)依据规定,当海浪高度等于或高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内8时至20时之间,有多长时间可供冲浪爱好者进行运动?
14.如图所示,某市政府决定在以政府大楼 O为中心,正北方向和正东方向的马路为边界的扇形地域内建造一个图书馆.为了充分利用这块土地,并考虑与周边环境协调,设计要求该图书馆底面矩形ABCD的四个顶点都要在边界上,图书馆的正面要朝向市政府大楼.设扇形的半径,,OB与OM之间的夹角为.
(1)将图书馆底面矩形ABCD的面积S表示成的函数.
(2)若,求当为何值时,矩形ABCD的面积 S最大 最大面积是多少 (取)
15.心脏跳动时,血压在增加或减少,血压的最大位、最小值分别称为收缩压、舒张压,血压计上的读数就是收缩压、舒张压,读数为标准值.设某人的血压满足.其中为血压,t为时间.
(1)求函数的最小正周期;
(2)求此人每分钟心跳的次数;
(3)画出函数在一个周期内的草图;
(4)求出此人的血压在血压计上的读数,并与标准值进行比较.
16.如图所示为一个观览车示意图,该观览车半径为4.8m,圆上最低点与地面距离为0.8m,60秒转动一圈,图中OA与地面垂直,以OA为始边,逆时针转动角到OB,设B点与地面距离为h.
(1)求h与间关系的函数解析式;
(2)设从OA开始转动,经过t秒到达OB,求h与t间关系的函数解析式.
参考答案
1.答案:B
解析:设P与地面高度与时间t的关系,(,,),
由题意可知:,,,,
即,
又因为,即,故,
,
.
故选B.
2.答案:C
解析:根据题意,当时,函数取得最大值,当时,函数取得最小值因此排除选项A,D;
又当时,函数y是单调递增的,当时,函数y是单调递减的,由此排除选项B;
故选:C.
3.答案:A
解析:由题图知,函数的周期,
所以,将点代入得,故函数解析式为,再将代入函数解析式得.
故选:A.
4.答案:C
解析:由题意得:函数的周期为,
所以频率,
所以此人每分钟心跳的次数为80.
故选:C.
5.答案:A
解析:由题图知,函数的周期,所以,则,将点代入,可得,,.又,,故函数解析式为,将代入函数解析式,得.
6.答案:C
解析:由题图易得,则,.
7.答案:D
解析:由题图知,.,.将代入上式,得,即,由于,可得.当时,,即该天8h的温度大约为13.故选D.
8.答案:B
解析:由题中表格知,
所以,,.
故选B.
9.答案:,
解析:从题图中可以看出,从6~14时的图象是函数的半个周期,
所以,,
又,,
所以,
所以,
又图像过点,
所以,,由题意得,
所以,
故答案为:,.
10.答案:-4.2或
解析:由表中某市码头某一天水深与时间的关系近似为函数(,),从表中数据可知,函数的最大值为5.0,最小值为4.2,所以,解得,,故.
故答案为:-4.2或写成.
11.答案:-3
解析:令,则,即,
,,两式相加,
得,则,
的周期为6,
令,得,由解得,
又,
,
,
,
,
,
,
.
故答案为:-3.
12.答案:(1)50;30
(2),
解析:(1)由图知,最大用电量为50,最小用电量为30.
(2)由图知,最大用电量为50,最小用电量为30,
故,所以,
又由图象可得半周期为,,故,
又时,,,,,.
故,.
13.答案:(1)由表中数据知,周期.
由,得.
由,得..
.
(2)..
..
又.
冲浪爱好者从9时到15时,有6小时可进行运动.
解析:
14.答案:
(1) 由题意,可知点M为的中点,所以.
设OM与BC的交点为F,则,
所以,
所以
,.
(2) 因为,所以,
所以当,即时,S有最大值.
.
故当时,矩形ABCD的面积S最大,最大面积为838.35.
解析:
15.答案:(1)由题意,可得,
所以函数的最小正周期为.
(2)函数的频率,
即此人每分钟心跳的次数为80.
(3)列表:
0
115 140 115 90 115
描点、连线得函数在一个周期内的简图如图所示.
(4)此人收缩压为,舒张压为,与标准值相比较,此人血压偏高.
解析:
16.答案:(1)如图,过点O作地面的平行线ON,过点B作ON的垂线BM交ON于点M.
当时,;
当时,上述解析式也适合.
综上所述,.
(2)点A在⊙O上逆时针运动的角速度是.
所以t秒转过的弧度数为,
所以.
解析:
