广东省花都区花山初级中学北师大版数学九年级下册课件:3.6直线和圆的关系(1)(共18张PPT)
文档属性
| 名称 | 广东省花都区花山初级中学北师大版数学九年级下册课件:3.6直线和圆的关系(1)(共18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 200.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 10:34:51 | ||
图片预览



文档简介
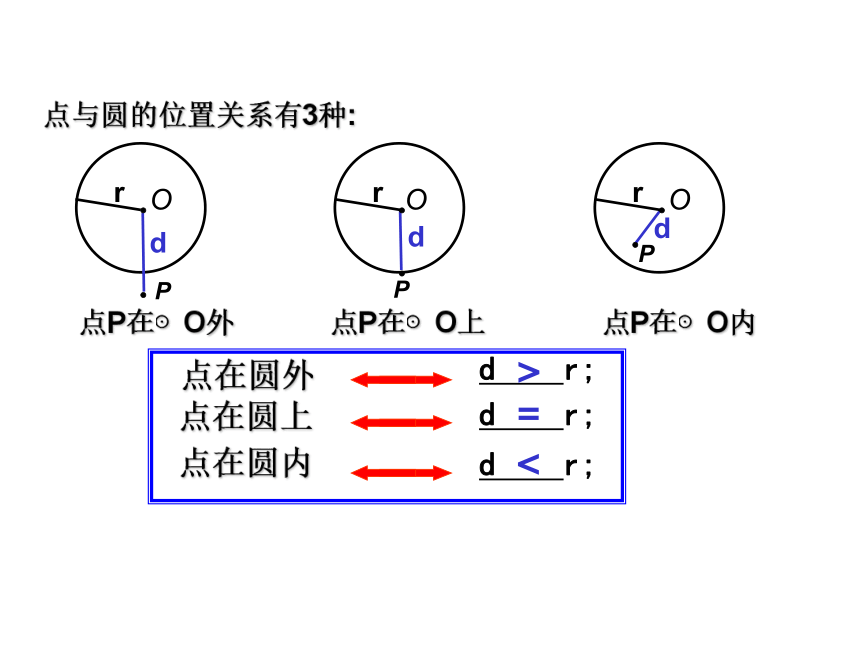
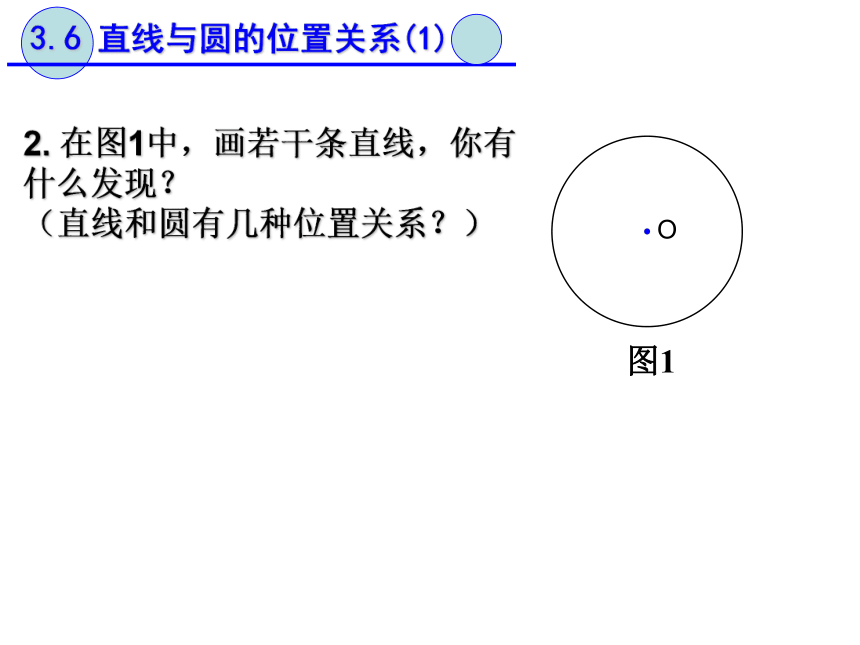
课件18张PPT。1.点与圆的位置关系有哪几种?怎么判定? 点P在⊙O外Od r;d r;d r;>=直线与圆的位置关系又有哪几种呢? 3.5 直线与圆的位置关系(1)3.6 直线与圆的位置关系(1)【学习目标】 (见学案)3.6 直线与圆的位置关系(1)2. 在图1中,画若干条直线,你有什么发现?
(直线和圆有几种位置关系?)
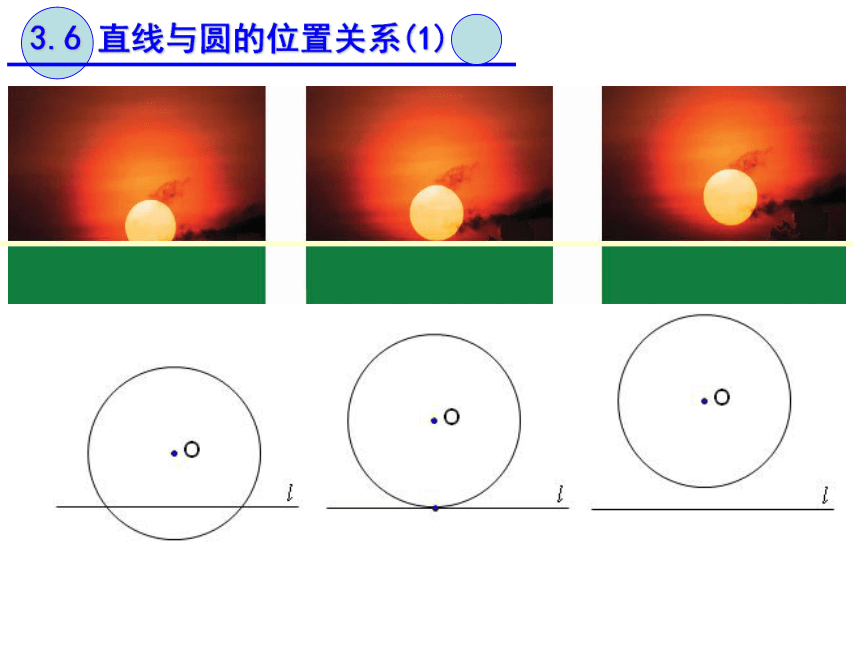
图13.6 直线与圆的位置关系(1)直线和圆的位置关系有3种:______、_____、_____相交相切相离3.6 直线与圆的位置关系(1)2相交1相切0相离这时的直线叫______切线切点直线与圆有唯一____________(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.公共点课本P893.6 直线与圆的位置关系(1)4. 阅读课本P89 想一想
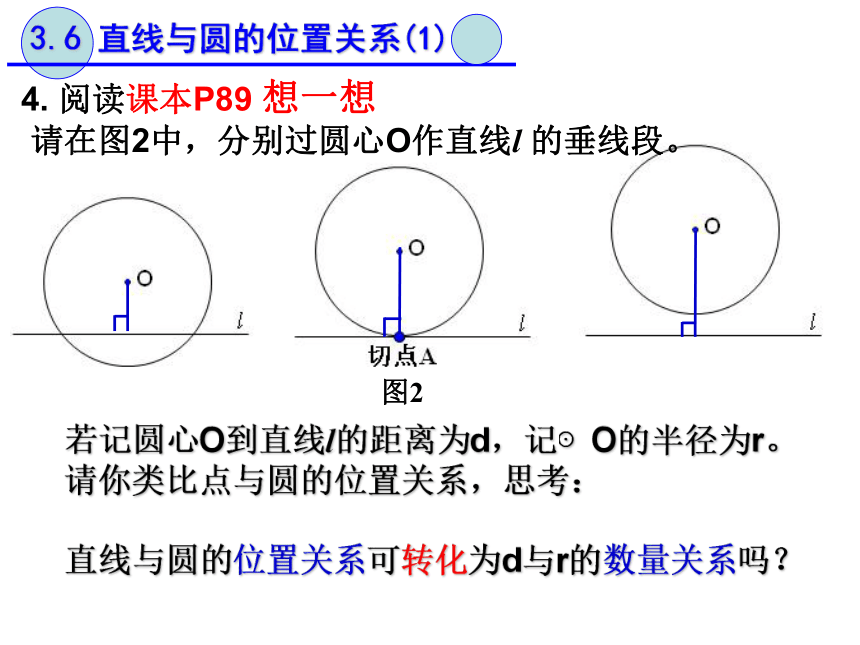
请在图2中,分别过圆心O作直线l 的垂线段。 图2 若记圆心O到直线l的距离为d,记⊙O的半径为r。
请你类比点与圆的位置关系,思考:
直线与圆的位置关系可转化为d与r的数量关系吗? (1)直线与圆相交 d_____r3.6 直线与圆的位置关系(1)(2)直线与圆相切 d_____r(3)直线与圆相离 d_____r直线与圆的位置关系可转化为
直线到圆心的距离d与半径r的数量关系<=> 直线与圆的位置关系和“d与r”的大小(数量)关系
可相互转化。(1)当r=_____时,⊙A与BC(指边BC所在的直线)相切。
(2)当r= 3.4 时,⊙A与BC的位置关系是__________。
3.6 直线与圆的位置关系(1)图3例题讲解:
7.如图3,在Rt△ABC中,∠C=90°,AC=3,BC=4,
以A为圆心,r为半径作圆。
3相交圆心A到直线BC的距离过圆心A到往直线BC作垂线段(1)当r=_____时,⊙C与AB(指边AB所在的直线)相切。
(2)当半径r分别为2和3时,⊙C与AB分别有怎样的位置关系?
3.6 直线与圆的位置关系(1)图4例题讲解:
8.如图4,在Rt△ABC中,∠C=90°,AC=3,BC=4,
以A为圆心,r为半径作圆。
圆心C到直线AB的距离过圆心C到往直线AB作垂线段3.6 直线与圆的位置关系(1)圆的切线_____过切点的半径(直径)。3.6 直线与圆的位置关系(1)2、如图,一枚直径为d的硬币沿着直线滚动一圈,
圆心经过的距离是多少?3.6 直线与圆的位置关系(1)10. 已知⊙O 的半径为3cm,圆心O到直线l的距离为2cm,则直线 l与⊙O的位置关系是___________.
11. 直线l与半径为r的⊙O相交,且O到l的距离为3cm,则r的取值范围是___________.
12.在平面直角坐标系中,以点(2,3)为圆心, 2为半径的圆一定( )
A. 与x轴相离、与y轴相切 B. 与x轴、与y轴都相离
C. 与x轴相切、与y轴相离 D. 与x轴、y轴都相切相交r>3A3.6 直线与圆的位置关系(1)1.在 Rt△ABC中,∠C = 90°, ∠B = 30°, O 是AB 上的一点,OA = m,⊙O 的半径为r,当 r 与 m 满足怎样的关系时,
(1) AC与⊙O 相交? (2)AC与⊙O 相切?
(3) AC 与 ⊙O 相离?
3.6 直线与圆的位置关系(1)3.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出 AB = 6 cm.这张光盘的直径是多少?
3.6 直线与圆的位置关系(1)课堂小结
(1)这节课你学到了什么?
(2)你会判别直线与圆的位置关系吗?你是怎么做的? 直线与圆的位置关系与“d与r”的大小(数量)关系
可相互转化。知道直线与圆的位置关系,可比较“d与r”的数量关系
知道“d与r”的数量关系,可判别直线与圆的位置关系。相交相切相离OOO直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;<=>drdrdr直线与圆的位置关系与直线到圆心的距离
d与半径r的数量关系可相互转化。3.6 直线与圆的位置关系(1)15.某地区准备在相距2千米的A, B工厂间修一条笔直的公路,但在B地北偏东60°方向、A地北偏西45°方向的C处,有一个半径为0.6千米的住宅小区(见下图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: , )
(直线和圆有几种位置关系?)
图13.6 直线与圆的位置关系(1)直线和圆的位置关系有3种:______、_____、_____相交相切相离3.6 直线与圆的位置关系(1)2相交1相切0相离这时的直线叫______切线切点直线与圆有唯一____________(即直线和圆相切)时,这条直线叫做圆的切线,这个唯一的公共点叫做切点.公共点课本P893.6 直线与圆的位置关系(1)4. 阅读课本P89 想一想
请在图2中,分别过圆心O作直线l 的垂线段。 图2 若记圆心O到直线l的距离为d,记⊙O的半径为r。
请你类比点与圆的位置关系,思考:
直线与圆的位置关系可转化为d与r的数量关系吗? (1)直线与圆相交 d_____r3.6 直线与圆的位置关系(1)(2)直线与圆相切 d_____r(3)直线与圆相离 d_____r直线与圆的位置关系可转化为
直线到圆心的距离d与半径r的数量关系<=> 直线与圆的位置关系和“d与r”的大小(数量)关系
可相互转化。(1)当r=_____时,⊙A与BC(指边BC所在的直线)相切。
(2)当r= 3.4 时,⊙A与BC的位置关系是__________。
3.6 直线与圆的位置关系(1)图3例题讲解:
7.如图3,在Rt△ABC中,∠C=90°,AC=3,BC=4,
以A为圆心,r为半径作圆。
3相交圆心A到直线BC的距离过圆心A到往直线BC作垂线段(1)当r=_____时,⊙C与AB(指边AB所在的直线)相切。
(2)当半径r分别为2和3时,⊙C与AB分别有怎样的位置关系?
3.6 直线与圆的位置关系(1)图4例题讲解:
8.如图4,在Rt△ABC中,∠C=90°,AC=3,BC=4,
以A为圆心,r为半径作圆。
圆心C到直线AB的距离过圆心C到往直线AB作垂线段3.6 直线与圆的位置关系(1)圆的切线_____过切点的半径(直径)。3.6 直线与圆的位置关系(1)2、如图,一枚直径为d的硬币沿着直线滚动一圈,
圆心经过的距离是多少?3.6 直线与圆的位置关系(1)10. 已知⊙O 的半径为3cm,圆心O到直线l的距离为2cm,则直线 l与⊙O的位置关系是___________.
11. 直线l与半径为r的⊙O相交,且O到l的距离为3cm,则r的取值范围是___________.
12.在平面直角坐标系中,以点(2,3)为圆心, 2为半径的圆一定( )
A. 与x轴相离、与y轴相切 B. 与x轴、与y轴都相离
C. 与x轴相切、与y轴相离 D. 与x轴、y轴都相切相交r>3A3.6 直线与圆的位置关系(1)1.在 Rt△ABC中,∠C = 90°, ∠B = 30°, O 是AB 上的一点,OA = m,⊙O 的半径为r,当 r 与 m 满足怎样的关系时,
(1) AC与⊙O 相交? (2)AC与⊙O 相切?
(3) AC 与 ⊙O 相离?
3.6 直线与圆的位置关系(1)3.为了测量一个光盘的直径,小明把直尺、光盘和三角尺按图所示放置于桌面上,并量出 AB = 6 cm.这张光盘的直径是多少?
3.6 直线与圆的位置关系(1)课堂小结
(1)这节课你学到了什么?
(2)你会判别直线与圆的位置关系吗?你是怎么做的? 直线与圆的位置关系与“d与r”的大小(数量)关系
可相互转化。知道直线与圆的位置关系,可比较“d与r”的数量关系
知道“d与r”的数量关系,可判别直线与圆的位置关系。相交相切相离OOO直线和圆相交d r;d r; 直线和圆相切 直线和圆相离d r;<=>drdrdr直线与圆的位置关系与直线到圆心的距离
d与半径r的数量关系可相互转化。3.6 直线与圆的位置关系(1)15.某地区准备在相距2千米的A, B工厂间修一条笔直的公路,但在B地北偏东60°方向、A地北偏西45°方向的C处,有一个半径为0.6千米的住宅小区(见下图),问修筑公路时,这个小区是否有居民需要搬迁?(参考数据: , )
