2024-2025学年北京市西城区育才学校八年级(上)期中数学试卷(图片版,无答案)
文档属性
| 名称 | 2024-2025学年北京市西城区育才学校八年级(上)期中数学试卷(图片版,无答案) |  | |
| 格式 | |||
| 文件大小 | 573.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 19:46:13 | ||
图片预览


文档简介
2024-2025 学年度第一学期
北京市育才学校八年级数学学科期中考试试卷
班级: 学号: 姓名:
一、选择题(每题 2分,共 16 分)
1.下面四个图形中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. x3+x3=x6 B. x2 x5 x10 C. (x6 )6 x36 D. (2x2)2=2x4
3. 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画了一个与书上
完全一样的三角形,那么亮亮画图的依据是( )
A. SSS B. ASA C. SAS D. AAS
第 3题图 第 5题图 第 7 题图 第 8 题图
4. 下列说法错.误.的是( )
A. 直角三角形两锐角互余
B. 直角边,斜边分别相等的两个直角三角形全等
C. 如果两个三角形全等,则它们一定是关于某条直线成轴对称
D. 与线段两个端点距离相等的点在这条线段的垂直平分线上
5. 如图,已知△ABC≌△DEF,若∠A=40°,∠DEF=65°,则∠ACB的度数( ).
A.105° B.95° C.75° D.115°
6.若一个多边形的内角和等于 720°,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
7. 如图,战斗机在空中展示的轴对称队形. 以飞机所在直线为 x轴,队形的对称轴为 y轴,
建立平面直角坐标系. 若飞机 E的坐标为(40, a),则飞机 D的坐标为( )
1
A.( 40,-a ) B. ( a,-40 ) C. (-40,-a ) D.(-40, a )
8. 如图,以长方形 ABCD的四条边为边向外作四个正方形,设计出“中”字图案. 若四个正
方形的周长之和为 24,面积之和为 12,则长方形 ABCD的面积为( )
3 8
A.1 B.2 C. D.
2 3
二、填空题(每题 2 分,共 16 分)
9. 在△ABC中,若∠A︰∠B︰∠C=1︰2︰3,则∠A= ,∠B= .
10. 等腰三角形的一边长是 8,另一边长是 5,则周长为 ________________.
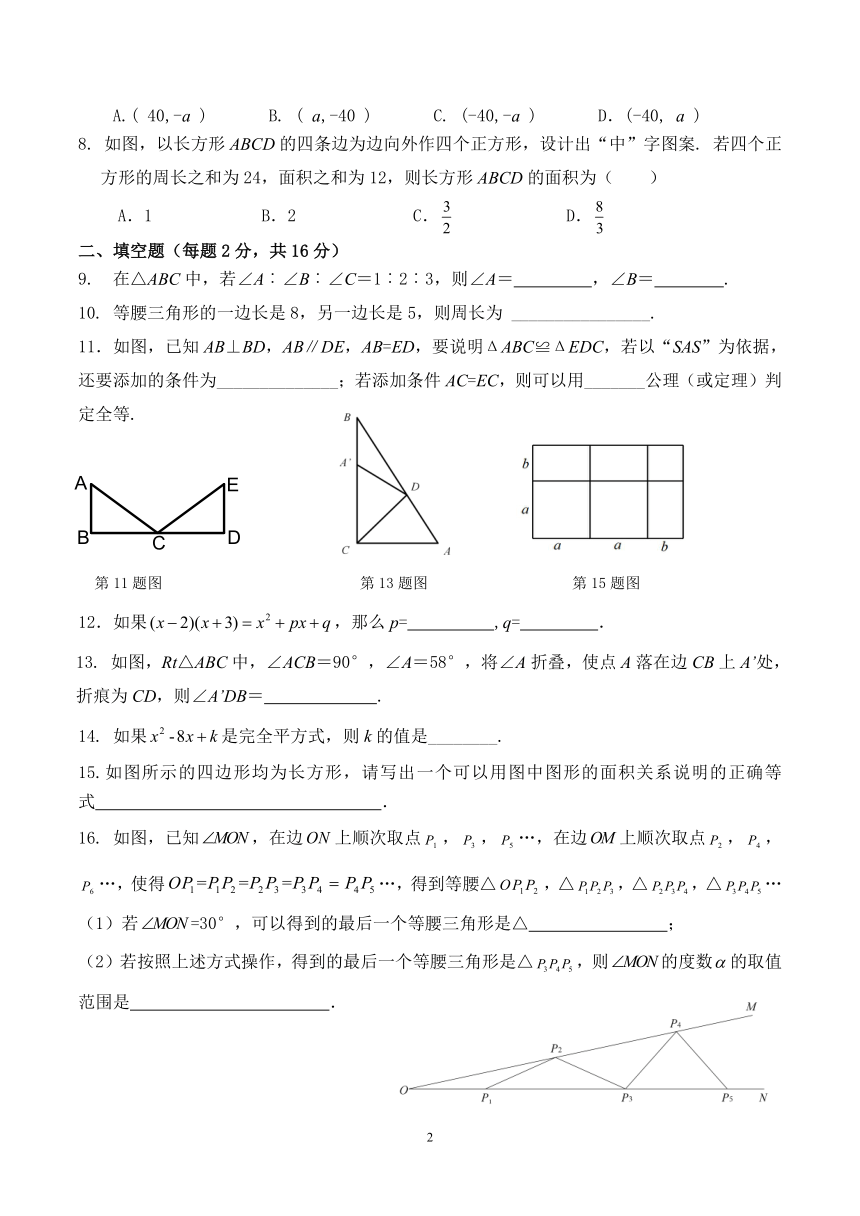
11.如图,已知 AB⊥BD,AB∥DE,AB=ED,要说明ΔABC≌ΔEDC,若以“SAS”为依据,
还要添加的条件为______________;若添加条件 AC=EC,则可以用_______公理(或定理)判
定全等.
A E
B C D
第 11 题图 第 13 题图 第 15 题图
12.如果 (x 2)(x 3) x2 px q,那么 p= ,q= .
13. 如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点 A落在边 CB上 A’处,
折痕为 CD,则∠A’DB= .
14. 如果 x2 -8x k是完全平方式,则 k的值是________.
15.如图所示的四边形均为长方形,请写出一个可以用图中图形的面积关系说明的正确等
式 .
16. 如图,已知 MON,在边ON 上顺次取点 P1 , P3 , P5 …,在边OM上顺次取点 P2 , P4 ,
P6 …,使得OP1=P1P2 =P2P3=P3P4 P4P5 …,得到等腰△OP1P2 ,△ P1P2P3 ,△ P2P3P4,△ P3P4P5 …
(1)若 MON =30°,可以得到的最后一个等腰三角形是△ ;
(2)若按照上述方式操作,得到的最后一个等腰三角形是△ P3P4P5 ,则 MON的度数 的取值
范围是 .
2
三、解答题(共 68 分)
17. 计算 :(每题5分,共 10 分)
(1) ( 2m2 )3 m2 m4 2
(2) (2x 3)(x 4) (x 2)(3x 1)
18. 因式分解:(每题5分,共 10 分)
3
(1) x y xy
3
(2) 2a2b 16ab 32b
19. 6 2 1(本题 分)先化简,再求值: 2x 3y (2x y) 2x y ,其中 x , y 1 .
3
20.(本题 6分)已知:如图,点 A、E、F、C在同一条直线上,DF=BE,∠B=∠D,AD∥BC.
求证:AE=FC.
21. (本题 9 分)如图,已知∠AOB和线段 MN,点 M,N在射线 OA,OB上.
(1)尺规作图:作∠AOB的角平分线和线段 MN的垂直平分线,交于点 P,保留作图痕迹,
不写作图步骤;
(2)连接 MP、NP,过 P作 PC⊥OA,PD⊥OB,垂足分别为点 C和点 D,求证:MC=ND. 请
补全下列证明.
证明: P在线段 MN的垂直平分线上,
MP NP .(______________________________________)
P在∠AOB的角平分线上,PC⊥OA,PD⊥OB,
PC PD .(______________________________________)
请补全后续证明.
3
22.(本题 7分) 如图,在平面直角坐标系 xOy 中,点 A(1,2),B(4,1).
(1)在图中标出点 A,点 B关于 x轴的对称点 A1,B1
的位置,
(2)写出 A1,B1的坐标:A1 ,B1 ;
(3)已知点 C在坐标轴上,且满足△ABC是等腰三角
形,则所有符合条件的点 C有 个, 并写出任意两
个符合条件的点 C的坐标:C1 ,C2 .
23.(本题 8分)如图,已知:△OAB,△EOF都是等腰直角三角形,∠AOB=90°中,∠EOF=90°,
连接 AE、BF.
求证:(1)AE=BF; (2)AE⊥BF.
24. (本题 4 分)如图,在 4 4的网格中有格点三角形,请在下面的图中画出与它成轴对称的
格点三角形,至少画出四个不同的方案,并画.出.对.称.轴..
25. (本题 8分)
(1)如图 1,在△ABC中,点 D为 BC的中点,若 AB=5,AC=3,求 AD的取值范围;
(2)如图 2,在△ABC中,AB=AC,AB⊥AC,点 D是线段 BC上一动点,点 F为 BD的中点,
AD=AE且 AD⊥AE,求 AF与 EC的数量关系,并说明理由;
(3)如图 3,在△ABC中,AB=AC,点 D是△ABC内一点,点 E是 BD的中点,连 AE,作
AE⊥EF,若 DF=CF,直接写出∠BAC与∠DFC之间的关系是 .
4
图 1 图 2 图 3
四、选做题(共 10 分)
26. (本题 4分)观察下列等式:
1 1
①1 1 ;
2 1 2
1 1 1 1
② ;
2 3 4 3 4
1 1 1 1
③ ;
3 5 6 5 6
1 1 1 1
④ ;
4 7 8 7 8
……
根据上述规律回答下列问题:
(1)第⑤个等式是 ;
(2)第 n个等式是 (用含 n的式子表示,n为正整数).
27. (本题 6分)在平面直角坐标系 xOy中,点 P,Q分别在线段 OA,OB上.如果存在点 M
使得 MP=MQ ,∠MPQ=∠AOB(M,P,Q逆时针排列),则称点 M是线段 PQ的“关联点”.
如图1,点 M是线段 PQ的“关联点”.
(1)如图2,已知点 A(4,4),B(8,0),点 P与点 A重合.
① 当点 Q是线段 OB中点时,在M1(4,2),M 2(6,2)中,其中是线段 PQ的“关联点”
的是 ;
② 已知点 M(8,4)是线段 PQ的“关联点”,则点 Q的坐标是 .
(2)如图 3,已知 OA=OB=4,∠AOB=60°.
①当点 P与点 A重合,点 Q在线段 OB上运动时(点 Q不与点 O重合),若点 M是线段
PQ的“关联点”,求证:BM∥OA;
5
②当点 P,Q分别在线段 OA,OB上运动时,直接写出线段 PQ的“关联点” M形成
的区域的周长.
6
北京市育才学校八年级数学学科期中考试试卷
班级: 学号: 姓名:
一、选择题(每题 2分,共 16 分)
1.下面四个图形中,是轴对称图形的是( )
A. B. C. D.
2. 下列运算正确的是( )
A. x3+x3=x6 B. x2 x5 x10 C. (x6 )6 x36 D. (2x2)2=2x4
3. 如图,亮亮书上的三角形被墨迹污染了一部分,他根据所学的知识很快就画了一个与书上
完全一样的三角形,那么亮亮画图的依据是( )
A. SSS B. ASA C. SAS D. AAS
第 3题图 第 5题图 第 7 题图 第 8 题图
4. 下列说法错.误.的是( )
A. 直角三角形两锐角互余
B. 直角边,斜边分别相等的两个直角三角形全等
C. 如果两个三角形全等,则它们一定是关于某条直线成轴对称
D. 与线段两个端点距离相等的点在这条线段的垂直平分线上
5. 如图,已知△ABC≌△DEF,若∠A=40°,∠DEF=65°,则∠ACB的度数( ).
A.105° B.95° C.75° D.115°
6.若一个多边形的内角和等于 720°,则这个多边形的边数是( )
A.5 B.6 C.7 D.8
7. 如图,战斗机在空中展示的轴对称队形. 以飞机所在直线为 x轴,队形的对称轴为 y轴,
建立平面直角坐标系. 若飞机 E的坐标为(40, a),则飞机 D的坐标为( )
1
A.( 40,-a ) B. ( a,-40 ) C. (-40,-a ) D.(-40, a )
8. 如图,以长方形 ABCD的四条边为边向外作四个正方形,设计出“中”字图案. 若四个正
方形的周长之和为 24,面积之和为 12,则长方形 ABCD的面积为( )
3 8
A.1 B.2 C. D.
2 3
二、填空题(每题 2 分,共 16 分)
9. 在△ABC中,若∠A︰∠B︰∠C=1︰2︰3,则∠A= ,∠B= .
10. 等腰三角形的一边长是 8,另一边长是 5,则周长为 ________________.
11.如图,已知 AB⊥BD,AB∥DE,AB=ED,要说明ΔABC≌ΔEDC,若以“SAS”为依据,
还要添加的条件为______________;若添加条件 AC=EC,则可以用_______公理(或定理)判
定全等.
A E
B C D
第 11 题图 第 13 题图 第 15 题图
12.如果 (x 2)(x 3) x2 px q,那么 p= ,q= .
13. 如图,Rt△ABC中,∠ACB=90°,∠A=58°,将∠A折叠,使点 A落在边 CB上 A’处,
折痕为 CD,则∠A’DB= .
14. 如果 x2 -8x k是完全平方式,则 k的值是________.
15.如图所示的四边形均为长方形,请写出一个可以用图中图形的面积关系说明的正确等
式 .
16. 如图,已知 MON,在边ON 上顺次取点 P1 , P3 , P5 …,在边OM上顺次取点 P2 , P4 ,
P6 …,使得OP1=P1P2 =P2P3=P3P4 P4P5 …,得到等腰△OP1P2 ,△ P1P2P3 ,△ P2P3P4,△ P3P4P5 …
(1)若 MON =30°,可以得到的最后一个等腰三角形是△ ;
(2)若按照上述方式操作,得到的最后一个等腰三角形是△ P3P4P5 ,则 MON的度数 的取值
范围是 .
2
三、解答题(共 68 分)
17. 计算 :(每题5分,共 10 分)
(1) ( 2m2 )3 m2 m4 2
(2) (2x 3)(x 4) (x 2)(3x 1)
18. 因式分解:(每题5分,共 10 分)
3
(1) x y xy
3
(2) 2a2b 16ab 32b
19. 6 2 1(本题 分)先化简,再求值: 2x 3y (2x y) 2x y ,其中 x , y 1 .
3
20.(本题 6分)已知:如图,点 A、E、F、C在同一条直线上,DF=BE,∠B=∠D,AD∥BC.
求证:AE=FC.
21. (本题 9 分)如图,已知∠AOB和线段 MN,点 M,N在射线 OA,OB上.
(1)尺规作图:作∠AOB的角平分线和线段 MN的垂直平分线,交于点 P,保留作图痕迹,
不写作图步骤;
(2)连接 MP、NP,过 P作 PC⊥OA,PD⊥OB,垂足分别为点 C和点 D,求证:MC=ND. 请
补全下列证明.
证明: P在线段 MN的垂直平分线上,
MP NP .(______________________________________)
P在∠AOB的角平分线上,PC⊥OA,PD⊥OB,
PC PD .(______________________________________)
请补全后续证明.
3
22.(本题 7分) 如图,在平面直角坐标系 xOy 中,点 A(1,2),B(4,1).
(1)在图中标出点 A,点 B关于 x轴的对称点 A1,B1
的位置,
(2)写出 A1,B1的坐标:A1 ,B1 ;
(3)已知点 C在坐标轴上,且满足△ABC是等腰三角
形,则所有符合条件的点 C有 个, 并写出任意两
个符合条件的点 C的坐标:C1 ,C2 .
23.(本题 8分)如图,已知:△OAB,△EOF都是等腰直角三角形,∠AOB=90°中,∠EOF=90°,
连接 AE、BF.
求证:(1)AE=BF; (2)AE⊥BF.
24. (本题 4 分)如图,在 4 4的网格中有格点三角形,请在下面的图中画出与它成轴对称的
格点三角形,至少画出四个不同的方案,并画.出.对.称.轴..
25. (本题 8分)
(1)如图 1,在△ABC中,点 D为 BC的中点,若 AB=5,AC=3,求 AD的取值范围;
(2)如图 2,在△ABC中,AB=AC,AB⊥AC,点 D是线段 BC上一动点,点 F为 BD的中点,
AD=AE且 AD⊥AE,求 AF与 EC的数量关系,并说明理由;
(3)如图 3,在△ABC中,AB=AC,点 D是△ABC内一点,点 E是 BD的中点,连 AE,作
AE⊥EF,若 DF=CF,直接写出∠BAC与∠DFC之间的关系是 .
4
图 1 图 2 图 3
四、选做题(共 10 分)
26. (本题 4分)观察下列等式:
1 1
①1 1 ;
2 1 2
1 1 1 1
② ;
2 3 4 3 4
1 1 1 1
③ ;
3 5 6 5 6
1 1 1 1
④ ;
4 7 8 7 8
……
根据上述规律回答下列问题:
(1)第⑤个等式是 ;
(2)第 n个等式是 (用含 n的式子表示,n为正整数).
27. (本题 6分)在平面直角坐标系 xOy中,点 P,Q分别在线段 OA,OB上.如果存在点 M
使得 MP=MQ ,∠MPQ=∠AOB(M,P,Q逆时针排列),则称点 M是线段 PQ的“关联点”.
如图1,点 M是线段 PQ的“关联点”.
(1)如图2,已知点 A(4,4),B(8,0),点 P与点 A重合.
① 当点 Q是线段 OB中点时,在M1(4,2),M 2(6,2)中,其中是线段 PQ的“关联点”
的是 ;
② 已知点 M(8,4)是线段 PQ的“关联点”,则点 Q的坐标是 .
(2)如图 3,已知 OA=OB=4,∠AOB=60°.
①当点 P与点 A重合,点 Q在线段 OB上运动时(点 Q不与点 O重合),若点 M是线段
PQ的“关联点”,求证:BM∥OA;
5
②当点 P,Q分别在线段 OA,OB上运动时,直接写出线段 PQ的“关联点” M形成
的区域的周长.
6
同课章节目录
