武威第十二中学人教版九年级数学下册26.1反比例函数的图象与性质课件(共18张PPT)
文档属性
| 名称 | 武威第十二中学人教版九年级数学下册26.1反比例函数的图象与性质课件(共18张PPT) | 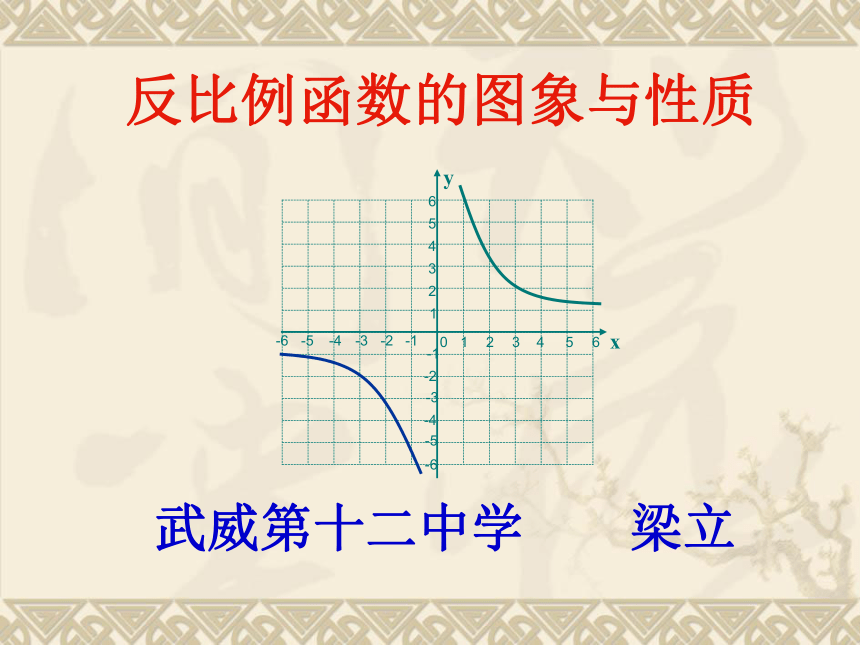 | |
| 格式 | zip | ||
| 文件大小 | 504.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 14:10:19 | ||
图片预览




文档简介
课件18张PPT。武威第十二中学 梁立反比例函数的图象与性质“预见性”,猜一猜反比例函数的图象又会是什么样子呢?你还记得作函数图象的一般步骤吗?给反比例函数“照相”用图象法表示函数关系时,首先在自变量的取值范围内取一些值,列表,描点,连线
(按自变量从小到大的顺序,用一条平滑的曲线连接起来). 函数图象画法列
表描
点连
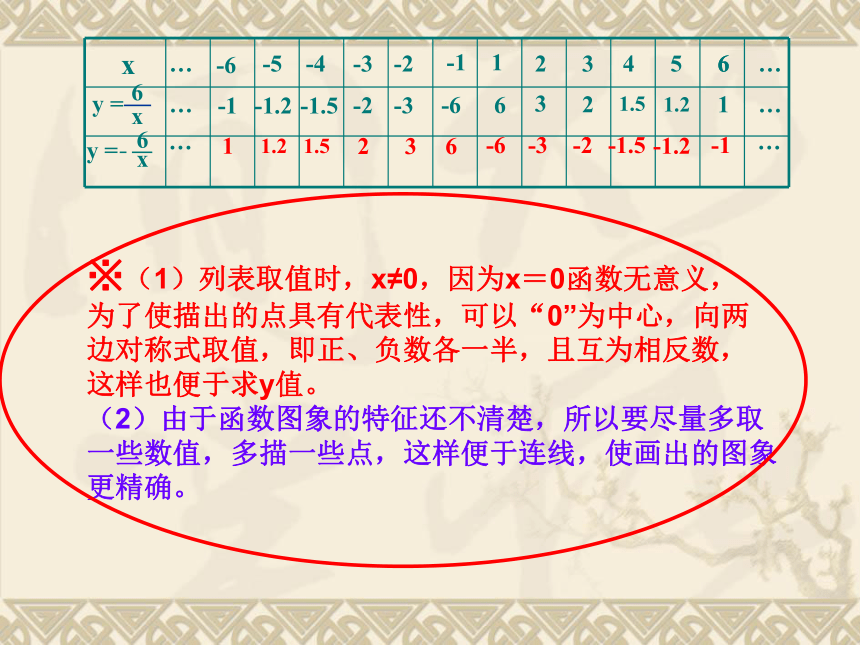
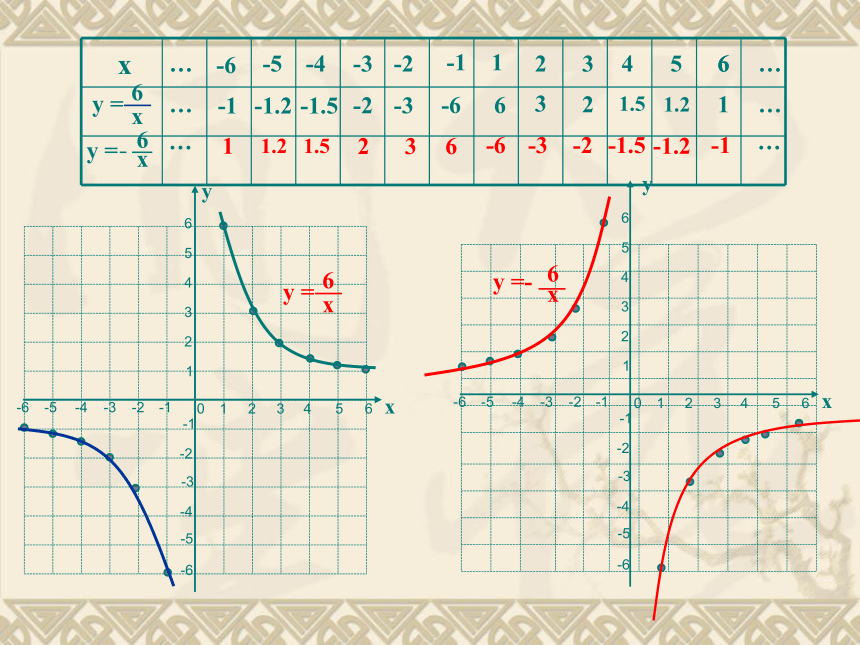
线 描点法例 116233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……※(1)列表取值时,x≠0,因为x=0函数无意义,
为了使描出的点具有代表性,可以“0”为中心,向两
边对称式取值,即正、负数各一半,且互为相反数,
这样也便于求y值。
(2)由于函数图象的特征还不清楚,所以要尽量多取
一些数值,多描一些点,这样便于连线,使画出的图象
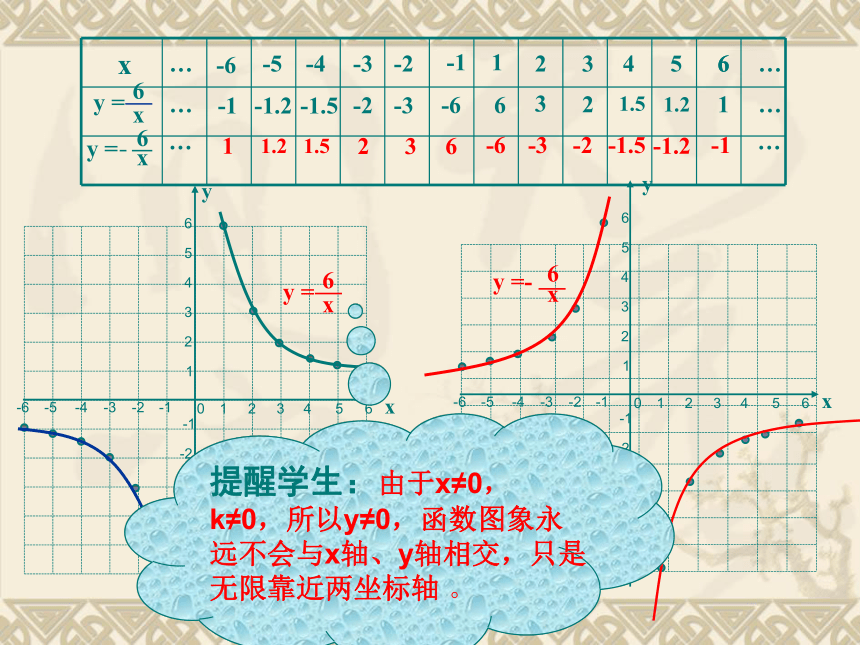
更精确。123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……提醒学生:由于x≠0,
k≠0,所以y≠0,函数图象永
远不会与x轴、y轴相交,只是
无限靠近两坐标轴 。
比较 与 两个图象,它们有什
么共同特点?它们之间有什么关系?
活动二、模拟画图请模拟例1,在同
一平面直角坐标系
中画出反比例函数
与
的函数图像。安排两个学生上台展示,老师应关注:
(1)学生是否熟练地利用描点方法画出反比例函数图象;
(2)学生能否使用反比例函数的对称性,找出比较快捷的画图方法。活动三、归纳新知思考 观察反比例函数,
与 ,以及 , 的函数图象,回答下列问题: 1、你能发现它们的共同特征以及不同点吗?2、每个函数的图象分别位于那个象限?函数图象的位置有谁决定?3、在每一个象限内,y随x的变化如何变化?位置增减性位置增减性y=kx ( k≠0 ) 直线一、三象限从左到右上升
y随x的增大而增大二、四象限 从左到右下降
y随x的增大而减小反比例函数? 双曲线一、三象限在每个象限内
y随x的增大而减小二、四象限在每个象限内
y随x的增大而增大0000xyyyyxxx一、正比例函数和反比例函数的比较我学我用基础训练请指出下面的图像中那一个是反比例函数的图像(C) (A)y=5x
(B)y=2x+3
(C)
(D)2、如图,这是下列四个函数中哪一个函数的图象( C )函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小3、认真填一填 (基础题)1、已知反比例函数
若函数的图象位于第一、三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 4变式练习2、 反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C(中档题)1﹑已知 k<0, 函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )xkyD思前想后 (综合题) 2 函数y=kx-k 与 在同一个直角坐标系中的 图象可能是 :D这是反比例函数及一次函数的性质的综合运用,可以采用
排除法;也可以让学生分两种情况(k>0和k<0)讨论。
我说收获
对同学说你有什么收获:
1、知识
2、思想方法
结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.作业:
习题26.1 必做题 第3、5、6 题
选做题 第8 题
(按自变量从小到大的顺序,用一条平滑的曲线连接起来). 函数图象画法列
表描
点连
线 描点法例 116233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……※(1)列表取值时,x≠0,因为x=0函数无意义,
为了使描出的点具有代表性,可以“0”为中心,向两
边对称式取值,即正、负数各一半,且互为相反数,
这样也便于求y值。
(2)由于函数图象的特征还不清楚,所以要尽量多取
一些数值,多描一些点,这样便于连线,使画出的图象
更精确。123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……123456-1-3-2-4-5-61234-1-2-3-40-6-556yx123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………-663-32-21.5-1.51.2-1.21-1……提醒学生:由于x≠0,
k≠0,所以y≠0,函数图象永
远不会与x轴、y轴相交,只是
无限靠近两坐标轴 。
比较 与 两个图象,它们有什
么共同特点?它们之间有什么关系?
活动二、模拟画图请模拟例1,在同
一平面直角坐标系
中画出反比例函数
与
的函数图像。安排两个学生上台展示,老师应关注:
(1)学生是否熟练地利用描点方法画出反比例函数图象;
(2)学生能否使用反比例函数的对称性,找出比较快捷的画图方法。活动三、归纳新知思考 观察反比例函数,
与 ,以及 , 的函数图象,回答下列问题: 1、你能发现它们的共同特征以及不同点吗?2、每个函数的图象分别位于那个象限?函数图象的位置有谁决定?3、在每一个象限内,y随x的变化如何变化?位置增减性位置增减性y=kx ( k≠0 ) 直线一、三象限从左到右上升
y随x的增大而增大二、四象限 从左到右下降
y随x的增大而减小反比例函数? 双曲线一、三象限在每个象限内
y随x的增大而减小二、四象限在每个象限内
y随x的增大而增大0000xyyyyxxx一、正比例函数和反比例函数的比较我学我用基础训练请指出下面的图像中那一个是反比例函数的图像(C) (A)y=5x
(B)y=2x+3
(C)
(D)2、如图,这是下列四个函数中哪一个函数的图象( C )函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 的图象在第________象限,
在每一象限内,y 随x 的增大而_________.
函数 ,当x>0时,图象在第____象限,
y随x 的增大而_________.
一、三二、四一减小增大减小3、认真填一填 (基础题)1、已知反比例函数
若函数的图象位于第一、三象限, 则k______;
若在每一象限内,y随x增大而增大, 则k______.< 4> 4变式练习2、 反比例函数 (K为常数)图象位于( )
A.第一、二象限 B.第一、三象限
C.第二、四象限 D.第三、四象限C(中档题)1﹑已知 k<0, 函数 y1=kx, y2= 在同一坐标系中的图象大致是 ( )xkyD思前想后 (综合题) 2 函数y=kx-k 与 在同一个直角坐标系中的 图象可能是 :D这是反比例函数及一次函数的性质的综合运用,可以采用
排除法;也可以让学生分两种情况(k>0和k<0)讨论。
我说收获
对同学说你有什么收获:
1、知识
2、思想方法
结束寄语函数来自现实生活,函数是描述现实世界变化规律的重要数学模型.
函数的思想是一种重要的数学思想,它是刻画两个变量之间关系的重要手段.作业:
习题26.1 必做题 第3、5、6 题
选做题 第8 题
