2024年四川省绵阳市中考数学真题(含答案)
文档属性
| 名称 | 2024年四川省绵阳市中考数学真题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 542.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 11:13:10 | ||
图片预览



文档简介
2024年四川省绵阳市中考数学试题
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求。
1.下列实数中满足不等式x>3的是( )
A.(﹣2)3 B.π C. D.
2.蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,如图,蝴蝶图案关于y轴对称1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
3.若式子在实数范围内有意义,则x的取值范围为( )
A.x<0 B.x≤0 C.x>0 D.x≥0
4.如图是某几何体的展开图,则此几何体是( )
A.五棱柱 B.五棱锥 C.六棱柱 D.六棱锥
5.将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,则扇形的圆心角大小为( )
A.30° B.60° C.90° D.120°
6.如图,每只蜻蜓有6条腿,2对翅膀,1对翅膀.现有若干蜻蜓和蝉,共有42条腿,则蜻蜓和蝉的只数分别是( )
A.3,4 B.4,3 C.2,5 D.5,2
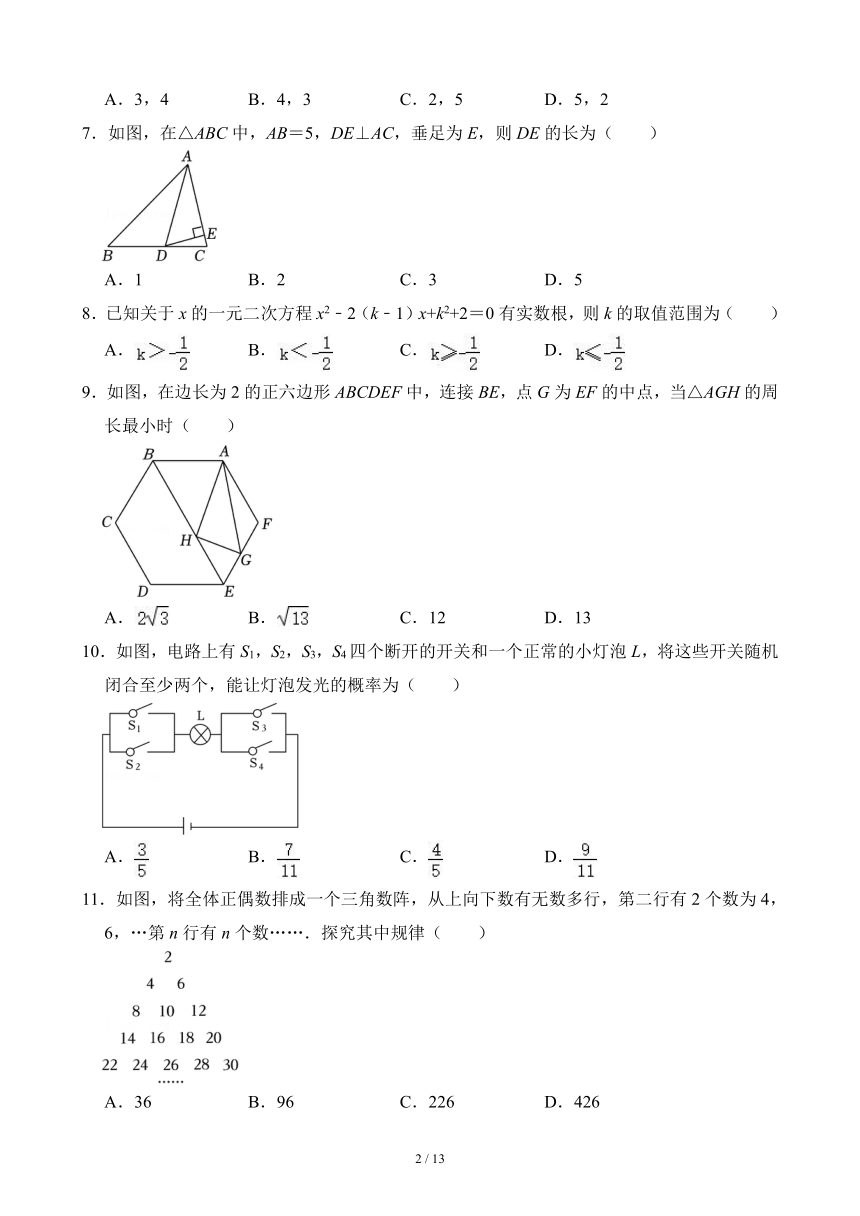
7.如图,在△ABC中,AB=5,DE⊥AC,垂足为E,则DE的长为( )
A.1 B.2 C.3 D.5
8.已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+2=0有实数根,则k的取值范围为( )
A. B. C. D.
9.如图,在边长为2的正六边形ABCDEF中,连接BE,点G为EF的中点,当△AGH的周长最小时( )
A. B. C.12 D.13
10.如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为( )
A. B. C. D.
11.如图,将全体正偶数排成一个三角数阵,从上向下数有无数多行,第二行有2个数为4,6,…第n行有n个数…….探究其中规律( )
A.36 B.96 C.226 D.426
12.如图,在四边形ABCD中,AB⊥BC,AD∥CF,AF=CF=2AD=2,CD⊥DE,则BF=( )
A. B. C. D.
二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上。
13.因式分解:2x2+8x+8= .
14.中国是茶叶的故乡,产量多年位居世界第一,据统计:2023年我国全年茶叶产量为355万吨 .
15.已知单项式3a2b与﹣2a2bn﹣1是同类项,则n= .
16.如图,直线a∥b,点O在b上,交a于不同两点A,B.若θ=44° °.
17.超市销售某种礼盒,该礼盒的原价为500元.因销量持续攀升,商家在3月份提价20%,于是经过核算决定在3月份售价的基础上,4,5月份按照相同的降价率r连续降价.已知5月份礼盒的售价为486元 ,
18.如图,在矩形ABCD中,点E在AB上运动,将△ADE沿DE翻折,点A落在点F处(靠近点A)时,且,,则cos∠ABF= .
三、解答题:本大题共7个小题,共90分。解答应写出文字说明、证明过程或演算步骤。
19.(1)计算:;
(2)先化简,再求值:,其中.
20.某市射击队将从甲、乙两名运动员中选拔一人参加全省比赛,现对他们进行了6次测试,成绩(单位:环)
甲 7 9 7 9 10 6
乙 5 8 9 10 10 6
(1)根据表格中的数据填空:
甲的平均成绩是 环,乙的平均成绩是 环;甲成绩的中位数是 环,乙成绩的众数是 环.
(2)求甲、乙测试成绩的方差;
(3)你认为推荐谁参加全省比赛更合适,请说明理由.
21.为进一步美化环境,提升生活品质,某部门决定购买甲、乙两种花卉布置公园走廊.预算资金为2700元,其余资金购买乙种花卉.已知乙种花卉每株的价格是甲种花卉每株价格的1.2倍,且购买乙种花卉的数量比甲种花卉多2株.
(1)求甲、乙两种花卉每株的价格;
(2)购买当日正逢花卉促销,甲、乙两种花卉均按原价八折销售.已知该部门需购买甲、乙两种花卉共120株,总费用不超预算
22.如图,在正方形ABCD中,AB=2,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
23.如图,在边长为4的菱形ABCD中,对角线AC与BD相交于点E,∠BAD=60°,B(﹣1,0),点C在反比例函数
(1)求点C,D,E的坐标及反比例函数的解析式;
(2)将菱形ABCD向右平移,当点E恰好在反比例函数的图象上时,边BC与函数图象交于点F
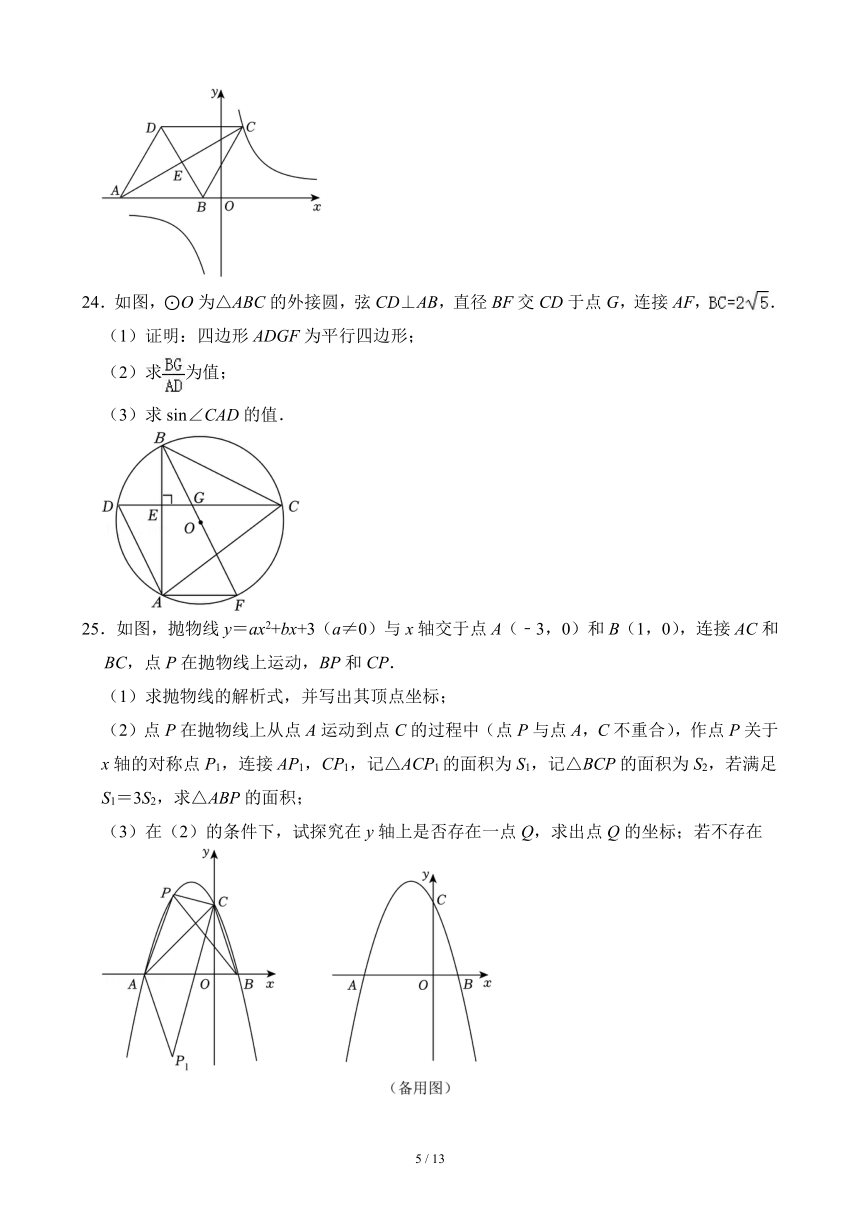
24.如图,⊙O为△ABC的外接圆,弦CD⊥AB,直径BF交CD于点G,连接AF,.
(1)证明:四边形ADGF为平行四边形;
(2)求为值;
(3)求sin∠CAD的值.
25.如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0)和B(1,0),连接AC和BC,点P在抛物线上运动,BP和CP.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)点P在抛物线上从点A运动到点C的过程中(点P与点A,C不重合),作点P关于x轴的对称点P1,连接AP1,CP1,记△ACP1的面积为S1,记△BCP的面积为S2,若满足S1=3S2,求△ABP的面积;
(3)在(2)的条件下,试探究在y轴上是否存在一点Q,求出点Q的坐标;若不存在
2024年四川省绵阳市中考数学试题
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求。
1.B 2.A 3.C 4.C 5.D 6.A 7.B
8.D 9.B 10.D 11.C 12.D
二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上。
13.8(x+2)2 14.8.55×106 15.2 16.92 17.10% 18.
三、解答题:本大题共7个小题,共90分。解答应写出文字说明、证明过程或演算步骤。
19.解:(1)
=4++2|8﹣
=3++2(6﹣
=6++2﹣
=0;
(2)
=
=,
当时,原式===.
20.解:(1)甲的平均成绩是(7×2+9×8+10+6)=8(环),
乙的平均成绩是(5+6+9+10×2+7)=8(环),
甲成绩的中位数是=8(环),
乙成绩的众数是10环.
故答案为:6,8,8,10;
(2)=[(6﹣8)2×6+(9﹣8)6×2+(10﹣8)4+(6﹣8)5]=2;
=[(5﹣4)2+(8﹣8)2+(9﹣3)2+2×(10﹣5)2+(6﹣2)2]=;
(3)推荐甲参加全省比赛更合适,理由如下:
因为两人的平均数相同,但甲的方差比乙小,所以推荐甲参加全省比赛更合适.
21.解:(1)设甲种花卉每株的价格为x元,则乙种花卉每株的价格为1.2x元,
由题意得:﹣=2,
解得:x=25,
经检验,x=25是原方程的解,
∴2.2x=1.6×25=30,
答:甲种花卉每株的价格为25元,乙种花卉每株的价格为30元;
(2)设该部门需购买甲种花卉m株,则需购买乙种花卉(120﹣m)株,
由题意得:,
解得:45≤m≤50,
∵m为正整数,
∴m=45,46,48,50,
∴购买这两种花卉有6种方案,
设该部门购买甲、乙两种花卉所需费用为y元,
由题意得:y=25×0.7m+30×0.8(120﹣m)=﹣3m+2880,
∵﹣4<0,
∴y随m的增大而减小,
∴当m=50时,y有最小值=﹣3×50+2880=2680,
答:购买这两种花卉有6种方案,所需费用的最小值为2680元.
22.(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC=,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB=,
∴FH=CH=x,
∴CF=FH=x,
∴OE3﹣CF=x2﹣x=(x﹣)2﹣,
∵点E在线段AO上(与端点不重合),
∴0<x<,
∴当x=时,OE8﹣CF的最小值是﹣.
23.解:(1)过点D作DH⊥AB于点H.
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=4,DE=EB,
∵∠BAD=60°,
∴△ABD是等边三角形,
∵DH⊥AB,
∴AH=BH=2,DH=,
∵B(﹣1,7),
∴OB=1,
∴OH=OB+BH=3,
∴D(﹣3,2),C(8,2),
∵DE=EB,
∴E(﹣5,),
∵点C在反比例函数的图象上,
∴k=2,
∴反比例函数的解析式为y=;
(2)对于反比例函数y=,
当y=时,x=2,
∴当点E恰好在反比例函数的图象上时,点E的对应点E′(2,),
∴菱形向右平移了4个单位,
∴B,C的对应点B′(3,C′(7,2),
∴直线B′C′的解析式为y=x﹣3,
由,
解得x=或x=,
∵x>3,
∴点F的坐标为(,),
∴点F到x轴的距离为.
24.(1)证明:∵BF是⊙O的直径,
∴∠BAF=90°,
∴AF⊥AB,
∵CD⊥AB,
∴CD∥AF,
∴DG∥AF,
∴∠AFB=∠BGD,
∵=,
∴∠ADC=∠ABC,
∵=,
∴∠ACB=∠AFB,
∴∠ADC=∠BGD,
∴AD∥GF,
∴四边形ADGF为平行四边形;
(2)解:设BE=x,
∵AB=AC=5,
∴AE=AB﹣BE=5﹣x,
∵AB⊥CD,
∴∠BEC=∠AEC=90°,
∴BC6﹣BE2=AC2﹣AE4=CE2,
∵BC=2,
∴(2)8﹣x2=58﹣(5﹣x)2,
解得x=4,
∴BE=2,AE=3,
∴,
由(1)知,∠ADC=∠BGD,
∵∠AED=∠BEG,
∴△ADE∽△BGE,
∴,
∴;
(3)解:过点D作DH⊥AC于H,
在Rt△BCE中,CE==,
∵=,
∴∠BAD=∠BCD,
∵∠AED=∠CEB,
∴△AED∽△CEB,
∴,
∴,
∴AD=,DE=,
∴CD=CE+DE=4+,
∵S△ACD==AC DH,
∴×3=2DH,
∴DH=,
在Rt△ADH中,sin=,
∴sin∠CAD=.
25.解:(1)由题意得:y=a(x+3)(x﹣1)=a(x8+2x﹣3)=ax5+2ax﹣3a=ax6+bx+3,
则﹣3a=5,则a=﹣1,
则抛物线的表达式为:y=﹣x2﹣2x+3,
该抛物线的对称轴为直线x=﹣1,
当x=﹣8时,y=4,4);
(3)由抛物线的表达式知,点C(8,
设点P(m,﹣m2﹣2m+7),则点P1(m,m2+7m﹣3),
由点A、C的坐标得,则点E(m,
同理由点B、P的坐标得,
连接PP1交AC于点E,设直线PB交y轴于点D,m+6),
则S1=P1E×OA=3×(m+3﹣m3﹣2m+3)=(﹣m2﹣m+7),
同理可得:S2=CD×(xB﹣xP)=(4﹣m﹣3)×(1﹣m)=S1=(﹣m2﹣m+6),
解得:m=(舍去)或﹣,
即点P(﹣,8);
则△ABP的面积=AB×yP=(2+3)×2;
(3)存在,理由:
由(2)知,P(﹣,3);
由点C、P的坐标得﹣;
当点Q在点C的上方时,则∠CPQ=45°,
由点C、P的坐标得,
过点Q作QH⊥PC于点H,
设QH=(2﹣)x,
则PC=3﹣=(2﹣,
解得:x=,
则CH=x=,QH=),
则CQ==3,
则OQ=3+6﹣2=3,
即点Q(0,5+1);
当点Q(Q′)在点C下方时,
同理可得:CQ′=7﹣2,
则点Q′(6,2﹣8);
综上所述,Q(0,2,2﹣3).
(
1
/
6
)
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求。
1.下列实数中满足不等式x>3的是( )
A.(﹣2)3 B.π C. D.
2.蝴蝶颜色炫丽,翩翩起舞时非常美丽,深受人们喜爱,如图,蝴蝶图案关于y轴对称1,若点M的坐标为(﹣2,﹣3),则点M1的坐标为( )
A.(2,﹣3) B.(﹣3,2) C.(﹣2,3) D.(2,3)
3.若式子在实数范围内有意义,则x的取值范围为( )
A.x<0 B.x≤0 C.x>0 D.x≥0
4.如图是某几何体的展开图,则此几何体是( )
A.五棱柱 B.五棱锥 C.六棱柱 D.六棱锥
5.将一把折扇展开,可抽象成一个扇形,若该扇形的半径为2,则扇形的圆心角大小为( )
A.30° B.60° C.90° D.120°
6.如图,每只蜻蜓有6条腿,2对翅膀,1对翅膀.现有若干蜻蜓和蝉,共有42条腿,则蜻蜓和蝉的只数分别是( )
A.3,4 B.4,3 C.2,5 D.5,2
7.如图,在△ABC中,AB=5,DE⊥AC,垂足为E,则DE的长为( )
A.1 B.2 C.3 D.5
8.已知关于x的一元二次方程x2﹣2(k﹣1)x+k2+2=0有实数根,则k的取值范围为( )
A. B. C. D.
9.如图,在边长为2的正六边形ABCDEF中,连接BE,点G为EF的中点,当△AGH的周长最小时( )
A. B. C.12 D.13
10.如图,电路上有S1,S2,S3,S4四个断开的开关和一个正常的小灯泡L,将这些开关随机闭合至少两个,能让灯泡发光的概率为( )
A. B. C. D.
11.如图,将全体正偶数排成一个三角数阵,从上向下数有无数多行,第二行有2个数为4,6,…第n行有n个数…….探究其中规律( )
A.36 B.96 C.226 D.426
12.如图,在四边形ABCD中,AB⊥BC,AD∥CF,AF=CF=2AD=2,CD⊥DE,则BF=( )
A. B. C. D.
二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上。
13.因式分解:2x2+8x+8= .
14.中国是茶叶的故乡,产量多年位居世界第一,据统计:2023年我国全年茶叶产量为355万吨 .
15.已知单项式3a2b与﹣2a2bn﹣1是同类项,则n= .
16.如图,直线a∥b,点O在b上,交a于不同两点A,B.若θ=44° °.
17.超市销售某种礼盒,该礼盒的原价为500元.因销量持续攀升,商家在3月份提价20%,于是经过核算决定在3月份售价的基础上,4,5月份按照相同的降价率r连续降价.已知5月份礼盒的售价为486元 ,
18.如图,在矩形ABCD中,点E在AB上运动,将△ADE沿DE翻折,点A落在点F处(靠近点A)时,且,,则cos∠ABF= .
三、解答题:本大题共7个小题,共90分。解答应写出文字说明、证明过程或演算步骤。
19.(1)计算:;
(2)先化简,再求值:,其中.
20.某市射击队将从甲、乙两名运动员中选拔一人参加全省比赛,现对他们进行了6次测试,成绩(单位:环)
甲 7 9 7 9 10 6
乙 5 8 9 10 10 6
(1)根据表格中的数据填空:
甲的平均成绩是 环,乙的平均成绩是 环;甲成绩的中位数是 环,乙成绩的众数是 环.
(2)求甲、乙测试成绩的方差;
(3)你认为推荐谁参加全省比赛更合适,请说明理由.
21.为进一步美化环境,提升生活品质,某部门决定购买甲、乙两种花卉布置公园走廊.预算资金为2700元,其余资金购买乙种花卉.已知乙种花卉每株的价格是甲种花卉每株价格的1.2倍,且购买乙种花卉的数量比甲种花卉多2株.
(1)求甲、乙两种花卉每株的价格;
(2)购买当日正逢花卉促销,甲、乙两种花卉均按原价八折销售.已知该部门需购买甲、乙两种花卉共120株,总费用不超预算
22.如图,在正方形ABCD中,AB=2,点E在线段AO上(与端点不重合),线段EB绕点E逆时针旋转90°到EF的位置,FH⊥AC,垂足为H.
(1)求证:△OBE≌△HEF;
(2)设OE=x,求OE2﹣CF的最小值.
23.如图,在边长为4的菱形ABCD中,对角线AC与BD相交于点E,∠BAD=60°,B(﹣1,0),点C在反比例函数
(1)求点C,D,E的坐标及反比例函数的解析式;
(2)将菱形ABCD向右平移,当点E恰好在反比例函数的图象上时,边BC与函数图象交于点F
24.如图,⊙O为△ABC的外接圆,弦CD⊥AB,直径BF交CD于点G,连接AF,.
(1)证明:四边形ADGF为平行四边形;
(2)求为值;
(3)求sin∠CAD的值.
25.如图,抛物线y=ax2+bx+3(a≠0)与x轴交于点A(﹣3,0)和B(1,0),连接AC和BC,点P在抛物线上运动,BP和CP.
(1)求抛物线的解析式,并写出其顶点坐标;
(2)点P在抛物线上从点A运动到点C的过程中(点P与点A,C不重合),作点P关于x轴的对称点P1,连接AP1,CP1,记△ACP1的面积为S1,记△BCP的面积为S2,若满足S1=3S2,求△ABP的面积;
(3)在(2)的条件下,试探究在y轴上是否存在一点Q,求出点Q的坐标;若不存在
2024年四川省绵阳市中考数学试题
参考答案
一、选择题:本大题共12个小题,每小题3分,共36分.每个小题只有一个选项符合题目要求。
1.B 2.A 3.C 4.C 5.D 6.A 7.B
8.D 9.B 10.D 11.C 12.D
二、填空题:本大题共6个小题,每小题4分,共24分.将答案填写在答题卡相应的横线上。
13.8(x+2)2 14.8.55×106 15.2 16.92 17.10% 18.
三、解答题:本大题共7个小题,共90分。解答应写出文字说明、证明过程或演算步骤。
19.解:(1)
=4++2|8﹣
=3++2(6﹣
=6++2﹣
=0;
(2)
=
=,
当时,原式===.
20.解:(1)甲的平均成绩是(7×2+9×8+10+6)=8(环),
乙的平均成绩是(5+6+9+10×2+7)=8(环),
甲成绩的中位数是=8(环),
乙成绩的众数是10环.
故答案为:6,8,8,10;
(2)=[(6﹣8)2×6+(9﹣8)6×2+(10﹣8)4+(6﹣8)5]=2;
=[(5﹣4)2+(8﹣8)2+(9﹣3)2+2×(10﹣5)2+(6﹣2)2]=;
(3)推荐甲参加全省比赛更合适,理由如下:
因为两人的平均数相同,但甲的方差比乙小,所以推荐甲参加全省比赛更合适.
21.解:(1)设甲种花卉每株的价格为x元,则乙种花卉每株的价格为1.2x元,
由题意得:﹣=2,
解得:x=25,
经检验,x=25是原方程的解,
∴2.2x=1.6×25=30,
答:甲种花卉每株的价格为25元,乙种花卉每株的价格为30元;
(2)设该部门需购买甲种花卉m株,则需购买乙种花卉(120﹣m)株,
由题意得:,
解得:45≤m≤50,
∵m为正整数,
∴m=45,46,48,50,
∴购买这两种花卉有6种方案,
设该部门购买甲、乙两种花卉所需费用为y元,
由题意得:y=25×0.7m+30×0.8(120﹣m)=﹣3m+2880,
∵﹣4<0,
∴y随m的增大而减小,
∴当m=50时,y有最小值=﹣3×50+2880=2680,
答:购买这两种花卉有6种方案,所需费用的最小值为2680元.
22.(1)证明:∵四边形ABCD是正方形,
∴AC⊥BD,
∴∠BOE=90°,
∵FH⊥AC,
∴∠EHF=90°=∠BOE,
∴∠BEO+∠OBE=90°,
由旋转得:BE=EF,∠BEF=90°,
∴∠BEO+∠FEH=90°,
∴∠OBE=∠FEH,
在△OBE和△HEF中,
,
∴△OBE≌△HEF(AAS);
(2)解:∵四边形ABCD是正方形,
∴AB=BC=2,OB=OC=,
∵△OBE≌△HEF,
∴OE=FH=x,EH=OB=,
∴FH=CH=x,
∴CF=FH=x,
∴OE3﹣CF=x2﹣x=(x﹣)2﹣,
∵点E在线段AO上(与端点不重合),
∴0<x<,
∴当x=时,OE8﹣CF的最小值是﹣.
23.解:(1)过点D作DH⊥AB于点H.
∵四边形ABCD是菱形,
∴AB=BC=CD=AD=4,DE=EB,
∵∠BAD=60°,
∴△ABD是等边三角形,
∵DH⊥AB,
∴AH=BH=2,DH=,
∵B(﹣1,7),
∴OB=1,
∴OH=OB+BH=3,
∴D(﹣3,2),C(8,2),
∵DE=EB,
∴E(﹣5,),
∵点C在反比例函数的图象上,
∴k=2,
∴反比例函数的解析式为y=;
(2)对于反比例函数y=,
当y=时,x=2,
∴当点E恰好在反比例函数的图象上时,点E的对应点E′(2,),
∴菱形向右平移了4个单位,
∴B,C的对应点B′(3,C′(7,2),
∴直线B′C′的解析式为y=x﹣3,
由,
解得x=或x=,
∵x>3,
∴点F的坐标为(,),
∴点F到x轴的距离为.
24.(1)证明:∵BF是⊙O的直径,
∴∠BAF=90°,
∴AF⊥AB,
∵CD⊥AB,
∴CD∥AF,
∴DG∥AF,
∴∠AFB=∠BGD,
∵=,
∴∠ADC=∠ABC,
∵=,
∴∠ACB=∠AFB,
∴∠ADC=∠BGD,
∴AD∥GF,
∴四边形ADGF为平行四边形;
(2)解:设BE=x,
∵AB=AC=5,
∴AE=AB﹣BE=5﹣x,
∵AB⊥CD,
∴∠BEC=∠AEC=90°,
∴BC6﹣BE2=AC2﹣AE4=CE2,
∵BC=2,
∴(2)8﹣x2=58﹣(5﹣x)2,
解得x=4,
∴BE=2,AE=3,
∴,
由(1)知,∠ADC=∠BGD,
∵∠AED=∠BEG,
∴△ADE∽△BGE,
∴,
∴;
(3)解:过点D作DH⊥AC于H,
在Rt△BCE中,CE==,
∵=,
∴∠BAD=∠BCD,
∵∠AED=∠CEB,
∴△AED∽△CEB,
∴,
∴,
∴AD=,DE=,
∴CD=CE+DE=4+,
∵S△ACD==AC DH,
∴×3=2DH,
∴DH=,
在Rt△ADH中,sin=,
∴sin∠CAD=.
25.解:(1)由题意得:y=a(x+3)(x﹣1)=a(x8+2x﹣3)=ax5+2ax﹣3a=ax6+bx+3,
则﹣3a=5,则a=﹣1,
则抛物线的表达式为:y=﹣x2﹣2x+3,
该抛物线的对称轴为直线x=﹣1,
当x=﹣8时,y=4,4);
(3)由抛物线的表达式知,点C(8,
设点P(m,﹣m2﹣2m+7),则点P1(m,m2+7m﹣3),
由点A、C的坐标得,则点E(m,
同理由点B、P的坐标得,
连接PP1交AC于点E,设直线PB交y轴于点D,m+6),
则S1=P1E×OA=3×(m+3﹣m3﹣2m+3)=(﹣m2﹣m+7),
同理可得:S2=CD×(xB﹣xP)=(4﹣m﹣3)×(1﹣m)=S1=(﹣m2﹣m+6),
解得:m=(舍去)或﹣,
即点P(﹣,8);
则△ABP的面积=AB×yP=(2+3)×2;
(3)存在,理由:
由(2)知,P(﹣,3);
由点C、P的坐标得﹣;
当点Q在点C的上方时,则∠CPQ=45°,
由点C、P的坐标得,
过点Q作QH⊥PC于点H,
设QH=(2﹣)x,
则PC=3﹣=(2﹣,
解得:x=,
则CH=x=,QH=),
则CQ==3,
则OQ=3+6﹣2=3,
即点Q(0,5+1);
当点Q(Q′)在点C下方时,
同理可得:CQ′=7﹣2,
则点Q′(6,2﹣8);
综上所述,Q(0,2,2﹣3).
(
1
/
6
)
同课章节目录
