13.1.1轴对称 课时巩固练 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 13.1.1轴对称 课时巩固练 2024--2025学年上学期初中数学人教版八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 799.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
13.1.1轴对称 课时巩固练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.中国新能源汽车市场快速增长,成为中国汽车行业的一抹亮色.以下的新能源汽车品牌标志中,不是轴对称图形的是( )
A. B. C. D.
2.下列同类型的每个网格中均有两个三角形,其中一个三角形可以由另一个进行轴对称变换得到的是( )
A. B. C. D.
3.如图,是一个的正方形网格.根据图中标示的各点位置,在下列三角形中,与全等的是( )
A. B. C. D.
4.如图,和关于直线l对称,已知,,,则的长为( )
A. B. C. D.无法确定
5.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题,如图所示,,若,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证为( )
A. B. C. D.
6.如图,把一张对边互相平行的纸条折叠,是折痕,若,则的度数为( )
A. B. C. D.
7.如图,两条平行直线,,从点光源射出的光线射到直线上的点,入射角为,然后反射光线射到直线上的点,当这束光线继续从点反射出去后,反射光线与直线的夹角度数为( )
A. B. C. D.
8.下列说法正确的是( )
A.角是轴对称图形,角平分线是它的对称轴
B.等腰三角形是轴对称图形;底边中线是它的对称轴
C.线段是轴对称图形,中垂线是它的一条对称轴
D.所有的直角三角形都不是轴对称图形
9.如图,,P为内一点,A为上一点,B为上一点,当的周长取最小值时,的度数为( )
A. B. C. D.
10.如图,与关于直线l对称,连接,,,其中分别交,于点D,,下列结论:①;②;③直线l垂直平分;④直线与的交点不一定在直线l上.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
二、填空题
11.在线段、等腰三角形、直角三角形和圆这四个图形中,是轴对称图形的有 个.
12.如图,和关于所在直线成轴对称,,则的度数为 °.
13.如图,△ABD和△ACD关于直线AD对称,若S△ABC=10,则图中阴影部分的面积为 .
14.如图,将长方形纸片沿折叠后,点A,B分别落在,的位置,再沿边将折叠到处,已知,则 .
15.如图,方格纸中的每个小方格的边长为1,△ABC是格点三角形(即顶点恰好是小方格的顶点).若格点△ACP与△ABC全等(不与△ABC重合),则所有满足条件的点P有 个.
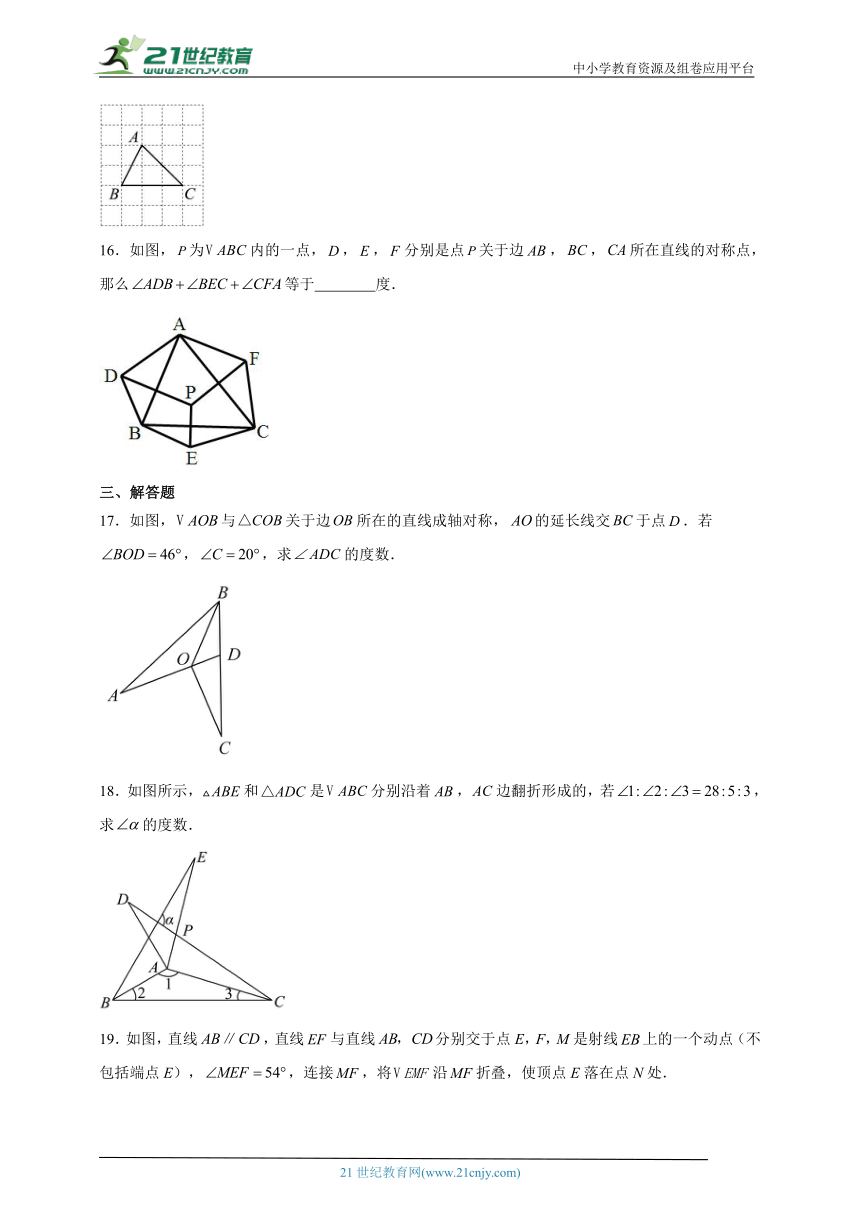
16.如图,为内的一点,,,分别是点关于边,,所在直线的对称点,那么等于 度.
三、解答题
17.如图,与关于边所在的直线成轴对称,的延长线交于点.若,,求的度数.
18.如图所示,和是分别沿着,边翻折形成的,若,求的度数.
19.如图,直线,直线与直线分别交于点E,F,M是射线上的一个动点(不包括端点E),,连接,将沿折叠,使顶点E落在点N处.
(1)求的度数.
(2)当点N恰好落在上时,求的度数.
(3)若,求的度数.
参考答案:
1.C
A、∵是轴对称图形,
∴不符合题意;
B、∵是轴对称图形,
∴不符合题意;
C、∵不是轴对称图形,
∴符合题意;
D、∵是轴对称图形,,
∴不符合题意;
2.B
解:由图形可得,
A选项图形中一个三角形不可以由另一个进行轴对称变换得到,
B选项图形中一个三角形可以由另一个进行轴对称变换得到,
C选项图形中一个三角形不可以由另一个进行轴对称变换得到,
D选项图形中一个三角形不可以由另一个进行轴对称变换得到,
3.C
解:
由图可知:点与点关于对称,
由轴对称的性质可知:
4.B
解:∵和关于直线l对称,
∴,
∴,
5.C
解:,,
,
,
,
6.B
解:∵ ,
∴,
∴,
∴,
7.A
解:如图,
∵从点光源射出的光线射到直线上的点,入射角为,然后反射光线射到直线上的点,
∴,
∵,
∴,
∴当这束光线继续从点反射出去后,反射光线与直线的夹角度数为.
8.C
A、角是轴对称图形,它的角平分线所在直线就是对称轴,故此选项错误;
B、等腰三角形的顶角平分线,底边上的中线和高三线合一,故此选项错误;
C、线段是轴对称图形,它的对称轴是线段的垂直平分线和线段所在的直线,故本选项正确;
D、等腰直角三角形是轴对称图形,故此选项错误.
9.B
解:如图:作P点关于的对称点,然后连接,
∵点与点P关于直线对称,点与点P关于对称,
∴,
∴,
∵,
∴,
∴,
在中,由三角形的内角和定理可知:,
∴,
∴.
10.A
解:和关于直线对称,
∴,故①正确,
和关于直线对称,点D与点关于直线对称的对称点,
∴,故②正确;
和关于直线对称,
线段、、被直线垂直平分,
直线垂直平分,故③正确;
和关于直线对称,
线段、所在直线的交点一定在直线上,故④错误,
∴正确的有①②③,
11.3
解:线段、等腰三角形和圆都能找到一条(或多条) 直线,使图形沿一条直线折叠直线两旁的部分能够互相重合,所以是轴对称图形;
直角三角形(等腰直角三角形除外) 不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
所以是轴对称图形的有3个,
故答案为:3.
12.
解: ,
∴
和关于成轴对称,
,
故答案为:.
13.5
解:∵△ABD和△ACD关于直线AD对称,
∴S△CEF=S△BEF,
∴阴影部分的面积=S△ABC=×10=5,
故答案为:5;
14./18度
解:由折叠性质得:,,,
∵,
∴,
∴,
∵四边形是长方形,
∴,
∴,,
∴,
∴,
∴,
∴,
∴.
故答案为:.
15.3
解:如图,把沿直线对折可得:
把沿直线对折可得:
所以符合条件的点有3个,
故答案为:3
16.360
如图,连接,,,
∵,分别是点关于边,所在直线的对称点,
∴,,
∴,
同理可求,,
∵,
∴,
∴
=
=720°-360
=360°.
故答案为360
17.
与关于边所在的直线成轴对称,
,
,,
,
,
,
.
18.
解:根据题意设,,,
则,
解得,
则,,,
由折叠的性质可知,,
,,
,,
.
19.(1)
(2)
(3)或
(1)解:∵,
∴.
∵,
∴.
(2)如图,点N落在上,
∴.
∵,
∴,
∴.
∵,
∴.
(3)设.
①当点N在平行线之间时(如图).
∵,
∴,
由折叠可知,
∴,
∴,
∴;
②当点N在下方时(如图).
∵,
∴.
由折叠可知,
∴,
解得,
∴.
综上所述,符合题意的的度数为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
13.1.1轴对称 课时巩固练
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.中国新能源汽车市场快速增长,成为中国汽车行业的一抹亮色.以下的新能源汽车品牌标志中,不是轴对称图形的是( )
A. B. C. D.
2.下列同类型的每个网格中均有两个三角形,其中一个三角形可以由另一个进行轴对称变换得到的是( )
A. B. C. D.
3.如图,是一个的正方形网格.根据图中标示的各点位置,在下列三角形中,与全等的是( )
A. B. C. D.
4.如图,和关于直线l对称,已知,,,则的长为( )
A. B. C. D.无法确定
5.数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题,如图所示,,若,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证为( )
A. B. C. D.
6.如图,把一张对边互相平行的纸条折叠,是折痕,若,则的度数为( )
A. B. C. D.
7.如图,两条平行直线,,从点光源射出的光线射到直线上的点,入射角为,然后反射光线射到直线上的点,当这束光线继续从点反射出去后,反射光线与直线的夹角度数为( )
A. B. C. D.
8.下列说法正确的是( )
A.角是轴对称图形,角平分线是它的对称轴
B.等腰三角形是轴对称图形;底边中线是它的对称轴
C.线段是轴对称图形,中垂线是它的一条对称轴
D.所有的直角三角形都不是轴对称图形
9.如图,,P为内一点,A为上一点,B为上一点,当的周长取最小值时,的度数为( )
A. B. C. D.
10.如图,与关于直线l对称,连接,,,其中分别交,于点D,,下列结论:①;②;③直线l垂直平分;④直线与的交点不一定在直线l上.其中正确的是( )
A.①②③ B.②③④ C.①②④ D.①③④
二、填空题
11.在线段、等腰三角形、直角三角形和圆这四个图形中,是轴对称图形的有 个.
12.如图,和关于所在直线成轴对称,,则的度数为 °.
13.如图,△ABD和△ACD关于直线AD对称,若S△ABC=10,则图中阴影部分的面积为 .
14.如图,将长方形纸片沿折叠后,点A,B分别落在,的位置,再沿边将折叠到处,已知,则 .
15.如图,方格纸中的每个小方格的边长为1,△ABC是格点三角形(即顶点恰好是小方格的顶点).若格点△ACP与△ABC全等(不与△ABC重合),则所有满足条件的点P有 个.
16.如图,为内的一点,,,分别是点关于边,,所在直线的对称点,那么等于 度.
三、解答题
17.如图,与关于边所在的直线成轴对称,的延长线交于点.若,,求的度数.
18.如图所示,和是分别沿着,边翻折形成的,若,求的度数.
19.如图,直线,直线与直线分别交于点E,F,M是射线上的一个动点(不包括端点E),,连接,将沿折叠,使顶点E落在点N处.
(1)求的度数.
(2)当点N恰好落在上时,求的度数.
(3)若,求的度数.
参考答案:
1.C
A、∵是轴对称图形,
∴不符合题意;
B、∵是轴对称图形,
∴不符合题意;
C、∵不是轴对称图形,
∴符合题意;
D、∵是轴对称图形,,
∴不符合题意;
2.B
解:由图形可得,
A选项图形中一个三角形不可以由另一个进行轴对称变换得到,
B选项图形中一个三角形可以由另一个进行轴对称变换得到,
C选项图形中一个三角形不可以由另一个进行轴对称变换得到,
D选项图形中一个三角形不可以由另一个进行轴对称变换得到,
3.C
解:
由图可知:点与点关于对称,
由轴对称的性质可知:
4.B
解:∵和关于直线l对称,
∴,
∴,
5.C
解:,,
,
,
,
6.B
解:∵ ,
∴,
∴,
∴,
7.A
解:如图,
∵从点光源射出的光线射到直线上的点,入射角为,然后反射光线射到直线上的点,
∴,
∵,
∴,
∴当这束光线继续从点反射出去后,反射光线与直线的夹角度数为.
8.C
A、角是轴对称图形,它的角平分线所在直线就是对称轴,故此选项错误;
B、等腰三角形的顶角平分线,底边上的中线和高三线合一,故此选项错误;
C、线段是轴对称图形,它的对称轴是线段的垂直平分线和线段所在的直线,故本选项正确;
D、等腰直角三角形是轴对称图形,故此选项错误.
9.B
解:如图:作P点关于的对称点,然后连接,
∵点与点P关于直线对称,点与点P关于对称,
∴,
∴,
∵,
∴,
∴,
在中,由三角形的内角和定理可知:,
∴,
∴.
10.A
解:和关于直线对称,
∴,故①正确,
和关于直线对称,点D与点关于直线对称的对称点,
∴,故②正确;
和关于直线对称,
线段、、被直线垂直平分,
直线垂直平分,故③正确;
和关于直线对称,
线段、所在直线的交点一定在直线上,故④错误,
∴正确的有①②③,
11.3
解:线段、等腰三角形和圆都能找到一条(或多条) 直线,使图形沿一条直线折叠直线两旁的部分能够互相重合,所以是轴对称图形;
直角三角形(等腰直角三角形除外) 不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
所以是轴对称图形的有3个,
故答案为:3.
12.
解: ,
∴
和关于成轴对称,
,
故答案为:.
13.5
解:∵△ABD和△ACD关于直线AD对称,
∴S△CEF=S△BEF,
∴阴影部分的面积=S△ABC=×10=5,
故答案为:5;
14./18度
解:由折叠性质得:,,,
∵,
∴,
∴,
∵四边形是长方形,
∴,
∴,,
∴,
∴,
∴,
∴,
∴.
故答案为:.
15.3
解:如图,把沿直线对折可得:
把沿直线对折可得:
所以符合条件的点有3个,
故答案为:3
16.360
如图,连接,,,
∵,分别是点关于边,所在直线的对称点,
∴,,
∴,
同理可求,,
∵,
∴,
∴
=
=720°-360
=360°.
故答案为360
17.
与关于边所在的直线成轴对称,
,
,,
,
,
,
.
18.
解:根据题意设,,,
则,
解得,
则,,,
由折叠的性质可知,,
,,
,,
.
19.(1)
(2)
(3)或
(1)解:∵,
∴.
∵,
∴.
(2)如图,点N落在上,
∴.
∵,
∴,
∴.
∵,
∴.
(3)设.
①当点N在平行线之间时(如图).
∵,
∴,
由折叠可知,
∴,
∴,
∴;
②当点N在下方时(如图).
∵,
∴.
由折叠可知,
∴,
解得,
∴.
综上所述,符合题意的的度数为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
