深圳市中考备考百师助学培优课程——第3讲:《将军饮马与最值问题》课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第3讲:《将军饮马与最值问题》课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 486.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 09:46:28 | ||
图片预览


文档简介
(共18张PPT)
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
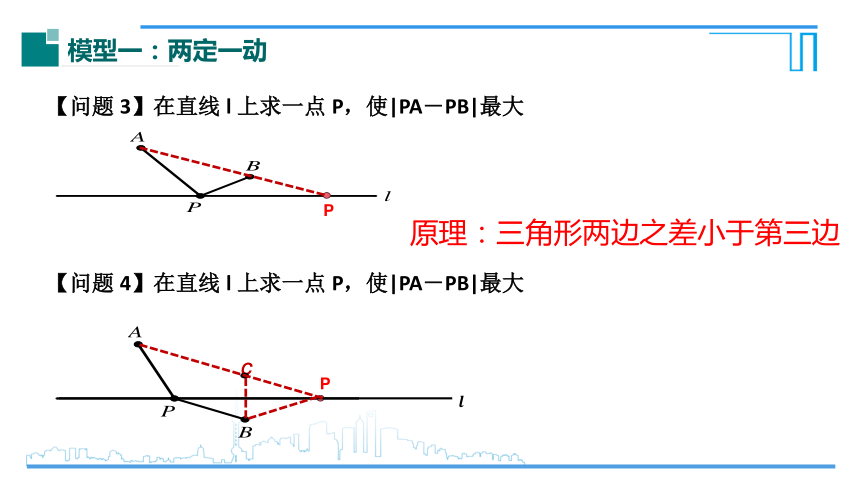
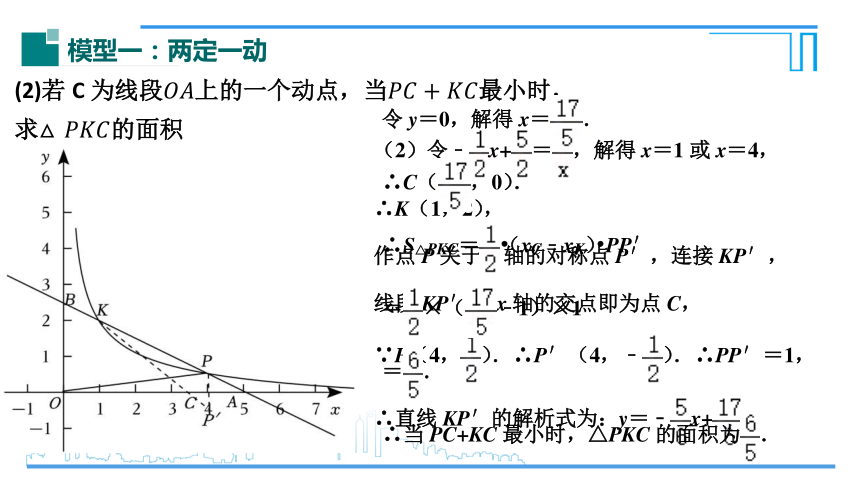
模型一:两定一动
深圳市红桂中学 陈伟钊
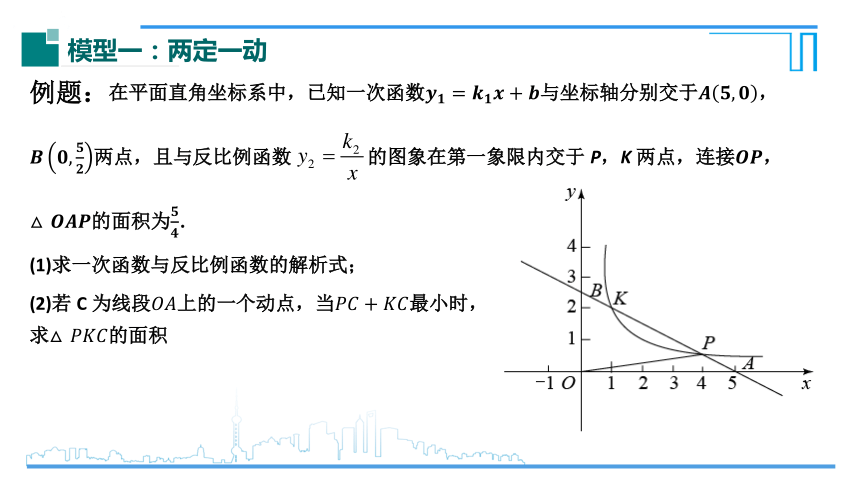
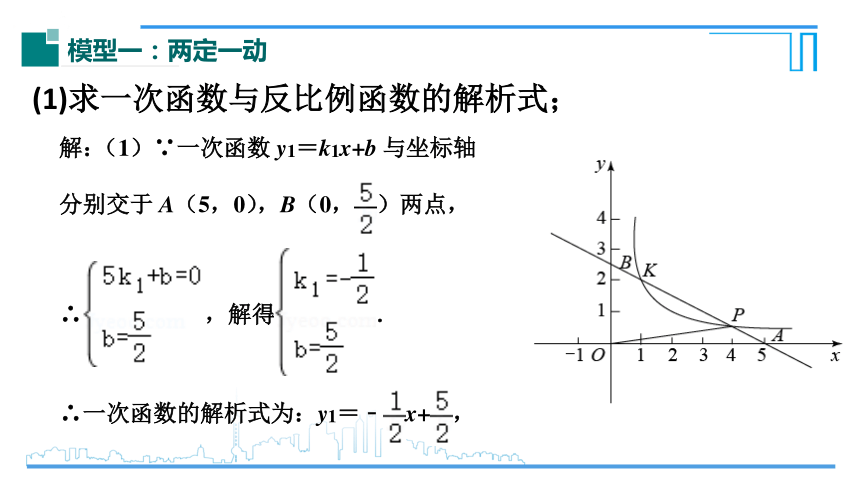
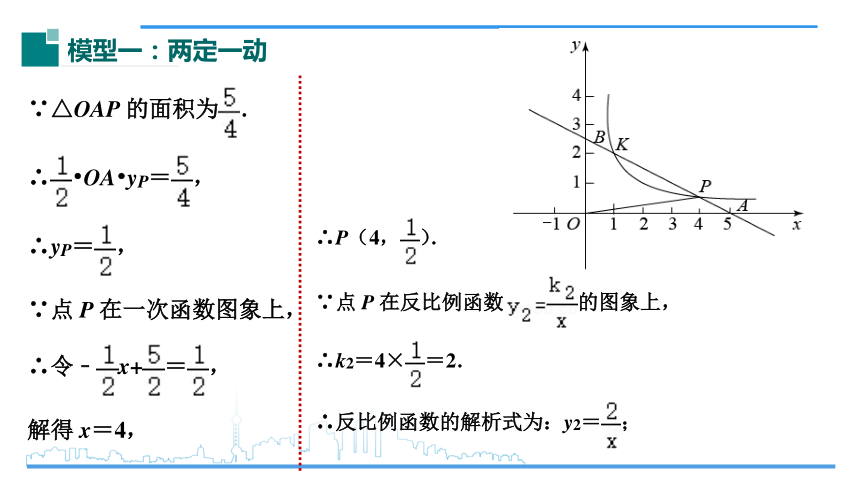
模型一:两定一动
原理:两点之间,线段最短
P
C
A
B
l
P
P
C
P
原理:三角形两边之差小于第三边
模型一:两定一动
模型一:两定一动
模型一:两定一动
模型一:两定一动
模型一:两定一动
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
模型二:一定两动
深圳市红桂中学 陈伟钊
模型一:一定两动
C
原理:垂段最短
B
A
模型一:一定两动
N
M
模型一:一定两动
模型一:一定两动
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
模型三:两定两动
深圳市红桂中学 陈伟钊
模型三:两定两动
原理:两点之间,线段最短
,N,M, 共线时取最小,则 AN+MN+BM
= N+MN+M
≤
B
N
M
A
N
M
模型三:两定两动
原理:两点之间,线段最短,
连接,与两直线交点即为M,N, 则 PM+MN+QN的最小值线段的长,周长最小值为+PQ
M
P
Q
N
N
M
N
M
A
B
模型三:两定两动
原理:通过平移构造平行四边A
AM= =
则 AM+MN+BN= +MN+BN
当M三点共线时AM+MN+BN最小
即+MN+BN= B+MN
此时四边形ABMN周长最小
例题1:如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为 。
模型三:两定两动
模型三:两定两动
例题2:如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 .
(﹣,0)
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
模型一:两定一动
深圳市红桂中学 陈伟钊
模型一:两定一动
原理:两点之间,线段最短
P
C
A
B
l
P
P
C
P
原理:三角形两边之差小于第三边
模型一:两定一动
模型一:两定一动
模型一:两定一动
模型一:两定一动
模型一:两定一动
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
模型二:一定两动
深圳市红桂中学 陈伟钊
模型一:一定两动
C
原理:垂段最短
B
A
模型一:一定两动
N
M
模型一:一定两动
模型一:一定两动
罗湖区中考备考“百师助学”培优课程之《将军饮马与最值问题》
模型三:两定两动
深圳市红桂中学 陈伟钊
模型三:两定两动
原理:两点之间,线段最短
,N,M, 共线时取最小,则 AN+MN+BM
= N+MN+M
≤
B
N
M
A
N
M
模型三:两定两动
原理:两点之间,线段最短,
连接,与两直线交点即为M,N, 则 PM+MN+QN的最小值线段的长,周长最小值为+PQ
M
P
Q
N
N
M
N
M
A
B
模型三:两定两动
原理:通过平移构造平行四边A
AM= =
则 AM+MN+BN= +MN+BN
当M三点共线时AM+MN+BN最小
即+MN+BN= B+MN
此时四边形ABMN周长最小
例题1:如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为 。
模型三:两定两动
模型三:两定两动
例题2:如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 .
(﹣,0)
同课章节目录
