深圳市中考备考百师助学培优课程——第2讲:中点常见问题及辅助线做法 课件
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第2讲:中点常见问题及辅助线做法 课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 43.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 09:46:28 | ||
图片预览







文档简介
(共26张PPT)
第2讲 中点常见问题及辅助线作法
罗湖区中考备考“百师助学”课程
深圳市罗湖区翠园实验学校 黄缨
中线等分三角形面积
模型一:三角形中线
中线等分三角形面积
AD是△ABC的中线,
则 S△ABD=S△ACD= S△ABC.
典型例题
1.如图,在 ABC中,D,E分别是BC,AD的中点,点F在BE上,且EF=2BF. 若S BCF=2cm2,则S ABC 为( ).
A.4cm2 B.8cm2 C.12cm2 D.16cm2
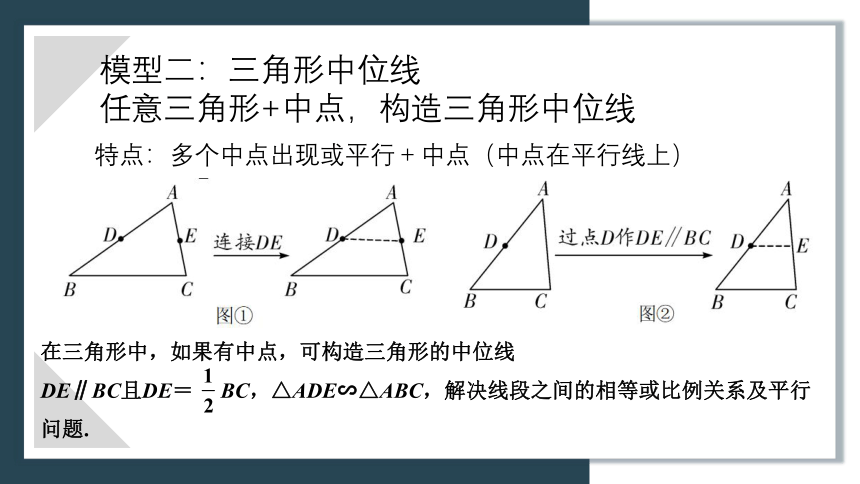
模型二:三角形中位线
任意三角形+中点,构造三角形中位线
在三角形中,如果有中点,可构造三角形的中位线
DE∥BC且DE= BC,△ADE∽△ABC,解决线段之间的相等或比例关系及平行问题.
特点:多个中点出现或平行+中点(中点在平行线上)
典型例题
2.(2023 泰安中考)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B.64 C.22 D.2
典型例题
(2023 泰安中考)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
选A. 解:取OB中点N,连接MN,AN.
在Rt△OCD中,OD=4,∠D=30°,
∴OC=4,
∵M、N分别是BC、OB的中点,
∴MN= OC=2,
在△ABN中,AB=4,BN=3,
∴AN=5,
在△AMN中,AM>AN﹣MN;
当M运动到AN上时,AM=AN﹣MN,
∴AM≥AN﹣MN=5﹣2=3,
∴线段AM的最小值是3.
典型例题
3.(2023年四川巴中)如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为( ).
A.2cm2 B.4cm2 C.6cm2 D.8cm2
典型例题
3.(2023年四川巴中)如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为( ).
A.2cm2 B.4cm2 C.6cm2 D.8cm2
模型三:等腰三角形“三线合一”
特点:在等腰三角形中,底边有中点.
等腰三角形中有底边上的中点时,常作边的中线
由等腰三角形“三线合一”得到:∠BAD=∠CAD,AD⊥BC,常常用于解决线段相等及平行问题、角度之间的相等问题.
典型例题
4. 如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,则MN的长为 .
典型例题
5.(2023四川自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
典型例题
5.(2023四川自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
模型四:直角三角形“斜边上的中线”
特点:在直角三角形中,有斜边上的中点.
在直角三角形中,当遇见斜边中点时,常会作斜边上的中线.
在Rt△ABC中,∠C=90°,点D为AB的中点,作斜边上的中线CD,则有CD=AD=BD=
作用:①证明线段相等或求线段长;
②构造角相等进行等量代换
6.(2023深圳适应性考试)如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°, 对角线AC与BD相交于点E,若BE=3DE,则BD=__________.
典型例题
7.(2023四川凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是 _________.
典型例题
6.(2023四川凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是 _________.
模型五:倍长中线
特点:三角形中出现中线或类中线(与中点有关的线段).
当遇见中线或者中点时,可以尝试用倍长中线法构造全等三角形,证线段间的数量关系.
7.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是__________.
典型例题
7.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是__________.
典型例题
模型六:圆中弦、弧的中点
特点:圆中出现中点.
圆中遇到弦、弧的中点,常联想“垂径定理”“圆周角定理”“弦、弧、圆心角、圆周角之间的关系”.
8.(2023四川宜宾)如图,已知点A,B,C在⊙O上,C为AB 的中点.若∠BAC=35°,则∠AOB等于( )
A.140° B.120° C.110° D.70°
模型七:平面直角坐标系中的中点坐标
特点:在平面直角坐标系中出现中点.
如图,在平面直角坐标系中,已知A(x1,y1),B(x2,y2),点M为线段AB的中点,则点M的坐标为 .
9.(2023 济宁)如图,直线y=﹣x+4交x轴于点B,交y轴于点C,抛物线y=﹣x2+3x+4经过B,C两点,交x轴负半轴于点A,P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.
若m< ,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m的值;若不存在,请说明理由.
9(2023 济宁)如图,直线y=﹣x+4交x轴于点B,交y轴于点C,抛物线y=﹣x2+3x+4经过B,C两点,交x轴负半轴于点A,P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.
若m< ,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m的值;若不存在,请说明理由.
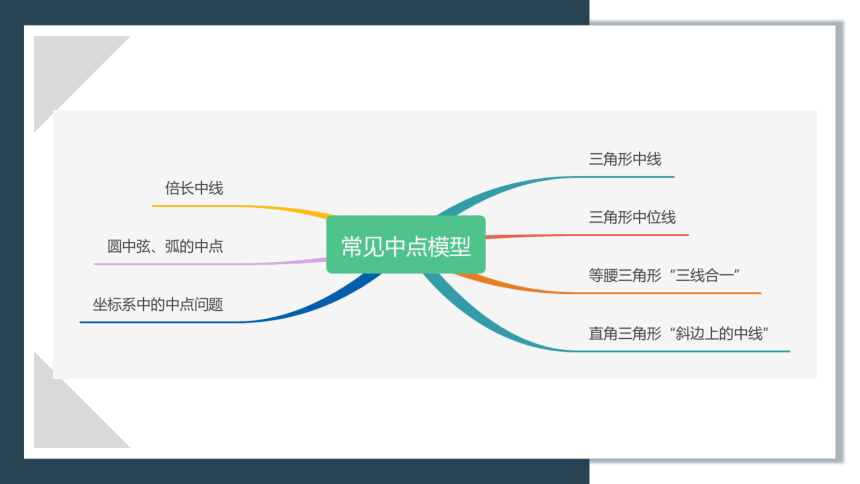
你能用思维导图的方式总结中点问题的常见类型及其辅助线的主要内容吗?
第2讲 中点常见问题及辅助线作法
罗湖区中考备考“百师助学”课程
深圳市罗湖区翠园实验学校 黄缨
中线等分三角形面积
模型一:三角形中线
中线等分三角形面积
AD是△ABC的中线,
则 S△ABD=S△ACD= S△ABC.
典型例题
1.如图,在 ABC中,D,E分别是BC,AD的中点,点F在BE上,且EF=2BF. 若S BCF=2cm2,则S ABC 为( ).
A.4cm2 B.8cm2 C.12cm2 D.16cm2
模型二:三角形中位线
任意三角形+中点,构造三角形中位线
在三角形中,如果有中点,可构造三角形的中位线
DE∥BC且DE= BC,△ADE∽△ABC,解决线段之间的相等或比例关系及平行问题.
特点:多个中点出现或平行+中点(中点在平行线上)
典型例题
2.(2023 泰安中考)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
A.3 B.64 C.22 D.2
典型例题
(2023 泰安中考)如图,在平面直角坐标系中,Rt△AOB的一条直角边OB在x轴上,点A的坐标为(﹣6,4);Rt△COD中,∠COD=90°,OD=4,∠D=30°,连接BC,点M是BC中点,连接AM.将Rt△COD以点O为旋转中心按顺时针方向旋转,在旋转过程中,线段AM的最小值是( )
选A. 解:取OB中点N,连接MN,AN.
在Rt△OCD中,OD=4,∠D=30°,
∴OC=4,
∵M、N分别是BC、OB的中点,
∴MN= OC=2,
在△ABN中,AB=4,BN=3,
∴AN=5,
在△AMN中,AM>AN﹣MN;
当M运动到AN上时,AM=AN﹣MN,
∴AM≥AN﹣MN=5﹣2=3,
∴线段AM的最小值是3.
典型例题
3.(2023年四川巴中)如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为( ).
A.2cm2 B.4cm2 C.6cm2 D.8cm2
典型例题
3.(2023年四川巴中)如图,在Rt△ABC中,AB=6cm,BC=8cm,D、E分别为AC、BC中点,连接AE、BD相交于点F,点G在CD上,且DG:GC=1:2,则四边形DFEG的面积为( ).
A.2cm2 B.4cm2 C.6cm2 D.8cm2
模型三:等腰三角形“三线合一”
特点:在等腰三角形中,底边有中点.
等腰三角形中有底边上的中点时,常作边的中线
由等腰三角形“三线合一”得到:∠BAD=∠CAD,AD⊥BC,常常用于解决线段相等及平行问题、角度之间的相等问题.
典型例题
4. 如图,在△ABC中,AB=AC=5,BC=6,M为BC的中点,MN⊥AC于点N,则MN的长为 .
典型例题
5.(2023四川自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
典型例题
5.(2023四川自贡)如图1,一大一小两个等腰直角三角形叠放在一起,M,N分别是斜边DE,AB的中点,DE=2,AB=4.
将△CDE绕顶点C逆时针旋转120°(如图2),求MN的长.
模型四:直角三角形“斜边上的中线”
特点:在直角三角形中,有斜边上的中点.
在直角三角形中,当遇见斜边中点时,常会作斜边上的中线.
在Rt△ABC中,∠C=90°,点D为AB的中点,作斜边上的中线CD,则有CD=AD=BD=
作用:①证明线段相等或求线段长;
②构造角相等进行等量代换
6.(2023深圳适应性考试)如图,在四边形ABCD中,AB=BC=6,∠ABC=60°,∠ADC=90°, 对角线AC与BD相交于点E,若BE=3DE,则BD=__________.
典型例题
7.(2023四川凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是 _________.
典型例题
6.(2023四川凉山州)如图,边长为2的等边△ABC的两个顶点A、B分别在两条射线OM、ON上滑动,若OM⊥ON,则OC的最大值是 _________.
模型五:倍长中线
特点:三角形中出现中线或类中线(与中点有关的线段).
当遇见中线或者中点时,可以尝试用倍长中线法构造全等三角形,证线段间的数量关系.
7.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是__________.
典型例题
7.如图,在△ABC中,∠ACB=120°,BC=4,D为AB的中点,DC⊥BC,则△ABC的面积是__________.
典型例题
模型六:圆中弦、弧的中点
特点:圆中出现中点.
圆中遇到弦、弧的中点,常联想“垂径定理”“圆周角定理”“弦、弧、圆心角、圆周角之间的关系”.
8.(2023四川宜宾)如图,已知点A,B,C在⊙O上,C为AB 的中点.若∠BAC=35°,则∠AOB等于( )
A.140° B.120° C.110° D.70°
模型七:平面直角坐标系中的中点坐标
特点:在平面直角坐标系中出现中点.
如图,在平面直角坐标系中,已知A(x1,y1),B(x2,y2),点M为线段AB的中点,则点M的坐标为 .
9.(2023 济宁)如图,直线y=﹣x+4交x轴于点B,交y轴于点C,抛物线y=﹣x2+3x+4经过B,C两点,交x轴负半轴于点A,P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.
若m< ,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m的值;若不存在,请说明理由.
9(2023 济宁)如图,直线y=﹣x+4交x轴于点B,交y轴于点C,抛物线y=﹣x2+3x+4经过B,C两点,交x轴负半轴于点A,P为抛物线上一动点,点P的横坐标为m,过点P作x轴的平行线交抛物线于另一点M,作x轴的垂线PN,垂足为N,直线MN交y轴于点D.
若m< ,设直线MN交直线BC于点E,是否存在这样的m值,使MN=2ME?若存在,求出此时m的值;若不存在,请说明理由.
你能用思维导图的方式总结中点问题的常见类型及其辅助线的主要内容吗?
同课章节目录
