深圳市中考备考百师助学培优课程——第3讲:《将军饮马与最值问题》 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第3讲:《将军饮马与最值问题》 教学设计 |  | |
| 格式 | docx | ||
| 文件大小 | 232.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 09:46:28 | ||
图片预览


文档简介
罗湖区中考备考“百师助学”课程之《将军饮马与最值问题》
深圳市红桂中学 陈伟钊
一、内容分析
最值问题在现实生活中经常遇到,初中阶段主要以“两点之间,线段最短”以及“连接直线外一点与直线上各点的所有线段中,垂线段最短”、三角形三边关系为基础知识,有时还要借助轴对称、平移、旋转等变换进行研究.
本专题以“将军饮马模型”为载体开展对最值问题的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”以及“连接直线外一点与直线上各点的所有线段中,垂线段最短”、三角形三边关系问题.
二、学情分析
作为初中生,在解决最值问题这方面的数学经验尚显不足,特别是面对具有实际背景的最值问题,更会感到陌生,无从下手.
三、教学任务分析
1.教学目标
能利用轴对称、平移解决最值问题,体会图形的变化在解决最值问题中的作用,感悟领会转化的数学思想,培养学生探究问题的兴趣和合作交流的意识,感受数学的实用性,体验自己探究出问题的成就感.
2.教学重点
利用轴对称、平移等变换将线段和、差最值问题转化为“两点之间,线段最短”“垂线段最短”、三角形三边关系问题.
四、教学过程
步骤 教学主要内容 教师活动 学生活动 设计意图
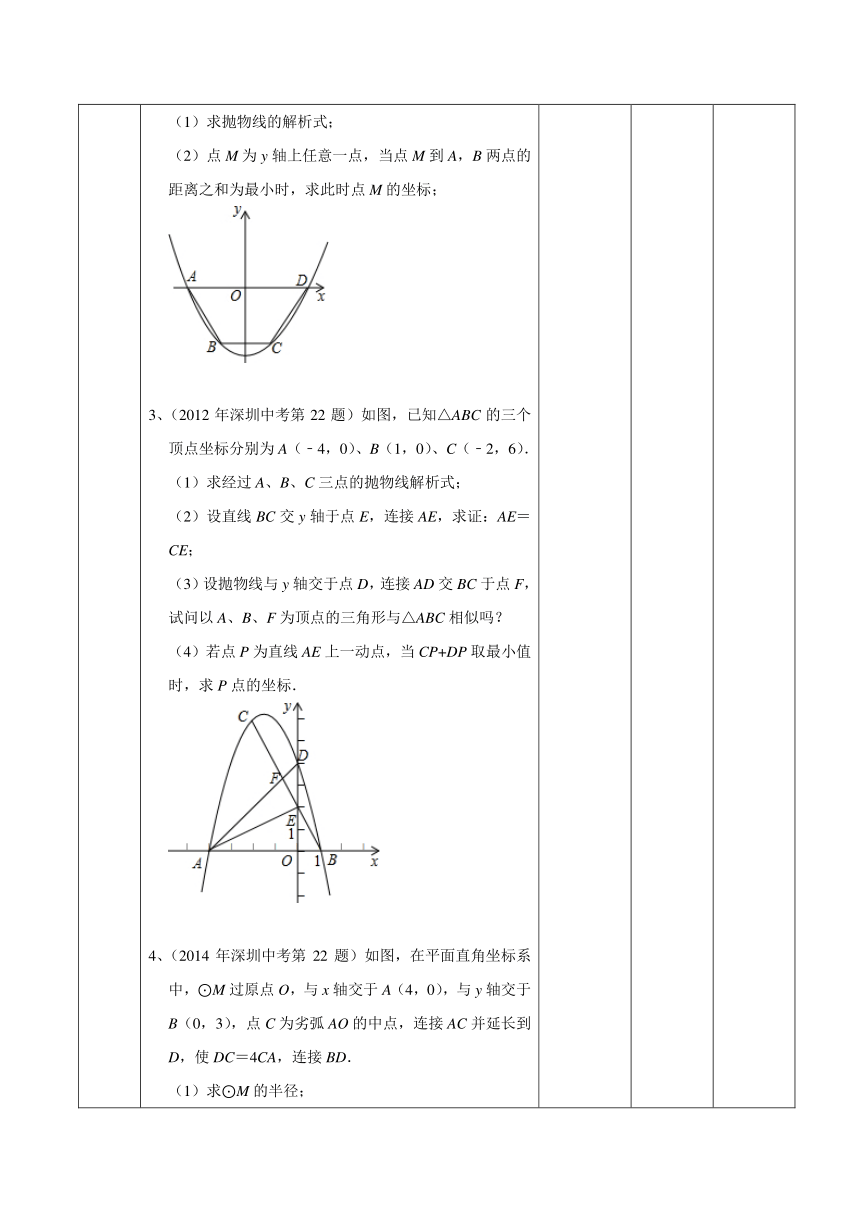
模型一:两定一动 【问题1】在直线l上求一点P,使PA+PB最小 【问题2】在直线l上求一点P,使PA+PB最小 【问题3】在直线l上求一点P,使|PA-PB|最大 【问题4】在直线l上求一点P,使|PA-PB|最大 例题:在平面直角坐标系中,已知一次函数与坐标轴分别交于,两点,且与反比例函数的图象在第一象限内交于P,K两点,连接, 的面积为. (1)求一次函数与反比例函数的解析式; (2)若C为线段上的一个动点,当最小时,求的面积. 跟进练习: 1、(2008年深圳中考第14题)要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是 . 2、(2010年深圳中考第22题)如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3). (1)求抛物线的解析式; (2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标; 3、(2012年深圳中考第22题)如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6). (1)求经过A、B、C三点的抛物线解析式; (2)设直线BC交y轴于点E,连接AE,求证:AE=CE; (3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗? (4)若点P为直线AE上一动点,当CP+DP取最小值时,求P点的坐标. 4、(2014年深圳中考第22题)如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD. (1)求⊙M的半径; (2)证明:BD为⊙M的切线; (3)在直线MC上找一点P,使|DP﹣AP|最大. 教师提问:求线段和最小值,线段差最大值的原理 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理。 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
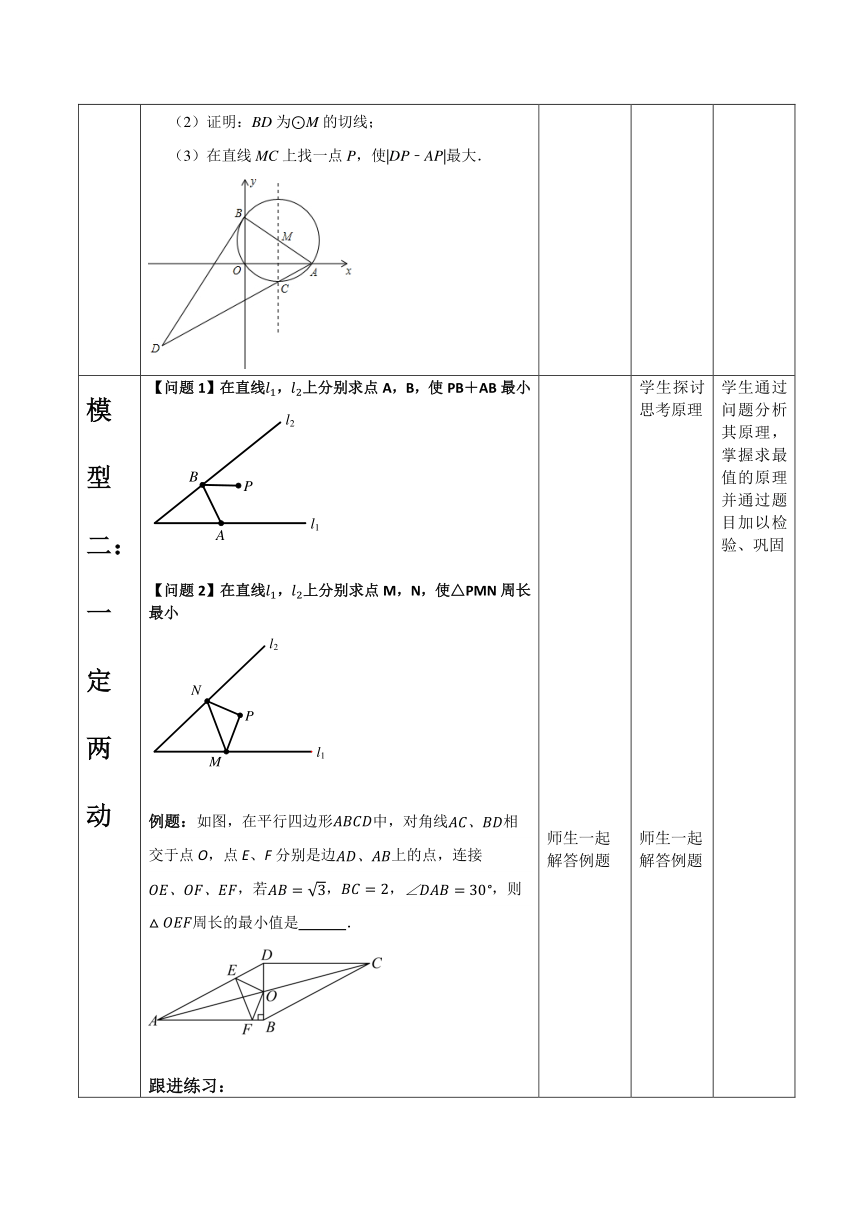
模型二:一定两动 【问题1】在直线,上分别求点A,B,使PB+AB最小 【问题2】在直线,上分别求点M,N,使△PMN周长最小 例题:如图,在平行四边形中,对角线相交于点O,点E、F分别是边上的点,连接,若,,,则周长的最小值是 . 跟进练习: 1、如图,点P是∠AOB内任意一点,∠AOB=30°,OP=6,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________. 2、(2023下·湛江·二模)如图,在中,,,,,平分交于点,点、分别是、边上的动点,则的最小值为 . 3、如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN. (1)求抛物线的解析式及点D的坐标; (2)当△CMN是直角三角形时,求点M的坐标; (3)试求出AM+AN的最小值. 4、(2023·西安·二模)如图,在四边形中,,,,,、分别是边、上的动点,连接,,,则周长的最小值为 . 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
模型三:两定两动 【问题1】A,B分别为,上的定点,M,N分别为,上的动点,求最小值 【问题2】P,Q为定点,在直线,上分别求点M,N,使四边形PQMN周长最小 【问题3】在直线l上求两点M,N(M在左)且MN=a,求四边形ABNM周长的最小值 例题1:如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为 。 例题2:如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 . 跟踪练习: 如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为 . 2、(2011年深圳中考第23题)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0). (1)求抛物线的解析式; (2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G,H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由; 3、(2019年深圳中考第22题)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC. (1)求抛物线的解析式及其对称轴; (2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值. 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
板书设计 解题思路: 确定动点运动轨迹 求出定点关于运动轨迹的对称点 由两点确定函数表达式 (或由两点距离公式求出线段和最小值) 联立运动轨迹的函数表达式求出交点坐标 教师引导,学生总结解题思路 学生总结解题思路
深圳市红桂中学 陈伟钊
一、内容分析
最值问题在现实生活中经常遇到,初中阶段主要以“两点之间,线段最短”以及“连接直线外一点与直线上各点的所有线段中,垂线段最短”、三角形三边关系为基础知识,有时还要借助轴对称、平移、旋转等变换进行研究.
本专题以“将军饮马模型”为载体开展对最值问题的课题研究,让学生经历将实际问题抽象为数学的线段和最小问题,再利用轴对称将线段和最小问题转化为“两点之间,线段最短”以及“连接直线外一点与直线上各点的所有线段中,垂线段最短”、三角形三边关系问题.
二、学情分析
作为初中生,在解决最值问题这方面的数学经验尚显不足,特别是面对具有实际背景的最值问题,更会感到陌生,无从下手.
三、教学任务分析
1.教学目标
能利用轴对称、平移解决最值问题,体会图形的变化在解决最值问题中的作用,感悟领会转化的数学思想,培养学生探究问题的兴趣和合作交流的意识,感受数学的实用性,体验自己探究出问题的成就感.
2.教学重点
利用轴对称、平移等变换将线段和、差最值问题转化为“两点之间,线段最短”“垂线段最短”、三角形三边关系问题.
四、教学过程
步骤 教学主要内容 教师活动 学生活动 设计意图
模型一:两定一动 【问题1】在直线l上求一点P,使PA+PB最小 【问题2】在直线l上求一点P,使PA+PB最小 【问题3】在直线l上求一点P,使|PA-PB|最大 【问题4】在直线l上求一点P,使|PA-PB|最大 例题:在平面直角坐标系中,已知一次函数与坐标轴分别交于,两点,且与反比例函数的图象在第一象限内交于P,K两点,连接, 的面积为. (1)求一次函数与反比例函数的解析式; (2)若C为线段上的一个动点,当最小时,求的面积. 跟进练习: 1、(2008年深圳中考第14题)要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是 . 2、(2010年深圳中考第22题)如图所示,抛物线y=ax2+c(a>0)经过梯形ABCD的四个顶点,梯形的底AD在x轴上,其中A(﹣2,0),B(﹣1,﹣3). (1)求抛物线的解析式; (2)点M为y轴上任意一点,当点M到A,B两点的距离之和为最小时,求此时点M的坐标; 3、(2012年深圳中考第22题)如图,已知△ABC的三个顶点坐标分别为A(﹣4,0)、B(1,0)、C(﹣2,6). (1)求经过A、B、C三点的抛物线解析式; (2)设直线BC交y轴于点E,连接AE,求证:AE=CE; (3)设抛物线与y轴交于点D,连接AD交BC于点F,试问以A、B、F为顶点的三角形与△ABC相似吗? (4)若点P为直线AE上一动点,当CP+DP取最小值时,求P点的坐标. 4、(2014年深圳中考第22题)如图,在平面直角坐标系中,⊙M过原点O,与x轴交于A(4,0),与y轴交于B(0,3),点C为劣弧AO的中点,连接AC并延长到D,使DC=4CA,连接BD. (1)求⊙M的半径; (2)证明:BD为⊙M的切线; (3)在直线MC上找一点P,使|DP﹣AP|最大. 教师提问:求线段和最小值,线段差最大值的原理 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理。 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
模型二:一定两动 【问题1】在直线,上分别求点A,B,使PB+AB最小 【问题2】在直线,上分别求点M,N,使△PMN周长最小 例题:如图,在平行四边形中,对角线相交于点O,点E、F分别是边上的点,连接,若,,,则周长的最小值是 . 跟进练习: 1、如图,点P是∠AOB内任意一点,∠AOB=30°,OP=6,点M和点N分别是射线OA和射线OB上的动点,则△PMN周长的最小值为___________. 2、(2023下·湛江·二模)如图,在中,,,,,平分交于点,点、分别是、边上的动点,则的最小值为 . 3、如图,抛物线y=ax2﹣5ax+c与坐标轴分别交于点A,C,E三点,其中A(﹣3,0),C(0,4),点B在x轴上,AC=BC,过点B作BD⊥x轴交抛物线于点D,点M,N分别是线段CO,BC上的动点,且CM=BN,连接MN,AM,AN. (1)求抛物线的解析式及点D的坐标; (2)当△CMN是直角三角形时,求点M的坐标; (3)试求出AM+AN的最小值. 4、(2023·西安·二模)如图,在四边形中,,,,,、分别是边、上的动点,连接,,,则周长的最小值为 . 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
模型三:两定两动 【问题1】A,B分别为,上的定点,M,N分别为,上的动点,求最小值 【问题2】P,Q为定点,在直线,上分别求点M,N,使四边形PQMN周长最小 【问题3】在直线l上求两点M,N(M在左)且MN=a,求四边形ABNM周长的最小值 例题1:如图所示,E为边长是2的正方形ABCD的中点,M为BC上一点,N为CD上一点,连EM、MN、NA,则四边形AEMN周长的最小值为 。 例题2:如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,顶点A,C分别在x轴,y轴上,B,D两点坐标分别为B(﹣4,6),D(0,4),线段EF在边OA上移动,保持EF=3,当四边形BDEF的周长最小时,点E的坐标为 . 跟踪练习: 如图,在平面直角坐标系中,已知,在x轴上取两点C,D(点C在点D左侧),且始终保持,线段在x轴上平移,当的值最小时,点C的坐标为 . 2、(2011年深圳中考第23题)如图1,抛物线y=ax2+bx+c(a≠0)的顶点为C(1,4),交x轴于A、B两点,交y轴于点D,其中点B的坐标为(3,0). (1)求抛物线的解析式; (2)如图2,过点A的直线与抛物线交于点E,交y轴于点F,其中点E的横坐标为2,若直线PQ为抛物线的对称轴,点G为直线PQ上的一动点,则x轴上是否存在一点H,使D、G,H、F四点所围成的四边形周长最小?若存在,求出这个最小值及点G、H的坐标;若不存在,请说明理由; 3、(2019年深圳中考第22题)如图抛物线y=ax2+bx+c经过点A(﹣1,0),点C(0,3),且OB=OC. (1)求抛物线的解析式及其对称轴; (2)点D、E是直线x=1上的两个动点,且DE=1,点D在点E的上方,求四边形ACDE的周长的最小值. 师生一起解答例题 教师巡视学生解题情况,答疑解惑 学生探讨思考原理 师生一起解答例题 学生先独立思考后,再相互探讨 学生通过问题分析其原理,掌握求最值的原理并通过题目加以检验、巩固
板书设计 解题思路: 确定动点运动轨迹 求出定点关于运动轨迹的对称点 由两点确定函数表达式 (或由两点距离公式求出线段和最小值) 联立运动轨迹的函数表达式求出交点坐标 教师引导,学生总结解题思路 学生总结解题思路
同课章节目录
