深圳市中考备考百师助学培优课程——第1讲:中考作图题 教学设计
文档属性
| 名称 | 深圳市中考备考百师助学培优课程——第1讲:中考作图题 教学设计 |

|
|
| 格式 | docx | ||
| 文件大小 | 232.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 09:46:28 | ||
图片预览



文档简介
“尺规作图”教学设计
设计者:深圳市罗湖区桂园中学 郭培香
一、教学目标:
1.知识与技能:(1)再认识什么是尺规作图,经历五个基本作图的复习与巩固,能在解答题中按要求进行尺规作图(不要求写出具体做法,但需要保留作图痕迹);(2)能在题目中识别出具体是哪种类型的尺规作图,并利用所做的线的性质来解决几何问题。
2.过程与方法:经历五个基本作图的复习与巩固,感受尺规作图的几何意义,规范学生的作图语言,积累一些尺规作图的方法与经验,感受数学的严谨性以及数学结论的确定性。
3.情感、态度与价值观:通过复习尺规作图,进一步加强学生的作图能力,使学生养成良好的动手操作、实践探索、合作交流的学习习惯。
二、教学重点:
掌握五个基本尺规作图的作法
三、教学难点:
能利用尺规作图解决实际问题
四、教学过程:
知识技能梳理
1.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
2. 五种基本作图:
1)作一条线段等于已知线段;
2)作已知角的平分线;
3)作已知线段的垂直平分线;
4)作一个角等于已知角;
5)过一点作已知直线的垂线【点在线上、点在线外】。
模块一:五种尺规作图复习
1.作一条线段等于已知线段
已知:如图所示线段a.
求作:线段AB,使AB = a.
作法:
(1)作射线AP;
(2)在射线AP上截取AB=a.则线段AB就是所求作的图形。
作线段的垂直平分线(中垂线)或中点
已知:如图,线段MN.
求作:线段MN的垂直平分线.
作法:
(1)分别以M、N为圆心,大于的长为半径画弧,两弧相交于P,Q;
(2)连接PQ交MN于O.
则直线PQ就是线段MN的垂直平分线。
3.作已知角的平分线
已知:如图,∠AOB.
求作:射线OP, 使∠AOP=∠BOP(即OP平分∠AOB).
作法:
(1)以O为圆心,任意长度为半径画弧,分别交OA,OB于M,N;
(2)分别以M、N为圆心,大于的线段长为半径画弧,两弧交∠AOB内于P;
作射线OP。
则射线OP就是∠AOB的角平分线。
4.作一个角等于已知角
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
1)作射线O′A′;
2)以O为圆心,任意长度为半径画弧,交OA于M,交OB于N;
3)以O′为圆心,以OM的长为半径画弧,交O′A′于M′;
4)以M′为圆心,以MN的长为半径画弧,交前弧于N′;
5)连接O′N′并延长到B′。
则∠A′O′B′就是所求作的角。
5.过一点作已知直线的垂线
已知点在直线上
已知:直线l、及直线l上一点C
求作:直线l的垂线,使得垂线经过点C
作法:
(1)以点C为圆心,任一线段的长为半径画弧,交直线l于点A、B;
(2)以点A 、B为圆心,以大于CB长为半径在直线一侧画弧,两弧交于点D;
(3)经过点C、D作直线CD.
直线CD即为所求.
已知点在直线外
已知:直线l、及直线l外一点C
求作:直线l的垂线,使得直线l经过点C
作法:
(1)以点C为圆心,以适当长为半径画弧,交直线l于点A、B;
(2)分别以点A、 B为圆心,以CB长为半径在直线另一侧画弧,两弧于点D.
(3)经过点C、D作直线CD.
直线CD即为所求.
模块二:分题型练习
作相等线段出现等腰三角形
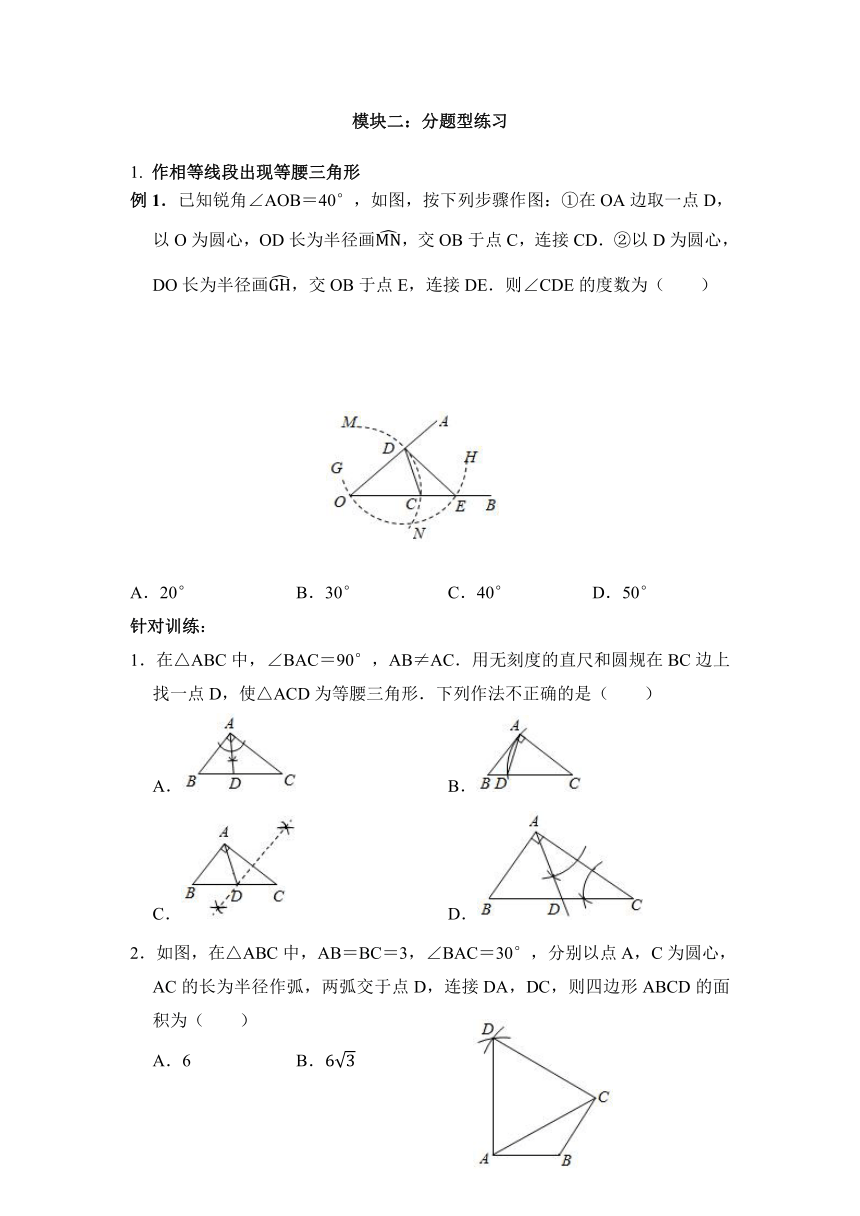
例1.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
针对训练:
1.在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
A. B.
C. D.
2.如图,在△ABC中,AB=BC=3,∠BAC=30°,分别以点A,C为圆心,AC的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为( )
A.6 B.
C.9 D.
3.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
角平分线及性质应用
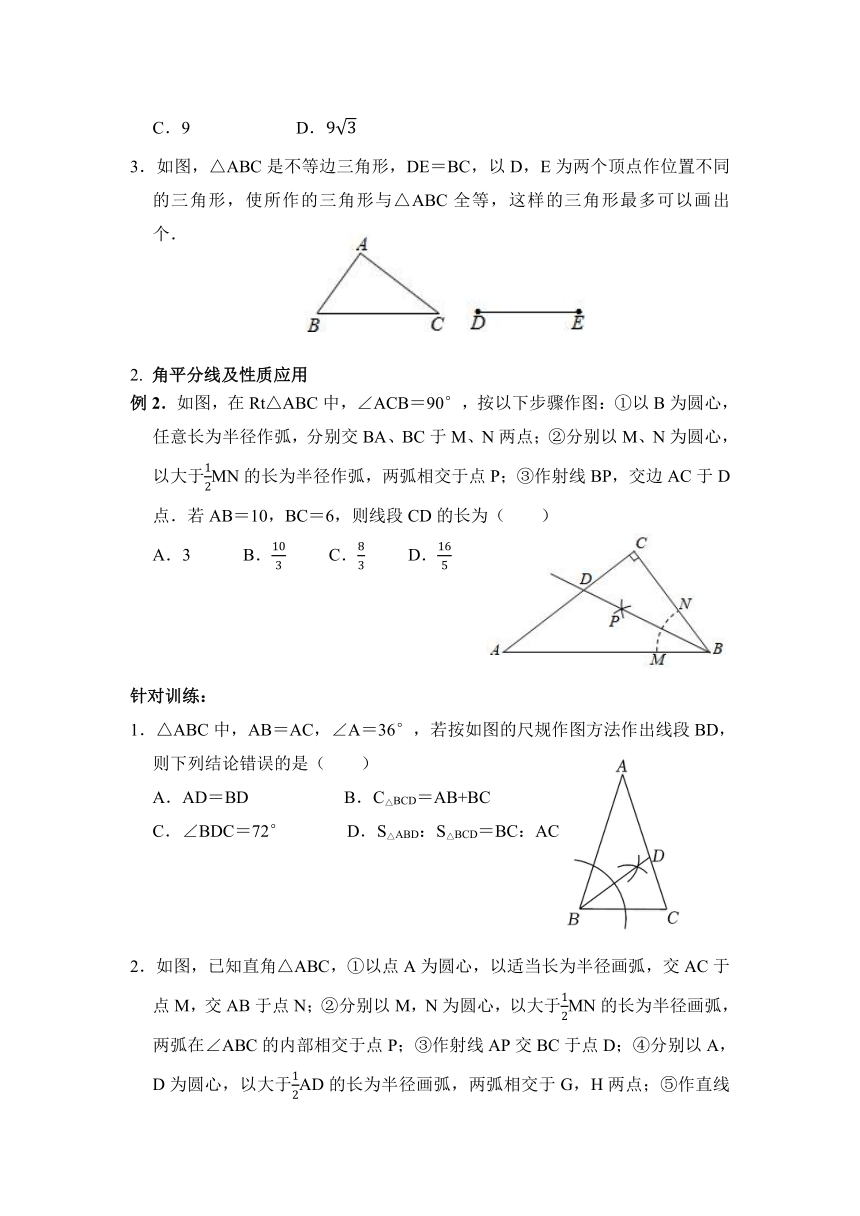
例2.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
针对训练:
1.△ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )
A.AD=BD B.C△BCD=AB+BC
C.∠BDC=72° D.S△ABD:S△BCD=BC:AC
2.如图,已知直角△ABC,①以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠ABC的内部相交于点P;③作射线AP交BC于点D;④分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点;⑤作直线GH,分别交AC,AB于点E,F.
依据以上作图,若AF=3,CE=1,则CD的长是( )
A. B.2 C. D.3
中垂线及性质应用
例3.如图,在 ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是( )
A.2 B.3 C.4 D.5
针对训练:
下列三幅图都是“作已知三角形的高”的尺规作图过程,其中作图正确的是( )
A.(1)(2)(3)B.(1)(2) C.(1)(3) D.(2)(3)
2.如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有 个.
模块三:综合应用
角平分线+中垂线综合
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
针对训练:
如图所示,在Rt△ACB中,∠ACB=90°,根据尺规作图的痕迹,可以判断以下结论错误的是( )
ED=CD B.AC=AE
∠EDB=∠CAB D.∠DAC=∠B
中垂线与将军饮马模型
例2. ∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3),M,N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN周长的最小值是 .
针对训练:
要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是 .
角平分线加三角形综合
例3.某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在等腰△ABC中,其中AB=AC,如图Ⅰ,进行了如下操作:
第一步,以点A为圆心,任意长为半径画弧,分别交BA的延长线和AC于点E,F,如图Ⅱ;
第二步,分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点D,作射线AD;
第三步,以D为圆心,DA的长为半径画弧,交射线AE于点G;
(1)填空;写出∠CAD与∠GAD的大小关系为 ;
(2)①请判断AD与BC的位置关系,并说明理由.
②当AB=AC=6,BC=2时,连接DG,请直接写出 ;
(3)如图Ⅲ,根据以上条件,点P为AB的中点,点M为射线AD上的一个动点,连接PM,PC,当∠CPM=∠B时,求AM的长.
针对训练:
下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.
小明:如图1,(1)分别在射线OA,OB上截取OC=OD,OE=OF(点C,E不重合);(2)分别作线段CE,DF的垂直平分线l1,l2,交点为P,垂足分别为点G,H;(3)作射线OP,射线OP即为∠AOB的平分线. 简述理由如下: 由作图知,∠PGO=∠PHO=90°,OG=OH,OP=OP,所以Rt△PGO≌Rt△PHO,则∠POG=∠POH,即射线OP是∠AOB的平分线. 小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2,(1)分别在射线OA,OB上截取OC=OD,OE=OF(点C,E不重合);(2)连接DE,CF,交点为P;(3)作射线OP.射线OP即为∠AOB的平分线. ……
任务:
(1)小明得出Rt△PGO≌Rt△PHO的依据是 (填序号).
①SSS②SAS③AAS④ASA⑤HL
(2)小军作图得到的射线OP是∠AOB的平分线吗?请判断并说明理由.
(3)如图3,已知∠AOB=60°,点E,F分别在射线OA,OB上,且OE=OF1.点C,D分别为射线OA,OB上的动点,且OC=OD,连接DE,CF,交点为P,当∠CPE=30°时,直接写出线段OC的长.
圆与尺规作图综合
例4. 已知直线l及直线l外一点P.如图,
(1)在直线l上取一点O,以点O为圆心,OP长为半径画半圆,交直线l于A,B两点;
(2)连接PA,以点B为圆心,AP长为半径画弧,交半圆于点Q;
(3)作直线PQ,连接BP.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.AP=BQ B.PQ∥AB
C.∠ABP=∠PBQ D.∠APQ+∠ABQ=180°
针对训练:
如图,在单位长度为1的网格中,点O,A,B均在格点上,OA=3,AB=2,
以O为圆心,OA为半径画圆,请按下列步骤完成作图,并回答问题:
①过点A作切线AC,且AC=4(点C在A的上方);
②连接OC,交⊙O于点D;
③连接BD,与AC交于点E.
(1)求证:DB为⊙O的切线;
(2)求AE的长度.
五、课堂小结
本节课我们重点复习了五个基本尺规作图,并运用这五个基本作图解决了与中考相关的实际问题。
六、作业布置
设计者:深圳市罗湖区桂园中学 郭培香
一、教学目标:
1.知识与技能:(1)再认识什么是尺规作图,经历五个基本作图的复习与巩固,能在解答题中按要求进行尺规作图(不要求写出具体做法,但需要保留作图痕迹);(2)能在题目中识别出具体是哪种类型的尺规作图,并利用所做的线的性质来解决几何问题。
2.过程与方法:经历五个基本作图的复习与巩固,感受尺规作图的几何意义,规范学生的作图语言,积累一些尺规作图的方法与经验,感受数学的严谨性以及数学结论的确定性。
3.情感、态度与价值观:通过复习尺规作图,进一步加强学生的作图能力,使学生养成良好的动手操作、实践探索、合作交流的学习习惯。
二、教学重点:
掌握五个基本尺规作图的作法
三、教学难点:
能利用尺规作图解决实际问题
四、教学过程:
知识技能梳理
1.尺规作图的定义:尺规作图是指用没有刻度的直尺和圆规作图。
2. 五种基本作图:
1)作一条线段等于已知线段;
2)作已知角的平分线;
3)作已知线段的垂直平分线;
4)作一个角等于已知角;
5)过一点作已知直线的垂线【点在线上、点在线外】。
模块一:五种尺规作图复习
1.作一条线段等于已知线段
已知:如图所示线段a.
求作:线段AB,使AB = a.
作法:
(1)作射线AP;
(2)在射线AP上截取AB=a.则线段AB就是所求作的图形。
作线段的垂直平分线(中垂线)或中点
已知:如图,线段MN.
求作:线段MN的垂直平分线.
作法:
(1)分别以M、N为圆心,大于的长为半径画弧,两弧相交于P,Q;
(2)连接PQ交MN于O.
则直线PQ就是线段MN的垂直平分线。
3.作已知角的平分线
已知:如图,∠AOB.
求作:射线OP, 使∠AOP=∠BOP(即OP平分∠AOB).
作法:
(1)以O为圆心,任意长度为半径画弧,分别交OA,OB于M,N;
(2)分别以M、N为圆心,大于的线段长为半径画弧,两弧交∠AOB内于P;
作射线OP。
则射线OP就是∠AOB的角平分线。
4.作一个角等于已知角
已知:∠AOB.
求作:∠A′O′B′,使∠A′O′B′=∠AOB.
作法:
1)作射线O′A′;
2)以O为圆心,任意长度为半径画弧,交OA于M,交OB于N;
3)以O′为圆心,以OM的长为半径画弧,交O′A′于M′;
4)以M′为圆心,以MN的长为半径画弧,交前弧于N′;
5)连接O′N′并延长到B′。
则∠A′O′B′就是所求作的角。
5.过一点作已知直线的垂线
已知点在直线上
已知:直线l、及直线l上一点C
求作:直线l的垂线,使得垂线经过点C
作法:
(1)以点C为圆心,任一线段的长为半径画弧,交直线l于点A、B;
(2)以点A 、B为圆心,以大于CB长为半径在直线一侧画弧,两弧交于点D;
(3)经过点C、D作直线CD.
直线CD即为所求.
已知点在直线外
已知:直线l、及直线l外一点C
求作:直线l的垂线,使得直线l经过点C
作法:
(1)以点C为圆心,以适当长为半径画弧,交直线l于点A、B;
(2)分别以点A、 B为圆心,以CB长为半径在直线另一侧画弧,两弧于点D.
(3)经过点C、D作直线CD.
直线CD即为所求.
模块二:分题型练习
作相等线段出现等腰三角形
例1.已知锐角∠AOB=40°,如图,按下列步骤作图:①在OA边取一点D,以O为圆心,OD长为半径画,交OB于点C,连接CD.②以D为圆心,DO长为半径画,交OB于点E,连接DE.则∠CDE的度数为( )
A.20° B.30° C.40° D.50°
针对训练:
1.在△ABC中,∠BAC=90°,AB≠AC.用无刻度的直尺和圆规在BC边上找一点D,使△ACD为等腰三角形.下列作法不正确的是( )
A. B.
C. D.
2.如图,在△ABC中,AB=BC=3,∠BAC=30°,分别以点A,C为圆心,AC的长为半径作弧,两弧交于点D,连接DA,DC,则四边形ABCD的面积为( )
A.6 B.
C.9 D.
3.如图,△ABC是不等边三角形,DE=BC,以D,E为两个顶点作位置不同的三角形,使所作的三角形与△ABC全等,这样的三角形最多可以画出 个.
角平分线及性质应用
例2.如图,在Rt△ABC中,∠ACB=90°,按以下步骤作图:①以B为圆心,任意长为半径作弧,分别交BA、BC于M、N两点;②分别以M、N为圆心,以大于MN的长为半径作弧,两弧相交于点P;③作射线BP,交边AC于D点.若AB=10,BC=6,则线段CD的长为( )
A.3 B. C. D.
针对训练:
1.△ABC中,AB=AC,∠A=36°,若按如图的尺规作图方法作出线段BD,则下列结论错误的是( )
A.AD=BD B.C△BCD=AB+BC
C.∠BDC=72° D.S△ABD:S△BCD=BC:AC
2.如图,已知直角△ABC,①以点A为圆心,以适当长为半径画弧,交AC于点M,交AB于点N;②分别以M,N为圆心,以大于MN的长为半径画弧,两弧在∠ABC的内部相交于点P;③作射线AP交BC于点D;④分别以A,D为圆心,以大于AD的长为半径画弧,两弧相交于G,H两点;⑤作直线GH,分别交AC,AB于点E,F.
依据以上作图,若AF=3,CE=1,则CD的长是( )
A. B.2 C. D.3
中垂线及性质应用
例3.如图,在 ABCD中,AD=4,对角线BD=8,分别以点A、B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,则GA的长是( )
A.2 B.3 C.4 D.5
针对训练:
下列三幅图都是“作已知三角形的高”的尺规作图过程,其中作图正确的是( )
A.(1)(2)(3)B.(1)(2) C.(1)(3) D.(2)(3)
2.如图,已知每个小方格的边长为1,A,B两点都在小方格的顶点上,请在图中找一个顶点C,使△ABC为等腰三角形,则这样的顶点C有 个.
模块三:综合应用
角平分线+中垂线综合
两个城镇A、B与两条公路ME,MF位置如图所示,其中ME是东西方向公路.现电信部门需在C处修建一座信号发射塔,要求发射塔到两个城镇A、B的距离必须相等,到两条公路ME,MF的距离也必须相等,且在∠FME的内部,请在图中,用尺规作图找出符合条件的点C.(不写已知、求作、作法,只保留作图痕迹)
针对训练:
如图所示,在Rt△ACB中,∠ACB=90°,根据尺规作图的痕迹,可以判断以下结论错误的是( )
ED=CD B.AC=AE
∠EDB=∠CAB D.∠DAC=∠B
中垂线与将军饮马模型
例2. ∠AOB在平面直角坐标系中的位置如图所示,且∠AOB=60°,在∠AOB内有一点P(4,3),M,N分别是OA,OB边上的动点,连接PM,PN,MN,则△PMN周长的最小值是 .
针对训练:
要在街道旁修建一个奶站,向居民区A、B提供牛奶,奶站应建在什么地方,才能使从A、B到它的距离之和最短?小聪根据实际情况,以街道旁为x轴,建立了如图所示的平面直角坐标系,测得A点的坐标为(0,3),B点的坐标为(6,5),则从A、B两点到奶站距离之和的最小值是 .
角平分线加三角形综合
例3.某数学兴趣小组在学习了尺规作图、等腰三角形和相似三角形的有关知识后,在等腰△ABC中,其中AB=AC,如图Ⅰ,进行了如下操作:
第一步,以点A为圆心,任意长为半径画弧,分别交BA的延长线和AC于点E,F,如图Ⅱ;
第二步,分别以点E,F为圆心,大于EF的长为半径画弧,两弧相交于点D,作射线AD;
第三步,以D为圆心,DA的长为半径画弧,交射线AE于点G;
(1)填空;写出∠CAD与∠GAD的大小关系为 ;
(2)①请判断AD与BC的位置关系,并说明理由.
②当AB=AC=6,BC=2时,连接DG,请直接写出 ;
(3)如图Ⅲ,根据以上条件,点P为AB的中点,点M为射线AD上的一个动点,连接PM,PC,当∠CPM=∠B时,求AM的长.
针对训练:
下面是某数学兴趣小组探究用不同方法作一个角的平分线的讨论片段,请仔细阅读,并完成相应的任务.
小明:如图1,(1)分别在射线OA,OB上截取OC=OD,OE=OF(点C,E不重合);(2)分别作线段CE,DF的垂直平分线l1,l2,交点为P,垂足分别为点G,H;(3)作射线OP,射线OP即为∠AOB的平分线. 简述理由如下: 由作图知,∠PGO=∠PHO=90°,OG=OH,OP=OP,所以Rt△PGO≌Rt△PHO,则∠POG=∠POH,即射线OP是∠AOB的平分线. 小军:我认为小明的作图方法很有创意,但是太麻烦了,可以改进如下,如图2,(1)分别在射线OA,OB上截取OC=OD,OE=OF(点C,E不重合);(2)连接DE,CF,交点为P;(3)作射线OP.射线OP即为∠AOB的平分线. ……
任务:
(1)小明得出Rt△PGO≌Rt△PHO的依据是 (填序号).
①SSS②SAS③AAS④ASA⑤HL
(2)小军作图得到的射线OP是∠AOB的平分线吗?请判断并说明理由.
(3)如图3,已知∠AOB=60°,点E,F分别在射线OA,OB上,且OE=OF1.点C,D分别为射线OA,OB上的动点,且OC=OD,连接DE,CF,交点为P,当∠CPE=30°时,直接写出线段OC的长.
圆与尺规作图综合
例4. 已知直线l及直线l外一点P.如图,
(1)在直线l上取一点O,以点O为圆心,OP长为半径画半圆,交直线l于A,B两点;
(2)连接PA,以点B为圆心,AP长为半径画弧,交半圆于点Q;
(3)作直线PQ,连接BP.
根据以上作图过程及所作图形,下列结论中错误的是( )
A.AP=BQ B.PQ∥AB
C.∠ABP=∠PBQ D.∠APQ+∠ABQ=180°
针对训练:
如图,在单位长度为1的网格中,点O,A,B均在格点上,OA=3,AB=2,
以O为圆心,OA为半径画圆,请按下列步骤完成作图,并回答问题:
①过点A作切线AC,且AC=4(点C在A的上方);
②连接OC,交⊙O于点D;
③连接BD,与AC交于点E.
(1)求证:DB为⊙O的切线;
(2)求AE的长度.
五、课堂小结
本节课我们重点复习了五个基本尺规作图,并运用这五个基本作图解决了与中考相关的实际问题。
六、作业布置
同课章节目录
