湖北省黄冈市普通高中2024-2025学年高二上学期期中阶段性联考数学试题(无答案)
文档属性
| 名称 | 湖北省黄冈市普通高中2024-2025学年高二上学期期中阶段性联考数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 482.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 12:45:06 | ||
图片预览

文档简介
湖北省黄冈市普通高中2024-2025学年高二上学期期中阶段性联考数学试题
本试卷共4页,19题。全卷满分150分。考试用时120分钟
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将答题卡上交。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在空间直角坐标系中,点关于平面的对称点为
A. B. C. D.
2.若直线与直线平行,则的值为
A. B.2 C.-2 D.-5
3.近几年7月,武汉持续高温,市气象局将发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温37摄氏度以上的概率是.某人用计算机生成了10组随机数,结果如下:
726 127 821 763 314 245 521 986 402 862
若用0,1,2,3,4表示高温橙色预警,用5,6,7,8,9表示非高温橙色预警,依据该模拟实验,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是
A. B. C. D.
4.某饮料生产企业推出了一种有一定中奖机会的新饮料.甲、乙、丙三名同学都购买了这种饮料,设事件为“甲、乙、丙三名同学都中奖”,则与互为对立事件的是
A.甲、乙、丙恰有两人中奖 B.甲、乙、丙都不中奖
C.甲、乙、丙至少有一人不中奖 D.甲、乙、丙至多有一人不中奖
5.已知点,若,则直线AB的倾斜角的取值范围为
A. B. C. D.
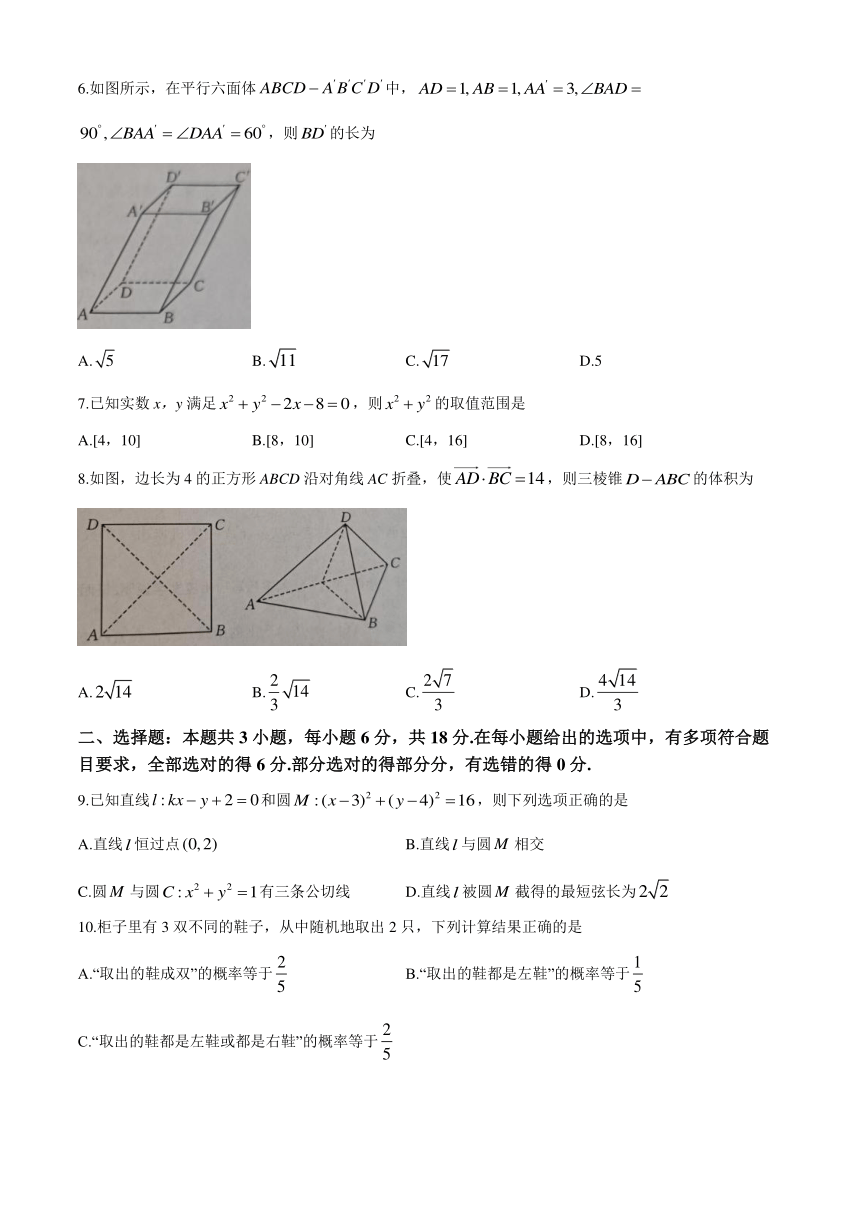
6.如图所示,在平行六面体中,,则的长为
A. B. C. D.5
7.已知实数x,y满足,则的取值范围是
A.[4,10] B.[8,10] C.[4,16] D.[8,16]
8.如图,边长为4的正方形ABCD沿对角线AC折叠,使,则三棱锥的体积为
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分.部分选对的得部分分,有选错的得0分.
9.已知直线和圆,则下列选项正确的是
A.直线恒过点 B.直线与圆相交
C.圆与圆有三条公切线 D.直线被圆截得的最短弦长为
10.柜子里有3双不同的鞋子,从中随机地取出2只,下列计算结果正确的是
A.“取出的鞋成双”的概率等于 B.“取出的鞋都是左鞋”的概率等于
C.“取出的鞋都是左鞋或都是右鞋”的概率等于
D.“取出的鞋一只是左鞋,一只是右鞋,但不成双”的概率等于
11.如图,在棱长为2的正方体中,点为线段BD的中点,且点满足,则下列说法正确的是
A.若,则平面 B.若,则平面
C.若,则到平面的距离为
D.若时,直线DP与平面所成角为,则
三、填空题:本题共3小题,每小题5分,共15分.
12.经过两点的直线的方向向量为,则的值为______.
13.已知空间向量,若共面,则mn的最小值为______.
14.由这2024个正整数构成集合,先从集合中随机取一个数,取出后把放回集合,然后再从集合中随机取出一个数,则的概率为______.
四、解答题:本题共5小题,共77分.解答应写出相应文字说明、证明过程或演算步骤.
15.(本题满分13分)
已知的顶点,边AB上的中线CM所在直线方程为,边AC上的高BH所在直线方程为.
(1)求顶点的坐标;
(2)求直线BC的方程.
16.(本题满分15分)
如图,在四棱锥中,平面为PD的中点.
(1)若,证明:;
(2)若,求平面ACE和平面ECD的夹角的余弦值.
17.(本题满分15分)
某中学根据学生的兴趣爱好,分别创建了“绘画”、“书法”、“诗词”三个兴趣小组,据统计新生通过考核选拔进入这三个兴趣小组成功与否相互独立.2024年某新生入学,假设他通过考核选拔进入该校的“绘画”、“书法”、“诗词”三个兴趣小组的概率依次为,已知三个兴趣小组他都能进入的概率为,至少进入一个兴趣小组的概率为,且.
(1)求与的值;
(2)该校根据兴趣小组活动安排情况,对进入“绘画”兴趣小组的同学增加校本选修学分1分,对进入“书法”兴趣小组的同学增加校本选修学分2分,对进入“诗词”兴趣小组的同学增加校本选修学分3分.求该同学在兴趣小组方面获得校本选修学分分数不低于4分的概率.
18.(本题满分17分)
如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,分别为DC,BC的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
(1)求证:平面;
(2)求点到平面的距离;
(3)在线段上是否存在点,使得直线与平面所成的角为,若存在,求出线段BM的长;若不存在,请说明理由.
19.(本题满分17分)
已知动点M与两个定点的距离的比为,记动点的轨迹为曲线.
(1)求曲线的方程,并说明其形状;
(2)已知,过直线上的动点分别作曲线的两条切线PQ,为切点),连接PD交QR于点,
(ⅰ)证明:直线QR过定点,并求该定点坐标;
(ⅱ)是否存在点P,使的面积最大?若存在,求出点的坐标;若不存在,请说明理由.
本试卷共4页,19题。全卷满分150分。考试用时120分钟
注意事项:
1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。写在试卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内。写在试卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将答题卡上交。
一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.在空间直角坐标系中,点关于平面的对称点为
A. B. C. D.
2.若直线与直线平行,则的值为
A. B.2 C.-2 D.-5
3.近几年7月,武汉持续高温,市气象局将发布高温橙色预警信号(高温橙色预警标准为24小时内最高气温将升至37摄氏度以上),在今后的3天中,每一天最高气温37摄氏度以上的概率是.某人用计算机生成了10组随机数,结果如下:
726 127 821 763 314 245 521 986 402 862
若用0,1,2,3,4表示高温橙色预警,用5,6,7,8,9表示非高温橙色预警,依据该模拟实验,则今后的3天中恰有2天发布高温橙色预警信号的概率估计是
A. B. C. D.
4.某饮料生产企业推出了一种有一定中奖机会的新饮料.甲、乙、丙三名同学都购买了这种饮料,设事件为“甲、乙、丙三名同学都中奖”,则与互为对立事件的是
A.甲、乙、丙恰有两人中奖 B.甲、乙、丙都不中奖
C.甲、乙、丙至少有一人不中奖 D.甲、乙、丙至多有一人不中奖
5.已知点,若,则直线AB的倾斜角的取值范围为
A. B. C. D.
6.如图所示,在平行六面体中,,则的长为
A. B. C. D.5
7.已知实数x,y满足,则的取值范围是
A.[4,10] B.[8,10] C.[4,16] D.[8,16]
8.如图,边长为4的正方形ABCD沿对角线AC折叠,使,则三棱锥的体积为
A. B. C. D.
二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求,全部选对的得6分.部分选对的得部分分,有选错的得0分.
9.已知直线和圆,则下列选项正确的是
A.直线恒过点 B.直线与圆相交
C.圆与圆有三条公切线 D.直线被圆截得的最短弦长为
10.柜子里有3双不同的鞋子,从中随机地取出2只,下列计算结果正确的是
A.“取出的鞋成双”的概率等于 B.“取出的鞋都是左鞋”的概率等于
C.“取出的鞋都是左鞋或都是右鞋”的概率等于
D.“取出的鞋一只是左鞋,一只是右鞋,但不成双”的概率等于
11.如图,在棱长为2的正方体中,点为线段BD的中点,且点满足,则下列说法正确的是
A.若,则平面 B.若,则平面
C.若,则到平面的距离为
D.若时,直线DP与平面所成角为,则
三、填空题:本题共3小题,每小题5分,共15分.
12.经过两点的直线的方向向量为,则的值为______.
13.已知空间向量,若共面,则mn的最小值为______.
14.由这2024个正整数构成集合,先从集合中随机取一个数,取出后把放回集合,然后再从集合中随机取出一个数,则的概率为______.
四、解答题:本题共5小题,共77分.解答应写出相应文字说明、证明过程或演算步骤.
15.(本题满分13分)
已知的顶点,边AB上的中线CM所在直线方程为,边AC上的高BH所在直线方程为.
(1)求顶点的坐标;
(2)求直线BC的方程.
16.(本题满分15分)
如图,在四棱锥中,平面为PD的中点.
(1)若,证明:;
(2)若,求平面ACE和平面ECD的夹角的余弦值.
17.(本题满分15分)
某中学根据学生的兴趣爱好,分别创建了“绘画”、“书法”、“诗词”三个兴趣小组,据统计新生通过考核选拔进入这三个兴趣小组成功与否相互独立.2024年某新生入学,假设他通过考核选拔进入该校的“绘画”、“书法”、“诗词”三个兴趣小组的概率依次为,已知三个兴趣小组他都能进入的概率为,至少进入一个兴趣小组的概率为,且.
(1)求与的值;
(2)该校根据兴趣小组活动安排情况,对进入“绘画”兴趣小组的同学增加校本选修学分1分,对进入“书法”兴趣小组的同学增加校本选修学分2分,对进入“诗词”兴趣小组的同学增加校本选修学分3分.求该同学在兴趣小组方面获得校本选修学分分数不低于4分的概率.
18.(本题满分17分)
如图,四棱台中,上、下底面均是正方形,且侧面是全等的等腰梯形,分别为DC,BC的中点,上下底面中心的连线垂直于上下底面,且与侧棱所在直线所成的角为.
(1)求证:平面;
(2)求点到平面的距离;
(3)在线段上是否存在点,使得直线与平面所成的角为,若存在,求出线段BM的长;若不存在,请说明理由.
19.(本题满分17分)
已知动点M与两个定点的距离的比为,记动点的轨迹为曲线.
(1)求曲线的方程,并说明其形状;
(2)已知,过直线上的动点分别作曲线的两条切线PQ,为切点),连接PD交QR于点,
(ⅰ)证明:直线QR过定点,并求该定点坐标;
(ⅱ)是否存在点P,使的面积最大?若存在,求出点的坐标;若不存在,请说明理由.
同课章节目录
