期中综合试题(第11章--第13章) 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 期中综合试题(第11章--第13章) 2024--2025学年上学期初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 14:53:40 | ||
图片预览


文档简介
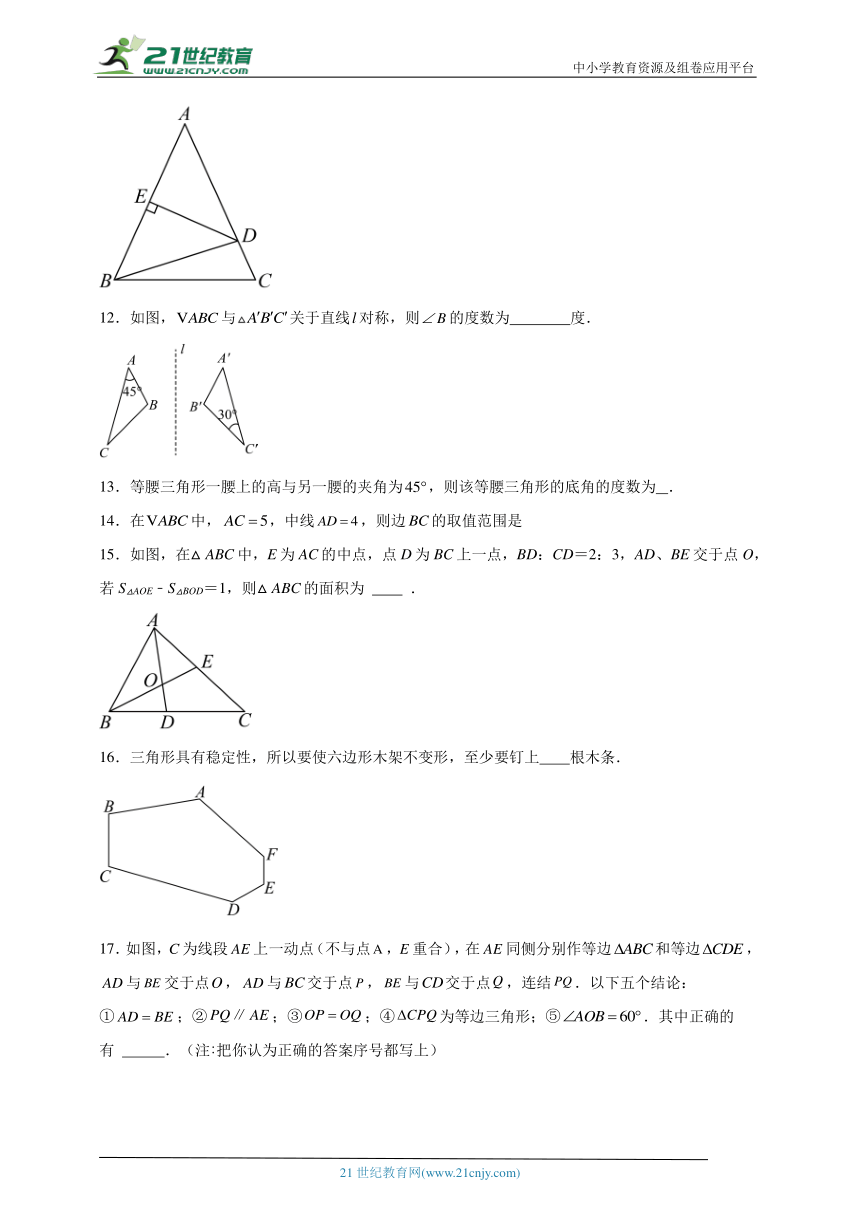
中小学教育资源及组卷应用平台
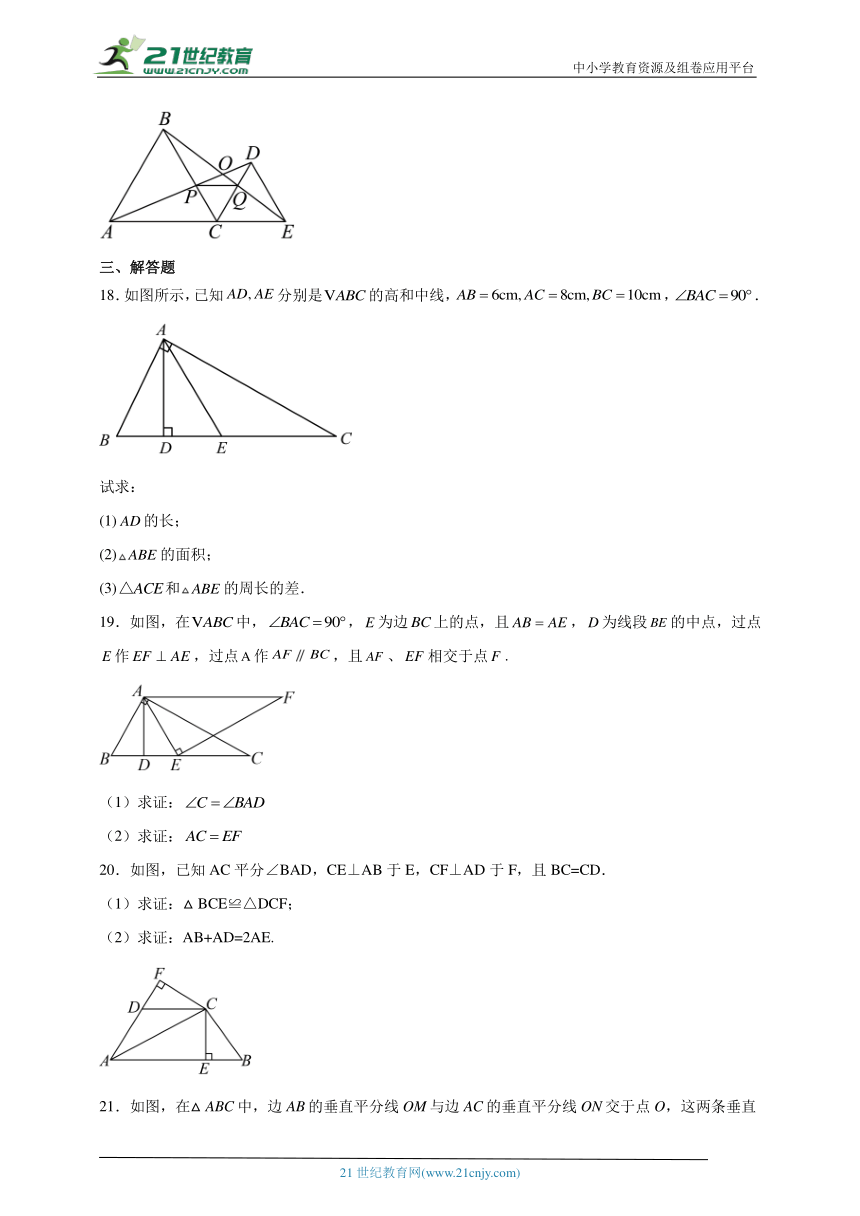
期中综合试题(第11章--第13章)
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,下列大学的校徽图案是轴对称图形的是( )
A. B. C. D.
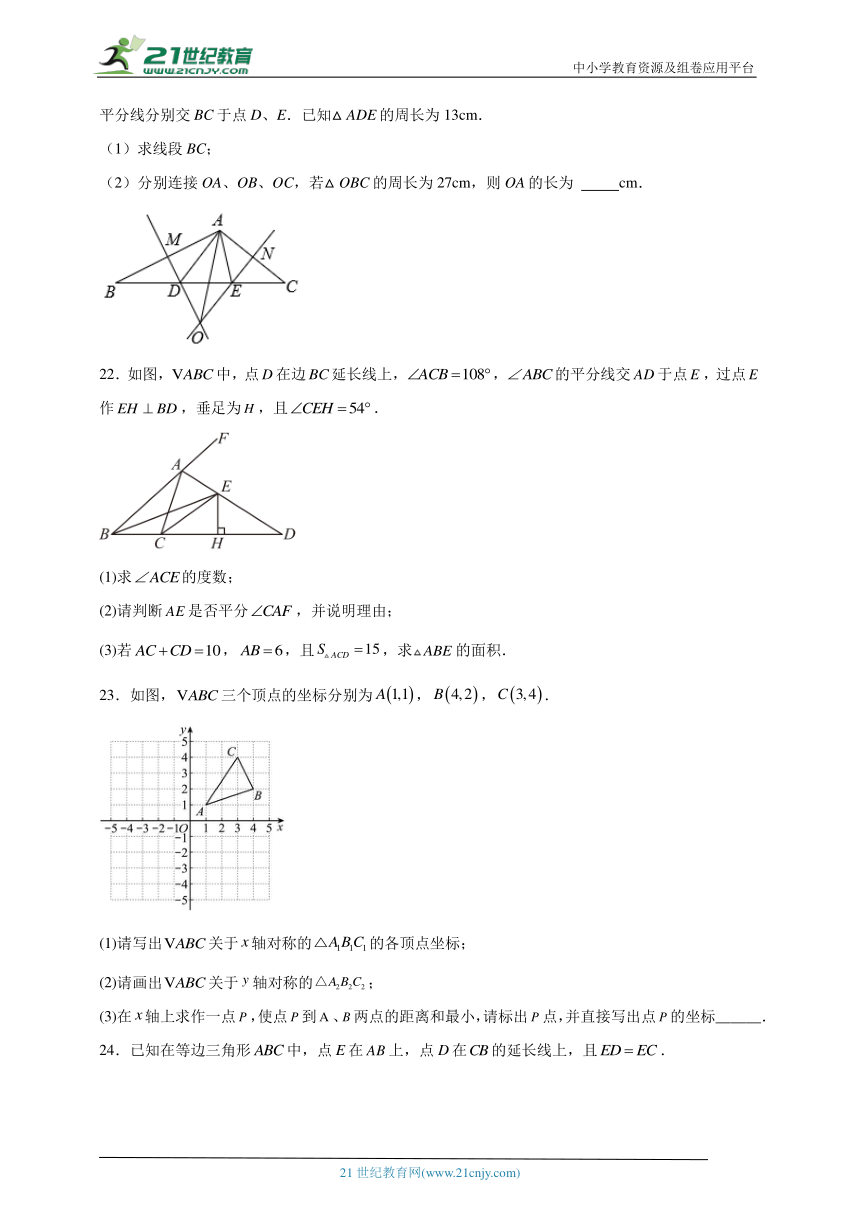
2.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形 B.都是钝角三角形
C.都是锐角三角形 D.是一个直角三角形和一个钝角三角形
3.以下说法:①三角形按角分类分为锐角三角形、直角三角形和钝角三角形;②三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;③等腰三角形至少有两边相等;④等边三角形是等腰三角形.其中正确的说法是( ).
A.①②③④ B.①②③ C.①③ D.①③④
4.如图,中,,,将折叠,使得点B与点A重合,折痕分别交、于点D、E,当中有两个角相等时,的度数为( ).
A.或 B.或
C.或或 D.或或
5.下列长度的三条线段与长度为5的线段能组成四边形的是( )
A.1,1,1 B.1,1,8 C.1,2,2 D.2,2,2
6.如图,若,,,则的度数为( )
A. B. C. D.
7.如图,在中,,的平分线BD交AC于点D,若,则点D到AB的距离DE是( )
A.2cm B.3cm C.4cm D.5cm
8.如图,已知的面积为12,平分,且于点D,则的面积是( )
A.10 B.8 C.6 D.4
9.如图,在△ABC中,∠A=90°,BE是△ABC的角平分线,ED⊥BC于点D,CD=4,△CDE周长为12,则AC的长是( )
A.14 B.8 C.16 D.6
10.用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点A,O,D在同一条直线上,量出CD的长度即知小河AB的宽度.这里判断△AOB≌△DOC的依据是( )
A.SAS或SSA B.SAS或ASA C.AAS或SSS D.ASA或AAS
二、填空题
11.如图,中作的垂直平分线交于,交于,已知,若的周长为,则的周长是 .
12.如图,与关于直线对称,则的度数为 度.
13.等腰三角形一腰上的高与另一腰的夹角为,则该等腰三角形的底角的度数为 .
14.在中,,中线,则边的取值范围是
15.如图,在△ABC中,E为AC的中点,点D为BC上一点,BD:CD=2:3,AD、BE交于点O,若S△AOE﹣S△BOD=1,则△ABC的面积为 .
16.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 根木条.
17.如图,为线段上一动点(不与点,重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连结.以下五个结论:
①;②;③;④为等边三角形;⑤.其中正确的有 .(注把你认为正确的答案序号都写上)
三、解答题
18.如图所示,已知分别是的高和中线,,.
试求:
(1)的长;
(2)的面积;
(3)和的周长的差.
19.如图,在中,,为边上的点,且,为线段的中点,过点作,过点作,且、相交于点.
(1)求证:
(2)求证:
20.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
21.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为13cm.
(1)求线段BC;
(2)分别连接OA、OB、OC,若△OBC的周长为27cm,则OA的长为 cm.
22.如图,中,点在边延长线上,,的平分线交于点,过点作,垂足为,且.
(1)求的度数;
(2)请判断是否平分,并说明理由;
(3)若,,且,求的面积.
23.如图,三个顶点的坐标分别为,,.
(1)请写出关于轴对称的的各顶点坐标;
(2)请画出关于轴对称的;
(3)在轴上求作一点,使点到、两点的距离和最小,请标出点,并直接写出点的坐标______.
24.已知在等边三角形中,点E在上,点D在的延长线上,且.
(1)【特殊情况,探索结论】
如图①,当点E为的中点时,确定线段与的大小关系,请你直接写出结论:______(填“”,“ ”或“”).
(2)【特例启发,解答题目】
如图②,当点E为边上任意一点时,确定线段与的大小关系,请你直接写出结论,______(填“”,“ ”或“”).
理由如下,过点E作,交于点F(请你完成以下解答过程).
(3)【拓展结论,设计新题】
在等边三角形中,点E在直线上,点D在的延长线上,且,若的边长为1,,求的长(请你画出相应图形,并直接写出结果).
参考答案:
1.A
解:A.是轴对称图形,故本选项符合题意;
B.不是轴对称图形,故本选项不符合题意;
C.不是轴对称图形,故本选项不符合题意;
D.不是轴对称图形,故本选项不符合题意.
2.C
如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角互补,故这两个三角形不可能都是锐角三角形.
3.D
解:三角形按角分为锐角三角形、直角三角形和钝角三角形,故①说法正确;
三角形按边分为等腰三角形和不等边三角形,故②说法错误;
等腰三角形要么有两边相等要么三边都相等,等腰三角形至少有两边相等,故③说法正确;
等边三角形是特殊的等腰三角形,所以等边三角形是等腰三角形,故④说法正确.
4.D
解:由折叠的性质知:,
①当,
∴;
②当,
则,
∴;
③当,
则,
∴.
5.D
A、1+1+1<5,即这三条线段的和小于5,根据两点间距离最短即知,此选项错误;
B、1+1+5<8,即这三条线段的和小于8,根据两点间距离最短即知,此选项错误;
C、1+2+2=5,即这三条线段的和等于5,根据两点间距离最短即知,此选项错误;
D、2+2+2>5,即这三条线段的和大于5,根据两点间距离最短即知,此选项正确;
6.B
解:∵∠B=60°,∠C=40°,
∴∠BAC=180°-60°-40°=80°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=80°,
∴∠EAC=∠DAE-∠DAC=80°-35°=45°.
7.C
解:∵的平分线BD交AC于点D,,DE⊥AB,
∴,
8.C
解:延长交与点E,
∵平分,且于点D,
∴,
∵,
∴,
∴,,
∴是的中线,
∴,
∵的面积为12,且,
则的面积是,
9.B
解:∵BE是△ABC的角平分线,ED⊥BC,∠A=90°,
∴AE=DE,
∵△CDE的周长为12,CD=4,
∴DE+EC=8,
∴AC=AE+EC=8,
10.D
解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
在△AOB和△DOC中,,
∴△AOB≌△DOC(ASA),
方法二:
∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠AOB=∠COD,∠AOB+∠BAO=90°,∠COD+∠CDO=90°,
∴∠BAO=∠CDO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
11.
解:垂直平分,
,,
,
的周长,
的周长为,
,
的周长为.
故答案为:.
12.
解:与关于直线对称,
,
.
故答案为:.
13.或
解:分两种情况讨论:
若,如图所示:
,
,
,
,
,
;
若,如图所示:
同可得:,
,
,
;
综上所述:等腰三角形底角的度数为或.
故答案为或.
14.
解:在中,,,
,
是的中线,
∴,
.
故答案为:.
15.10
解:∵点E为AC的中点,
∴S△ABE=S△ABC.
∵BD:CD=2:3,
∴S△ABD=S△ABC,
∵S△AOE﹣S△BOD=1,S△AOE﹣S△BOD=,
∴S△ABC﹣S△ABC=1,
解得S△ABC=10.
故答案为:10.
16.3
解:过六边形的一个顶点作对角线,有条对角线,
所以至少要钉上根木条.
故答案为.
17.①②④⑤
解:和都是等边三角形,
,,,
,
,
在和中,
,,,
,
,结论①正确.
∵,
,
又,
,
,
在和中,
,,,
,
,,
又,
为等边三角形,结论④正确;
,
,结论②正确.
,
,
,
结论⑤正确.
没有条件证出,③错误;
综上,可得正确的结论有4个:①②④⑤.
故答案为:①②④⑤.
18.(1)
(2)
(3)
(1)解:,是边上的高,
,
,
即的长度为;
(2)解:如图,是直角三角形,,,,
.
又是边的中线,
.
的面积是.
(3)解:为边上的中线,
,
的周长的周长,
即和的周长的差是.
19.(1)见解析;(2)见解析
(1)如图
∵,
∴是等腰三角形
又∵为的中点,
∴(等腰三角形三线合一)
在和中,
∵为公共角,,
∴.
另解:∵为的中点,
∵,又,,
∴,
∴,又,
∴
∴,
在和中,
∵为公共角,,
∴.
(2)∵,
∴,
∵,
∴,
∴,
又∵,
∴,
∴.
20.详见解析
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
21.(1)13cm;(2)7cm
解:(1)边AB的垂直平分线OM,
,
同理,
;
(2)垂直平分,
,
同理,
,
又的周长为,,
,
,
,
故答案是:7cm.
22.(1)
(2)平分,理由见解析
(3)的面积为9
(1)解:,
,
,
,
,
,
;
(2)解:平分,理由如下:
过点分别作于,与,
平分,
,
,
平分,
,
,
平分;
(3)解:,,,
,
即,
解得,
,
.
23.(1)点,,
(2)见解析
(3)
(1)解:与关于轴对称,
点,,.
(2)如图,即为所求.
(3)如图,点即为所求,
点的坐标为.
故答案为:.
24.(1)
(2),见解析
(3),画图见解析.
(1)解:∵在等边三角形中,,且E是中点,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
故答案为:;
(2)解:,理由如下:
如图所示,过点作,交于点,
则,,,
是等边三角形,
,,
,,
为等边三角形,,
, ,
,
,
,
在和中,
,
,
,
;
(3)解:∵等边的边长为1,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中综合试题(第11章--第13章)
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.“致中和,天地位焉,万物育焉.”对称美是我国古人和谐平衡思想的体现,下列大学的校徽图案是轴对称图形的是( )
A. B. C. D.
2.将一个三角形纸片剪开分成两个三角形,这两个三角形不可能( )
A.都是直角三角形 B.都是钝角三角形
C.都是锐角三角形 D.是一个直角三角形和一个钝角三角形
3.以下说法:①三角形按角分类分为锐角三角形、直角三角形和钝角三角形;②三角形按边分类可分为等腰三角形、等边三角形和三边都不相等的三角形;③等腰三角形至少有两边相等;④等边三角形是等腰三角形.其中正确的说法是( ).
A.①②③④ B.①②③ C.①③ D.①③④
4.如图,中,,,将折叠,使得点B与点A重合,折痕分别交、于点D、E,当中有两个角相等时,的度数为( ).
A.或 B.或
C.或或 D.或或
5.下列长度的三条线段与长度为5的线段能组成四边形的是( )
A.1,1,1 B.1,1,8 C.1,2,2 D.2,2,2
6.如图,若,,,则的度数为( )
A. B. C. D.
7.如图,在中,,的平分线BD交AC于点D,若,则点D到AB的距离DE是( )
A.2cm B.3cm C.4cm D.5cm
8.如图,已知的面积为12,平分,且于点D,则的面积是( )
A.10 B.8 C.6 D.4
9.如图,在△ABC中,∠A=90°,BE是△ABC的角平分线,ED⊥BC于点D,CD=4,△CDE周长为12,则AC的长是( )
A.14 B.8 C.16 D.6
10.用如图所示方法测小河宽度:AB⊥BC,OB=OC,BC⊥CD,点A,O,D在同一条直线上,量出CD的长度即知小河AB的宽度.这里判断△AOB≌△DOC的依据是( )
A.SAS或SSA B.SAS或ASA C.AAS或SSS D.ASA或AAS
二、填空题
11.如图,中作的垂直平分线交于,交于,已知,若的周长为,则的周长是 .
12.如图,与关于直线对称,则的度数为 度.
13.等腰三角形一腰上的高与另一腰的夹角为,则该等腰三角形的底角的度数为 .
14.在中,,中线,则边的取值范围是
15.如图,在△ABC中,E为AC的中点,点D为BC上一点,BD:CD=2:3,AD、BE交于点O,若S△AOE﹣S△BOD=1,则△ABC的面积为 .
16.三角形具有稳定性,所以要使六边形木架不变形,至少要钉上 根木条.
17.如图,为线段上一动点(不与点,重合),在同侧分别作等边和等边,与交于点,与交于点,与交于点,连结.以下五个结论:
①;②;③;④为等边三角形;⑤.其中正确的有 .(注把你认为正确的答案序号都写上)
三、解答题
18.如图所示,已知分别是的高和中线,,.
试求:
(1)的长;
(2)的面积;
(3)和的周长的差.
19.如图,在中,,为边上的点,且,为线段的中点,过点作,过点作,且、相交于点.
(1)求证:
(2)求证:
20.如图,已知AC平分∠BAD,CE⊥AB于E,CF⊥AD于F,且BC=CD.
(1)求证:△BCE≌△DCF;
(2)求证:AB+AD=2AE.
21.如图,在△ABC中,边AB的垂直平分线OM与边AC的垂直平分线ON交于点O,这两条垂直平分线分别交BC于点D、E.已知△ADE的周长为13cm.
(1)求线段BC;
(2)分别连接OA、OB、OC,若△OBC的周长为27cm,则OA的长为 cm.
22.如图,中,点在边延长线上,,的平分线交于点,过点作,垂足为,且.
(1)求的度数;
(2)请判断是否平分,并说明理由;
(3)若,,且,求的面积.
23.如图,三个顶点的坐标分别为,,.
(1)请写出关于轴对称的的各顶点坐标;
(2)请画出关于轴对称的;
(3)在轴上求作一点,使点到、两点的距离和最小,请标出点,并直接写出点的坐标______.
24.已知在等边三角形中,点E在上,点D在的延长线上,且.
(1)【特殊情况,探索结论】
如图①,当点E为的中点时,确定线段与的大小关系,请你直接写出结论:______(填“”,“ ”或“”).
(2)【特例启发,解答题目】
如图②,当点E为边上任意一点时,确定线段与的大小关系,请你直接写出结论,______(填“”,“ ”或“”).
理由如下,过点E作,交于点F(请你完成以下解答过程).
(3)【拓展结论,设计新题】
在等边三角形中,点E在直线上,点D在的延长线上,且,若的边长为1,,求的长(请你画出相应图形,并直接写出结果).
参考答案:
1.A
解:A.是轴对称图形,故本选项符合题意;
B.不是轴对称图形,故本选项不符合题意;
C.不是轴对称图形,故本选项不符合题意;
D.不是轴对称图形,故本选项不符合题意.
2.C
如图,沿三角形一边上的高剪开即可得到两个直角三角形.
如图,钝角三角形沿虚线剪开即可得到两个钝角三角形.
如图,直角三角形沿虚线剪开即可得到一个直角三角形和一个钝角三角形.
因为剪开的边上的两个角互补,故这两个三角形不可能都是锐角三角形.
3.D
解:三角形按角分为锐角三角形、直角三角形和钝角三角形,故①说法正确;
三角形按边分为等腰三角形和不等边三角形,故②说法错误;
等腰三角形要么有两边相等要么三边都相等,等腰三角形至少有两边相等,故③说法正确;
等边三角形是特殊的等腰三角形,所以等边三角形是等腰三角形,故④说法正确.
4.D
解:由折叠的性质知:,
①当,
∴;
②当,
则,
∴;
③当,
则,
∴.
5.D
A、1+1+1<5,即这三条线段的和小于5,根据两点间距离最短即知,此选项错误;
B、1+1+5<8,即这三条线段的和小于8,根据两点间距离最短即知,此选项错误;
C、1+2+2=5,即这三条线段的和等于5,根据两点间距离最短即知,此选项错误;
D、2+2+2>5,即这三条线段的和大于5,根据两点间距离最短即知,此选项正确;
6.B
解:∵∠B=60°,∠C=40°,
∴∠BAC=180°-60°-40°=80°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=80°,
∴∠EAC=∠DAE-∠DAC=80°-35°=45°.
7.C
解:∵的平分线BD交AC于点D,,DE⊥AB,
∴,
8.C
解:延长交与点E,
∵平分,且于点D,
∴,
∵,
∴,
∴,,
∴是的中线,
∴,
∵的面积为12,且,
则的面积是,
9.B
解:∵BE是△ABC的角平分线,ED⊥BC,∠A=90°,
∴AE=DE,
∵△CDE的周长为12,CD=4,
∴DE+EC=8,
∴AC=AE+EC=8,
10.D
解:∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
在△AOB和△DOC中,,
∴△AOB≌△DOC(ASA),
方法二:
∵AB⊥BC,BC⊥CD,
∴∠ABC=∠DCB=90°,
∵∠AOB=∠COD,∠AOB+∠BAO=90°,∠COD+∠CDO=90°,
∴∠BAO=∠CDO,
在△AOB和△DOC中,
,
∴△AOB≌△DOC(AAS),
11.
解:垂直平分,
,,
,
的周长,
的周长为,
,
的周长为.
故答案为:.
12.
解:与关于直线对称,
,
.
故答案为:.
13.或
解:分两种情况讨论:
若,如图所示:
,
,
,
,
,
;
若,如图所示:
同可得:,
,
,
;
综上所述:等腰三角形底角的度数为或.
故答案为或.
14.
解:在中,,,
,
是的中线,
∴,
.
故答案为:.
15.10
解:∵点E为AC的中点,
∴S△ABE=S△ABC.
∵BD:CD=2:3,
∴S△ABD=S△ABC,
∵S△AOE﹣S△BOD=1,S△AOE﹣S△BOD=,
∴S△ABC﹣S△ABC=1,
解得S△ABC=10.
故答案为:10.
16.3
解:过六边形的一个顶点作对角线,有条对角线,
所以至少要钉上根木条.
故答案为.
17.①②④⑤
解:和都是等边三角形,
,,,
,
,
在和中,
,,,
,
,结论①正确.
∵,
,
又,
,
,
在和中,
,,,
,
,,
又,
为等边三角形,结论④正确;
,
,结论②正确.
,
,
,
结论⑤正确.
没有条件证出,③错误;
综上,可得正确的结论有4个:①②④⑤.
故答案为:①②④⑤.
18.(1)
(2)
(3)
(1)解:,是边上的高,
,
,
即的长度为;
(2)解:如图,是直角三角形,,,,
.
又是边的中线,
.
的面积是.
(3)解:为边上的中线,
,
的周长的周长,
即和的周长的差是.
19.(1)见解析;(2)见解析
(1)如图
∵,
∴是等腰三角形
又∵为的中点,
∴(等腰三角形三线合一)
在和中,
∵为公共角,,
∴.
另解:∵为的中点,
∵,又,,
∴,
∴,又,
∴
∴,
在和中,
∵为公共角,,
∴.
(2)∵,
∴,
∵,
∴,
∴,
又∵,
∴,
∴.
20.详见解析
(1)证明:∵AC是角平分线,CE⊥AB于E,CF⊥AD于F,
∴CE=CF,∠F=∠CEB=90°,
在Rt△BCE和Rt△DCF中,
∴△BCE≌△DCF;
(2)解:∵CE⊥AB于E,CF⊥AD于F,
∴∠F=∠CEA=90°,
在Rt△FAC和Rt△EAC中,,
∴Rt△FAC≌Rt△EAC,
∴AF=AE,
∵△BCE≌△DCF,
∴BE=DF,
∴AB+AD=(AE+BE)+(AF﹣DF)=AE+BE+AE﹣DF=2AE.
21.(1)13cm;(2)7cm
解:(1)边AB的垂直平分线OM,
,
同理,
;
(2)垂直平分,
,
同理,
,
又的周长为,,
,
,
,
故答案是:7cm.
22.(1)
(2)平分,理由见解析
(3)的面积为9
(1)解:,
,
,
,
,
,
;
(2)解:平分,理由如下:
过点分别作于,与,
平分,
,
,
平分,
,
,
平分;
(3)解:,,,
,
即,
解得,
,
.
23.(1)点,,
(2)见解析
(3)
(1)解:与关于轴对称,
点,,.
(2)如图,即为所求.
(3)如图,点即为所求,
点的坐标为.
故答案为:.
24.(1)
(2),见解析
(3),画图见解析.
(1)解:∵在等边三角形中,,且E是中点,
∴,
∵,
∴,
∴,
∴,
∴,
∴;
故答案为:;
(2)解:,理由如下:
如图所示,过点作,交于点,
则,,,
是等边三角形,
,,
,,
为等边三角形,,
, ,
,
,
,
在和中,
,
,
,
;
(3)解:∵等边的边长为1,,
∴,
∴,
∵,
∴,
∵,
∴,
∴,
∴,
∴,
∴.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
