必修一3.3指数函数的性质

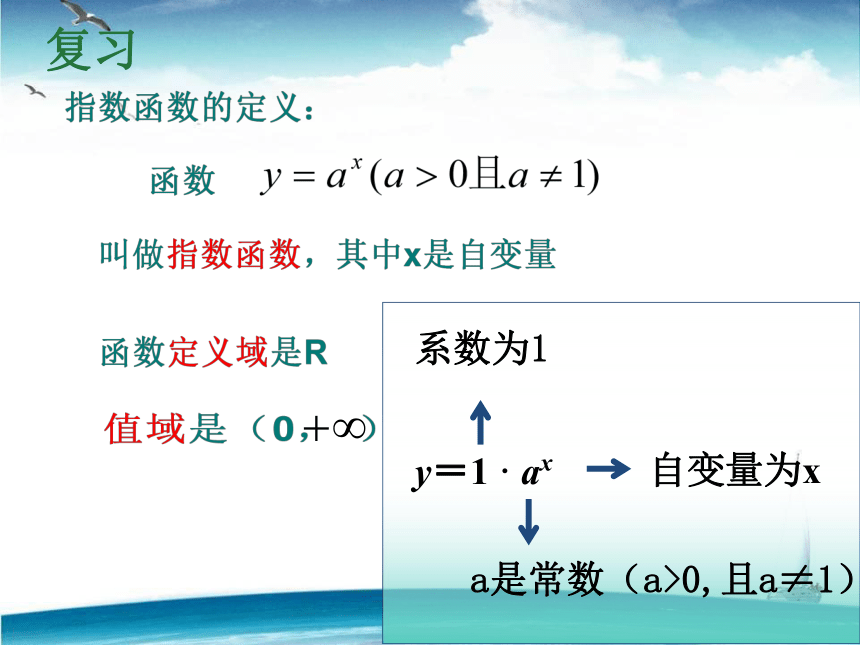
课件17张PPT。复习指 数 函 数 图 象 特 征 1指 数 函 数 图 象 特 征 §3.2 指数函数的图像和性质教学目标：
1、理解和掌握指数函数的图象和性质；
2、归纳指数函数底数a 对图象的影响；
3、归纳底数a对指数函数单调性的影响，并利用它熟练比较几个指数幂的大小
4、体会一般数学讨论方法及数形结合的思想；
重点、难点：
重点：
（1）指数函数的概念和性质及其应用.
（2）利用指数函数单调性熟练比较几个指数幂的大小
难点：
利用函数单调性比较指数幂的大小（即性质的应用）.
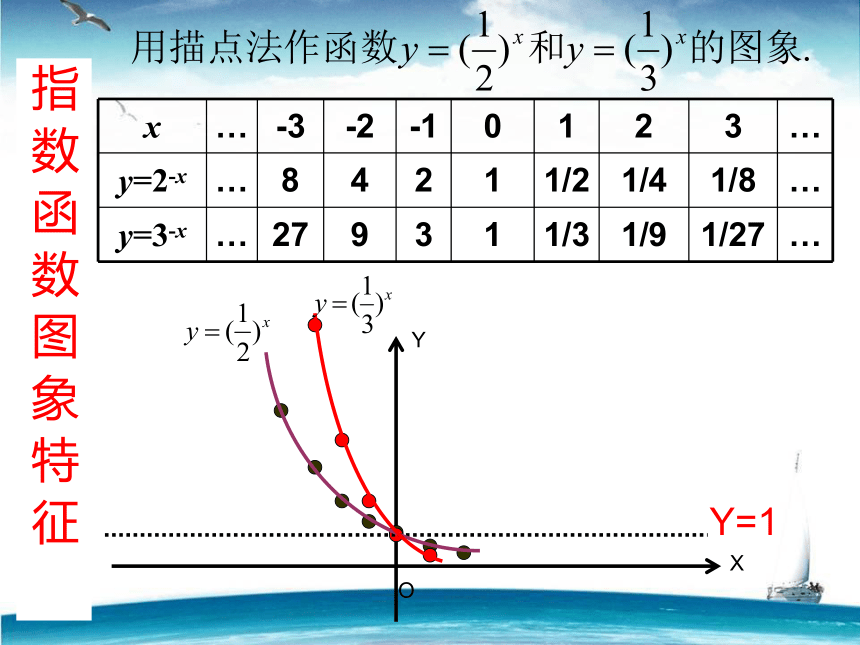
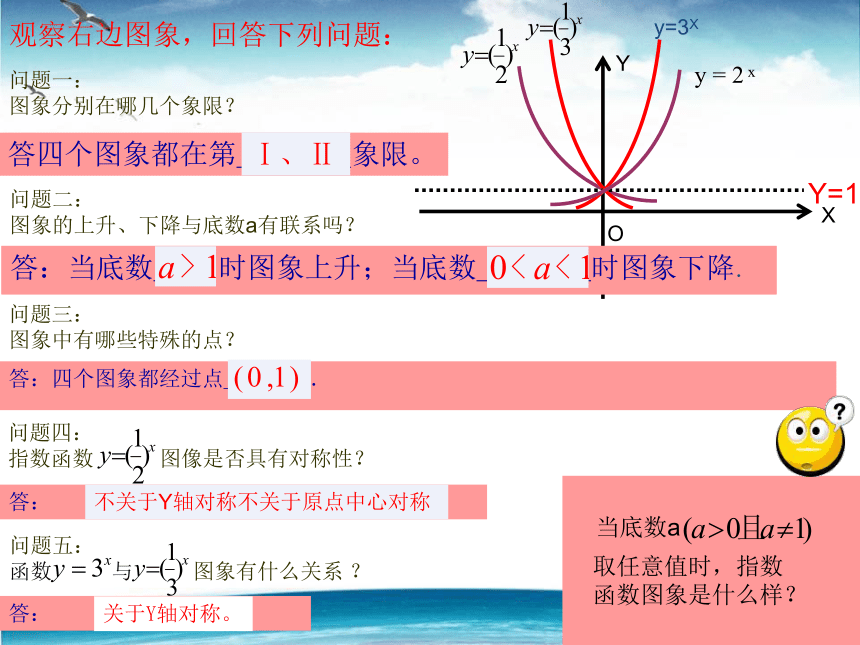
答：观察右边图象，回答下列问题：问题一：
图象分别在哪几个象限？问题二：
图象的上升、下降与底数a有联系吗？问题三：
图象中有哪些特殊的点？答四个图象都在第＿＿＿＿象限。答：当底数＿＿ 时图象上升；当底数＿＿＿＿时图象下降．答：四个图象都经过点＿＿＿＿．Ⅰ、Ⅱ问题四：
指数函数 图像是否具有对称性？不关于Y轴对称不关于原点中心对称问题五：
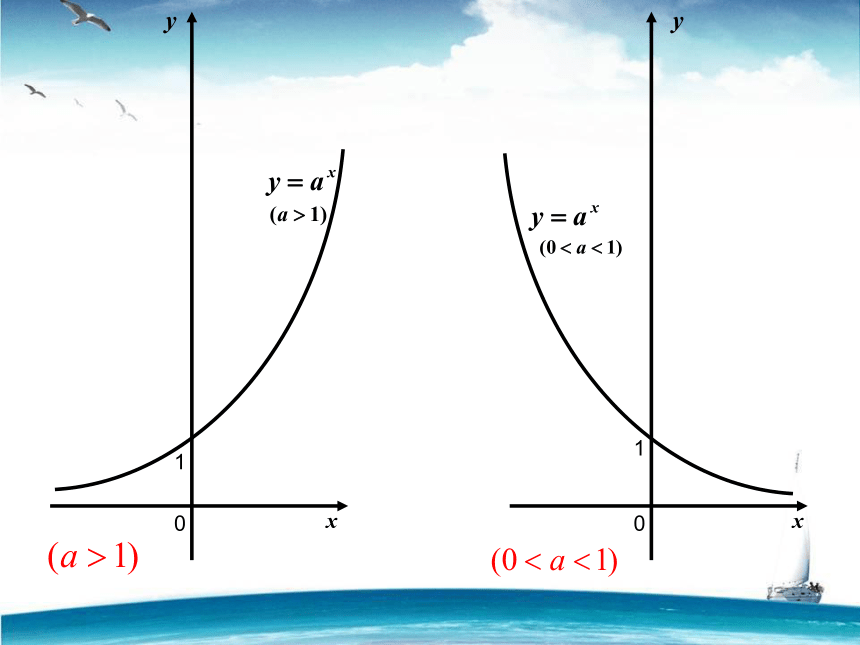
函数 与 图象有什么关系 ？答：关于Y轴对称。指数函数的图象和性质1.图象全在 上方，与 轴无限接近.1.定义域为 ，值域为2.图象过定点2.即当x=0时，3.自左向右3.自左向右3.在R上是
3.在R上是4.图象分布在左下和右上两个区域内4.图象分布在左上和右下两个区域内4.当x>0时,
当x<0时,4.当x>0时,
当x<0时, 非奇非偶函数不关于 对称,不关于 对称x轴x（0,1）图象逐渐上升图象逐渐下降Y轴原点中心增函数减函数y>1;00y>1;y=1R(0,+?).例1、比较下列各题中两个值的大小：①，解 ：利用函数单调性,与的底数是1.7，因为1.7>1，所以函数y=在R上是增函数，<；当x=2.5和3时的函数值；它们可以看成函数 y=而2.5<3，所以， ②， 解：利用函数单调性与的底数是0.8，它们可以看成函数 y= 当x=-0.1和-0.2时的函数值； 因为0<0.8<1，所以函数y=在R是减函数， 而-0.1>-0.2，所以， < ③，解 ：根据指数函数的性质，
由图像得，且>从而有或者练习：1、已知下列不等式，试比较m、n的大小：2、比较下列各数的大小： 比较指数型值常常借助于指数函数的图像或直接利用函数的单调性或选取适当的中介值（常用的特殊值是0和1），再利用单调性比较大小例2、课本P72页例2
我们一起仔细思考下例题的解题思路
提高练习1、求函数的定义域：2、函数y=ax(a>0且a≠1)在[0,1]上的最大值与最小值的和为3,求a的值. 若两个指数函数的底数互为倒数，则两个函数的图象关于y轴对称探讨思考:函数 的图象和函数 有什么关系？可否利用 的图象画出 的图象？
问题五：
函数 与 图象有什么关系 ？答：关于Y轴对称。小结： 函数叫做指数函数，其中x是自变量，函数定义域是R。1.指数函数的定义： 2.指数函数的的图象和性质： 方法:利用函数图像研究函数性质是一种直观而形象的
方法，记忆指数函数性质时可以联想指数函数的图像。 高考链接：例1、函数 的值域是（ ）
A. B.
C. D.
例2、若 ，则a,b,c的大小关系是( ）
A.a>b>c B.aC.a对这一节的内容
进行熟记和练习