物理人教版(2019)选择性必修第一册 1.1动量(共15张ppt)
文档属性
| 名称 | 物理人教版(2019)选择性必修第一册 1.1动量(共15张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 24.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-07 10:30:27 | ||
图片预览





文档简介
(共15张PPT)
第一章 动量守恒定律
第1节 动量
问题导入
用两根长度相同的线绳,分别悬挂两个完全相同的钢球A、B,且两球并排放置。拉起A球,然后放开,该球与静止的B球发生碰撞。可以看到,碰撞后A球停止运动而静止,B球开始运动,最终摆到和A球拉起时同样的高度。为什么会发生这样的现象呢
一、寻求碰撞中的不变量
质量不同小球的碰撞
结论:两个物体碰撞前后的速度都会发生变化,物体的质量不同时速度变化的情况也不一样。
那么,碰撞前后那个物理量是不变的?
猜想1:动能不变
猜想2:质量与速度乘积和不变
1.实验猜想
2.实验验证
次数 m1/kg m2/kg v/(m.s-1) v'/(m.s-1)
1 0.519 0.519 0.628 0.307
2 0.519 0.718 0.656 0.265
3 0.718 0.519 0.572 0.321
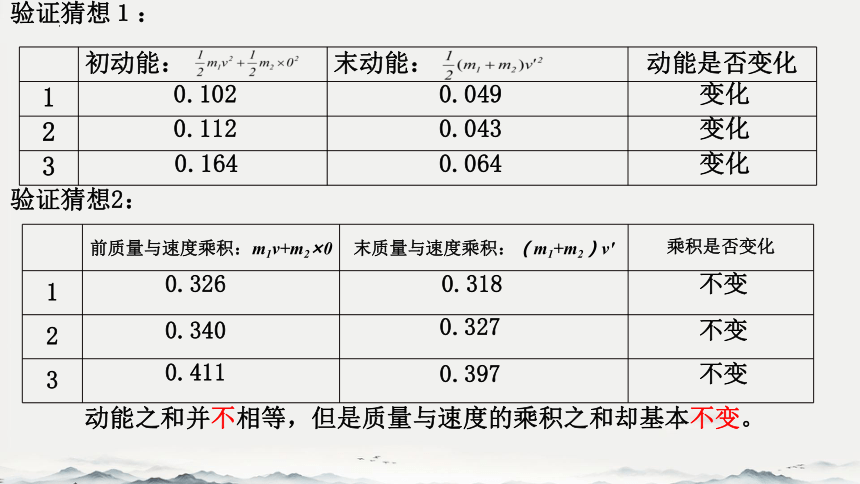
验证猜想1:
初动能: 末动能: 动能是否变化
1
2
3
0.102
0.112
0.164
0.049
变化
变化
变化
0.043
0.064
验证猜想2:
前质量与速度乘积:m1v+m2×0 末质量与速度乘积:(m1+m2)v' 乘积是否变化
1
2
3
0.326
0.340
0.411
0.318
0.327
0.397
不变
不变
不变
动能之和并不相等,但是质量与速度的乘积之和却基本不变。
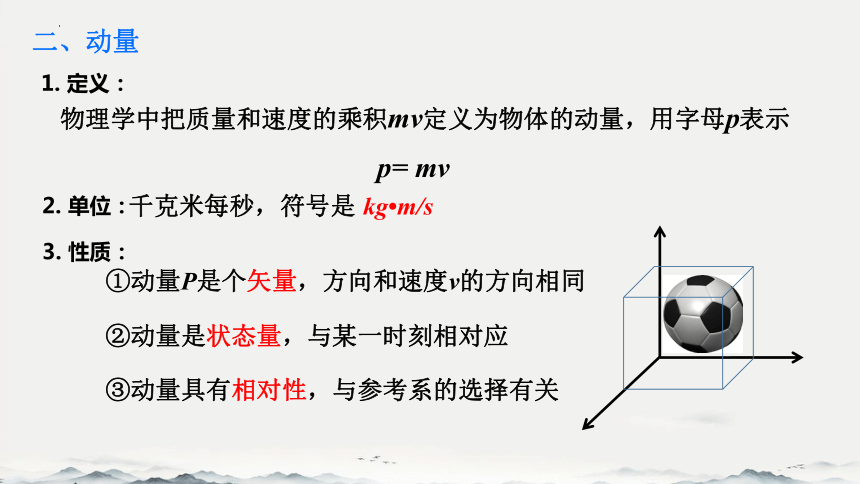
物理学中把质量和速度的乘积mv定义为物体的动量,用字母p表示
p= mv
①动量P是个矢量,方向和速度v的方向相同
②动量是状态量,与某一时刻相对应
③动量具有相对性,与参考系的选择有关
二、动量
1. 定义:
2. 单位:
3. 性质:
千克米每秒,符号是 kg m/s
例1 一个质量为0.1 kg的钢球,以6m/s的速度水平向右运动,碰到坚硬的墙壁后弹回,沿着同一直线以6m/s的速度水平向左运动。碰撞前后钢球的动量变化了多少
解:
①以小球为研究对象,取水平向右为坐标轴的正方向。
②碰前:P=mv=0.1×6=0.6kgm/s
x
o
碰撞后钢球的速度为v′=-6m/s,碰撞后钢球的动量
p′=m v′=0.1×(-6)=-0.6kgm/s,(注意负号)
③碰撞前后钢球动量的变化为:△p= p′-p=-1.2kgm/s
负号与坐标轴的方向相反,方向水平向左。
(1)定义:物体的末动量与初动量的矢量差叫做物体动量的变化。
(2)公式:Δ p = mΔ
1.动量的变化(Δ p)
通过例1,你能总结一下你计算这个例题收获了哪些知识吗?
(3)方向:动量是矢量,计算动量变化前要选择坐标轴方向,数值正负表示 p方向,方向与Δ 的方向相同。
(4)运算:如果物体沿直线运动,选定坐标轴方向后,动量运算可以简化为代数运算。
思考:如果物体不沿直线运动,动量的变化如何计算?
【例2】如图所示,一个质量是0.2kg的钢球,以v=20m/s的速度斜射到坚硬的大理石板上,入射角度是37°,碰撞后被斜着弹出,弹出的角度为53°,速度变为v'=15m/s。关于碰撞过程中,下列说法正确的是
A.钢球在竖直方向的动量变化的大小为0.14kg·m/s
B.钢球在竖直方向的动量变化的大小为5kg·m/s
C.钢球总动量变化的大小为1kg·m/s
D.钢球总动量变化的大小为7kg·m/s
结论:不在同一条直线上的动量变化的运算,遵循平行四边形定则。
B
1.动量和动能都是描述物体运动过程中的某一状态。
2.动量是矢量,动能是标量。
4.动量发生变化时,动能不一定发生变化,动能发生变化时,动量一定发生变化。
3.动量与动能的定量关系:
动量发生变化
速度大小改变方向不变
速度大小不变方向改变
速度大小和方向都改变
动能改变
动能改变
动能不变
动量和动能的关系
做一做
让一位同学把一个充气到直径1.5 m左右的大乳胶气球,以某一速度水平投向你,请你接住。把气放掉后气球变得很小,再把气球以相同的速度投向你。两种情况下,你的体验有什么不同
例1:解答以下三个小题,总结动量与动能概念的不同。
(1)质量为2kg的物体,速度由3m/s増大为6m/s,它的动量和动能各增大为原来的几倍
课堂练习
解:
(1)初动量为 p0=mv0=2×3kg·m/s=6kg·m/s
末动量为 p=mv=2×6kg·m/s=12kg·m/s
2倍
初动能为
末动能为
4倍
(2)A物体质量是2kg,速度是3m/s,方向向东;B物体质量是3kg,速度是4m/s,方向向西。它们的动量的矢量和是多少?它们的动能之和是多少?
解:取向东为正方向,则B物体的速度为vB=-4m/s。两物体动量之和为
P=mAvA+mBvB=[2×3+3×(-4)]kg·m/s=-6kg·m/s
动能之和为
课堂小结
动量
公式
单位
三性
动量和动能
动量的变化
表示为:p=mv
国际单位制:千克米每秒
( kg m/s)
(1) 矢量性
(2) 瞬时性
(3) 相对性
定量关系:
(1) 公式:Δ p = mΔ
(2)方向:与Δ 的方向相同
(3)预算:代数运算或平行四边形定则
第一章 动量守恒定律
第1节 动量
问题导入
用两根长度相同的线绳,分别悬挂两个完全相同的钢球A、B,且两球并排放置。拉起A球,然后放开,该球与静止的B球发生碰撞。可以看到,碰撞后A球停止运动而静止,B球开始运动,最终摆到和A球拉起时同样的高度。为什么会发生这样的现象呢
一、寻求碰撞中的不变量
质量不同小球的碰撞
结论:两个物体碰撞前后的速度都会发生变化,物体的质量不同时速度变化的情况也不一样。
那么,碰撞前后那个物理量是不变的?
猜想1:动能不变
猜想2:质量与速度乘积和不变
1.实验猜想
2.实验验证
次数 m1/kg m2/kg v/(m.s-1) v'/(m.s-1)
1 0.519 0.519 0.628 0.307
2 0.519 0.718 0.656 0.265
3 0.718 0.519 0.572 0.321
验证猜想1:
初动能: 末动能: 动能是否变化
1
2
3
0.102
0.112
0.164
0.049
变化
变化
变化
0.043
0.064
验证猜想2:
前质量与速度乘积:m1v+m2×0 末质量与速度乘积:(m1+m2)v' 乘积是否变化
1
2
3
0.326
0.340
0.411
0.318
0.327
0.397
不变
不变
不变
动能之和并不相等,但是质量与速度的乘积之和却基本不变。
物理学中把质量和速度的乘积mv定义为物体的动量,用字母p表示
p= mv
①动量P是个矢量,方向和速度v的方向相同
②动量是状态量,与某一时刻相对应
③动量具有相对性,与参考系的选择有关
二、动量
1. 定义:
2. 单位:
3. 性质:
千克米每秒,符号是 kg m/s
例1 一个质量为0.1 kg的钢球,以6m/s的速度水平向右运动,碰到坚硬的墙壁后弹回,沿着同一直线以6m/s的速度水平向左运动。碰撞前后钢球的动量变化了多少
解:
①以小球为研究对象,取水平向右为坐标轴的正方向。
②碰前:P=mv=0.1×6=0.6kgm/s
x
o
碰撞后钢球的速度为v′=-6m/s,碰撞后钢球的动量
p′=m v′=0.1×(-6)=-0.6kgm/s,(注意负号)
③碰撞前后钢球动量的变化为:△p= p′-p=-1.2kgm/s
负号与坐标轴的方向相反,方向水平向左。
(1)定义:物体的末动量与初动量的矢量差叫做物体动量的变化。
(2)公式:Δ p = mΔ
1.动量的变化(Δ p)
通过例1,你能总结一下你计算这个例题收获了哪些知识吗?
(3)方向:动量是矢量,计算动量变化前要选择坐标轴方向,数值正负表示 p方向,方向与Δ 的方向相同。
(4)运算:如果物体沿直线运动,选定坐标轴方向后,动量运算可以简化为代数运算。
思考:如果物体不沿直线运动,动量的变化如何计算?
【例2】如图所示,一个质量是0.2kg的钢球,以v=20m/s的速度斜射到坚硬的大理石板上,入射角度是37°,碰撞后被斜着弹出,弹出的角度为53°,速度变为v'=15m/s。关于碰撞过程中,下列说法正确的是
A.钢球在竖直方向的动量变化的大小为0.14kg·m/s
B.钢球在竖直方向的动量变化的大小为5kg·m/s
C.钢球总动量变化的大小为1kg·m/s
D.钢球总动量变化的大小为7kg·m/s
结论:不在同一条直线上的动量变化的运算,遵循平行四边形定则。
B
1.动量和动能都是描述物体运动过程中的某一状态。
2.动量是矢量,动能是标量。
4.动量发生变化时,动能不一定发生变化,动能发生变化时,动量一定发生变化。
3.动量与动能的定量关系:
动量发生变化
速度大小改变方向不变
速度大小不变方向改变
速度大小和方向都改变
动能改变
动能改变
动能不变
动量和动能的关系
做一做
让一位同学把一个充气到直径1.5 m左右的大乳胶气球,以某一速度水平投向你,请你接住。把气放掉后气球变得很小,再把气球以相同的速度投向你。两种情况下,你的体验有什么不同
例1:解答以下三个小题,总结动量与动能概念的不同。
(1)质量为2kg的物体,速度由3m/s増大为6m/s,它的动量和动能各增大为原来的几倍
课堂练习
解:
(1)初动量为 p0=mv0=2×3kg·m/s=6kg·m/s
末动量为 p=mv=2×6kg·m/s=12kg·m/s
2倍
初动能为
末动能为
4倍
(2)A物体质量是2kg,速度是3m/s,方向向东;B物体质量是3kg,速度是4m/s,方向向西。它们的动量的矢量和是多少?它们的动能之和是多少?
解:取向东为正方向,则B物体的速度为vB=-4m/s。两物体动量之和为
P=mAvA+mBvB=[2×3+3×(-4)]kg·m/s=-6kg·m/s
动能之和为
课堂小结
动量
公式
单位
三性
动量和动能
动量的变化
表示为:p=mv
国际单位制:千克米每秒
( kg m/s)
(1) 矢量性
(2) 瞬时性
(3) 相对性
定量关系:
(1) 公式:Δ p = mΔ
(2)方向:与Δ 的方向相同
(3)预算:代数运算或平行四边形定则
