2024年北京通州高二(上)期中数学(PDF版,含答案)
文档属性
| 名称 | 2024年北京通州高二(上)期中数学(PDF版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 5.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 00:00:00 | ||
图片预览



文档简介
通州区2024一2025学年第一学期高二年级期中质量检测
数学试卷
2024年11月
木试卷共4页,共150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答
无效.考试结束后,请将答题卡交回.
第一部分(选择题共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的
一项
(1)若直线y=kx十1与直线y=2x平行,则k=
(A)2
(B号
(C)-2
D)-司
(2)若向量a=(1,2,x),b=(-1,2,1),c=(1,2,-2)满足条件(c一a)·b=一4,则x=
(A)-4
(B)-2
(C)0
(D)2
(3)在空间直角坐标系Oxy之中,点A(1,2,4)关于坐标平面Oyz的对称点坐标为
(A)(-1,-2,-4)(B)(-1,2,4)
(C)(1,2,-4)
(D)(-1,2,-4)
(4)已知直线的方向向量与平面a的法向量分别为a=(1,0,一1),=(2,一3,2),则
(A)l∥a
(B)l⊥a
(C)l∥a或lCa
(D)1,a相交但不垂直
(5)法向量为=(1,0,1)的平面&内有一点A(一1,1,0),则平面外点P(1,1,0)到平面α的距
离为
(A)1
(B)2
(C2
(D)W2
(6)过点(一4,2√3)作圆C:x2+y2+4x=0的两条切线,则这两条切线的夹角为
(A)
(B)
(C)
(w号
(7)圆C:x2+y2一2x=0和圆C2:x2十y2一4y=0的位置关系是
(A)相离
(B)相交
(C)外切
(D)内切
(8)如图,在平行六面体ABCD-A1B,C,D,中,AC与BD的交点为M,
若MC-xAB+yAD+xAA,则x十y十x=
B
(A)-2
8)-
D
(D)2
高二数学试卷第1页(共4页)
(9)如果A·B·C≠0,那么“A·C0”是“直线Ax十By十C=0不通过第三象限”的
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
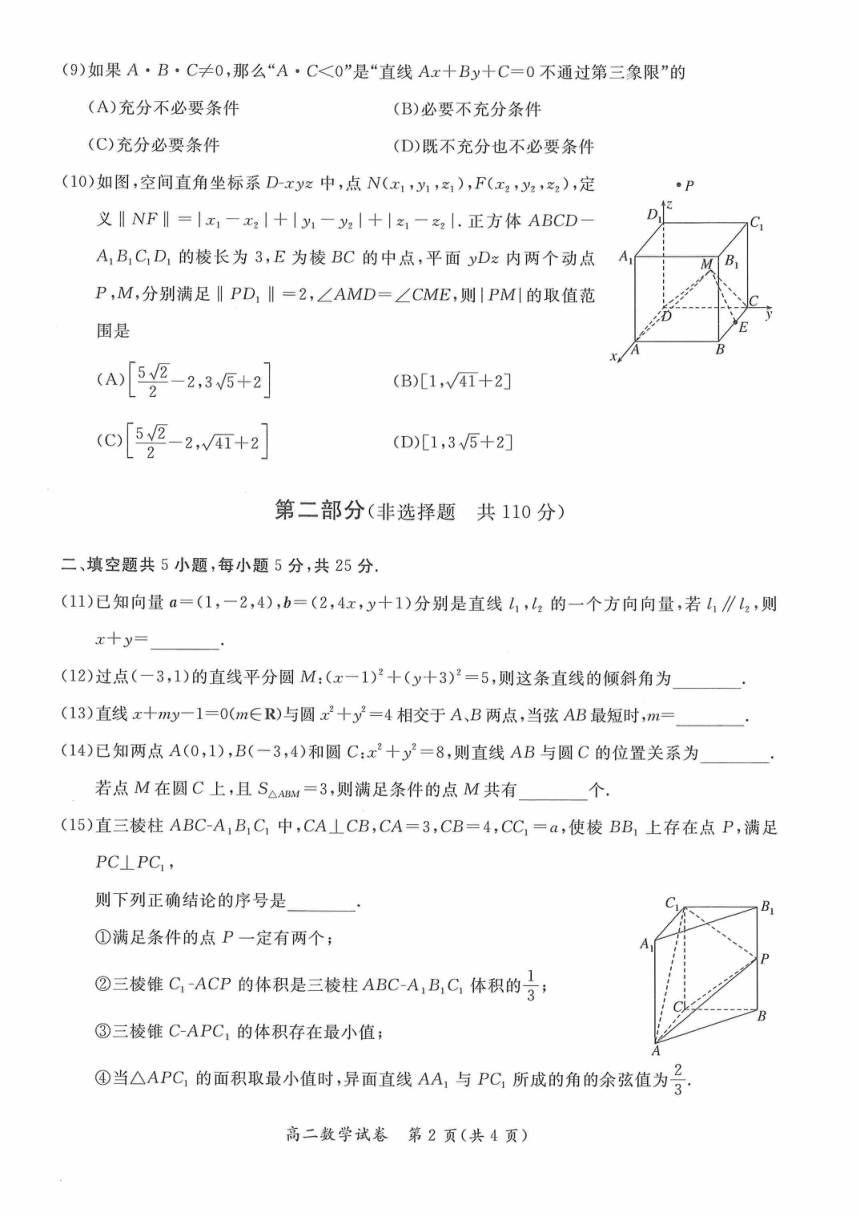
(10)如图,空间直角坐标系D-xy之中,点N(x1,y1,名1),F(x2,y2,2),定
。P
义‖NF‖=-x|+I为一y|+|之1-I.E方体ABCD-
k
A,B,C,D,的棱长为3,E为棱BC的中点,平面yDz内两个动点
B
P,M,分别满足‖PD1‖=2,∠AMD=∠CME,则|PM的取值范
围是
B
(A5
2-2,35+2
(B)[1,√41+2]
[52-2+2】
(D)[1,3√5+2]
第二部分(非选择题共110分)
二、填空题共5小题,每小题5分,共25分,
(11)已知向量a=(1,一2,4),b=(2,4.x,y+1)分别是直线1,2的一个方向向量,若L1∥12,则
x十y=
(12)过点(-3,1)的直线平分圆M:(x一1)2+(y十3)2=5,则这条直线的倾斜角为
(13)直线x十y一1=0(m∈R)与圆x2十y=4相交于A、B两点,当弦AB最短时,=
(14)已知两点A(0,1),B(一3,4)和圆C:x2+y=8,则直线AB与圆C的位置关系为
若点M在圆C上,且S△sw=3,则满足条件的点M共有
个,
(15)直三棱柱ABCA1B1C1巾,CA⊥CB,CA=3,CB=4,CC,=a,使棱BB,上存在点P,满足
PC⊥PC,
则下列正确结论的序号是
C
①满足条件的点P一定有两个;
②三楼锥C-ACP的体积是三棱柱ABC-A,B,C休积的3:
③三棱锥C-APC,的体积存在最小值;
④当△APC,的面积取最小值时,异面直线AA,与PC所成的角的余弦值为
2
高二数学试卷第2页(共4页)
数学试卷
2024年11月
木试卷共4页,共150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答
无效.考试结束后,请将答题卡交回.
第一部分(选择题共40分)
一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的
一项
(1)若直线y=kx十1与直线y=2x平行,则k=
(A)2
(B号
(C)-2
D)-司
(2)若向量a=(1,2,x),b=(-1,2,1),c=(1,2,-2)满足条件(c一a)·b=一4,则x=
(A)-4
(B)-2
(C)0
(D)2
(3)在空间直角坐标系Oxy之中,点A(1,2,4)关于坐标平面Oyz的对称点坐标为
(A)(-1,-2,-4)(B)(-1,2,4)
(C)(1,2,-4)
(D)(-1,2,-4)
(4)已知直线的方向向量与平面a的法向量分别为a=(1,0,一1),=(2,一3,2),则
(A)l∥a
(B)l⊥a
(C)l∥a或lCa
(D)1,a相交但不垂直
(5)法向量为=(1,0,1)的平面&内有一点A(一1,1,0),则平面外点P(1,1,0)到平面α的距
离为
(A)1
(B)2
(C2
(D)W2
(6)过点(一4,2√3)作圆C:x2+y2+4x=0的两条切线,则这两条切线的夹角为
(A)
(B)
(C)
(w号
(7)圆C:x2+y2一2x=0和圆C2:x2十y2一4y=0的位置关系是
(A)相离
(B)相交
(C)外切
(D)内切
(8)如图,在平行六面体ABCD-A1B,C,D,中,AC与BD的交点为M,
若MC-xAB+yAD+xAA,则x十y十x=
B
(A)-2
8)-
D
(D)2
高二数学试卷第1页(共4页)
(9)如果A·B·C≠0,那么“A·C0”是“直线Ax十By十C=0不通过第三象限”的
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
(10)如图,空间直角坐标系D-xy之中,点N(x1,y1,名1),F(x2,y2,2),定
。P
义‖NF‖=-x|+I为一y|+|之1-I.E方体ABCD-
k
A,B,C,D,的棱长为3,E为棱BC的中点,平面yDz内两个动点
B
P,M,分别满足‖PD1‖=2,∠AMD=∠CME,则|PM的取值范
围是
B
(A5
2-2,35+2
(B)[1,√41+2]
[52-2+2】
(D)[1,3√5+2]
第二部分(非选择题共110分)
二、填空题共5小题,每小题5分,共25分,
(11)已知向量a=(1,一2,4),b=(2,4.x,y+1)分别是直线1,2的一个方向向量,若L1∥12,则
x十y=
(12)过点(-3,1)的直线平分圆M:(x一1)2+(y十3)2=5,则这条直线的倾斜角为
(13)直线x十y一1=0(m∈R)与圆x2十y=4相交于A、B两点,当弦AB最短时,=
(14)已知两点A(0,1),B(一3,4)和圆C:x2+y=8,则直线AB与圆C的位置关系为
若点M在圆C上,且S△sw=3,则满足条件的点M共有
个,
(15)直三棱柱ABCA1B1C1巾,CA⊥CB,CA=3,CB=4,CC,=a,使棱BB,上存在点P,满足
PC⊥PC,
则下列正确结论的序号是
C
①满足条件的点P一定有两个;
②三楼锥C-ACP的体积是三棱柱ABC-A,B,C休积的3:
③三棱锥C-APC,的体积存在最小值;
④当△APC,的面积取最小值时,异面直线AA,与PC所成的角的余弦值为
2
高二数学试卷第2页(共4页)
同课章节目录
