甘肃省兰州市2024-2025学年高一上学期期中考试数学试题(无答案)
文档属性
| 名称 | 甘肃省兰州市2024-2025学年高一上学期期中考试数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 333.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 14:48:01 | ||
图片预览

文档简介
2024—2025学年度第一学期
高一年级数学期中试题
一、单选题(每小题6分,共40分.)
1.已知集合,,则( )
A. B. C. D.
2.已知命题:,,命题:,.则( )
A.和都是真命题 B.和都是真命题
C.和都是真命题 D.和都是真命题
3.地球表面被很厚的大气层包围,大气层的厚度大约在以上,整个大气层高度不同表现出不同的特点,分为对流层、平流层、中间层、暖层和散逸层,再上面就是星际空间了.平流层是指地面以上到的区域,下述不等式中,能表示平流层高度的是( )
A. B. C. D.
4.已知函数,且,则( )
A.1 B.2 C.3 D.6
5.已知正数、满足,不等式恒成立.则实数的取值范围是( )
A. B. C. D.
6.已知函数满足对任意实数,都有成立,则实数的取值范围是( )
A. B. C. D.
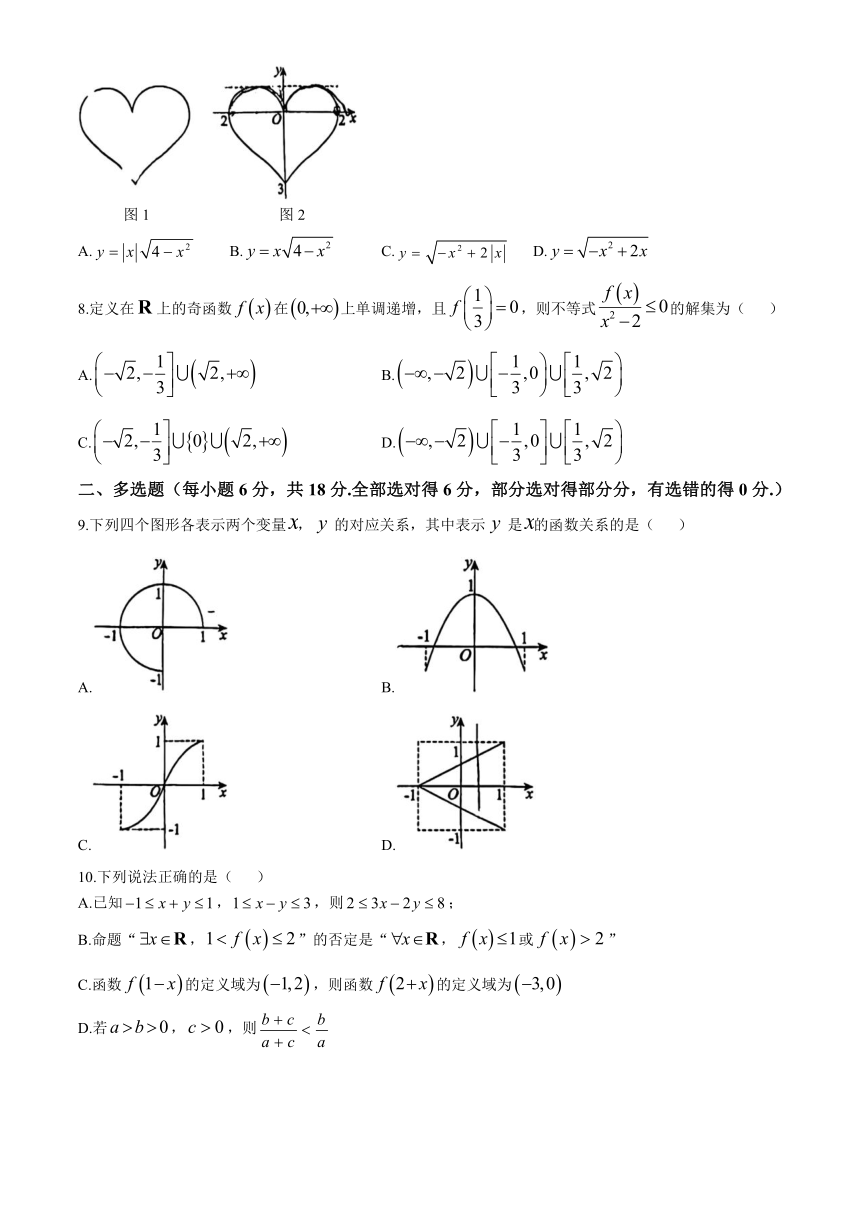
7.世界上海拔最高的天然“心形湖”位于四川省康定县的情歌木格措景区,被誉为藏在川西的“天空之心”.这个湖泊位于青藏高原,呈现出明亮的蓝绿色,水质清澈宛如明镜.湖泊周围环抱着雪山和梅花峰,景色优美迷人.下图1是这个“心形湖”的轮廓,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
图1 图2
A. B. C. D.
8.定义在上的奇函数在上单调递增,且,则不等式的解集为( )
A. B.
C. D.
二、多选题(每小题6分,共18分.全部选对得6分,部分选对得部分分,有选错的得0分.)
9.下列四个图形各表示两个变量,的对应关系,其中表示是的函数关系的是( )
A. B.
C. D.
10.下列说法正确的是( )
A.已知,,则;
B.命题“,”的否定是“,或”
C.函数的定义域为,则函数的定义域为
D.若,,则
11.已知函数的定义域为,,且当时,,则下列说法正确的处( )
A.是奇函数
B.为增函数
C.若实数满足不等式,则的取值范围为
D.
三、填空题(每小题6分,共15分.)
12.函数的定义域是______.
13.已知方程的两根一个比2大另一个比2小,则实数的范围是______.
14.俄国数学家切比雪夫是研究直线逼近函数理论的先驱.对定义在非空集合上的函数,以及函数(,),切比雪夫将函数,的最大值称为函数与的“偏差”.若(),,则函数与的“偏差”取得最小值时,的值为______.
四、解答题(本题共5小题,共77分.)
15.(13分)已知全集,集合,.
(I)当时,求,;
(2)若,求的取值范围.
(3)若是的______条件,求实数的取值集合.
请从下面两个条件中选择一个,填在上面横线中,使得的取值集合非空.
①必要不充分 ②充分不必要
16.(15分)某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理盘为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
17.(15分)已知函数是定义在上的奇函数,当时,.
(l)当时,求的解析式;
(2)判断在上的单调性,并用定义证明;
(3)若对于恒成立,求的取值范围.
18.(17分)已知函数,.
(1)若函数在上单调递减,求的取值范围.
(2)讨论函数的零点个数.
(3)解关于的不等式.
19.(17分)已知函数的图象过点,且满足.
(l)求函数的解析式;
(2)求函数在上的最大值:
(3)若满足,则称为函数的不动点.若函数有两个不相等
的不动点,,且,,求的最小值.
高一年级数学期中试题
一、单选题(每小题6分,共40分.)
1.已知集合,,则( )
A. B. C. D.
2.已知命题:,,命题:,.则( )
A.和都是真命题 B.和都是真命题
C.和都是真命题 D.和都是真命题
3.地球表面被很厚的大气层包围,大气层的厚度大约在以上,整个大气层高度不同表现出不同的特点,分为对流层、平流层、中间层、暖层和散逸层,再上面就是星际空间了.平流层是指地面以上到的区域,下述不等式中,能表示平流层高度的是( )
A. B. C. D.
4.已知函数,且,则( )
A.1 B.2 C.3 D.6
5.已知正数、满足,不等式恒成立.则实数的取值范围是( )
A. B. C. D.
6.已知函数满足对任意实数,都有成立,则实数的取值范围是( )
A. B. C. D.
7.世界上海拔最高的天然“心形湖”位于四川省康定县的情歌木格措景区,被誉为藏在川西的“天空之心”.这个湖泊位于青藏高原,呈现出明亮的蓝绿色,水质清澈宛如明镜.湖泊周围环抱着雪山和梅花峰,景色优美迷人.下图1是这个“心形湖”的轮廓,其形状如一颗爱心.图2是由此抽象出来的一个“心形”图形,这个图形可看作由两个函数的图象构成,则“心形”在轴上方的图象对应的函数解析式可能为( )
图1 图2
A. B. C. D.
8.定义在上的奇函数在上单调递增,且,则不等式的解集为( )
A. B.
C. D.
二、多选题(每小题6分,共18分.全部选对得6分,部分选对得部分分,有选错的得0分.)
9.下列四个图形各表示两个变量,的对应关系,其中表示是的函数关系的是( )
A. B.
C. D.
10.下列说法正确的是( )
A.已知,,则;
B.命题“,”的否定是“,或”
C.函数的定义域为,则函数的定义域为
D.若,,则
11.已知函数的定义域为,,且当时,,则下列说法正确的处( )
A.是奇函数
B.为增函数
C.若实数满足不等式,则的取值范围为
D.
三、填空题(每小题6分,共15分.)
12.函数的定义域是______.
13.已知方程的两根一个比2大另一个比2小,则实数的范围是______.
14.俄国数学家切比雪夫是研究直线逼近函数理论的先驱.对定义在非空集合上的函数,以及函数(,),切比雪夫将函数,的最大值称为函数与的“偏差”.若(),,则函数与的“偏差”取得最小值时,的值为______.
四、解答题(本题共5小题,共77分.)
15.(13分)已知全集,集合,.
(I)当时,求,;
(2)若,求的取值范围.
(3)若是的______条件,求实数的取值集合.
请从下面两个条件中选择一个,填在上面横线中,使得的取值集合非空.
①必要不充分 ②充分不必要
16.(15分)某企业采用新工艺,把企业生产中排放的二氧化碳转化为一种可利用的化工产品.已知该单位每月的处理量最少为400吨,最多为600吨,月处理成本(元)与月处理量(吨)之间的函数关系可近似的表示为,且每处理一吨二氧化碳得到可利用的化工产品价值为100元.
(1)该单位每月处理盘为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则国家至少需要补贴多少元才能使该单位不亏损?
17.(15分)已知函数是定义在上的奇函数,当时,.
(l)当时,求的解析式;
(2)判断在上的单调性,并用定义证明;
(3)若对于恒成立,求的取值范围.
18.(17分)已知函数,.
(1)若函数在上单调递减,求的取值范围.
(2)讨论函数的零点个数.
(3)解关于的不等式.
19.(17分)已知函数的图象过点,且满足.
(l)求函数的解析式;
(2)求函数在上的最大值:
(3)若满足,则称为函数的不动点.若函数有两个不相等
的不动点,,且,,求的最小值.
同课章节目录
