人教A版数学(选择性必修一讲义)第15讲2.1.2两条直线平行和垂直的判定(学生版+解析)
文档属性
| 名称 | 人教A版数学(选择性必修一讲义)第15讲2.1.2两条直线平行和垂直的判定(学生版+解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 00:00:00 | ||
图片预览




文档简介
第02讲 2.1.2两条直线平行和垂直的判定
课程标准 学习目标
①理解两条直线平行的条件及两条直线 垂直的条件。 ②能根据直线的斜率判断两条直线平行或垂直.。 ③能应用两条直线平行或垂直解决相关问题,理解用代数法解决几何问题.。 通过本节课的学习,理解两条直线平行与垂直的几何位置与代数运算相结合的条件与意义,能应用两直线的斜率的关系判断两直线的位置关系,并能解决与两条直线位置关系相关联的综合问题.
知识点01:两条直线平行
对于两条不重合的直线,,其斜率分别为,,有.
对两直线平行与斜率的关系要注意以下几点
(1)成立的前提条件是:
①两条直线的斜率都存在;
②与不重合.
(2)当两条直线不重合且斜率都不存在时,与的倾斜角都是,则.
(3)两条不重合直线平行的判定的一般结论是:
或,斜率都不存在.
【即学即练1】(多选)(2023·广西桂林·高二校考期中)若为两条不重合的直线,他们的倾斜角分别为,斜率分别为,则下列命题正确的是( )
A.若,则斜率 B.若斜率,则
C.若,则倾斜角 D.若倾斜角,则
【答案】ABCD
【详解】因为为两条不重合的直线,他们的倾斜角分别为,斜率分别为,
若,则斜率相等,即;又斜率是倾斜角的正切值,所以,故AC正确;
若,则,所以,故BD正确;
故选:ABCD
知识点02:两条直线垂直
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果它们的斜率之积等于,那么它们互相垂直,即.
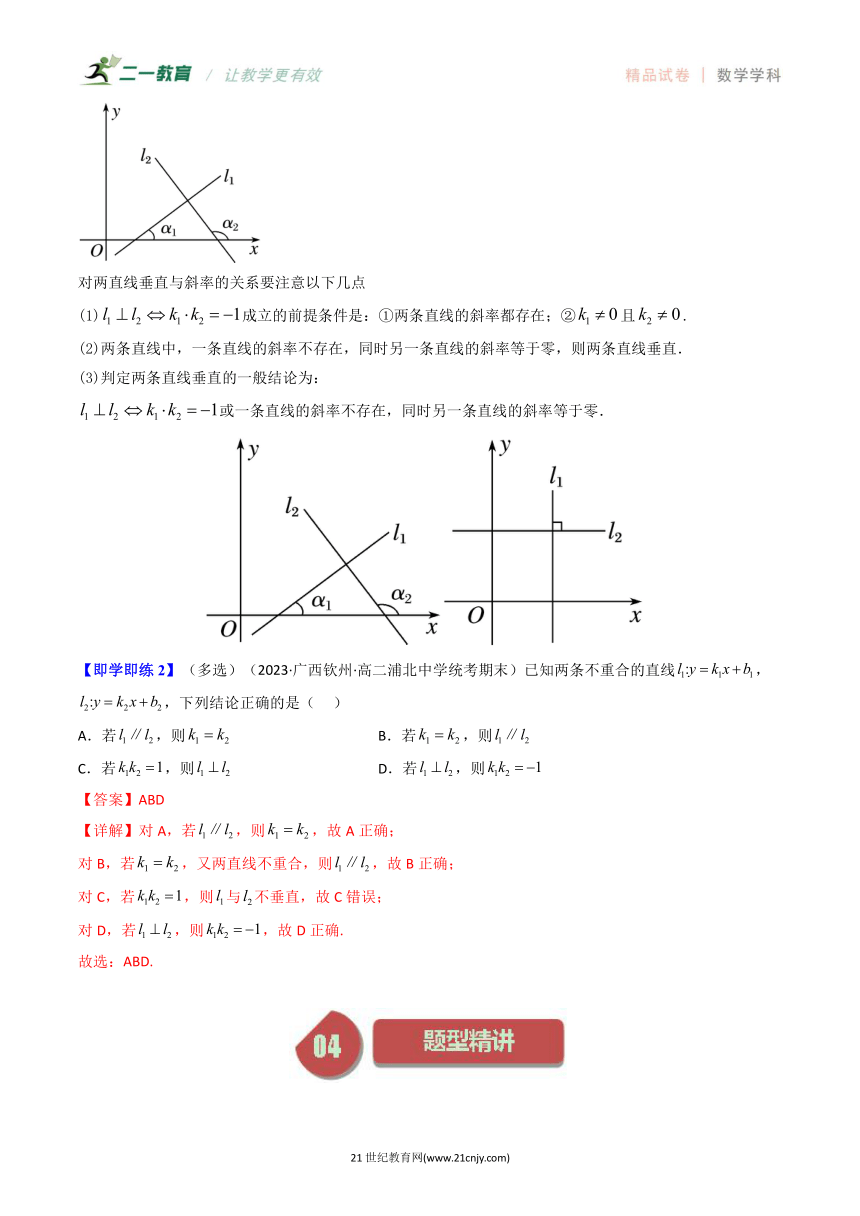
对两直线垂直与斜率的关系要注意以下几点
(1)成立的前提条件是:①两条直线的斜率都存在;②且.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【即学即练2】(多选)(2023·广西钦州·高二浦北中学统考期末)已知两条不重合的直线,,下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】ABD
【详解】对A,若,则,故A正确;
对B,若,又两直线不重合,则,故B正确;
对C,若,则与不垂直,故C错误;
对D,若,则,故D正确.
故选:ABD.
题型01 两直线平行关系的判定
【典例1】(多选)(2023春·广西柳州·高二校考阶段练习)已知直线与为两条不重合的直线,则下列命题正确的是( )
A.若,则斜率
B.若斜率,则
C.若倾斜角,则
D.若,则倾斜角
【典例2】(2023春·山东滨州·高一校考阶段练习)已知点,,,,试判定四边形的形状.
【典例3】(2023·江苏·高二假期作业)判断下列各组直线是否平行,并说明理由.
(1)经过点,经过点;
(2)的斜率为,经过点.
【变式1】(2023·江苏·高二假期作业)判断下列各题中直线与是否平行.
(1)经过点,,经过点,;
(2)经过点,,经过点,.
【变式2】(2023·全国·高二专题练习)判断下列不同的直线与是否平行.
(1)的斜率为2,经过,两点;
(2)经过,两点,平行于轴,但不经过,两点;
(3)经过,两点,经过,两点.
题型02两直线垂直关系的判定
【典例1】(2023秋·高二课时练习)以为顶点的四边形是( )
A.平行四边形,但不是矩形 B.矩形 C.梯形,但不是直角梯形 D.直角梯形
【典例2】(2023·江苏·高二假期作业)判断下列各组直线是否垂直,并说明理由.
(1)经过点经过点;
(2)经过点经过点.
【变式1】(多选)(2023春·广西柳州·高二校考阶段练习)(多选)若,,,,下面结论中正确的是( )
A. B. C. D.
【变式2】(2023·江苏·高二假期作业)已知四边形的顶点坐标为,求证:四边形为矩形.
题型03已知两直线平行关求参数
【典例1】(2023·江苏·高二假期作业)已知过和的直线与斜率为-2的直线平行,则的值是( )
A.-8 B.0 C.2 D.10
【典例2】(2022秋·四川遂宁·高二遂宁中学校考阶段练习)若直线与平行,则( )
A. B. C. D.
【典例3】(2022秋·河南濮阳·高二校考阶段练习)若直线与直线平行,直线的斜率为,则直线的倾斜角为___________.
【变式1】(2023·江苏·高二假期作业)已知直线的倾斜角为,直线的斜率为,若∥,则的值为________.
【变式2】(2022·高二课时练习)过点两点的直线与直线平行,直线的倾斜角为,则___________
题型04已知两直线垂直关求参数
【典例1】(2023·全国·高二专题练习)过点,的直线与过点,的直线垂直,则的值为( )
A. B.2 C. D.
【典例2】(2023春·甘肃兰州·高二兰州五十九中校考开学考试)已知经过点和点的直线与经过点和点的直线互相垂直,则实数的值为( )
A. B. C.或 D.或
【典例3】(2023春·黑龙江佳木斯·高二富锦市第一中学校考阶段练习)已知直线经过,两点,且直线,则直线的倾斜角为( )
A. B. C. D.
【变式1】(2023春·甘肃武威·高二民勤县第一中学校考开学考试)已知三角形三个顶点的坐标分别为,,,则边上的高的斜率为( )
A.2 B. C. D.
【变式2】(2023秋·浙江杭州·高二浙江省杭州第二中学校考期末)已知点和,点在轴上,且为直角,则点坐标为( )
A. B.或 C.或 D.
题型05直线平行、垂直在几何中的应用
【典例1】(2022秋·青海海东·高二校考期中)已知点,,,是的垂心.则点的坐标为( )
A. B. C. D.
【典例2】(2022·高二课时练习)已知点,,,,求证:四边形是梯形.
【变式1】(2022·高二课时练习)顺次连接,,),)所构成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对
【变式2】(2023·全国·高二专题练习)已知的三个顶点的坐标分别为,,,则顶点的坐标为________.
【变式3】(2023·江苏·高二假期作业)已知,,,四点,若顺次连接四点,试判断图形的形状.
A夯实基础 B能力提升
A夯实基础
1.(2023秋·广东广州·高二广州市培正中学校考期中)已知直线的倾斜角为,直线,则直线的斜率为( )
A. B. C. D.
2.(2023秋·山东泰安·高二统考期末)若直线与直线平行,则实数k的值为( )
A. B. C. D.3
3.(2023·全国·高二专题练习)下列说法中正确的是( )
A.若两条直线斜率相等,则它们互相平行
B.若,则
C.若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交
D.若两条直线的斜率都不存在,则它们相互平行
4.(2023秋·天津和平·高二天津一中校考期末)已知直线:,:,若,则实数( )
A.-2 B.-1 C.0 D.1
5.(2023春·上海长宁·高二上海市第三女子中学校考期中)“两条直线的斜率乘积为”是“两条直线互相垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
12.(2022·全国·高二专题练习)判断三点是否共线,并说明理由.
B能力提升
13.(2021春·高一课时练习)根据下列给定的条件,判断直线与直线是否平行.
(1)直线经过点,直线经过点;
(2)直线平行于y轴,直线经过点,;
(3)直线经过点,直线经过点.
第02讲 2.1.2两条直线平行和垂直的判定
课程标准 学习目标
①理解两条直线平行的条件及两条直线 垂直的条件。 ②能根据直线的斜率判断两条直线平行或垂直.。 ③能应用两条直线平行或垂直解决相关问题,理解用代数法解决几何问题.。 通过本节课的学习,理解两条直线平行与垂直的几何位置与代数运算相结合的条件与意义,能应用两直线的斜率的关系判断两直线的位置关系,并能解决与两条直线位置关系相关联的综合问题.
知识点01:两条直线平行
对于两条不重合的直线,,其斜率分别为,,有.
对两直线平行与斜率的关系要注意以下几点
(1)成立的前提条件是:
①两条直线的斜率都存在;
②与不重合.
(2)当两条直线不重合且斜率都不存在时,与的倾斜角都是,则.
(3)两条不重合直线平行的判定的一般结论是:
或,斜率都不存在.
【即学即练1】(多选)(2023·广西桂林·高二校考期中)若为两条不重合的直线,他们的倾斜角分别为,斜率分别为,则下列命题正确的是( )
A.若,则斜率 B.若斜率,则
C.若,则倾斜角 D.若倾斜角,则
【答案】ABCD
【详解】因为为两条不重合的直线,他们的倾斜角分别为,斜率分别为,
若,则斜率相等,即;又斜率是倾斜角的正切值,所以,故AC正确;
若,则,所以,故BD正确;
故选:ABCD
知识点02:两条直线垂直
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果它们的斜率之积等于,那么它们互相垂直,即.
对两直线垂直与斜率的关系要注意以下几点
(1)成立的前提条件是:①两条直线的斜率都存在;②且.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【即学即练2】(多选)(2023·广西钦州·高二浦北中学统考期末)已知两条不重合的直线,,下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】ABD
【详解】对A,若,则,故A正确;
对B,若,又两直线不重合,则,故B正确;
对C,若,则与不垂直,故C错误;
对D,若,则,故D正确.
故选:ABD.
题型01 两直线平行关系的判定
【典例1】(多选)(2023春·广西柳州·高二校考阶段练习)已知直线与为两条不重合的直线,则下列命题正确的是( )
A.若,则斜率
B.若斜率,则
C.若倾斜角,则
D.若,则倾斜角
【答案】BCD
【详解】A选项,,可能直线与的倾斜角都是,斜率不存在,所以A选项错误.
B选项,根据直线的位置关系,当直线的斜率存在,并且相等,则直线平行,所以B选项正确.
C选项,当两条直线的倾斜角相等时,直线平行,所以C选项正确.
D选项,当两条直线平行时,则倾斜角必相等,所以D选项正确.
故选:BCD
【典例2】(2023春·山东滨州·高一校考阶段练习)已知点,,,,试判定四边形的形状.
【答案】直角梯形
【详解】由斜率公式可得:
,
与BC不平行
又,
,
故四边形ABCD是直角梯形.
【典例3】(2023·江苏·高二假期作业)判断下列各组直线是否平行,并说明理由.
(1)经过点,经过点;
(2)的斜率为,经过点.
【答案】(1)不平行,理由见解析
(2)不平行,理由见解析
【详解】(1)设直线,的斜率分别为,,
因为经过点,经过点,
所以,,
所以,
所以与不平行;
(2)设直线,的斜率分别为,,则,
因为经过点,
所以,
所以,
所以与不平行.
【变式1】(2023·江苏·高二假期作业)判断下列各题中直线与是否平行.
(1)经过点,,经过点,;
(2)经过点,,经过点,.
【答案】(1)不平行
(2)平行
【详解】(1)因为经过点,,所以,
又经过点,,所以,
因为,所以与不平行;
(2)直线经过点,的方程为,
直线经过点,的方程为,
故直线和直线平行;
【变式2】(2023·全国·高二专题练习)判断下列不同的直线与是否平行.
(1)的斜率为2,经过,两点;
(2)经过,两点,平行于轴,但不经过,两点;
(3)经过,两点,经过,两点.
【答案】(1)平行;(2)平行;(3)平行.
【详解】(1)经过,两点,则,
则,可得两直线平行.
(2)经过,两点,可得平行于x轴,
平行于x轴,但不经过P,Q两点,所以;
(3)经过,两点,,
经过,两点,则,
所以.
题型02两直线垂直关系的判定
【典例1】(2023秋·高二课时练习)以为顶点的四边形是( )
A.平行四边形,但不是矩形 B.矩形 C.梯形,但不是直角梯形 D.直角梯形
【答案】D
【详解】
在坐标系中画出ABCD点,大致如上图,其中,
,
,
所以四边形ABCD是直角梯形;
故选:D.
【典例2】(2023·江苏·高二假期作业)判断下列各组直线是否垂直,并说明理由.
(1)经过点经过点;
(2)经过点经过点.
【答案】(1)不垂直,理由见解析
(2)垂直,理由见解析
【详解】(1)由题知直线,的斜率存在,分别设为,
,
,
,
∴与不垂直.
(2)由题意知的倾斜角为90°,
则轴;
由题知直线的斜率存在,设为,
,
则轴,
∴.
【变式1】(多选)(2023春·广西柳州·高二校考阶段练习)(多选)若,,,,下面结论中正确的是( )
A. B. C. D.
【答案】ABC
【详解】,,且C不在直线AB上,∴,故A正确;
又∵,∴,∴,故B正确;
∵,,
∴,,∴,故C正确;
又∵,,∴
∴,故D错误.
故选:ABC.
【变式2】(2023·江苏·高二假期作业)已知四边形的顶点坐标为,求证:四边形为矩形.
【答案】证明见解析
【详解】因为,
所以,,
所以,,
所以∥,∥,
所以四边形为平行四边形,
因为,
所以,
所以四边形为矩形.
题型03已知两直线平行关求参数
【典例1】(2023·江苏·高二假期作业)已知过和的直线与斜率为-2的直线平行,则的值是( )
A.-8 B.0 C.2 D.10
【答案】A
【详解】由题意可知,,解得.
故选:A
【典例2】(2022秋·四川遂宁·高二遂宁中学校考阶段练习)若直线与平行,则( )
A. B. C. D.
【答案】C
【详解】直线与平行,
所以,.
故选:C.
【典例3】(2022秋·河南濮阳·高二校考阶段练习)若直线与直线平行,直线的斜率为,则直线的倾斜角为___________.
【答案】
【详解】解:因为直线与直线平行,直线的斜率为,
所以直线的斜率与直线的斜率相等,即直线的斜率为,
设直线的倾斜角为,则,
所以,即直线的倾斜角为,
故答案为:.
【变式1】(2023·江苏·高二假期作业)已知直线的倾斜角为,直线的斜率为,若∥,则的值为________.
【答案】/2或/或2
【详解】由题意知,解得.
故答案为:
【变式2】(2022·高二课时练习)过点两点的直线与直线平行,直线的倾斜角为,则___________
【答案】
【详解】因为直线的倾斜角为,所以直线的斜率,
过两点的直线的斜率,
由直线与直线平行,
所以解得.
故答案为:.
题型04已知两直线垂直关求参数
【典例1】(2023·全国·高二专题练习)过点,的直线与过点,的直线垂直,则的值为( )
A. B.2 C. D.
【答案】A
【详解】两条直线垂直,则:,解得,
故选:A.
【典例2】(2023春·甘肃兰州·高二兰州五十九中校考开学考试)已知经过点和点的直线与经过点和点的直线互相垂直,则实数的值为( )
A. B. C.或 D.或
【答案】C
【详解】直线的斜率.
①当时,直线的斜率.
因为,所以,即,解得.
②当时,、,此时直线为轴,
又、,则直线为轴,显然.
综上可知,或.
故选:C.
【典例3】(2023春·黑龙江佳木斯·高二富锦市第一中学校考阶段练习)已知直线经过,两点,且直线,则直线的倾斜角为( )
A. B. C. D.
【答案】B
【详解】设直线的倾斜角为,
因为直线的斜率,由,得,
所以,即,又,则,
所以直线的倾斜角为.
故选:B.
【变式1】(2023春·甘肃武威·高二民勤县第一中学校考开学考试)已知三角形三个顶点的坐标分别为,,,则边上的高的斜率为( )
A.2 B. C. D.
【答案】C
【详解】,,
设边上的高的斜率为,则,
故选:C
【变式2】(2023秋·浙江杭州·高二浙江省杭州第二中学校考期末)已知点和,点在轴上,且为直角,则点坐标为( )
A. B.或 C.或 D.
【答案】B
【详解】由题意,设点,
为直角,,
由,
,
解得或,所以点的坐标为或
故选:B
题型05直线平行、垂直在几何中的应用
【典例1】(2022秋·青海海东·高二校考期中)已知点,,,是的垂心.则点的坐标为( )
A. B. C. D.
【答案】D
【详解】设C点标为,直线AH斜率,
∴,而点B的横坐标为6,则,
直线BH的斜率,
∴直线AC斜率,
∴,
∴点C的坐标为.
故选:.
【典例2】(2022·高二课时练习)已知点,,,,求证:四边形是梯形.
【答案】证明见解析
【详解】由点,,,,
可得 ,
而 , ,
故,但 ,
所以四边形ABCD是梯形.
【变式1】(2022·高二课时练习)顺次连接,,),)所构成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对
【答案】B
【详解】,,则,
所以,与不平行,
因此
故构成的图形为直角梯形.
故选:B.
【变式2】(2023·全国·高二专题练习)已知的三个顶点的坐标分别为,,,则顶点的坐标为________.
【答案】(3,4)
【详解】设顶点D的坐标为(x,y),
∵ABDC,ADBC,
∴,解得,
∴点D的坐标为(3,4).
故答案为:(3,4).
【变式3】(2023·江苏·高二假期作业)已知,,,四点,若顺次连接四点,试判断图形的形状.
【答案】直角梯形
【详解】由斜率公式,得,,,,
所以,又因为 ,说明与不重合,
所以.
因为,所以与不平行.
又因为,所以.
故四边形为直角梯形.
A夯实基础 B能力提升
A夯实基础
1.(2023秋·广东广州·高二广州市培正中学校考期中)已知直线的倾斜角为,直线,则直线的斜率为( )
A. B. C. D.
【答案】C
【详解】因为直线的倾斜角为,所以,
又,所以.
故选:C.
2.(2023秋·山东泰安·高二统考期末)若直线与直线平行,则实数k的值为( )
A. B. C. D.3
【答案】D
【详解】因为直线与直线平行,
所以两直线斜率相等,即.
故选:D.
3.(2023·全国·高二专题练习)下列说法中正确的是( )
A.若两条直线斜率相等,则它们互相平行
B.若,则
C.若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交
D.若两条直线的斜率都不存在,则它们相互平行
【答案】C
【详解】若两条直线斜率相等,则它们互相平行或重合,A错误;
若,则或,的斜率都不存在,B错误;
若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交,C正确;
若两条直线的斜率都不存在,则它们互相平行或重合,D错误.
故选:C.
4.(2023秋·天津和平·高二天津一中校考期末)已知直线:,:,若,则实数( )
A.-2 B.-1 C.0 D.1
【答案】D
【详解】已知直线:,:,
因为,
所以
故选:D
5.(2023春·上海长宁·高二上海市第三女子中学校考期中)“两条直线的斜率乘积为”是“两条直线互相垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
【答案】A
【详解】当两条直线斜率乘积为时,两条直线互相垂直,充分性成立;
当两条直线互相垂直时,其中一条直线可能斜率不存在,必要性不成立;
“两条直线的斜率乘积为”是“两条直线互相垂直”的充分不必要条件.
故选:A.
6.(2023春·河北承德·高二承德市双滦区实验中学校考开学考试)已知直线经过,两点,直线的倾斜角为,那么与
A.垂直 B.平行 C.重合 D.相交但不垂直
【答案】A
【详解】直线经过,两点 直线的斜率:
直线的倾斜角为 直线的斜率:
本题正确选项:
二、多选题
7.(2022秋·高二课时练习)下列说法中正确的有( )
A.若两直线平行,则两直线的斜率相等
B.若两直线的斜率相等,则两直线平行
C.若两直线的斜率乘积等于,则两直线垂直
D.若两直线垂直,则两直线的斜率乘积等于
【答案】BC
【详解】对于A,两直线平行,可以是斜率都不存在,所以A错误;
对于B,若两直线的斜率相等,则两直线平行,所以B正确;
对于C,若两直线的斜率乘积等于,则两直线垂直,故C正确;
对于D,若两直线垂直,可能是一条直线斜率为0,另一条直线斜率不存在,则不是两直线的斜率乘积等于,故D错误;
故选:BC
8.(2022秋·新疆喀什·高二新疆维吾尔自治区喀什第六中学校考期中)若与为两条不重合的直线,则下列说法中正确的有( )
A.若,则它们的斜率相等 B.若与的斜率相等,则
C.若,则它们的倾斜角相等 D.若与的倾斜角相等,则
【答案】BCD
【详解】对于A,当和倾斜角均为时,,但两直线斜率不存在,A错误;
对于B,若和斜率相等,则两直线倾斜角相等,可知,B正确;
对于C,若,可知两直线倾斜角相等,C正确;
对于D,若两直线倾斜角相等,则两直线斜率相等或两直线斜率均不存在,可知,D正确.
故选:BCD.
三、填空题
9.(2022秋·广西玉林·高二校考阶段练习)若与为两条不重合的直线,它们的倾斜角分别为,,斜率分别为,,则下列命题
①若,则斜率; ②若斜率,则;
③若,则倾斜角;④若倾斜角,则;
其中正确命题的个数是______.
【答案】
【详解】解:因为与为两条不重合的直线,且它们的倾斜角分别为,,斜率分别为,.
①由于斜率都存在,若,则,此命题正确;
②因为两直线的斜率相等即斜率,得到倾斜角的正切值相等即,即可得到,所以,此命题正确;
由于与互相垂直,
所以,即,
所以.
12.(2022·全国·高二专题练习)判断三点是否共线,并说明理由.
【答案】共线,理由见解析.
【详解】这三点共线,理由如下:
由直线斜率公式可得:,
直线的斜率相同,所以这两直线平行,但这两直线都通过同一点,
所以这三点共线.
B能力提升
13.(2021春·高一课时练习)根据下列给定的条件,判断直线与直线是否平行.
(1)直线经过点,直线经过点;
(2)直线平行于y轴,直线经过点,;
(3)直线经过点,直线经过点.
【答案】(1)不平行;(2)平行;(3)不平行.
【详解】解:(1)直线的斜率,直线的斜率,显然,所以直线与不平行.
(2)直线与y轴重合,所以直线与平行.
(3)直线的斜率,直线的斜率,所以,又,所以E,F,G,H四点共线,直线与重合.故直线与不平行.
21世纪教育网(www.21cnjy.com)
课程标准 学习目标
①理解两条直线平行的条件及两条直线 垂直的条件。 ②能根据直线的斜率判断两条直线平行或垂直.。 ③能应用两条直线平行或垂直解决相关问题,理解用代数法解决几何问题.。 通过本节课的学习,理解两条直线平行与垂直的几何位置与代数运算相结合的条件与意义,能应用两直线的斜率的关系判断两直线的位置关系,并能解决与两条直线位置关系相关联的综合问题.
知识点01:两条直线平行
对于两条不重合的直线,,其斜率分别为,,有.
对两直线平行与斜率的关系要注意以下几点
(1)成立的前提条件是:
①两条直线的斜率都存在;
②与不重合.
(2)当两条直线不重合且斜率都不存在时,与的倾斜角都是,则.
(3)两条不重合直线平行的判定的一般结论是:
或,斜率都不存在.
【即学即练1】(多选)(2023·广西桂林·高二校考期中)若为两条不重合的直线,他们的倾斜角分别为,斜率分别为,则下列命题正确的是( )
A.若,则斜率 B.若斜率,则
C.若,则倾斜角 D.若倾斜角,则
【答案】ABCD
【详解】因为为两条不重合的直线,他们的倾斜角分别为,斜率分别为,
若,则斜率相等,即;又斜率是倾斜角的正切值,所以,故AC正确;
若,则,所以,故BD正确;
故选:ABCD
知识点02:两条直线垂直
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果它们的斜率之积等于,那么它们互相垂直,即.
对两直线垂直与斜率的关系要注意以下几点
(1)成立的前提条件是:①两条直线的斜率都存在;②且.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【即学即练2】(多选)(2023·广西钦州·高二浦北中学统考期末)已知两条不重合的直线,,下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】ABD
【详解】对A,若,则,故A正确;
对B,若,又两直线不重合,则,故B正确;
对C,若,则与不垂直,故C错误;
对D,若,则,故D正确.
故选:ABD.
题型01 两直线平行关系的判定
【典例1】(多选)(2023春·广西柳州·高二校考阶段练习)已知直线与为两条不重合的直线,则下列命题正确的是( )
A.若,则斜率
B.若斜率,则
C.若倾斜角,则
D.若,则倾斜角
【典例2】(2023春·山东滨州·高一校考阶段练习)已知点,,,,试判定四边形的形状.
【典例3】(2023·江苏·高二假期作业)判断下列各组直线是否平行,并说明理由.
(1)经过点,经过点;
(2)的斜率为,经过点.
【变式1】(2023·江苏·高二假期作业)判断下列各题中直线与是否平行.
(1)经过点,,经过点,;
(2)经过点,,经过点,.
【变式2】(2023·全国·高二专题练习)判断下列不同的直线与是否平行.
(1)的斜率为2,经过,两点;
(2)经过,两点,平行于轴,但不经过,两点;
(3)经过,两点,经过,两点.
题型02两直线垂直关系的判定
【典例1】(2023秋·高二课时练习)以为顶点的四边形是( )
A.平行四边形,但不是矩形 B.矩形 C.梯形,但不是直角梯形 D.直角梯形
【典例2】(2023·江苏·高二假期作业)判断下列各组直线是否垂直,并说明理由.
(1)经过点经过点;
(2)经过点经过点.
【变式1】(多选)(2023春·广西柳州·高二校考阶段练习)(多选)若,,,,下面结论中正确的是( )
A. B. C. D.
【变式2】(2023·江苏·高二假期作业)已知四边形的顶点坐标为,求证:四边形为矩形.
题型03已知两直线平行关求参数
【典例1】(2023·江苏·高二假期作业)已知过和的直线与斜率为-2的直线平行,则的值是( )
A.-8 B.0 C.2 D.10
【典例2】(2022秋·四川遂宁·高二遂宁中学校考阶段练习)若直线与平行,则( )
A. B. C. D.
【典例3】(2022秋·河南濮阳·高二校考阶段练习)若直线与直线平行,直线的斜率为,则直线的倾斜角为___________.
【变式1】(2023·江苏·高二假期作业)已知直线的倾斜角为,直线的斜率为,若∥,则的值为________.
【变式2】(2022·高二课时练习)过点两点的直线与直线平行,直线的倾斜角为,则___________
题型04已知两直线垂直关求参数
【典例1】(2023·全国·高二专题练习)过点,的直线与过点,的直线垂直,则的值为( )
A. B.2 C. D.
【典例2】(2023春·甘肃兰州·高二兰州五十九中校考开学考试)已知经过点和点的直线与经过点和点的直线互相垂直,则实数的值为( )
A. B. C.或 D.或
【典例3】(2023春·黑龙江佳木斯·高二富锦市第一中学校考阶段练习)已知直线经过,两点,且直线,则直线的倾斜角为( )
A. B. C. D.
【变式1】(2023春·甘肃武威·高二民勤县第一中学校考开学考试)已知三角形三个顶点的坐标分别为,,,则边上的高的斜率为( )
A.2 B. C. D.
【变式2】(2023秋·浙江杭州·高二浙江省杭州第二中学校考期末)已知点和,点在轴上,且为直角,则点坐标为( )
A. B.或 C.或 D.
题型05直线平行、垂直在几何中的应用
【典例1】(2022秋·青海海东·高二校考期中)已知点,,,是的垂心.则点的坐标为( )
A. B. C. D.
【典例2】(2022·高二课时练习)已知点,,,,求证:四边形是梯形.
【变式1】(2022·高二课时练习)顺次连接,,),)所构成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对
【变式2】(2023·全国·高二专题练习)已知的三个顶点的坐标分别为,,,则顶点的坐标为________.
【变式3】(2023·江苏·高二假期作业)已知,,,四点,若顺次连接四点,试判断图形的形状.
A夯实基础 B能力提升
A夯实基础
1.(2023秋·广东广州·高二广州市培正中学校考期中)已知直线的倾斜角为,直线,则直线的斜率为( )
A. B. C. D.
2.(2023秋·山东泰安·高二统考期末)若直线与直线平行,则实数k的值为( )
A. B. C. D.3
3.(2023·全国·高二专题练习)下列说法中正确的是( )
A.若两条直线斜率相等,则它们互相平行
B.若,则
C.若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交
D.若两条直线的斜率都不存在,则它们相互平行
4.(2023秋·天津和平·高二天津一中校考期末)已知直线:,:,若,则实数( )
A.-2 B.-1 C.0 D.1
5.(2023春·上海长宁·高二上海市第三女子中学校考期中)“两条直线的斜率乘积为”是“两条直线互相垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
12.(2022·全国·高二专题练习)判断三点是否共线,并说明理由.
B能力提升
13.(2021春·高一课时练习)根据下列给定的条件,判断直线与直线是否平行.
(1)直线经过点,直线经过点;
(2)直线平行于y轴,直线经过点,;
(3)直线经过点,直线经过点.
第02讲 2.1.2两条直线平行和垂直的判定
课程标准 学习目标
①理解两条直线平行的条件及两条直线 垂直的条件。 ②能根据直线的斜率判断两条直线平行或垂直.。 ③能应用两条直线平行或垂直解决相关问题,理解用代数法解决几何问题.。 通过本节课的学习,理解两条直线平行与垂直的几何位置与代数运算相结合的条件与意义,能应用两直线的斜率的关系判断两直线的位置关系,并能解决与两条直线位置关系相关联的综合问题.
知识点01:两条直线平行
对于两条不重合的直线,,其斜率分别为,,有.
对两直线平行与斜率的关系要注意以下几点
(1)成立的前提条件是:
①两条直线的斜率都存在;
②与不重合.
(2)当两条直线不重合且斜率都不存在时,与的倾斜角都是,则.
(3)两条不重合直线平行的判定的一般结论是:
或,斜率都不存在.
【即学即练1】(多选)(2023·广西桂林·高二校考期中)若为两条不重合的直线,他们的倾斜角分别为,斜率分别为,则下列命题正确的是( )
A.若,则斜率 B.若斜率,则
C.若,则倾斜角 D.若倾斜角,则
【答案】ABCD
【详解】因为为两条不重合的直线,他们的倾斜角分别为,斜率分别为,
若,则斜率相等,即;又斜率是倾斜角的正切值,所以,故AC正确;
若,则,所以,故BD正确;
故选:ABCD
知识点02:两条直线垂直
如果两条直线都有斜率,且它们互相垂直,那么它们的斜率之积等于;反之,如果它们的斜率之积等于,那么它们互相垂直,即.
对两直线垂直与斜率的关系要注意以下几点
(1)成立的前提条件是:①两条直线的斜率都存在;②且.
(2)两条直线中,一条直线的斜率不存在,同时另一条直线的斜率等于零,则两条直线垂直.
(3)判定两条直线垂直的一般结论为:
或一条直线的斜率不存在,同时另一条直线的斜率等于零.
【即学即练2】(多选)(2023·广西钦州·高二浦北中学统考期末)已知两条不重合的直线,,下列结论正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
【答案】ABD
【详解】对A,若,则,故A正确;
对B,若,又两直线不重合,则,故B正确;
对C,若,则与不垂直,故C错误;
对D,若,则,故D正确.
故选:ABD.
题型01 两直线平行关系的判定
【典例1】(多选)(2023春·广西柳州·高二校考阶段练习)已知直线与为两条不重合的直线,则下列命题正确的是( )
A.若,则斜率
B.若斜率,则
C.若倾斜角,则
D.若,则倾斜角
【答案】BCD
【详解】A选项,,可能直线与的倾斜角都是,斜率不存在,所以A选项错误.
B选项,根据直线的位置关系,当直线的斜率存在,并且相等,则直线平行,所以B选项正确.
C选项,当两条直线的倾斜角相等时,直线平行,所以C选项正确.
D选项,当两条直线平行时,则倾斜角必相等,所以D选项正确.
故选:BCD
【典例2】(2023春·山东滨州·高一校考阶段练习)已知点,,,,试判定四边形的形状.
【答案】直角梯形
【详解】由斜率公式可得:
,
与BC不平行
又,
,
故四边形ABCD是直角梯形.
【典例3】(2023·江苏·高二假期作业)判断下列各组直线是否平行,并说明理由.
(1)经过点,经过点;
(2)的斜率为,经过点.
【答案】(1)不平行,理由见解析
(2)不平行,理由见解析
【详解】(1)设直线,的斜率分别为,,
因为经过点,经过点,
所以,,
所以,
所以与不平行;
(2)设直线,的斜率分别为,,则,
因为经过点,
所以,
所以,
所以与不平行.
【变式1】(2023·江苏·高二假期作业)判断下列各题中直线与是否平行.
(1)经过点,,经过点,;
(2)经过点,,经过点,.
【答案】(1)不平行
(2)平行
【详解】(1)因为经过点,,所以,
又经过点,,所以,
因为,所以与不平行;
(2)直线经过点,的方程为,
直线经过点,的方程为,
故直线和直线平行;
【变式2】(2023·全国·高二专题练习)判断下列不同的直线与是否平行.
(1)的斜率为2,经过,两点;
(2)经过,两点,平行于轴,但不经过,两点;
(3)经过,两点,经过,两点.
【答案】(1)平行;(2)平行;(3)平行.
【详解】(1)经过,两点,则,
则,可得两直线平行.
(2)经过,两点,可得平行于x轴,
平行于x轴,但不经过P,Q两点,所以;
(3)经过,两点,,
经过,两点,则,
所以.
题型02两直线垂直关系的判定
【典例1】(2023秋·高二课时练习)以为顶点的四边形是( )
A.平行四边形,但不是矩形 B.矩形 C.梯形,但不是直角梯形 D.直角梯形
【答案】D
【详解】
在坐标系中画出ABCD点,大致如上图,其中,
,
,
所以四边形ABCD是直角梯形;
故选:D.
【典例2】(2023·江苏·高二假期作业)判断下列各组直线是否垂直,并说明理由.
(1)经过点经过点;
(2)经过点经过点.
【答案】(1)不垂直,理由见解析
(2)垂直,理由见解析
【详解】(1)由题知直线,的斜率存在,分别设为,
,
,
,
∴与不垂直.
(2)由题意知的倾斜角为90°,
则轴;
由题知直线的斜率存在,设为,
,
则轴,
∴.
【变式1】(多选)(2023春·广西柳州·高二校考阶段练习)(多选)若,,,,下面结论中正确的是( )
A. B. C. D.
【答案】ABC
【详解】,,且C不在直线AB上,∴,故A正确;
又∵,∴,∴,故B正确;
∵,,
∴,,∴,故C正确;
又∵,,∴
∴,故D错误.
故选:ABC.
【变式2】(2023·江苏·高二假期作业)已知四边形的顶点坐标为,求证:四边形为矩形.
【答案】证明见解析
【详解】因为,
所以,,
所以,,
所以∥,∥,
所以四边形为平行四边形,
因为,
所以,
所以四边形为矩形.
题型03已知两直线平行关求参数
【典例1】(2023·江苏·高二假期作业)已知过和的直线与斜率为-2的直线平行,则的值是( )
A.-8 B.0 C.2 D.10
【答案】A
【详解】由题意可知,,解得.
故选:A
【典例2】(2022秋·四川遂宁·高二遂宁中学校考阶段练习)若直线与平行,则( )
A. B. C. D.
【答案】C
【详解】直线与平行,
所以,.
故选:C.
【典例3】(2022秋·河南濮阳·高二校考阶段练习)若直线与直线平行,直线的斜率为,则直线的倾斜角为___________.
【答案】
【详解】解:因为直线与直线平行,直线的斜率为,
所以直线的斜率与直线的斜率相等,即直线的斜率为,
设直线的倾斜角为,则,
所以,即直线的倾斜角为,
故答案为:.
【变式1】(2023·江苏·高二假期作业)已知直线的倾斜角为,直线的斜率为,若∥,则的值为________.
【答案】/2或/或2
【详解】由题意知,解得.
故答案为:
【变式2】(2022·高二课时练习)过点两点的直线与直线平行,直线的倾斜角为,则___________
【答案】
【详解】因为直线的倾斜角为,所以直线的斜率,
过两点的直线的斜率,
由直线与直线平行,
所以解得.
故答案为:.
题型04已知两直线垂直关求参数
【典例1】(2023·全国·高二专题练习)过点,的直线与过点,的直线垂直,则的值为( )
A. B.2 C. D.
【答案】A
【详解】两条直线垂直,则:,解得,
故选:A.
【典例2】(2023春·甘肃兰州·高二兰州五十九中校考开学考试)已知经过点和点的直线与经过点和点的直线互相垂直,则实数的值为( )
A. B. C.或 D.或
【答案】C
【详解】直线的斜率.
①当时,直线的斜率.
因为,所以,即,解得.
②当时,、,此时直线为轴,
又、,则直线为轴,显然.
综上可知,或.
故选:C.
【典例3】(2023春·黑龙江佳木斯·高二富锦市第一中学校考阶段练习)已知直线经过,两点,且直线,则直线的倾斜角为( )
A. B. C. D.
【答案】B
【详解】设直线的倾斜角为,
因为直线的斜率,由,得,
所以,即,又,则,
所以直线的倾斜角为.
故选:B.
【变式1】(2023春·甘肃武威·高二民勤县第一中学校考开学考试)已知三角形三个顶点的坐标分别为,,,则边上的高的斜率为( )
A.2 B. C. D.
【答案】C
【详解】,,
设边上的高的斜率为,则,
故选:C
【变式2】(2023秋·浙江杭州·高二浙江省杭州第二中学校考期末)已知点和,点在轴上,且为直角,则点坐标为( )
A. B.或 C.或 D.
【答案】B
【详解】由题意,设点,
为直角,,
由,
,
解得或,所以点的坐标为或
故选:B
题型05直线平行、垂直在几何中的应用
【典例1】(2022秋·青海海东·高二校考期中)已知点,,,是的垂心.则点的坐标为( )
A. B. C. D.
【答案】D
【详解】设C点标为,直线AH斜率,
∴,而点B的横坐标为6,则,
直线BH的斜率,
∴直线AC斜率,
∴,
∴点C的坐标为.
故选:.
【典例2】(2022·高二课时练习)已知点,,,,求证:四边形是梯形.
【答案】证明见解析
【详解】由点,,,,
可得 ,
而 , ,
故,但 ,
所以四边形ABCD是梯形.
【变式1】(2022·高二课时练习)顺次连接,,),)所构成的图形是( )
A.平行四边形 B.直角梯形
C.等腰梯形 D.以上都不对
【答案】B
【详解】,,则,
所以,与不平行,
因此
故构成的图形为直角梯形.
故选:B.
【变式2】(2023·全国·高二专题练习)已知的三个顶点的坐标分别为,,,则顶点的坐标为________.
【答案】(3,4)
【详解】设顶点D的坐标为(x,y),
∵ABDC,ADBC,
∴,解得,
∴点D的坐标为(3,4).
故答案为:(3,4).
【变式3】(2023·江苏·高二假期作业)已知,,,四点,若顺次连接四点,试判断图形的形状.
【答案】直角梯形
【详解】由斜率公式,得,,,,
所以,又因为 ,说明与不重合,
所以.
因为,所以与不平行.
又因为,所以.
故四边形为直角梯形.
A夯实基础 B能力提升
A夯实基础
1.(2023秋·广东广州·高二广州市培正中学校考期中)已知直线的倾斜角为,直线,则直线的斜率为( )
A. B. C. D.
【答案】C
【详解】因为直线的倾斜角为,所以,
又,所以.
故选:C.
2.(2023秋·山东泰安·高二统考期末)若直线与直线平行,则实数k的值为( )
A. B. C. D.3
【答案】D
【详解】因为直线与直线平行,
所以两直线斜率相等,即.
故选:D.
3.(2023·全国·高二专题练习)下列说法中正确的是( )
A.若两条直线斜率相等,则它们互相平行
B.若,则
C.若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交
D.若两条直线的斜率都不存在,则它们相互平行
【答案】C
【详解】若两条直线斜率相等,则它们互相平行或重合,A错误;
若,则或,的斜率都不存在,B错误;
若两条直线中有一条直线的斜率不存在,另一条直线的斜率存在,则这两条直线相交,C正确;
若两条直线的斜率都不存在,则它们互相平行或重合,D错误.
故选:C.
4.(2023秋·天津和平·高二天津一中校考期末)已知直线:,:,若,则实数( )
A.-2 B.-1 C.0 D.1
【答案】D
【详解】已知直线:,:,
因为,
所以
故选:D
5.(2023春·上海长宁·高二上海市第三女子中学校考期中)“两条直线的斜率乘积为”是“两条直线互相垂直”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
【答案】A
【详解】当两条直线斜率乘积为时,两条直线互相垂直,充分性成立;
当两条直线互相垂直时,其中一条直线可能斜率不存在,必要性不成立;
“两条直线的斜率乘积为”是“两条直线互相垂直”的充分不必要条件.
故选:A.
6.(2023春·河北承德·高二承德市双滦区实验中学校考开学考试)已知直线经过,两点,直线的倾斜角为,那么与
A.垂直 B.平行 C.重合 D.相交但不垂直
【答案】A
【详解】直线经过,两点 直线的斜率:
直线的倾斜角为 直线的斜率:
本题正确选项:
二、多选题
7.(2022秋·高二课时练习)下列说法中正确的有( )
A.若两直线平行,则两直线的斜率相等
B.若两直线的斜率相等,则两直线平行
C.若两直线的斜率乘积等于,则两直线垂直
D.若两直线垂直,则两直线的斜率乘积等于
【答案】BC
【详解】对于A,两直线平行,可以是斜率都不存在,所以A错误;
对于B,若两直线的斜率相等,则两直线平行,所以B正确;
对于C,若两直线的斜率乘积等于,则两直线垂直,故C正确;
对于D,若两直线垂直,可能是一条直线斜率为0,另一条直线斜率不存在,则不是两直线的斜率乘积等于,故D错误;
故选:BC
8.(2022秋·新疆喀什·高二新疆维吾尔自治区喀什第六中学校考期中)若与为两条不重合的直线,则下列说法中正确的有( )
A.若,则它们的斜率相等 B.若与的斜率相等,则
C.若,则它们的倾斜角相等 D.若与的倾斜角相等,则
【答案】BCD
【详解】对于A,当和倾斜角均为时,,但两直线斜率不存在,A错误;
对于B,若和斜率相等,则两直线倾斜角相等,可知,B正确;
对于C,若,可知两直线倾斜角相等,C正确;
对于D,若两直线倾斜角相等,则两直线斜率相等或两直线斜率均不存在,可知,D正确.
故选:BCD.
三、填空题
9.(2022秋·广西玉林·高二校考阶段练习)若与为两条不重合的直线,它们的倾斜角分别为,,斜率分别为,,则下列命题
①若,则斜率; ②若斜率,则;
③若,则倾斜角;④若倾斜角,则;
其中正确命题的个数是______.
【答案】
【详解】解:因为与为两条不重合的直线,且它们的倾斜角分别为,,斜率分别为,.
①由于斜率都存在,若,则,此命题正确;
②因为两直线的斜率相等即斜率,得到倾斜角的正切值相等即,即可得到,所以,此命题正确;
由于与互相垂直,
所以,即,
所以.
12.(2022·全国·高二专题练习)判断三点是否共线,并说明理由.
【答案】共线,理由见解析.
【详解】这三点共线,理由如下:
由直线斜率公式可得:,
直线的斜率相同,所以这两直线平行,但这两直线都通过同一点,
所以这三点共线.
B能力提升
13.(2021春·高一课时练习)根据下列给定的条件,判断直线与直线是否平行.
(1)直线经过点,直线经过点;
(2)直线平行于y轴,直线经过点,;
(3)直线经过点,直线经过点.
【答案】(1)不平行;(2)平行;(3)不平行.
【详解】解:(1)直线的斜率,直线的斜率,显然,所以直线与不平行.
(2)直线与y轴重合,所以直线与平行.
(3)直线的斜率,直线的斜率,所以,又,所以E,F,G,H四点共线,直线与重合.故直线与不平行.
21世纪教育网(www.21cnjy.com)
