23.2.2 中心对称图形 课时巩固练 2024--2025学年上学期初中数学人教版九年级上册
文档属性
| 名称 | 23.2.2 中心对称图形 课时巩固练 2024--2025学年上学期初中数学人教版九年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 611.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 14:53:49 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
23.2.2 中心对称图形 课时巩固练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.如图,已知图形是中心对称图形,则对称中心是( )
A.点 B.点
C.线段的中点 D.线段的中点
3.如图,在的方格中,有3个被涂黑的小正方形.若在其余空白的小正方形中选择1个涂黑,使涂黑的小正方形组成的新图形是中心对称图形,则可选择的小正方形有( )
A.1个 B.2个 C.3个 D.5个
4.如图,老师让同学们利用棋子在棋盘上拼出一个中心对称图形(颜色忽略),为了增加难度,加入了方向角,则下一个棋子应该放在中心点的( )
A.西北方向的处 B.西南方向的处
C.东南方向的处 D.西南方向的处
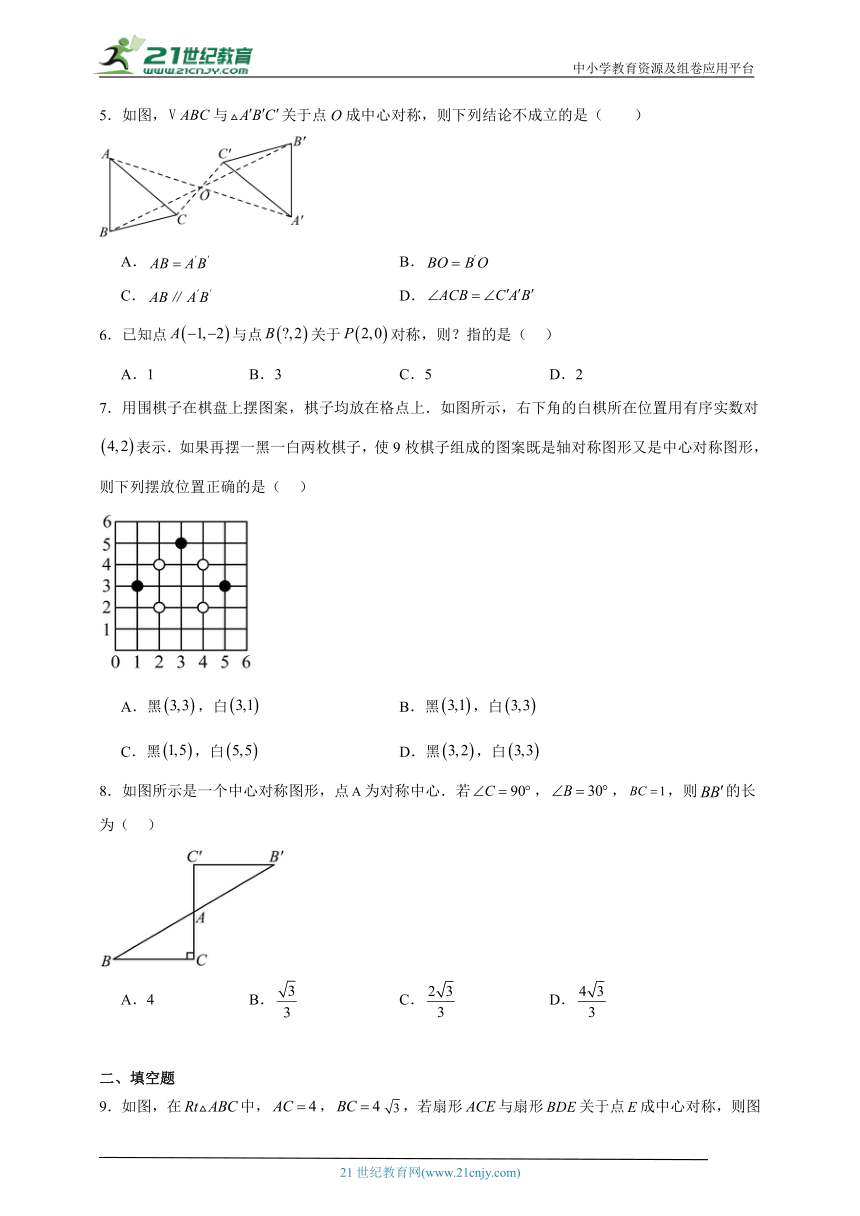
5.如图,与关于点O成中心对称,则下列结论不成立的是( )
A. B.
C. D.
6.已知点与点关于对称,则?指的是( )
A.1 B.3 C.5 D.2
7.用围棋子在棋盘上摆图案,棋子均放在格点上.如图所示,右下角的白棋所在位置用有序实数对表示.如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放位置正确的是( )
A.黑,白 B.黑,白
C.黑,白 D.黑,白
8.如图所示是一个中心对称图形,点为对称中心.若,,,则的长为( )
A.4 B. C. D.
二、填空题
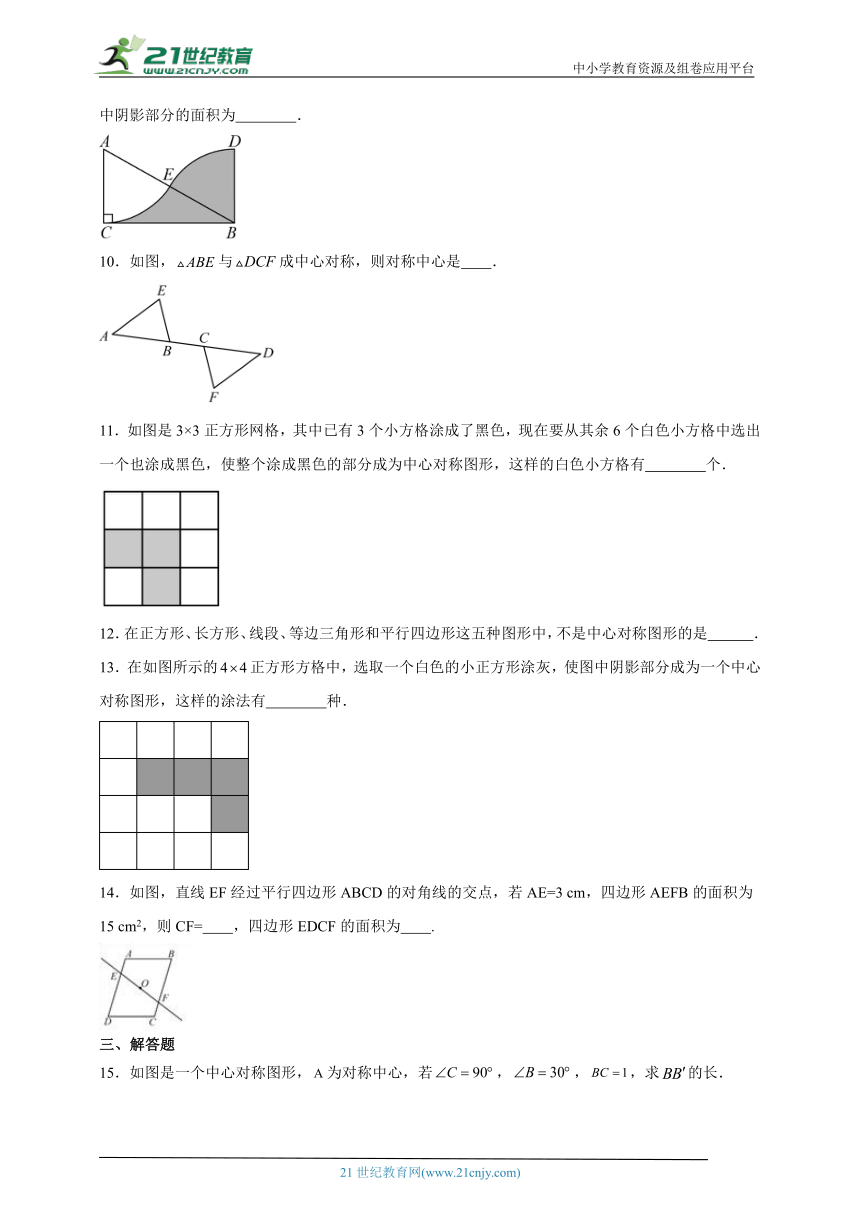
9.如图,在中,,,若扇形与扇形关于点成中心对称,则图中阴影部分的面积为 .
10.如图,与成中心对称,则对称中心是 .
11.如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色,使整个涂成黑色的部分成为中心对称图形,这样的白色小方格有 个.
12.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,不是中心对称图形的是 .
13.在如图所示的正方形方格中,选取一个白色的小正方形涂灰,使图中阴影部分成为一个中心对称图形,这样的涂法有 种.
14.如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3 cm,四边形AEFB的面积为15 cm2,则CF= ,四边形EDCF的面积为 .
三、解答题
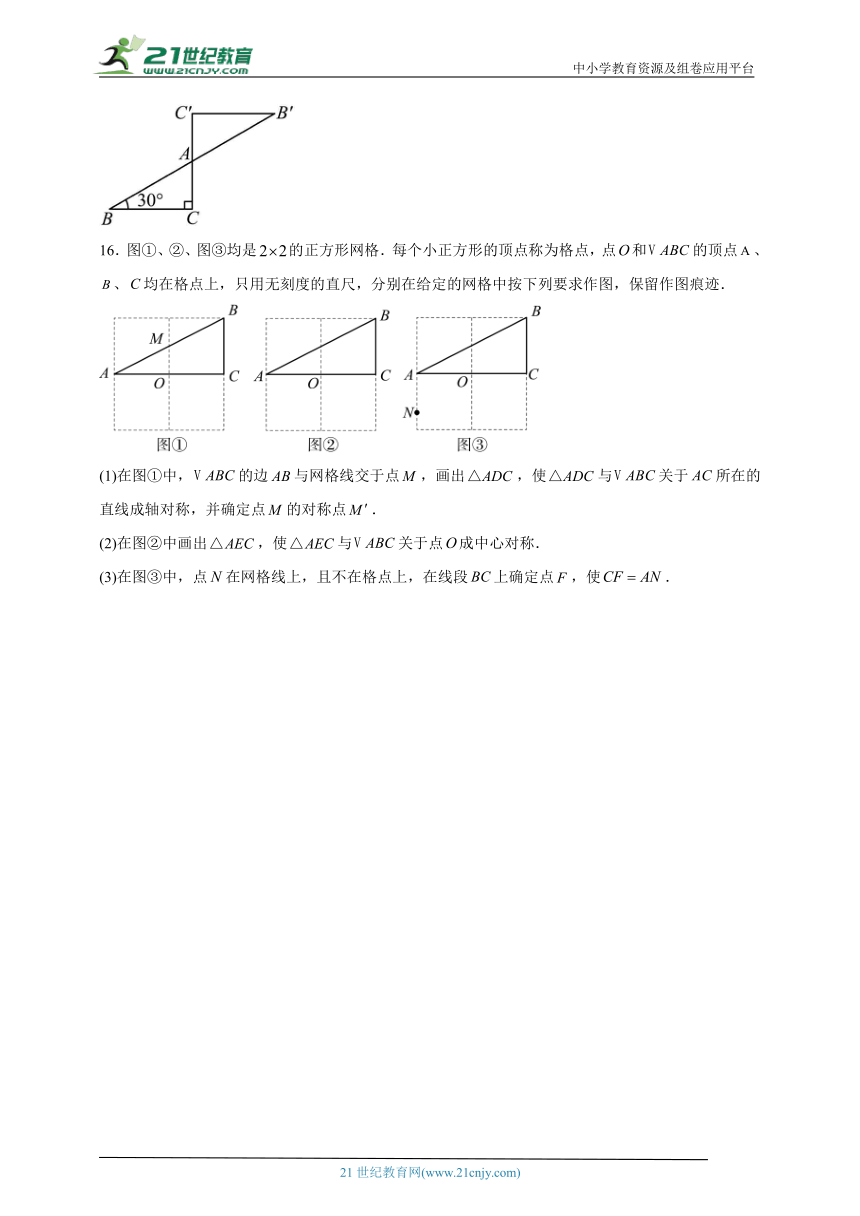
15.如图是一个中心对称图形,为对称中心,若,,,求的长.
16.图①、②、图③均是的正方形网格.每个小正方形的顶点称为格点,点和的顶点、、均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
(1)在图①中,的边与网格线交于点,画出,使与关于所在的直线成轴对称,并确定点的对称点.
(2)在图②中画出,使与关于点成中心对称.
(3)在图③中,点在网格线上,且不在格点上,在线段上确定点,使.
参考答案:
1.B
解:A、不是中心对称图形,故此选不项符合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不符合题意;
D、不是中心对称图形,故此选项不符合题意;
2.D
解:∵此图形是中心对称图形,
∴对称中心是线段的中点.
3.B
解:选择一个正方形涂黑,使得4个涂黑的正方形组成轴对称图形,如图,
共有2个,
4.D
解:A、B、C均无法找到一个点,使其绕着某个点旋转能与原来的图形重合,
D能找到一个点,使其绕着某个点旋转能与原来的图形重合,此时红点即对称点:
5.D
解:与关于点O成中心对称,
,,,故A,B,C选项正确,,故D选项错误.
6.C
解:∵点与点关于对称,
∴,
解得:,
7.B
A.当摆放黑,白时,此时图案是轴对称图形,不是中心对称图形,故A项错误;
B. 当摆放黑,白时,此时图案是轴对称图形又是中心对称图形,故B项正确;
C.当摆放黑,白时,此时图案既不是轴对称图形也不是中心对称图形,故C项错误
D.当摆放黑,白时,此时图案是轴对称图形,不是中心对称图形,故D项错误
8.D
根据中心对称图形的特点可知:,
∵,,
∴在中,,
∵在中,,,
∴,
解得:(负值舍去),
∴,
∴,
9.
解:∵扇形与扇形关于点中心对称,
∴扇形的面积与扇形的面积相等,
∴,
故答案为:.
10.中点(或中点)
解:∵与成中心对称,
∴的中点为对称中心,(的中点为对称中心)
故答案为:中点(或中点).
11.3
如图所示,
∴这样的白色小方格有3个.
故答案为:3.
12.等边三角形
解:正方形、长方形、线段、等边三角形和平行四边形这五种图形中、线段和平行四边形和正方形和长方形都是中心对称图形,只有等边三角形是旋转对称图形但不是中心对称图形;
故答案为:等边三角形.
13.1
解:根据中心对称图形的定义,可得如下涂法,且只有一种,
故答案为:1.
14. 3 15
解:连接AC,BD,
∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF=3cm.
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=15cm2.
故答案为3cm,15cm2.
15.
∵,,
∴,
设,,
在中,,
∴,
解得:(负值舍去),
∴,
∵原图形为中心对称图形,为对称中心,
∴.
16.(1)见详解
(2)见详解
(3)见详解
(1)解:如图,和点即为所求.
(2)解:如图,即为所求.
(3)解:如图,连接并延长,交于点,则点即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
23.2.2 中心对称图形 课时巩固练
2024--2025学年上学期初中数学人教版九年级上册
一、单选题
1.下列图形中,是中心对称图形的是( )
A. B. C. D.
2.如图,已知图形是中心对称图形,则对称中心是( )
A.点 B.点
C.线段的中点 D.线段的中点
3.如图,在的方格中,有3个被涂黑的小正方形.若在其余空白的小正方形中选择1个涂黑,使涂黑的小正方形组成的新图形是中心对称图形,则可选择的小正方形有( )
A.1个 B.2个 C.3个 D.5个
4.如图,老师让同学们利用棋子在棋盘上拼出一个中心对称图形(颜色忽略),为了增加难度,加入了方向角,则下一个棋子应该放在中心点的( )
A.西北方向的处 B.西南方向的处
C.东南方向的处 D.西南方向的处
5.如图,与关于点O成中心对称,则下列结论不成立的是( )
A. B.
C. D.
6.已知点与点关于对称,则?指的是( )
A.1 B.3 C.5 D.2
7.用围棋子在棋盘上摆图案,棋子均放在格点上.如图所示,右下角的白棋所在位置用有序实数对表示.如果再摆一黑一白两枚棋子,使9枚棋子组成的图案既是轴对称图形又是中心对称图形,则下列摆放位置正确的是( )
A.黑,白 B.黑,白
C.黑,白 D.黑,白
8.如图所示是一个中心对称图形,点为对称中心.若,,,则的长为( )
A.4 B. C. D.
二、填空题
9.如图,在中,,,若扇形与扇形关于点成中心对称,则图中阴影部分的面积为 .
10.如图,与成中心对称,则对称中心是 .
11.如图是3×3正方形网格,其中已有3个小方格涂成了黑色,现在要从其余6个白色小方格中选出一个也涂成黑色,使整个涂成黑色的部分成为中心对称图形,这样的白色小方格有 个.
12.在正方形、长方形、线段、等边三角形和平行四边形这五种图形中,不是中心对称图形的是 .
13.在如图所示的正方形方格中,选取一个白色的小正方形涂灰,使图中阴影部分成为一个中心对称图形,这样的涂法有 种.
14.如图,直线EF经过平行四边形ABCD的对角线的交点,若AE=3 cm,四边形AEFB的面积为15 cm2,则CF= ,四边形EDCF的面积为 .
三、解答题
15.如图是一个中心对称图形,为对称中心,若,,,求的长.
16.图①、②、图③均是的正方形网格.每个小正方形的顶点称为格点,点和的顶点、、均在格点上,只用无刻度的直尺,分别在给定的网格中按下列要求作图,保留作图痕迹.
(1)在图①中,的边与网格线交于点,画出,使与关于所在的直线成轴对称,并确定点的对称点.
(2)在图②中画出,使与关于点成中心对称.
(3)在图③中,点在网格线上,且不在格点上,在线段上确定点,使.
参考答案:
1.B
解:A、不是中心对称图形,故此选不项符合题意;
B、是中心对称图形,故此选项符合题意;
C、不是中心对称图形,故此选项不符合题意;
D、不是中心对称图形,故此选项不符合题意;
2.D
解:∵此图形是中心对称图形,
∴对称中心是线段的中点.
3.B
解:选择一个正方形涂黑,使得4个涂黑的正方形组成轴对称图形,如图,
共有2个,
4.D
解:A、B、C均无法找到一个点,使其绕着某个点旋转能与原来的图形重合,
D能找到一个点,使其绕着某个点旋转能与原来的图形重合,此时红点即对称点:
5.D
解:与关于点O成中心对称,
,,,故A,B,C选项正确,,故D选项错误.
6.C
解:∵点与点关于对称,
∴,
解得:,
7.B
A.当摆放黑,白时,此时图案是轴对称图形,不是中心对称图形,故A项错误;
B. 当摆放黑,白时,此时图案是轴对称图形又是中心对称图形,故B项正确;
C.当摆放黑,白时,此时图案既不是轴对称图形也不是中心对称图形,故C项错误
D.当摆放黑,白时,此时图案是轴对称图形,不是中心对称图形,故D项错误
8.D
根据中心对称图形的特点可知:,
∵,,
∴在中,,
∵在中,,,
∴,
解得:(负值舍去),
∴,
∴,
9.
解:∵扇形与扇形关于点中心对称,
∴扇形的面积与扇形的面积相等,
∴,
故答案为:.
10.中点(或中点)
解:∵与成中心对称,
∴的中点为对称中心,(的中点为对称中心)
故答案为:中点(或中点).
11.3
如图所示,
∴这样的白色小方格有3个.
故答案为:3.
12.等边三角形
解:正方形、长方形、线段、等边三角形和平行四边形这五种图形中、线段和平行四边形和正方形和长方形都是中心对称图形,只有等边三角形是旋转对称图形但不是中心对称图形;
故答案为:等边三角形.
13.1
解:根据中心对称图形的定义,可得如下涂法,且只有一种,
故答案为:1.
14. 3 15
解:连接AC,BD,
∵四边形ABCD是平行四边形,∴OA=OC,AD∥BC,
∴∠EAO=∠FCO.
在△AOE与△COF中,∵∠EAO=∠FCO,OA=OC,∠AOE=∠COF,
∴△AOE≌△COF(ASA),
∴AE=CF=3cm.
同理可得△AOB≌△COD,△BOF≌△DOE,
∴S四边形EDCF=S四边形AEFB=15cm2.
故答案为3cm,15cm2.
15.
∵,,
∴,
设,,
在中,,
∴,
解得:(负值舍去),
∴,
∵原图形为中心对称图形,为对称中心,
∴.
16.(1)见详解
(2)见详解
(3)见详解
(1)解:如图,和点即为所求.
(2)解:如图,即为所求.
(3)解:如图,连接并延长,交于点,则点即为所求.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
