第5章二元一次方程组 单元基础达标测试题(含答案) 2024-2025学年北师大版八年级数学上册
文档属性
| 名称 | 第5章二元一次方程组 单元基础达标测试题(含答案) 2024-2025学年北师大版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 76.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 00:00:00 | ||
图片预览




文档简介
2024-2025学年北师大版八年级数学上册《第5章二元一次方程组》
单元基础达标测试题(附答案)
一、单选题(满分24分)
1.下列方程组中,是二元一次方程组的是( )
A. B. C. D.
2.是下面哪个二元一次方程的解( )
A. B. C. D.
3.用加减消元法解方程组时,得( )
A. B. C. D.
4.已知x、y满足方程组 ,则的值为( )
A.3 B. C.1 D.
5.已知直线与直线(k、b为常数,且)的交点纵坐标为5,则关于x、y的二元一次方程组的解为( )
A. B. C. D.
6.如图,在平面直角坐标系中、,若A、B两点关于x轴对称,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间的关系式是一次函数关系,图象如图所示,则弹簧本身的长度是( )
A.9cm B.10cm C.12.5cm D.20cm
8.《孙子算经》记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”(尺、寸是长度单位,1尺寸).意思是,现有一根木料,不知道其长度.用一根绳子去度量,绳子还剩余尺;将绳子对折再度量,长木还剩余1尺.问木料长多少?设绳子长为x尺,木料长为y尺,则可列方程组为( )
A. B.
C. D.
二、填空题(满分24分)
9.已知方程,用含y的代数式表示x,则 .
10.已知是二元一次方程的一个解,则k的值为 .
11.在同一直角坐标系中,直线和直线的交点坐标为 .
12.在平面直角坐标系内,若两条直线和的交点在第三象限的角平分线上,则b的值为 .
13.在中,当时,;当时,,则 , .
14.大刚和小亮到同一家超市购买水果,大刚买苹果和梨,共花了26元;小亮买苹果和梨,共花了11元.设苹果的售价为,梨的售价,则可列二元一次方程组为 .
15.已知关于x,y的二元一次方程的部分解如表1,关于x,y的二元一次方程的部分解如表2:
表1
x … 2 5 8 …
y … 2 …
表2
x … 2 5 8 11 …
y … 2 26 …
则关于x,y的二元一次方程组的解 .
16.如图,用10个大小、形状完全相同的小矩形,拼成一个宽为50cm的大矩形,设每个小矩形的长为xcm,宽为ycm,则可以列出的方程组是 .
三、解答题(满分72分)
17.解下列方程组:
(1) (2)
18.如果关于x,y的二元一次方程组的解互为相反数,求m的值.
19.已知一次函数的图象经过,两点.
(1)求此一次函数表达式;
(2)试判断点是否在此一次函数的图象上.
20.当m,n分别取何值时,方程组与的解相同?
21.某商场上周购进年冬奥会吉祥物冰墩墩与冬残奥会吉祥物雪容融两种毛绒玩具共个,共花去元,这两种吉祥物毛绒玩具的进价、售价如下表:
进价(元/个) 售价(元/个)
冰墩墩
雪容融
(1)求冰墩墩、雪容融这两种毛绒玩具分别购进了多少个?
(2)上周五售出这两种吉祥物毛绒玩具,共获得利元.那么这一天售出的冰墩墩、雪容融这两种毛绒玩具分别是多少个?
22.如图是甲地向乙地打长途电话所需要付的电话费(元)与通话时间(分)之间关系的图象(注意:通话时间不足分钟按分钟计费).
(1)通话分钟,要付电话费多少元?通话分钟要付电话费多少元?
(2)通话多少分钟内,所支付的电话费一样多?
(3)通话分钟应付电话费多少元?
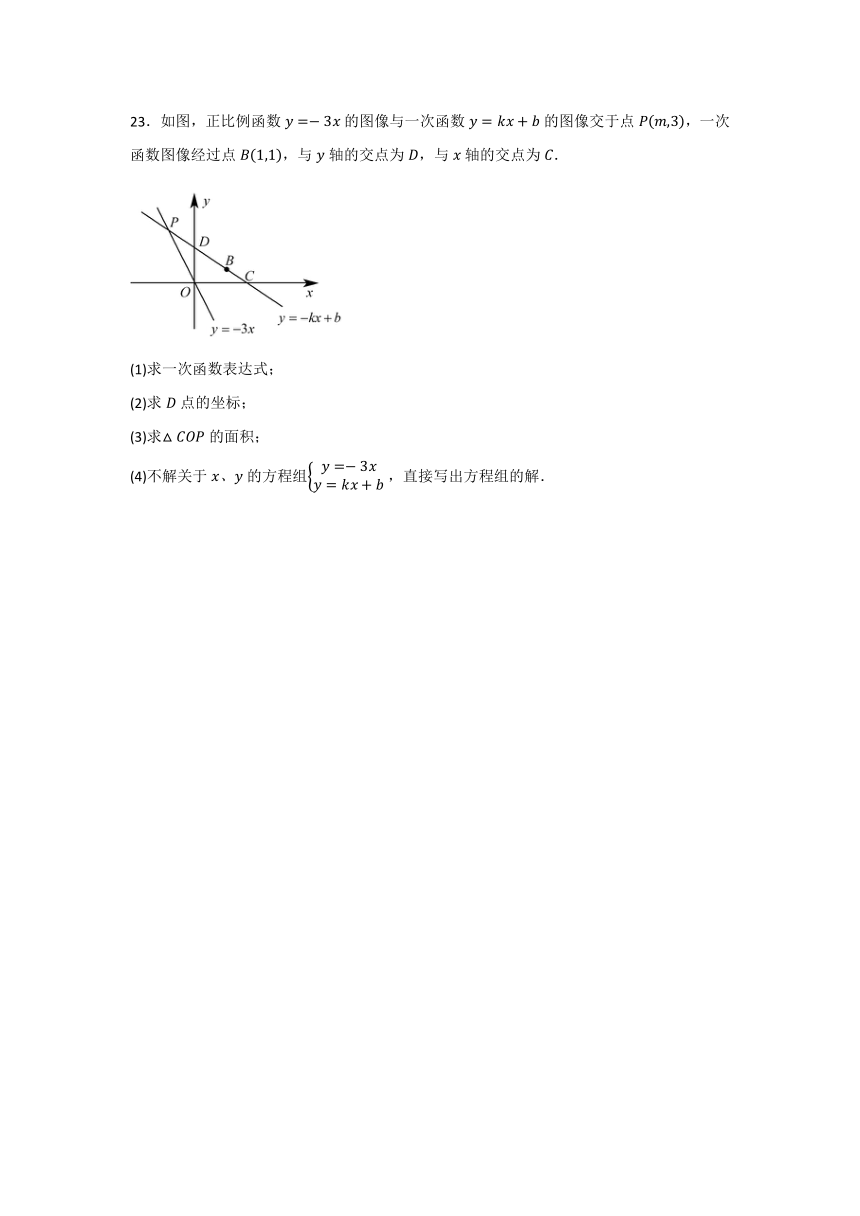
23.如图,正比例函数的图像与一次函数的图像交于点,一次函数图像经过点,与轴的交点为,与轴的交点为.
(1)求一次函数表达式;
(2)求点的坐标;
(3)求的面积;
(4)不解关于的方程组,直接写出方程组的解.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D B D B A D B B
1.解:A、含有3个未知数,不是二元一次方程组,不合题意;
B、含有二元二次方程,不是二元一次方程组,不合题意;
C、含有3个未知数且含有二次方程,不是二元一次方程组,不合题意;
D、符合二元一次方程组的定义,故该选项符合题意.
故选:D.
2.解:A、把代入得:,不是该二元一次方程的解,故本选项不符合题意;
B、把代入得:,是该二元一次方程的解,故本选项符合题意;
C、把代入得:,不是该二元一次方程的解,故本选项不符合题意;
D、把代入,不是该二元一次方程的解,故本选项不符合题意;
故选:B.
3.解:得:
即
故选D.
4.解:,
得:,
∴.
故选:B.
5.解:∵直线与直线(k、b为常数,且)的交点纵坐标为5,
∴,解得:,
∴直线与直线(k、b为常数,且)的交点纵坐标为,
∴关于x、y的二元一次方程组的解为.
故选A.
6.解:由题意得:,
解得:
∴点在第四象限
故选:D
7.解:设一次函数的解析式为y=kx+b.
将x=5,y=12.5,x=20,y=20代入得:
解得:k=,b=10.
故直线的解析式为y=x+10.
将x=0代入得:y=10.
故弹簧本身的长度是10cm.
故选:B.
8.解:∵绳子长为x尺,用一根绳子去度量,绳子还剩余尺
∴
∵将绳子对折再度量,长木还剩余1尺
∴
故选:B
9.解:,
,
.
故答案为:.
10.解:是二元一次方程的一个解,
将代入得:,
解得:,
故答案为:.
11.解:由题意得:,
解得:,
∴交点坐标为:,
故答案为:.
12.解:由题意可得:,
解得:,
∵交点在第三象限的角平分线上,
∴,
解得:b=-1,
故答案为:-1.
13.解:由题意,得:,解得:;
故答案为:2,0.
14.解:设苹果的售价为,梨的售价,根据大刚买苹果和梨,共花了26元;小亮买苹果和梨,共花了11元列出方程求解.
则.
故答案为:.
15.解:由表1可知,是的解,
由表2可知是的解,
∴关于x,y的二元一次方程组的解是:.
故答案为:.
16.解:由图可知小矩形的长为小矩形宽的4倍,所以,
小矩形的长与宽的和为50cm,所以
所以,可得方程组为:
故答案为:.
17.(1)解:,得
.
,得
,
.
将代入,得
,
.
所以,这个方程组的解是
.
(2)解:,得
.
,得
,
.
将代入,得
,
.
所以,这个方程组的解是
.
18.解:∵的解互为相反数,
∴③,
将③代入①得,
将代入③得,
将,代入②中得,
∴.
19.(1)解:设一次函数的解析式为,
∵,在函数图象上,
∴,
解得,
∴一次函数的解析式为:;
(2)解:由(1)知,函数解析式为:,
∴当时,,
∴点在一次函数的图象上.
20.】解:联立得:,
①②得:,
解得:,
把代入②得:,
代入得:,
解得:,.
21.(1)解:设购进冰墩墩毛绒玩具个,雪容融毛绒玩具个,
依题意得:,解得:.
∴购进冰墩墩毛绒玩具个,雪容融毛绒玩具个.
(2)解:设售出冰墩墩毛绒玩具个,雪容融毛绒玩具个,
依题意得:,
∴.
又∵,均为正整数,
∴或.
∴售出冰墩墩毛绒玩具个,雪容融毛绒玩具个或售出冰墩墩毛绒玩具个,雪容融毛绒玩具个.
22.解:(1)根据图象可知,通话1分钟时,要付电话费元,通话5分钟时,要付费元;
(2)根据图象可知,通话3分钟内,所支付的电话费一样多;
(3)当时,设
把代入
得:,
解得:,
所以
通话分钟,按4分钟计算,当时,,
故通话分钟应付电话费是元.
23.(1)解:∵正比例函数的图像与一次函数的图像交于点,
∴,解得:,
∴,
把和代入一次函数,得:
,解得, ,
∴ 一次函数解析式是.
(2)解:由(1)知一次函数表达式是 ,
令,则,
∴点.
(3)解:由(1)知一次函数解析式是,
令,,解得: ,
∴点,
∴,
∵,
∴的面积.
(4)解:∵正比例函数的图像与一次函数的图像交于点,
∴方程组的解为.
单元基础达标测试题(附答案)
一、单选题(满分24分)
1.下列方程组中,是二元一次方程组的是( )
A. B. C. D.
2.是下面哪个二元一次方程的解( )
A. B. C. D.
3.用加减消元法解方程组时,得( )
A. B. C. D.
4.已知x、y满足方程组 ,则的值为( )
A.3 B. C.1 D.
5.已知直线与直线(k、b为常数,且)的交点纵坐标为5,则关于x、y的二元一次方程组的解为( )
A. B. C. D.
6.如图,在平面直角坐标系中、,若A、B两点关于x轴对称,则点所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
7.弹簧的长度 y(cm)与所挂物体的质量 x(kg)之间的关系式是一次函数关系,图象如图所示,则弹簧本身的长度是( )
A.9cm B.10cm C.12.5cm D.20cm
8.《孙子算经》记载:“今有木,不知长短.引绳度之,余绳四尺五寸;屈绳量之,不足一尺.木长几何?”(尺、寸是长度单位,1尺寸).意思是,现有一根木料,不知道其长度.用一根绳子去度量,绳子还剩余尺;将绳子对折再度量,长木还剩余1尺.问木料长多少?设绳子长为x尺,木料长为y尺,则可列方程组为( )
A. B.
C. D.
二、填空题(满分24分)
9.已知方程,用含y的代数式表示x,则 .
10.已知是二元一次方程的一个解,则k的值为 .
11.在同一直角坐标系中,直线和直线的交点坐标为 .
12.在平面直角坐标系内,若两条直线和的交点在第三象限的角平分线上,则b的值为 .
13.在中,当时,;当时,,则 , .
14.大刚和小亮到同一家超市购买水果,大刚买苹果和梨,共花了26元;小亮买苹果和梨,共花了11元.设苹果的售价为,梨的售价,则可列二元一次方程组为 .
15.已知关于x,y的二元一次方程的部分解如表1,关于x,y的二元一次方程的部分解如表2:
表1
x … 2 5 8 …
y … 2 …
表2
x … 2 5 8 11 …
y … 2 26 …
则关于x,y的二元一次方程组的解 .
16.如图,用10个大小、形状完全相同的小矩形,拼成一个宽为50cm的大矩形,设每个小矩形的长为xcm,宽为ycm,则可以列出的方程组是 .
三、解答题(满分72分)
17.解下列方程组:
(1) (2)
18.如果关于x,y的二元一次方程组的解互为相反数,求m的值.
19.已知一次函数的图象经过,两点.
(1)求此一次函数表达式;
(2)试判断点是否在此一次函数的图象上.
20.当m,n分别取何值时,方程组与的解相同?
21.某商场上周购进年冬奥会吉祥物冰墩墩与冬残奥会吉祥物雪容融两种毛绒玩具共个,共花去元,这两种吉祥物毛绒玩具的进价、售价如下表:
进价(元/个) 售价(元/个)
冰墩墩
雪容融
(1)求冰墩墩、雪容融这两种毛绒玩具分别购进了多少个?
(2)上周五售出这两种吉祥物毛绒玩具,共获得利元.那么这一天售出的冰墩墩、雪容融这两种毛绒玩具分别是多少个?
22.如图是甲地向乙地打长途电话所需要付的电话费(元)与通话时间(分)之间关系的图象(注意:通话时间不足分钟按分钟计费).
(1)通话分钟,要付电话费多少元?通话分钟要付电话费多少元?
(2)通话多少分钟内,所支付的电话费一样多?
(3)通话分钟应付电话费多少元?
23.如图,正比例函数的图像与一次函数的图像交于点,一次函数图像经过点,与轴的交点为,与轴的交点为.
(1)求一次函数表达式;
(2)求点的坐标;
(3)求的面积;
(4)不解关于的方程组,直接写出方程组的解.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D B D B A D B B
1.解:A、含有3个未知数,不是二元一次方程组,不合题意;
B、含有二元二次方程,不是二元一次方程组,不合题意;
C、含有3个未知数且含有二次方程,不是二元一次方程组,不合题意;
D、符合二元一次方程组的定义,故该选项符合题意.
故选:D.
2.解:A、把代入得:,不是该二元一次方程的解,故本选项不符合题意;
B、把代入得:,是该二元一次方程的解,故本选项符合题意;
C、把代入得:,不是该二元一次方程的解,故本选项不符合题意;
D、把代入,不是该二元一次方程的解,故本选项不符合题意;
故选:B.
3.解:得:
即
故选D.
4.解:,
得:,
∴.
故选:B.
5.解:∵直线与直线(k、b为常数,且)的交点纵坐标为5,
∴,解得:,
∴直线与直线(k、b为常数,且)的交点纵坐标为,
∴关于x、y的二元一次方程组的解为.
故选A.
6.解:由题意得:,
解得:
∴点在第四象限
故选:D
7.解:设一次函数的解析式为y=kx+b.
将x=5,y=12.5,x=20,y=20代入得:
解得:k=,b=10.
故直线的解析式为y=x+10.
将x=0代入得:y=10.
故弹簧本身的长度是10cm.
故选:B.
8.解:∵绳子长为x尺,用一根绳子去度量,绳子还剩余尺
∴
∵将绳子对折再度量,长木还剩余1尺
∴
故选:B
9.解:,
,
.
故答案为:.
10.解:是二元一次方程的一个解,
将代入得:,
解得:,
故答案为:.
11.解:由题意得:,
解得:,
∴交点坐标为:,
故答案为:.
12.解:由题意可得:,
解得:,
∵交点在第三象限的角平分线上,
∴,
解得:b=-1,
故答案为:-1.
13.解:由题意,得:,解得:;
故答案为:2,0.
14.解:设苹果的售价为,梨的售价,根据大刚买苹果和梨,共花了26元;小亮买苹果和梨,共花了11元列出方程求解.
则.
故答案为:.
15.解:由表1可知,是的解,
由表2可知是的解,
∴关于x,y的二元一次方程组的解是:.
故答案为:.
16.解:由图可知小矩形的长为小矩形宽的4倍,所以,
小矩形的长与宽的和为50cm,所以
所以,可得方程组为:
故答案为:.
17.(1)解:,得
.
,得
,
.
将代入,得
,
.
所以,这个方程组的解是
.
(2)解:,得
.
,得
,
.
将代入,得
,
.
所以,这个方程组的解是
.
18.解:∵的解互为相反数,
∴③,
将③代入①得,
将代入③得,
将,代入②中得,
∴.
19.(1)解:设一次函数的解析式为,
∵,在函数图象上,
∴,
解得,
∴一次函数的解析式为:;
(2)解:由(1)知,函数解析式为:,
∴当时,,
∴点在一次函数的图象上.
20.】解:联立得:,
①②得:,
解得:,
把代入②得:,
代入得:,
解得:,.
21.(1)解:设购进冰墩墩毛绒玩具个,雪容融毛绒玩具个,
依题意得:,解得:.
∴购进冰墩墩毛绒玩具个,雪容融毛绒玩具个.
(2)解:设售出冰墩墩毛绒玩具个,雪容融毛绒玩具个,
依题意得:,
∴.
又∵,均为正整数,
∴或.
∴售出冰墩墩毛绒玩具个,雪容融毛绒玩具个或售出冰墩墩毛绒玩具个,雪容融毛绒玩具个.
22.解:(1)根据图象可知,通话1分钟时,要付电话费元,通话5分钟时,要付费元;
(2)根据图象可知,通话3分钟内,所支付的电话费一样多;
(3)当时,设
把代入
得:,
解得:,
所以
通话分钟,按4分钟计算,当时,,
故通话分钟应付电话费是元.
23.(1)解:∵正比例函数的图像与一次函数的图像交于点,
∴,解得:,
∴,
把和代入一次函数,得:
,解得, ,
∴ 一次函数解析式是.
(2)解:由(1)知一次函数表达式是 ,
令,则,
∴点.
(3)解:由(1)知一次函数解析式是,
令,,解得: ,
∴点,
∴,
∵,
∴的面积.
(4)解:∵正比例函数的图像与一次函数的图像交于点,
∴方程组的解为.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
