5.7用二元一次方程组确定一次函数表达式 同步训练题 (含答案) 2024-2025学年北师大版八年级数学上册
文档属性
| 名称 | 5.7用二元一次方程组确定一次函数表达式 同步训练题 (含答案) 2024-2025学年北师大版八年级数学上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 268.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 00:00:00 | ||
图片预览



文档简介
2024-2025学年北师大版八年级数学上册《5.7用二元一次方程组确定一次函数表达式》
同步训练题(附答案)
一、单选题
1.已知点在直线上,把直线向下平移2个单位长度,所得直线的表达式为( )
A. B. C. D.
2.将一次函数(是常数且)的图象向上平移4个单位长度,平移后的函数图象经过点,则的值为( )
A.2 B. C.2或4 D.或
3.若直线是由直线沿y轴平移得到的,且直线过点,则的值为( )
A. B. C.1 D.4
4.一次函数的自变量的取值范围是,相应函数值的取值范围是,则下列符合题意的函数是( )
A. B. C. D.
5.已知,直线和关于直线对称,若的解析式为,则的解析式是 ( )
A. B. C. D.
6.中国茶文化博大精深,祁门红茶在国内外享有盛誉,并被评为“中华十大名茶”.泡茶时,水温很有讲究.祁门红茶的冲泡温度一般建议在,为了冲泡出来的茶口感更佳,徽徽同学在煮茶时记录了水温(单位:)随时间(单位:)变化的数据,如下表.若水温的变化是均匀的,则水温达到的时间是( )
时间
水温
A. B. C. D.
7.某航空公司规定,旅客乘机所携带行李的质量与其托运费用y(元)的关系如图所示的一次函数图象确定,那么旅客可免费携带行李的最大质量为( )
A. B. C. D.
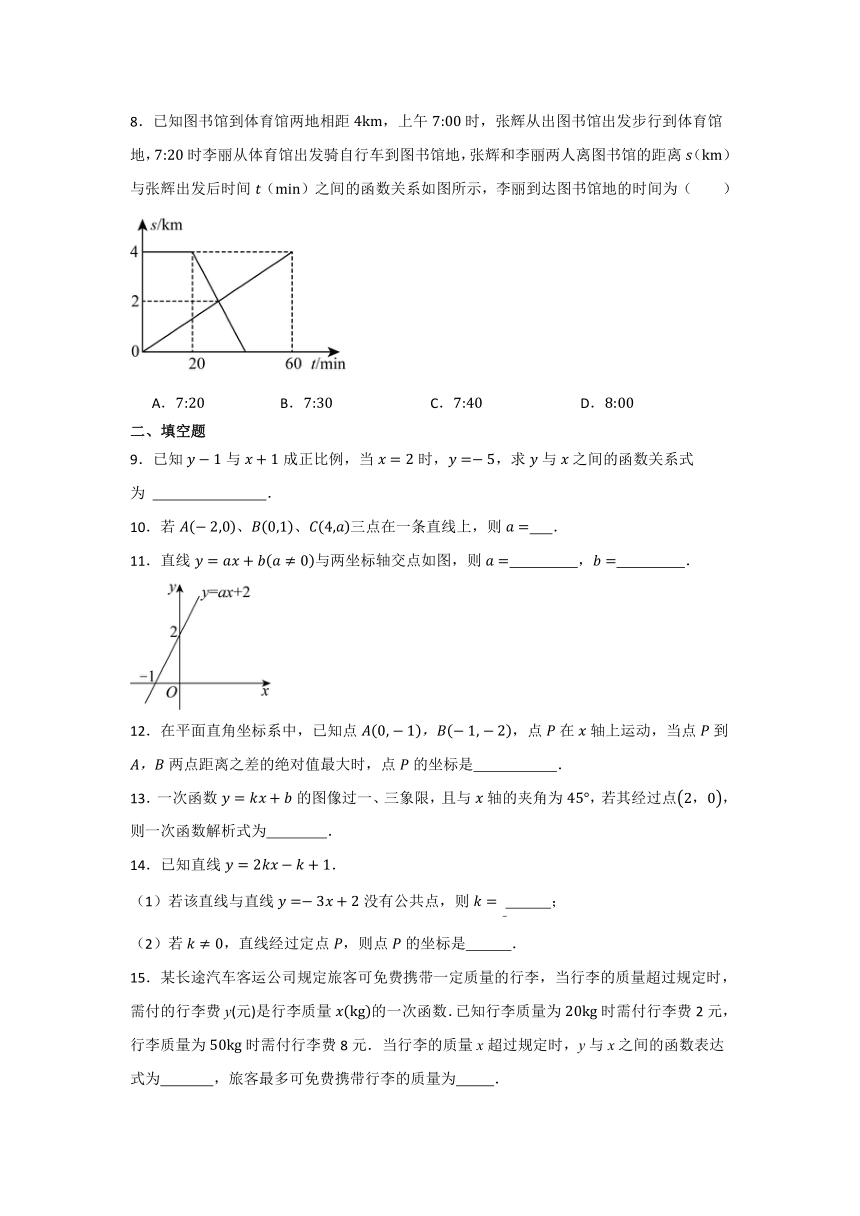
8.已知图书馆到体育馆两地相距,上午时,张辉从出图书馆出发步行到体育馆地,时李丽从体育馆出发骑自行车到图书馆地,张辉和李丽两人离图书馆的距离()与张辉出发后时间()之间的函数关系如图所示,李丽到达图书馆地的时间为( )
A. B. C. D.
二、填空题
9.已知与成正比例,当时,,求与之间的函数关系式为 .
10.若、、三点在一条直线上,则 .
11.直线与两坐标轴交点如图,则 , .
12.在平面直角坐标系中,已知点,点在轴上运动,当点到两点距离之差的绝对值最大时,点的坐标是 .
13.一次函数的图像过一、三象限,且与轴的夹角为,若其经过点,则一次函数解析式为 .
14.已知直线.
(1)若该直线与直线没有公共点,则 ;
(2)若,直线经过定点,则点的坐标是 .
15.某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量的一次函数.已知行李质量为时需付行李费2元,行李质量为时需付行李费8元.当行李的质量x超过规定时,y与x之间的函数表达式为 ,旅客最多可免费携带行李的质量为 .
16.如图,直线与直线交于点,则直线的解析式为: ;直线的解析式是: .
三、解答题
17.已知一次函数的图象经过点(3,2)和(1,4).
(1)画出此函数的图象;
(2)求此一次函数的表达式;
(3)若此函数的图象与x轴交于点A,与y轴交于点B,求线段AB的长.
18.如图,在平面直角坐标系中,直线与直线交点A的横坐标为2,将直线沿轴向下平移4个单位长度,得到直线,直线与轴交于点B,与直线交于点C,点C的纵坐标为.直线与轴交于点D.
(1)求点A与点C的坐标;
(2)求的面积.
19.人体标准体重随着人的身高的变化而变化,下表是标准体重与身高之间的函数关系:
身高 160 165 170 175 180 185
标准体重 56 59.5 63 66.5 70 73.5
(1)与之间的函数是_________函数;(填“正比例”“一次”或“其他”)
(2)求与之间的函数表达式;
(3)若马骥同学的身高为,求他的标准体重.
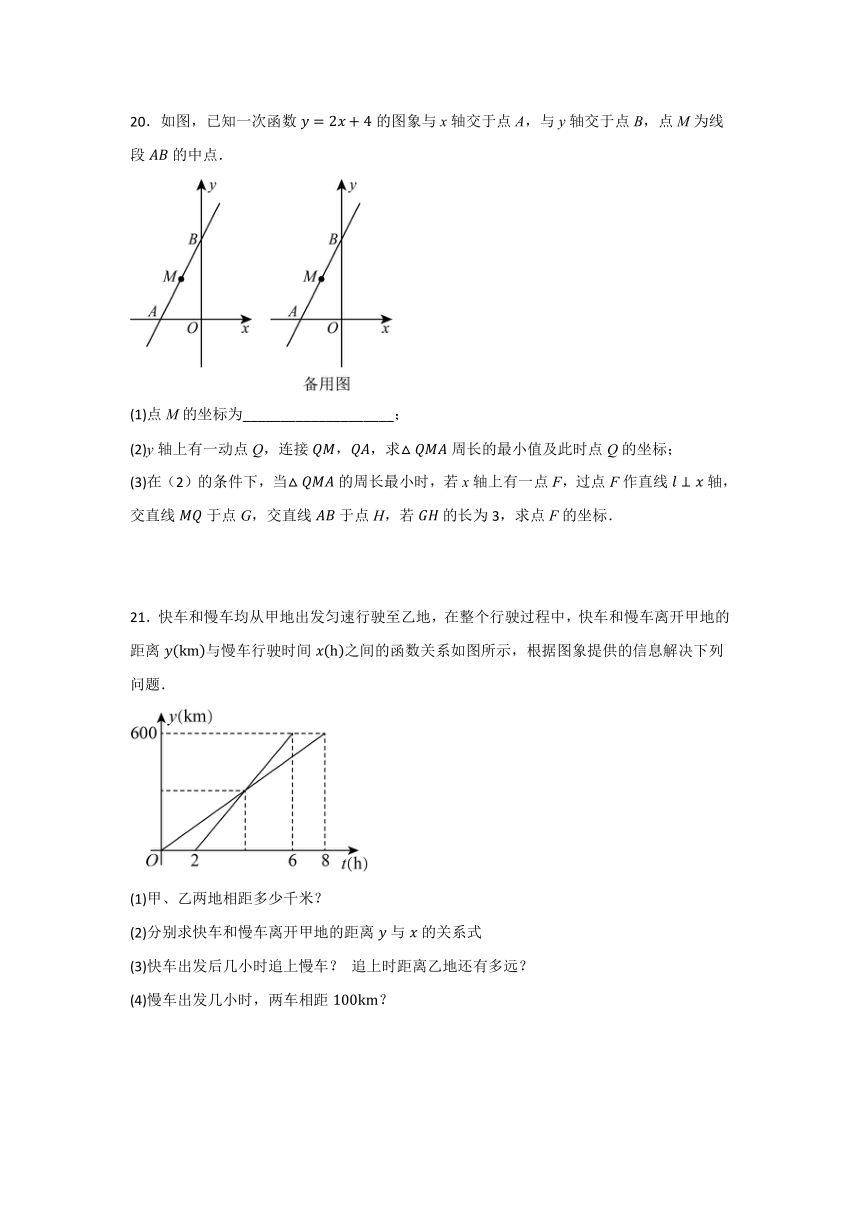
20.如图,已知一次函数的图象与x轴交于点A,与y轴交于点B,点M为线段的中点.
(1)点M的坐标为____________________;
(2)y轴上有一动点Q,连接,求周长的最小值及此时点Q的坐标;
(3)在(2)的条件下,当的周长最小时,若x轴上有一点F,过点F作直线轴,交直线于点G,交直线于点H,若的长为3,求点F的坐标.
21.快车和慢车均从甲地出发匀速行驶至乙地,在整个行驶过程中,快车和慢车离开甲地的距离与慢车行驶时间之间的函数关系如图所示,根据图象提供的信息解决下列问题.
(1)甲、乙两地相距多少千米?
(2)分别求快车和慢车离开甲地的距离与的关系式
(3)快车出发后几小时追上慢车? 追上时距离乙地还有多远?
(4)慢车出发几小时,两车相距?
22.如图,这是某种产品天的销售图象.图是产品日销售量(件)与时间(天)之间的函数关系图象,图是一件产品的销售利润(元)与时间(天)之间的函数关系图象.已知日销售利润日销售量一件产品的销售利润.
(1)第天的日销售量为______件.
(2)求第天销售一件产品的利润是多少元?
(3)求第天的日销售利润是多少元?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D B A D A B C C
1.解:将代入,得,
解得,
,
把直线向下平移2个单位长度,所得直线的表达式为:,
故选D.
2.解:一次函数(是常数且)的图象向上平移4个单位长度,则函数解析式变成:,
∵平移后的函数图象经过点,
∴,
解得:.
故选:B.
3.解:∵直线是由直线沿y轴平移得到的,
∴,
∵直线过点,
∴,
∴,
∴,
故选:A.
4.解:∵一次函数的自变量的取值范围是,相应函数值的取值范围是,
∴当时,一次函数过,,
∴,
解得,
∴一次函数解析式为;
当时,一次函数过,,
∴,
解得,
∴一次函数解析式为;
∴只有D选项符合题意.
故选:D.
5.解:令中得;令得
∴直线过点
∵直线与直线关于直线对称,
∴直线过点,
设直线的解析式为,则
解得
∴直线的解析式是,
故选A
6.解:根据表格中的数据可知,当时间增大温度升高,因此水温T是时间t的一次函数,
∴设水温T与时间t的关系式为:
,
把,代入得:
,
解得:,
∴,
把代入得:,
解得:,
∴水温达到的时间是,
故选:B.
7.解:设y与x的函数关系式为,把点,分别代入得,
由题意可知,
解得
所以y与x的函数关系式为,
当时,,
解得.
即旅客可免费携带行李的最大质量为,
故选:C.
8.解:依据题意,设张辉离图书馆的距离与时间的函数关系式为,
把,代入,得:
,
解得:,
张辉离图书馆的距离与时间的函数关系式为,
当时,,
设李丽离图书馆的距离与时间的函数关系式为,
把,和,代入,得:
,
解得:,
李丽离图书馆的距离与时间的函数关系式为,
令,于是有:
,
解得:,
李丽到达图书馆地的时间为,
故选:.
9.解:设正比例函数的关系式为,
把,代入,得,
解得:,
∴,
∴.
故答案为:.
10.解:设直线的解析式为,
则,解得
直线解析式为
把代入解得.
故答案为:3.
11.解:由图像知,直线与坐标轴交点的坐标为,,
∴
把代入,得
∴,
∴.
故答案为:2,2.
12.解:如图所示,
在中,,
∴当点三点共线时,,此时距离之差的绝对值最大,
∴设直线的解析式为,把点代入得,
∴,
解得,,
∴直线的解析式为,
当时,,
∴点的坐标为,
故答案为: .
13.解:∵一次函数的图像过一、三象限,且与轴的夹角为,
∴,
∵,
∴,
把,代入得,
解得,
∴.
故答案为:.
14. 解:(1)∵该直线与直线没有公共点,
∴,
解得:,
故答案为:;
(2)∵,
∴令,
解得:,
当时,,
∴定点的坐标是.
故答案为:.
15. 解:设行李费y(元)是行李质量的一次函数解析式为:,
把,代入可得:,
解得:,
∴y与x之间的函数表达式为.
当时, 解得:,
∴旅客最多可免费携带行李的质量为,
故答案为:;.
16.解:由图可知:直线经过点和原点,
设直线的解析式为,
把代入,得,
解得:,
∴,
当时,则,
解得:,
∴,
由图可知:直线经过点,,
设直线的解析式为,
把点,分别代入得:
,解得:,
∴直线的解析式为;
故答案为:;.
17.解:(1)如图所示:
(2)设一次函数的表达式为(,
由题意得,
解得,
所以此函数的表达式为;
(3)当x=0时,y=-x+5=5,
当y=0时,0=-x+5,解得:x=5,
所以点A的坐标为(5,0),点B的坐标为(0,5),
即,
在中,由勾股定理得.
18.(1)解:把代入,得,
∴A的坐标为.
∵将直线沿y轴向下平移4个单位长度,得到直线,
∴直线的解析式为,
∴时,,
∴.
将代入,得,
∴点C的坐标为.
(2)解:设直线的解析式为,
∵直线过、,
∴,解得,
∴直线的解析式为;
∵,
∴时,,
∴.
∵,
∴,
∴的面积.
19.(1)解:根据体重与身高之间的函数关系可知,身高每增加,体重增加,
则与之间的函数是一次函数.
(2)解:设与之间的函数表达式为,把代入,
得
解得
所以与之间的函数表达式为.
(3)解:当时,.
答:马骥同学的标准体重为.
20.(1)解:对于,
令,得;
令,得,
解得:,
∴,
∵点M为线段AB的中点,
∴,即,
(2)解:作点关于轴的对称点,连接交轴于点,连接,如图,
则,
∴,
∵,
∴,
∵点是固定点,
∴,
∴周长的最小值为,
又,
∴
∴,
∴周长的最小值为;
设直线的解析式为,
把代入,得,
,
解得,,
∴直线的解析式为,
当时,,
∴;
(3)解:设直线的解析式为,
把代入,得:
,
解得,,
∴直线的解析式为,
设点的坐标为
又过点的直线与交于点,
∴,
又直线和解析式与直线交于点,
∴,
∵,
∴,
整理得,,
解得,,或,
∴点的坐标为:或.
21.(1)解:由图可知,
甲、乙两地相距600千米.
(2)解:设慢车对应的函数解析式为:,
把代入,得
,
解得:,
∴慢车对应的函数解析式为:;
设快车对应的函数解析式为,
把,代入,得
,
解得:,
∴快车对应的函数解析式为.
(3)解:联立,得,
解得:,
,
,
答:快车出发后2小时追上慢车,追上时距离乙地还有.
(4)解:由题意可得,
当快车出发前两车相距,则,
解得:;
当快车出发后,追上慢车前,两车相距,则,
解得:;
当快车追上慢车后,到达乙地前,两车相距,则
解得:;
当快车到达乙地后,慢车到达乙地前,两车相距,则,
解得:;
综上,慢车出发小时或小时或小时或小时,两车相距.
22.(1)解:由图中的信息可得:第天的日销售量为件,
故答案为:;
(2)解:根据图,当时,设与之间的函数关系式为.
将坐标,分别代入,
得
解得
∴与之间的函数关系式为..
当时,,
∴第天销售一件产品的利润是元;
(3)解:根据图,当时,设与之间的函数关系式为.
将坐标,分别代入,
得
解得
∴与之间的函数关系式为..
当时,..
由(),得,
当时,,.
∴第天的日销售利润是(元)
同步训练题(附答案)
一、单选题
1.已知点在直线上,把直线向下平移2个单位长度,所得直线的表达式为( )
A. B. C. D.
2.将一次函数(是常数且)的图象向上平移4个单位长度,平移后的函数图象经过点,则的值为( )
A.2 B. C.2或4 D.或
3.若直线是由直线沿y轴平移得到的,且直线过点,则的值为( )
A. B. C.1 D.4
4.一次函数的自变量的取值范围是,相应函数值的取值范围是,则下列符合题意的函数是( )
A. B. C. D.
5.已知,直线和关于直线对称,若的解析式为,则的解析式是 ( )
A. B. C. D.
6.中国茶文化博大精深,祁门红茶在国内外享有盛誉,并被评为“中华十大名茶”.泡茶时,水温很有讲究.祁门红茶的冲泡温度一般建议在,为了冲泡出来的茶口感更佳,徽徽同学在煮茶时记录了水温(单位:)随时间(单位:)变化的数据,如下表.若水温的变化是均匀的,则水温达到的时间是( )
时间
水温
A. B. C. D.
7.某航空公司规定,旅客乘机所携带行李的质量与其托运费用y(元)的关系如图所示的一次函数图象确定,那么旅客可免费携带行李的最大质量为( )
A. B. C. D.
8.已知图书馆到体育馆两地相距,上午时,张辉从出图书馆出发步行到体育馆地,时李丽从体育馆出发骑自行车到图书馆地,张辉和李丽两人离图书馆的距离()与张辉出发后时间()之间的函数关系如图所示,李丽到达图书馆地的时间为( )
A. B. C. D.
二、填空题
9.已知与成正比例,当时,,求与之间的函数关系式为 .
10.若、、三点在一条直线上,则 .
11.直线与两坐标轴交点如图,则 , .
12.在平面直角坐标系中,已知点,点在轴上运动,当点到两点距离之差的绝对值最大时,点的坐标是 .
13.一次函数的图像过一、三象限,且与轴的夹角为,若其经过点,则一次函数解析式为 .
14.已知直线.
(1)若该直线与直线没有公共点,则 ;
(2)若,直线经过定点,则点的坐标是 .
15.某长途汽车客运公司规定旅客可免费携带一定质量的行李,当行李的质量超过规定时,需付的行李费y(元)是行李质量的一次函数.已知行李质量为时需付行李费2元,行李质量为时需付行李费8元.当行李的质量x超过规定时,y与x之间的函数表达式为 ,旅客最多可免费携带行李的质量为 .
16.如图,直线与直线交于点,则直线的解析式为: ;直线的解析式是: .
三、解答题
17.已知一次函数的图象经过点(3,2)和(1,4).
(1)画出此函数的图象;
(2)求此一次函数的表达式;
(3)若此函数的图象与x轴交于点A,与y轴交于点B,求线段AB的长.
18.如图,在平面直角坐标系中,直线与直线交点A的横坐标为2,将直线沿轴向下平移4个单位长度,得到直线,直线与轴交于点B,与直线交于点C,点C的纵坐标为.直线与轴交于点D.
(1)求点A与点C的坐标;
(2)求的面积.
19.人体标准体重随着人的身高的变化而变化,下表是标准体重与身高之间的函数关系:
身高 160 165 170 175 180 185
标准体重 56 59.5 63 66.5 70 73.5
(1)与之间的函数是_________函数;(填“正比例”“一次”或“其他”)
(2)求与之间的函数表达式;
(3)若马骥同学的身高为,求他的标准体重.
20.如图,已知一次函数的图象与x轴交于点A,与y轴交于点B,点M为线段的中点.
(1)点M的坐标为____________________;
(2)y轴上有一动点Q,连接,求周长的最小值及此时点Q的坐标;
(3)在(2)的条件下,当的周长最小时,若x轴上有一点F,过点F作直线轴,交直线于点G,交直线于点H,若的长为3,求点F的坐标.
21.快车和慢车均从甲地出发匀速行驶至乙地,在整个行驶过程中,快车和慢车离开甲地的距离与慢车行驶时间之间的函数关系如图所示,根据图象提供的信息解决下列问题.
(1)甲、乙两地相距多少千米?
(2)分别求快车和慢车离开甲地的距离与的关系式
(3)快车出发后几小时追上慢车? 追上时距离乙地还有多远?
(4)慢车出发几小时,两车相距?
22.如图,这是某种产品天的销售图象.图是产品日销售量(件)与时间(天)之间的函数关系图象,图是一件产品的销售利润(元)与时间(天)之间的函数关系图象.已知日销售利润日销售量一件产品的销售利润.
(1)第天的日销售量为______件.
(2)求第天销售一件产品的利润是多少元?
(3)求第天的日销售利润是多少元?
参考答案:
题号 1 2 3 4 5 6 7 8
答案 D B A D A B C C
1.解:将代入,得,
解得,
,
把直线向下平移2个单位长度,所得直线的表达式为:,
故选D.
2.解:一次函数(是常数且)的图象向上平移4个单位长度,则函数解析式变成:,
∵平移后的函数图象经过点,
∴,
解得:.
故选:B.
3.解:∵直线是由直线沿y轴平移得到的,
∴,
∵直线过点,
∴,
∴,
∴,
故选:A.
4.解:∵一次函数的自变量的取值范围是,相应函数值的取值范围是,
∴当时,一次函数过,,
∴,
解得,
∴一次函数解析式为;
当时,一次函数过,,
∴,
解得,
∴一次函数解析式为;
∴只有D选项符合题意.
故选:D.
5.解:令中得;令得
∴直线过点
∵直线与直线关于直线对称,
∴直线过点,
设直线的解析式为,则
解得
∴直线的解析式是,
故选A
6.解:根据表格中的数据可知,当时间增大温度升高,因此水温T是时间t的一次函数,
∴设水温T与时间t的关系式为:
,
把,代入得:
,
解得:,
∴,
把代入得:,
解得:,
∴水温达到的时间是,
故选:B.
7.解:设y与x的函数关系式为,把点,分别代入得,
由题意可知,
解得
所以y与x的函数关系式为,
当时,,
解得.
即旅客可免费携带行李的最大质量为,
故选:C.
8.解:依据题意,设张辉离图书馆的距离与时间的函数关系式为,
把,代入,得:
,
解得:,
张辉离图书馆的距离与时间的函数关系式为,
当时,,
设李丽离图书馆的距离与时间的函数关系式为,
把,和,代入,得:
,
解得:,
李丽离图书馆的距离与时间的函数关系式为,
令,于是有:
,
解得:,
李丽到达图书馆地的时间为,
故选:.
9.解:设正比例函数的关系式为,
把,代入,得,
解得:,
∴,
∴.
故答案为:.
10.解:设直线的解析式为,
则,解得
直线解析式为
把代入解得.
故答案为:3.
11.解:由图像知,直线与坐标轴交点的坐标为,,
∴
把代入,得
∴,
∴.
故答案为:2,2.
12.解:如图所示,
在中,,
∴当点三点共线时,,此时距离之差的绝对值最大,
∴设直线的解析式为,把点代入得,
∴,
解得,,
∴直线的解析式为,
当时,,
∴点的坐标为,
故答案为: .
13.解:∵一次函数的图像过一、三象限,且与轴的夹角为,
∴,
∵,
∴,
把,代入得,
解得,
∴.
故答案为:.
14. 解:(1)∵该直线与直线没有公共点,
∴,
解得:,
故答案为:;
(2)∵,
∴令,
解得:,
当时,,
∴定点的坐标是.
故答案为:.
15. 解:设行李费y(元)是行李质量的一次函数解析式为:,
把,代入可得:,
解得:,
∴y与x之间的函数表达式为.
当时, 解得:,
∴旅客最多可免费携带行李的质量为,
故答案为:;.
16.解:由图可知:直线经过点和原点,
设直线的解析式为,
把代入,得,
解得:,
∴,
当时,则,
解得:,
∴,
由图可知:直线经过点,,
设直线的解析式为,
把点,分别代入得:
,解得:,
∴直线的解析式为;
故答案为:;.
17.解:(1)如图所示:
(2)设一次函数的表达式为(,
由题意得,
解得,
所以此函数的表达式为;
(3)当x=0时,y=-x+5=5,
当y=0时,0=-x+5,解得:x=5,
所以点A的坐标为(5,0),点B的坐标为(0,5),
即,
在中,由勾股定理得.
18.(1)解:把代入,得,
∴A的坐标为.
∵将直线沿y轴向下平移4个单位长度,得到直线,
∴直线的解析式为,
∴时,,
∴.
将代入,得,
∴点C的坐标为.
(2)解:设直线的解析式为,
∵直线过、,
∴,解得,
∴直线的解析式为;
∵,
∴时,,
∴.
∵,
∴,
∴的面积.
19.(1)解:根据体重与身高之间的函数关系可知,身高每增加,体重增加,
则与之间的函数是一次函数.
(2)解:设与之间的函数表达式为,把代入,
得
解得
所以与之间的函数表达式为.
(3)解:当时,.
答:马骥同学的标准体重为.
20.(1)解:对于,
令,得;
令,得,
解得:,
∴,
∵点M为线段AB的中点,
∴,即,
(2)解:作点关于轴的对称点,连接交轴于点,连接,如图,
则,
∴,
∵,
∴,
∵点是固定点,
∴,
∴周长的最小值为,
又,
∴
∴,
∴周长的最小值为;
设直线的解析式为,
把代入,得,
,
解得,,
∴直线的解析式为,
当时,,
∴;
(3)解:设直线的解析式为,
把代入,得:
,
解得,,
∴直线的解析式为,
设点的坐标为
又过点的直线与交于点,
∴,
又直线和解析式与直线交于点,
∴,
∵,
∴,
整理得,,
解得,,或,
∴点的坐标为:或.
21.(1)解:由图可知,
甲、乙两地相距600千米.
(2)解:设慢车对应的函数解析式为:,
把代入,得
,
解得:,
∴慢车对应的函数解析式为:;
设快车对应的函数解析式为,
把,代入,得
,
解得:,
∴快车对应的函数解析式为.
(3)解:联立,得,
解得:,
,
,
答:快车出发后2小时追上慢车,追上时距离乙地还有.
(4)解:由题意可得,
当快车出发前两车相距,则,
解得:;
当快车出发后,追上慢车前,两车相距,则,
解得:;
当快车追上慢车后,到达乙地前,两车相距,则
解得:;
当快车到达乙地后,慢车到达乙地前,两车相距,则,
解得:;
综上,慢车出发小时或小时或小时或小时,两车相距.
22.(1)解:由图中的信息可得:第天的日销售量为件,
故答案为:;
(2)解:根据图,当时,设与之间的函数关系式为.
将坐标,分别代入,
得
解得
∴与之间的函数关系式为..
当时,,
∴第天销售一件产品的利润是元;
(3)解:根据图,当时,设与之间的函数关系式为.
将坐标,分别代入,
得
解得
∴与之间的函数关系式为..
当时,..
由(),得,
当时,,.
∴第天的日销售利润是(元)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
