期中复习试题(第11章--第13章) 2024--2025学年上学期初中数学人教版八年级上册
文档属性
| 名称 | 期中复习试题(第11章--第13章) 2024--2025学年上学期初中数学人教版八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 770.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-07 14:53:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期中复习试题(第11章--第13章)
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.观察下列图形,是轴对称图形的是( )
A. B. C. D.
2.等腰三角形的两条边长分别为8和4,则它的周长等于( )
A.12 B.16 C.20 D.16或20
3.在△ABC中,∠A=55°,∠B 比∠C大25° ,则∠B 等于( )
A.50° B.100° C.75° D.125°
4.如图,ABC和EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定的是( )
A.AB=ED B.AC=EF
C.BF=DC D.ACEF
5.一个多边形的每个内角均为150°,则这个多边形是( )
A.九边形 B.十边形 C.十二边形 D.十五边形
6.如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM ≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
A.SSS B.SAS C.AAS D.HL
7.如图所示,△ABC是等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是( )
①点 P 在∠A 的平分线上; ②AS=AR; ③QPAR; ④△BRP≌△QSP.
A.全部正确 B.①②正确 C.①②③正确 D.①③正确
8.如图,平面上有与,其中与相交于P点,如图,若,,,则的度数为( )
A. B. C. D.
9.如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
10.一个三角形的三个内角度数之比为,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
二、填空题
11.如图,△ABC≌△ADE,若∠CAE=41°,AC⊥DE,则∠C的度数为 .
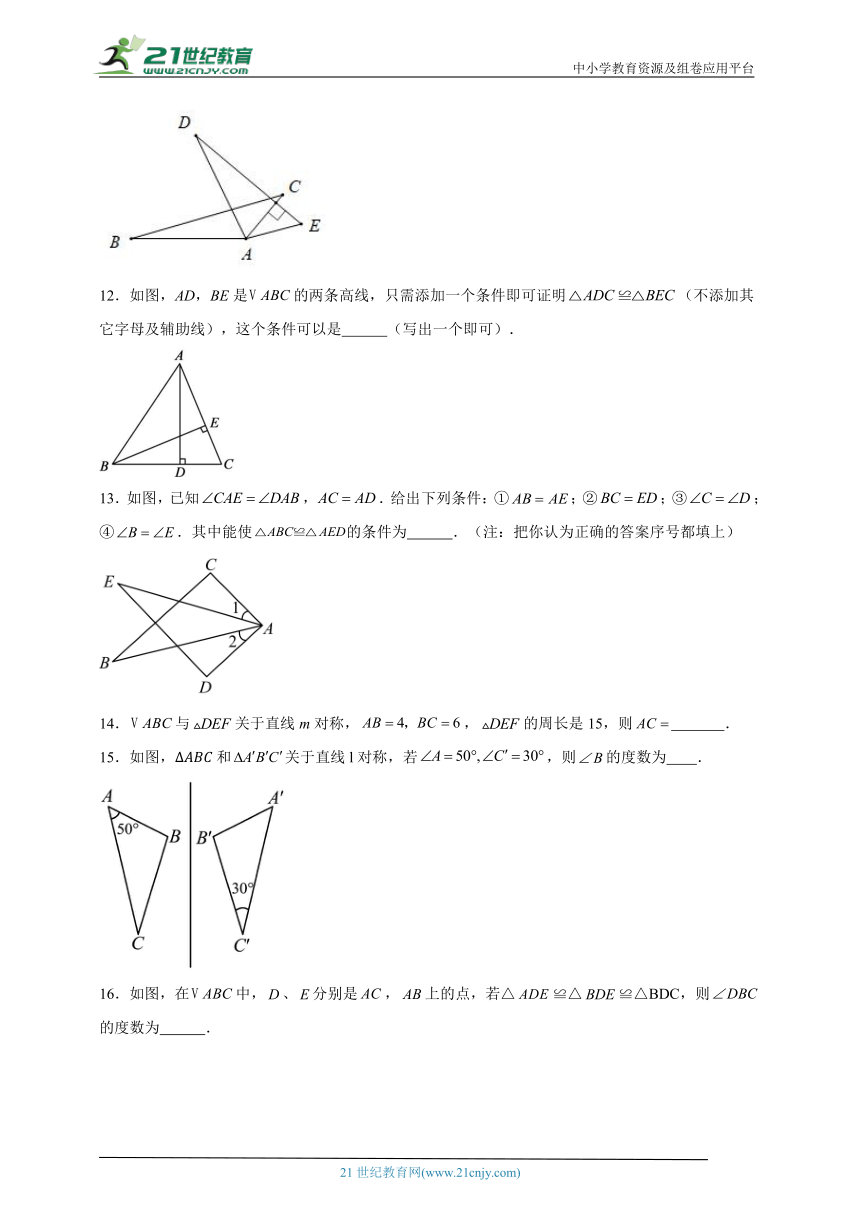
12.如图,AD,BE是的两条高线,只需添加一个条件即可证明(不添加其它字母及辅助线),这个条件可以是 (写出一个即可).
13.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为 .(注:把你认为正确的答案序号都填上)
14.与关于直线m对称,,的周长是15,则 .
15.如图,和关于直线l对称,若,则的度数为 .
16.如图,在中,、分别是,上的点,若△≌△≌△BDC,则的度数为 .
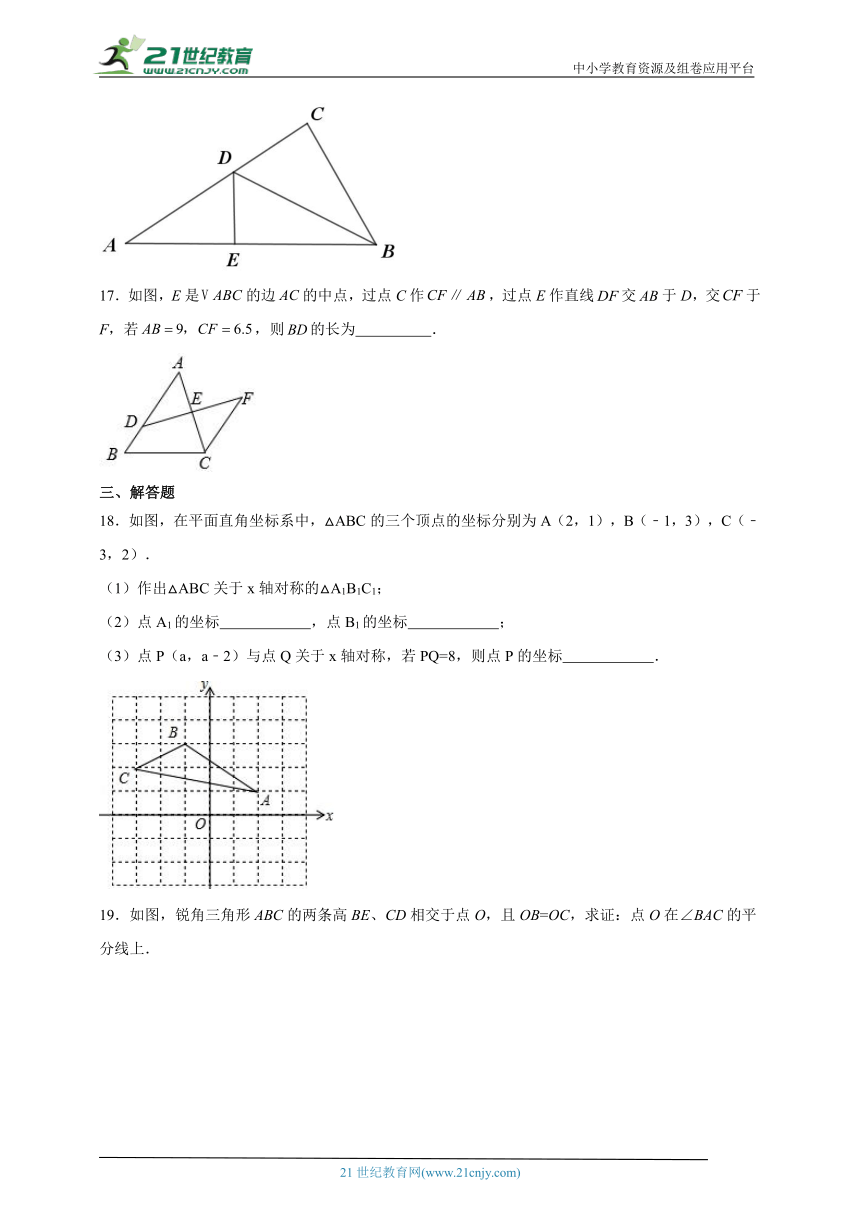
17.如图,E是的边的中点,过点C作,过点E作直线交于D,交于F,若,则的长为 .
三、解答题
18.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .
19.如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.
20.如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
21.如图所示,和都是等边三角形,且、、在同一直线上,连接交于,连接交于,连接.求证:
(1);
(2)的度数;
(3)判断的形状,并说明理由.
22.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)若与关于轴对称,点,,的对应点分别为,,,请画出并写出点,,的坐标;
(2)若点为平面内不与点重合的一点,与全等,请写出点的坐标.
23.如图,已知,平分的外角,为上一动点.
(1)若,求证:.
(2)在点运动过程中,试比较与的大小,并说明理由.
(3)若,于,且,,求长.
24.如图,为的角平分线,于点,于点,连接交于点.
(1)求证:垂直平分;
(2)若,猜测与间有何数量关系?请说明理由.
参考答案:
1.A
解:A、是轴对称图形,故本选项正确;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
2.C
解:等腰三角形的两边长分别为8和4,
当腰长为4,底边长为8时,,不满足三角形三边关系,不符合题意;
当腰长为8,底边长为4时,,满足三角形三边关系,符合题意,周长为,
3.C
∵∠B比∠C大25°,
∴设∠B=x,则∠C=x-25°,
∵∠A+∠B+∠C=180°,∠A=55°,
∴55°+x+x-25°=180°,
解得x=75°,
4.D
解:A.AB=ED,可用ASA判定,故错误;
B.AC=EF,可用AAS判定,故错误;
C.∵BF=DC,且FC为BC与FD的公共边,
∴BC=FD,
∴可用AAS判定,故错误;
D.ACEF,不能用AAA判定,故正确.
5.C
解:∵多边形的每个内角都等于150°,
∴多边形的每个外角都等于180°﹣150°=30°,
∴边数n=360°÷30°=12,
6.D
解:由作法可得OM=ON,PM⊥OM,PN⊥ON,
则∠PMO=∠PNO=90°,
在Rt△PMO和Rt△PNO中,,
所以△POM≌△PON(HL).
7.A
解:∵PR⊥AB于R,PS⊥AC于S
∴∠ARP=∠ASP=90°
∵PR=PS,AP=AP
∴Rt△ARP≌Rt△ASP
∴AR=AS,故②正确,∠BAP=∠CAP
∴AP是等边三角形的顶角的平分线,故①正确
∴AP是BC边上的高和中线,即点P是BC的中点
∵AQ=PQ
∴点Q是AC的中点
∴PQ是边AB对的中位线
∴PQ∥AB,故③正确
∵Q是AC的中点,
∴QC=QP,
∵∠C=60°,
∴△QPC是等边三角形,
∴PB=PC=PQ,
∵PR=PS,∠BRP=∠QSP=90°,
∴△BRP≌△QSP,故④正确
∴全部正确.
8.C
解:在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
9.D
解:∵中转站要到三条公路的距离都相等,
∴货物中转站必须是三条相交直线所组成的三角形的内角或外角平分线的交点,
而外角平分线有3个交点,内角平分线有一个交点,
如图,
∴货物中转站可以供选择的地址有4处.
10.B
解:∵三角形的三个内角度数之比为,
∴最大角度数为,
∴该三角形是直角三角形.
11.49°/49度
∵AC⊥DE,
∴∠AFE=90°,
∵∠CAE=41°,
∴∠E=90°-41°=49°,
∵△ABC≌△ADE,
∴∠C=∠E=49°.
故答案为:49°.
12.(答案不唯一)
解:添加,
AD,BE是的两条高线,
,
在与中,
.
故答案为:(答案不唯一).
13.①③④
解:∵,
∴,即,
①当时,
在和中,
,
∴;
②当时,不能判断;
③当时,
在和中,
,
∴;
④当时,
在和中,
,
∴;
综上分析可知,能使的条件是①③④.
故答案为:①③④.
14.5
解:∵与关于直线m对称,的周长是15,
∴的周长为15,
∵,
∴.
故答案为:5.
15.
解:∵和关于直线l对称,
∴∠C=
∴∠B=180°-∠A-∠C=100°
故答案为:100°.
16.
解:∵≌
∴∠A=∠DBE,∠DEA=∠DEB
∵∠DEA+∠DEB=180°
∴∠DEA=∠DEB=90°
∵≌△BDC
∴∠DBE=∠DBC,∠DEB=∠C=90°
∴∠A=∠DBE=∠DBC
∴∠DBC=90°÷3=30°
故答案为:30°.
17.2.5
证明:∵CF//AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE= EC,
在△ADE和 CFE中,
∴△ADE≌ CFE(AAS),
∴AD= CF= 6.5,
∵AB= 9,
∴BD= AB- AD=9- 6.5= 2.5,
故答案为: 2.5.
18.答案见解析.
(1)
(2)点的坐标为(2,-1),点的坐标为 (-1,-3) ;
(3)∵点P与Q关于y轴对称,
∴Q点为(-a,a-2),
又∵PQ=8,
∴a=4或a=-4,
∴a-2=2或a-2=-6.
∴P的坐标为 (4, 2)或(-4,-6);
19.证明见解析.
证明:∵BE、CD是△ABC的两条高
∴OD⊥AB,OE⊥AC,∠BDO=∠CEO=90°
在△BDO和△CEO中
∴△BDO≌△CEO
∴OD=OE
又∵OD⊥AB,OE⊥AC
∴点O在∠BAC的平分线上
20.见解析
(1)∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中,,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC;
(2)∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形.
21.(1)见解析
(2)
(3)等边三角形,见解析
(1)证明:和都是等边三角形,
,,,
,
则在和中,
,
,
;
(2)解:由(1)可知,,
,
,
,
,
,
;
(3)解:是等边三角形
理由:由(1)可知,,,
,
又,
则在和中,
,
,
,
是等边三角形.
22.(1)见解析,,,;(2),,
解:(1)如图所示,即为所求,,,
(2)点坐标为:,,.
23.(1)见解析
(2),见解析
(3)7
(1)证明:如图,在上取点,使,连接,
平分,
,
在和中,
,
,
,,
又,
,
,
,
;
(2)解:,
理由如下:
在(1)中可得,
,,
在中,由三角形三边关系可得,
,
,
即.
(3)解:如图(2),过作于点,
平分,
,
在和中,,,
,
,
在和中,,,
,
,
设,则,即,解得,
.
24.(1)见解析
(2),见解析
(1)证明:为的角平分线,,,
,,
,
,
,
点、都在的垂直平分线上,
垂直平分;
(2)解:,理由如下:
,平分,
,
,,
,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期中复习试题(第11章--第13章)
2024--2025学年上学期初中数学人教版八年级上册
一、单选题
1.观察下列图形,是轴对称图形的是( )
A. B. C. D.
2.等腰三角形的两条边长分别为8和4,则它的周长等于( )
A.12 B.16 C.20 D.16或20
3.在△ABC中,∠A=55°,∠B 比∠C大25° ,则∠B 等于( )
A.50° B.100° C.75° D.125°
4.如图,ABC和EDF中,∠B=∠D=90°,∠A=∠E,点B,F,C,D在同一条直线上,再增加一个条件,不能判定的是( )
A.AB=ED B.AC=EF
C.BF=DC D.ACEF
5.一个多边形的每个内角均为150°,则这个多边形是( )
A.九边形 B.十边形 C.十二边形 D.十五边形
6.如图,用三角尺可按下面方法画角平分线:在已知的∠AOB 的两边上分别取点M、N,使OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP.可证得△POM ≌△PON,OP平分∠AOB.以上依画法证明△POM≌△PON根据的是( )
A.SSS B.SAS C.AAS D.HL
7.如图所示,△ABC是等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,则四个结论正确的是( )
①点 P 在∠A 的平分线上; ②AS=AR; ③QPAR; ④△BRP≌△QSP.
A.全部正确 B.①②正确 C.①②③正确 D.①③正确
8.如图,平面上有与,其中与相交于P点,如图,若,,,则的度数为( )
A. B. C. D.
9.如图,直线表示三条相互交叉的公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有( )
A.1处 B.2处 C.3处 D.4处
10.一个三角形的三个内角度数之比为,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
二、填空题
11.如图,△ABC≌△ADE,若∠CAE=41°,AC⊥DE,则∠C的度数为 .
12.如图,AD,BE是的两条高线,只需添加一个条件即可证明(不添加其它字母及辅助线),这个条件可以是 (写出一个即可).
13.如图,已知,.给出下列条件:①;②;③;④.其中能使的条件为 .(注:把你认为正确的答案序号都填上)
14.与关于直线m对称,,的周长是15,则 .
15.如图,和关于直线l对称,若,则的度数为 .
16.如图,在中,、分别是,上的点,若△≌△≌△BDC,则的度数为 .
17.如图,E是的边的中点,过点C作,过点E作直线交于D,交于F,若,则的长为 .
三、解答题
18.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(2,1),B(﹣1,3),C(﹣3,2).
(1)作出△ABC关于x轴对称的△A1B1C1;
(2)点A1的坐标 ,点B1的坐标 ;
(3)点P(a,a﹣2)与点Q关于x轴对称,若PQ=8,则点P的坐标 .
19.如图,锐角三角形ABC的两条高BE、CD相交于点O,且OB=OC,求证:点O在∠BAC的平分线上.
20.如图,四边形ABCD中,∠A=∠B=90°,E是AB上一点,且AE=BC,∠1=∠2.
(1)证明:AB=AD+BC;
(2)判断△CDE的形状?并说明理由.
21.如图所示,和都是等边三角形,且、、在同一直线上,连接交于,连接交于,连接.求证:
(1);
(2)的度数;
(3)判断的形状,并说明理由.
22.如图,在平面直角坐标系中,的顶点坐标分别为,,.
(1)若与关于轴对称,点,,的对应点分别为,,,请画出并写出点,,的坐标;
(2)若点为平面内不与点重合的一点,与全等,请写出点的坐标.
23.如图,已知,平分的外角,为上一动点.
(1)若,求证:.
(2)在点运动过程中,试比较与的大小,并说明理由.
(3)若,于,且,,求长.
24.如图,为的角平分线,于点,于点,连接交于点.
(1)求证:垂直平分;
(2)若,猜测与间有何数量关系?请说明理由.
参考答案:
1.A
解:A、是轴对称图形,故本选项正确;
B、不是轴对称图形,故本选项错误;
C、不是轴对称图形,故本选项错误;
D、不是轴对称图形,故本选项错误.
2.C
解:等腰三角形的两边长分别为8和4,
当腰长为4,底边长为8时,,不满足三角形三边关系,不符合题意;
当腰长为8,底边长为4时,,满足三角形三边关系,符合题意,周长为,
3.C
∵∠B比∠C大25°,
∴设∠B=x,则∠C=x-25°,
∵∠A+∠B+∠C=180°,∠A=55°,
∴55°+x+x-25°=180°,
解得x=75°,
4.D
解:A.AB=ED,可用ASA判定,故错误;
B.AC=EF,可用AAS判定,故错误;
C.∵BF=DC,且FC为BC与FD的公共边,
∴BC=FD,
∴可用AAS判定,故错误;
D.ACEF,不能用AAA判定,故正确.
5.C
解:∵多边形的每个内角都等于150°,
∴多边形的每个外角都等于180°﹣150°=30°,
∴边数n=360°÷30°=12,
6.D
解:由作法可得OM=ON,PM⊥OM,PN⊥ON,
则∠PMO=∠PNO=90°,
在Rt△PMO和Rt△PNO中,,
所以△POM≌△PON(HL).
7.A
解:∵PR⊥AB于R,PS⊥AC于S
∴∠ARP=∠ASP=90°
∵PR=PS,AP=AP
∴Rt△ARP≌Rt△ASP
∴AR=AS,故②正确,∠BAP=∠CAP
∴AP是等边三角形的顶角的平分线,故①正确
∴AP是BC边上的高和中线,即点P是BC的中点
∵AQ=PQ
∴点Q是AC的中点
∴PQ是边AB对的中位线
∴PQ∥AB,故③正确
∵Q是AC的中点,
∴QC=QP,
∵∠C=60°,
∴△QPC是等边三角形,
∴PB=PC=PQ,
∵PR=PS,∠BRP=∠QSP=90°,
∴△BRP≌△QSP,故④正确
∴全部正确.
8.C
解:在和中,
,
∴,
∴,
∴,
∵,,
∴,
∴,
∵,
∴
∴,
∴,
∵,
∴,
9.D
解:∵中转站要到三条公路的距离都相等,
∴货物中转站必须是三条相交直线所组成的三角形的内角或外角平分线的交点,
而外角平分线有3个交点,内角平分线有一个交点,
如图,
∴货物中转站可以供选择的地址有4处.
10.B
解:∵三角形的三个内角度数之比为,
∴最大角度数为,
∴该三角形是直角三角形.
11.49°/49度
∵AC⊥DE,
∴∠AFE=90°,
∵∠CAE=41°,
∴∠E=90°-41°=49°,
∵△ABC≌△ADE,
∴∠C=∠E=49°.
故答案为:49°.
12.(答案不唯一)
解:添加,
AD,BE是的两条高线,
,
在与中,
.
故答案为:(答案不唯一).
13.①③④
解:∵,
∴,即,
①当时,
在和中,
,
∴;
②当时,不能判断;
③当时,
在和中,
,
∴;
④当时,
在和中,
,
∴;
综上分析可知,能使的条件是①③④.
故答案为:①③④.
14.5
解:∵与关于直线m对称,的周长是15,
∴的周长为15,
∵,
∴.
故答案为:5.
15.
解:∵和关于直线l对称,
∴∠C=
∴∠B=180°-∠A-∠C=100°
故答案为:100°.
16.
解:∵≌
∴∠A=∠DBE,∠DEA=∠DEB
∵∠DEA+∠DEB=180°
∴∠DEA=∠DEB=90°
∵≌△BDC
∴∠DBE=∠DBC,∠DEB=∠C=90°
∴∠A=∠DBE=∠DBC
∴∠DBC=90°÷3=30°
故答案为:30°.
17.2.5
证明:∵CF//AB,
∴∠ADE=∠F,∠FCE=∠A,
∵点E为AC的中点,
∴AE= EC,
在△ADE和 CFE中,
∴△ADE≌ CFE(AAS),
∴AD= CF= 6.5,
∵AB= 9,
∴BD= AB- AD=9- 6.5= 2.5,
故答案为: 2.5.
18.答案见解析.
(1)
(2)点的坐标为(2,-1),点的坐标为 (-1,-3) ;
(3)∵点P与Q关于y轴对称,
∴Q点为(-a,a-2),
又∵PQ=8,
∴a=4或a=-4,
∴a-2=2或a-2=-6.
∴P的坐标为 (4, 2)或(-4,-6);
19.证明见解析.
证明:∵BE、CD是△ABC的两条高
∴OD⊥AB,OE⊥AC,∠BDO=∠CEO=90°
在△BDO和△CEO中
∴△BDO≌△CEO
∴OD=OE
又∵OD⊥AB,OE⊥AC
∴点O在∠BAC的平分线上
20.见解析
(1)∵∠1=∠2,
∴DE=CE,
∵在RT△ADE和RT△BEC中,,
∴RT△ADE≌RT△BEC,(HL)
∴AD=BE,
∵AB=AE+BE,
∴AB=AD+BC;
(2)∵RT△ADE≌RT△BEC,
∴∠AED=∠BCE,
∵∠BCE+∠CEB=90°,
∴∠CEB+∠AED=90°,
∴∠DEC=90°,
∴△CDE为等腰直角三角形.
21.(1)见解析
(2)
(3)等边三角形,见解析
(1)证明:和都是等边三角形,
,,,
,
则在和中,
,
,
;
(2)解:由(1)可知,,
,
,
,
,
,
;
(3)解:是等边三角形
理由:由(1)可知,,,
,
又,
则在和中,
,
,
,
是等边三角形.
22.(1)见解析,,,;(2),,
解:(1)如图所示,即为所求,,,
(2)点坐标为:,,.
23.(1)见解析
(2),见解析
(3)7
(1)证明:如图,在上取点,使,连接,
平分,
,
在和中,
,
,
,,
又,
,
,
,
;
(2)解:,
理由如下:
在(1)中可得,
,,
在中,由三角形三边关系可得,
,
,
即.
(3)解:如图(2),过作于点,
平分,
,
在和中,,,
,
,
在和中,,,
,
,
设,则,即,解得,
.
24.(1)见解析
(2),见解析
(1)证明:为的角平分线,,,
,,
,
,
,
点、都在的垂直平分线上,
垂直平分;
(2)解:,理由如下:
,平分,
,
,,
,
,
,
,
,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
