人教版八年级数学下册18.2.2菱形—菱形的性质及判定定理课件)(25张PPT)
文档属性
| 名称 | 人教版八年级数学下册18.2.2菱形—菱形的性质及判定定理课件)(25张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 21:36:21 | ||
图片预览




文档简介
课件25张PPT。18.2.2 菱形第十八章 平行四边形 —菱形的性质及判定定理1. 经历菱形的概念、性质、判定定理的发现过程,掌握菱形的性质定理 “菱形的四条边都相等” ,“菱形的对角线互相垂直, 并且每条对角线平分一组对角” ;
2. 掌握菱形的判定定理“四条边相等的四边形是菱形”,“对角线互相垂直的平行四边形是菱形” ;
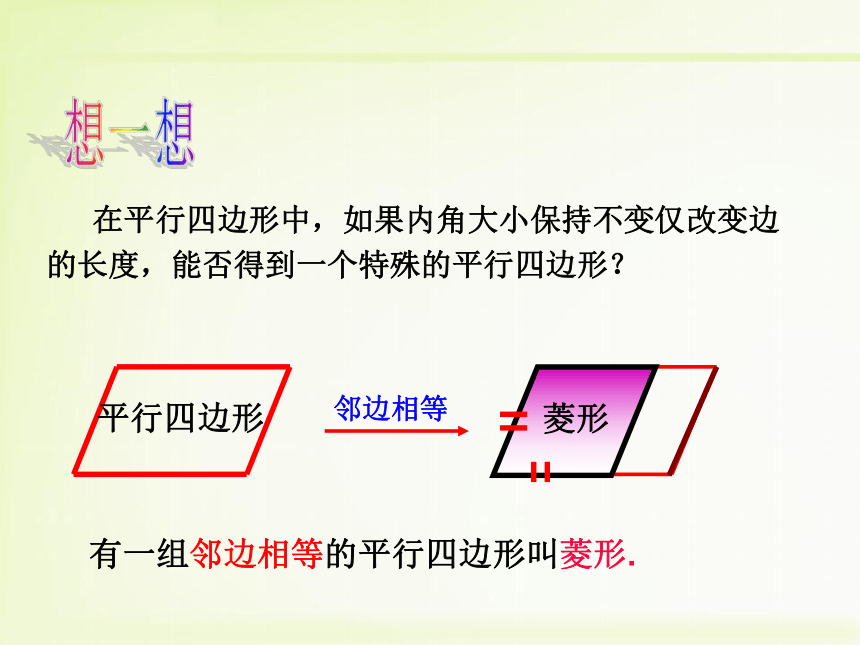
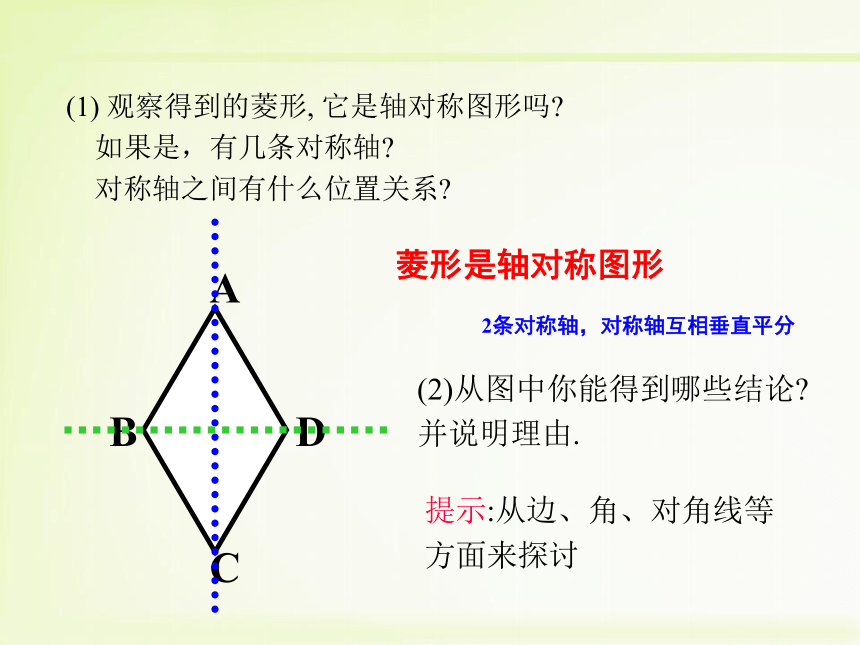
3. 能够运用菱形的知识解决简单的具体问题. 前面我们学习了平行四边形和矩形,知道如果平行四边形有一个角是直角时, 成为什么图形 ?矩形, 由角变化得到 如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?想一想 在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形? 平行四边形 菱形 菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.菱形是轴对称图形(2)从图中你能得到哪些结论?并说明理由.提示:从边、角、对角线等方面来探讨 (1) 观察得到的菱形, 它是轴对称图形吗?
如果是,有几条对称轴?
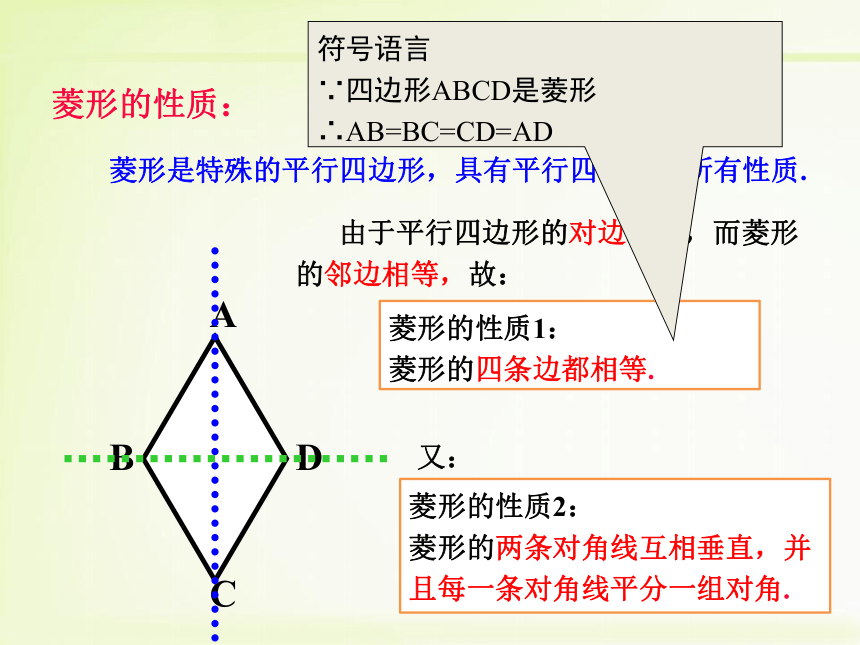
对称轴之间有什么位置关系?2条对称轴,对称轴互相垂直平分 由于平行四边形的对边相等,而菱形的邻边相等,故:菱形的性质2:
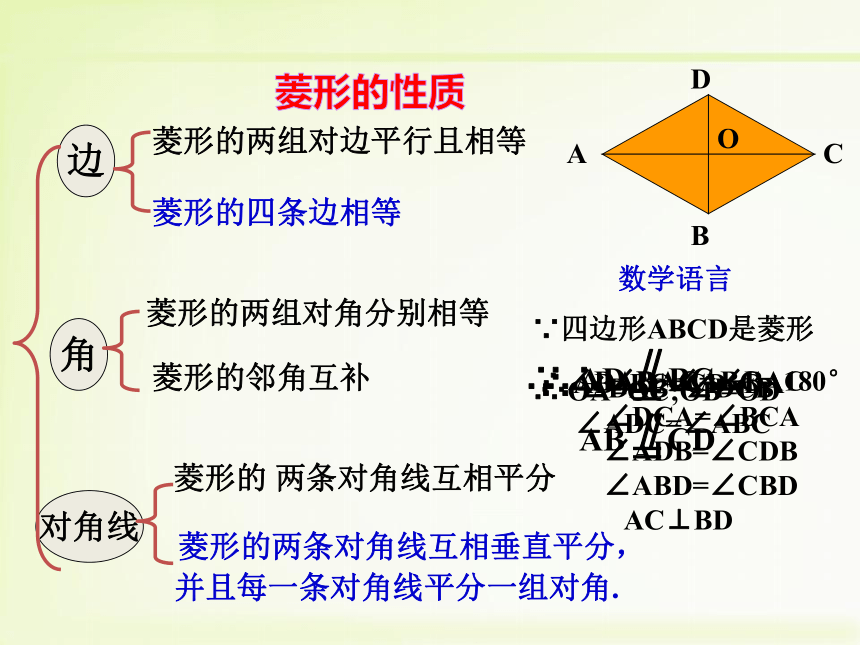
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质:菱形的性质1:
菱形的四条边都相等.又:符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
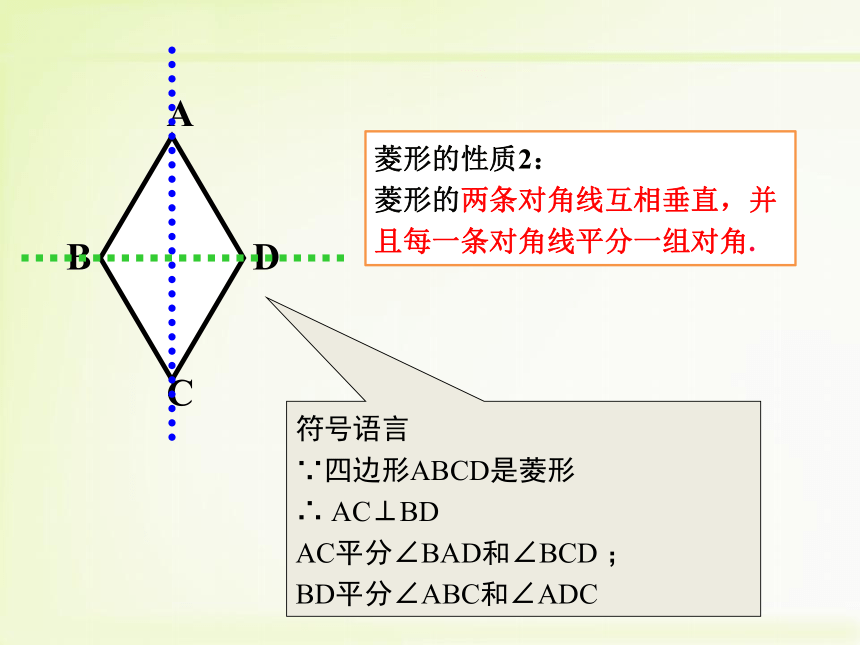
符号语言
∵四边形ABCD是菱形
∴ AC⊥BD
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角数学语言菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补 菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD ∴ OA=OC;OB=OD∴ ∠DAB=∠DCB
∠ADC=∠ABC ∴ ∠DAB+∠ABC= 180° 菱形的性质已知:如图,菱形ABCD的对角线AC和BD相交于点O.证明:∵四边形ABCD是菱形在△ABD中, BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ; AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC . 证一证想一想 我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么? 那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.根据定义得:命题:有四条边相等的四边形是菱形.已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵AB=BC=CD=DA∴四边形ABCD是菱形数学语言菱形的判定定理1:探究 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形?猜想:对角线互相垂直的平行四边形是菱形.命题:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC ∴ 平行四边形ABCD是菱形求证:平行四边形ABCD是菱形已知:在平行四边形ABCD中,AC ⊥ BD对角线互相垂直的平行四边形是菱形.数学语言菱形的判定定理2:∵在□ABCD中,AC⊥BD∴ □ABCD是菱形菱形常用的判定方法:有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形有四条边相等的四边形是菱形下列三个图形都是菱形, 正确吗? 为什么?有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?1、如图,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠ EAF=60°, ∠ BAE=18°, 求∠ CEF的度数.2、已知:如图, 四边形ABCD是边长为13cm的菱形, 其中对角线BD长10cm.求: (1)对角线AC的长度 (2)菱形的面积解: (1)∵四边形ABCD是菱形,∴∠AED=90°,∴AC=2AE=2×12=24(cm).=2×△ABD的面积解:(2) 菱形ABCD的面积
=△ABD的面积+△CBD的面积求: (2)菱形的面积 由此可进一步推导得出:
对角线互相垂直的四边形的面积都等于两条对角线乘积的一半.1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?教材P58,练习第2、3题.作 业
2. 掌握菱形的判定定理“四条边相等的四边形是菱形”,“对角线互相垂直的平行四边形是菱形” ;
3. 能够运用菱形的知识解决简单的具体问题. 前面我们学习了平行四边形和矩形,知道如果平行四边形有一个角是直角时, 成为什么图形 ?矩形, 由角变化得到 如果从边的角度,将平行四边形特殊化,又会得到什么特殊的四边形呢?想一想 在平行四边形中,如果内角大小保持不变仅改变边的长度,能否得到一个特殊的平行四边形? 平行四边形 菱形 菱形具有工整,匀称,美观等许多优点,常被人们用在图案设计上.菱形是轴对称图形(2)从图中你能得到哪些结论?并说明理由.提示:从边、角、对角线等方面来探讨 (1) 观察得到的菱形, 它是轴对称图形吗?
如果是,有几条对称轴?
对称轴之间有什么位置关系?2条对称轴,对称轴互相垂直平分 由于平行四边形的对边相等,而菱形的邻边相等,故:菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形是特殊的平行四边形,具有平行四边形的所有性质.菱形的性质:菱形的性质1:
菱形的四条边都相等.又:符号语言
∵四边形ABCD是菱形
∴AB=BC=CD=AD
符号语言
∵四边形ABCD是菱形
∴ AC⊥BD
AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC菱形的性质2:
菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.菱形的 两条对角线互相平分菱形的两组对边平行且相等边对角线角数学语言菱形的四条边相等菱形的两组对角分别相等菱形的邻角互补 菱形的两条对角线互相垂直平分,
并且每一条对角线平分一组对角.∵四边形ABCD是菱形 ∴ AB=BC=CD=DA∴ ∠DAC=∠BAC
∠DCA=∠BCA
∠ADB=∠CDB
∠ABD=∠CBD
AC⊥BD ∴ OA=OC;OB=OD∴ ∠DAB=∠DCB
∠ADC=∠ABC ∴ ∠DAB+∠ABC= 180° 菱形的性质已知:如图,菱形ABCD的对角线AC和BD相交于点O.证明:∵四边形ABCD是菱形在△ABD中, BO=DO∴AB=AD(菱形的四条边都相等)∴AC⊥BD,AC平分∠BAD同理: AC平分∠BCD;
BD平分∠ABC和∠ADC求证:AC⊥BD ; AC平分∠BAD和∠BCD ;
BD平分∠ABC和∠ADC . 证一证想一想 我们在学习平行四边形的判定和矩形的判定时,我们首先想到的第一种方法是什么? 那么类比着它们,菱形的第一种判定方法是什么?一组邻边相等的平行四边形是菱形.根据定义得:命题:有四条边相等的四边形是菱形.已知:在四边形ABCD中, AB=BC=CD=DA.
求证:四边形ABCD是菱形证明:∵AB=CD,AD=BC∴四边形ABCD是平行四边形又∵AB=AD,∴四边形ABCD是菱形四条边都相等的四边形是菱形.∵AB=BC=CD=DA∴四边形ABCD是菱形数学语言菱形的判定定理1:探究 用一长一短两根细木条,在它们的中点处固定一个小钉,做成一个可以转动的十字,四周围上一根橡皮筋,做成一个四边形. 转动木条,这个四边形什么时候变成菱形?猜想:对角线互相垂直的平行四边形是菱形.命题:对角线互相垂直的平行四边形是菱形.证明:∵四边形ABCD是平行四边形∴OA=OC又∵AC⊥BD; ∴BA=BC ∴ 平行四边形ABCD是菱形求证:平行四边形ABCD是菱形已知:在平行四边形ABCD中,AC ⊥ BD对角线互相垂直的平行四边形是菱形.数学语言菱形的判定定理2:∵在□ABCD中,AC⊥BD∴ □ABCD是菱形菱形常用的判定方法:有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形有四条边相等的四边形是菱形下列三个图形都是菱形, 正确吗? 为什么?有一组邻边相等的平行四边形叫做菱形对角线互相垂直的平行四边形是菱形 有四条边相等的四边形是菱形有同学是这样做的:将一张长方形的纸对折、再对折,然后沿图中的虚线剪下,打开即可. 你知道其中的道理吗? 如何利用折纸、剪切的方法,既快又准确地剪出一个菱形的纸片?1、如图,菱形ABCD中,E、F分别是BC、CD上的点,且∠B=∠ EAF=60°, ∠ BAE=18°, 求∠ CEF的度数.2、已知:如图, 四边形ABCD是边长为13cm的菱形, 其中对角线BD长10cm.求: (1)对角线AC的长度 (2)菱形的面积解: (1)∵四边形ABCD是菱形,∴∠AED=90°,∴AC=2AE=2×12=24(cm).=2×△ABD的面积解:(2) 菱形ABCD的面积
=△ABD的面积+△CBD的面积求: (2)菱形的面积 由此可进一步推导得出:
对角线互相垂直的四边形的面积都等于两条对角线乘积的一半.1.你的收获是什么?你的困惑是什么?
2.你会用类比的学习方法学习特殊四边形知识吗?教材P58,练习第2、3题.作 业
