人教版八年级数学下册18.2.3正方形—正方形的性质及判定定理课件
文档属性
| 名称 | 人教版八年级数学下册18.2.3正方形—正方形的性质及判定定理课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 21:42:08 | ||
图片预览


文档简介
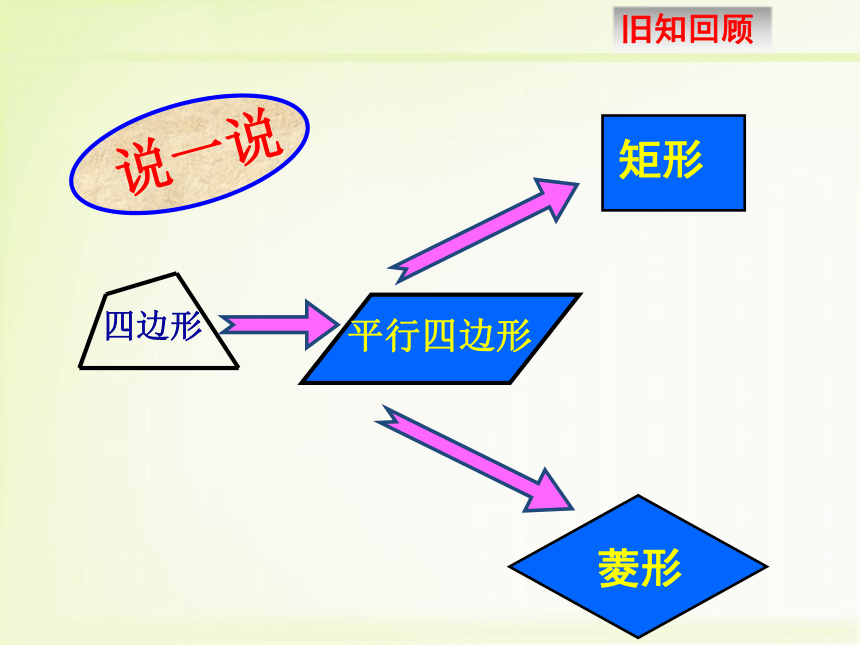
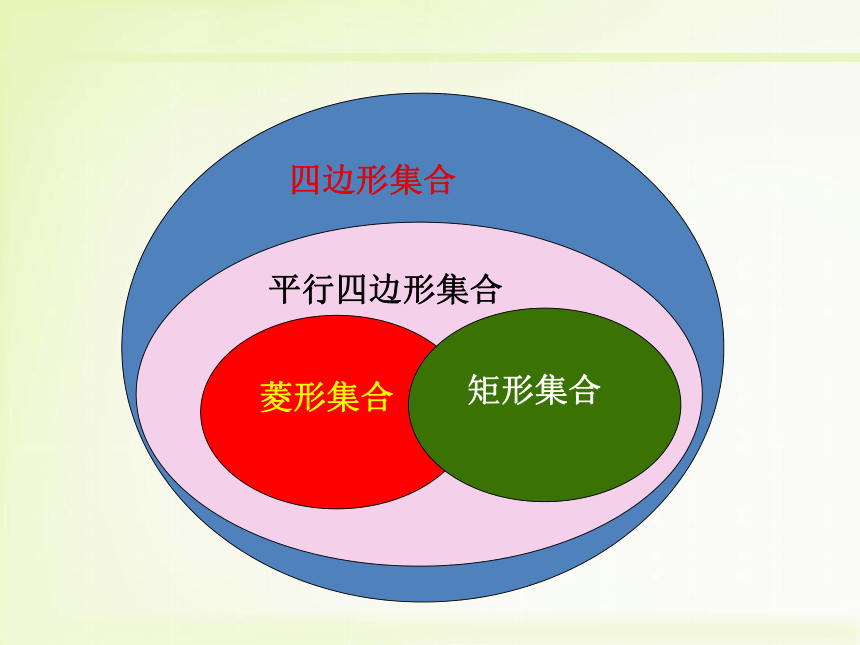
课件17张PPT。18.2.3 正方形第十八章 平行四边形 —正方形的性质及判定定理四边形矩形平行四边形菱形说一说1. 理解并掌握正方形的概念、性质及判定;
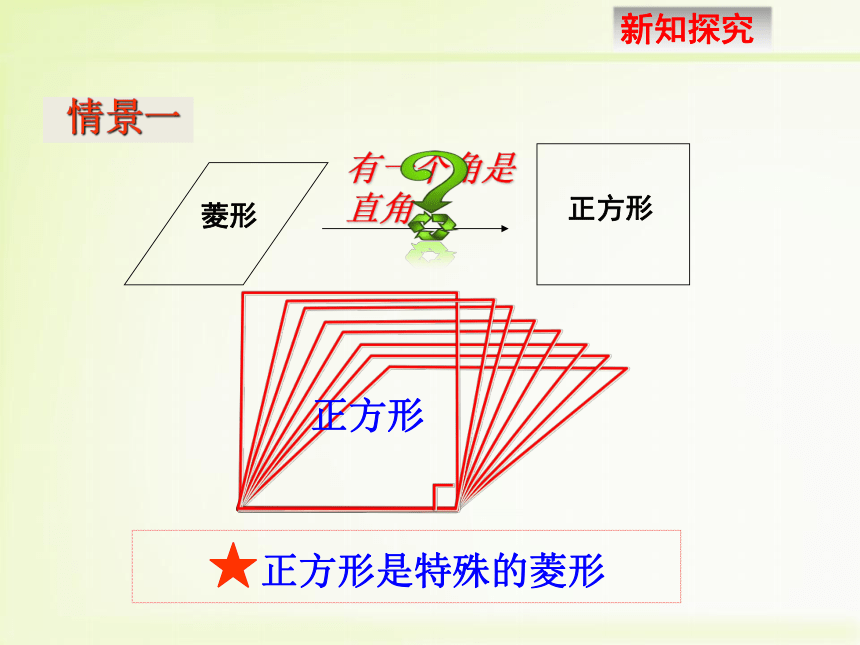
2. 经历探索正方形有关性质和判别条件的过程,了解正方形与矩形、菱形的关系.正方形正方形有一个角是
直角
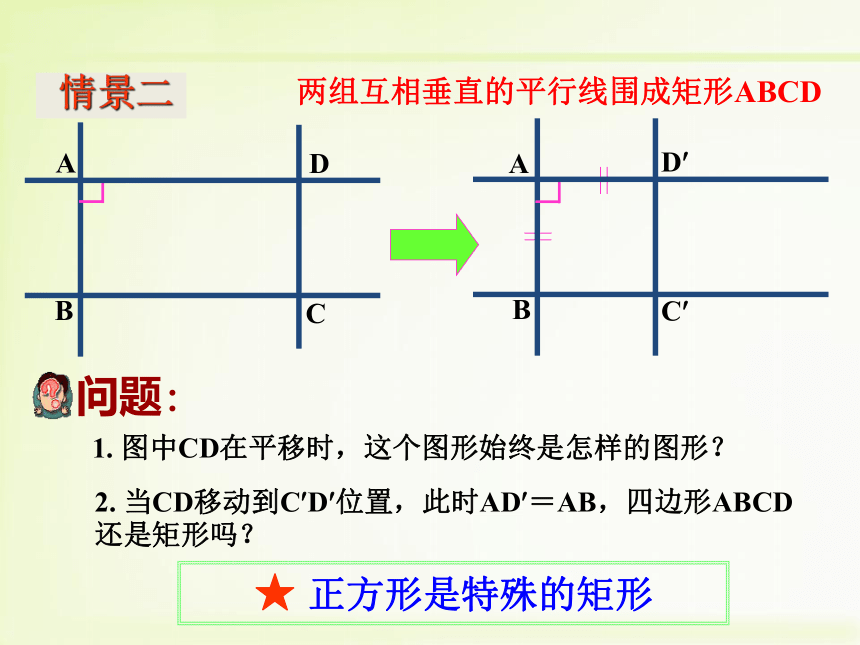
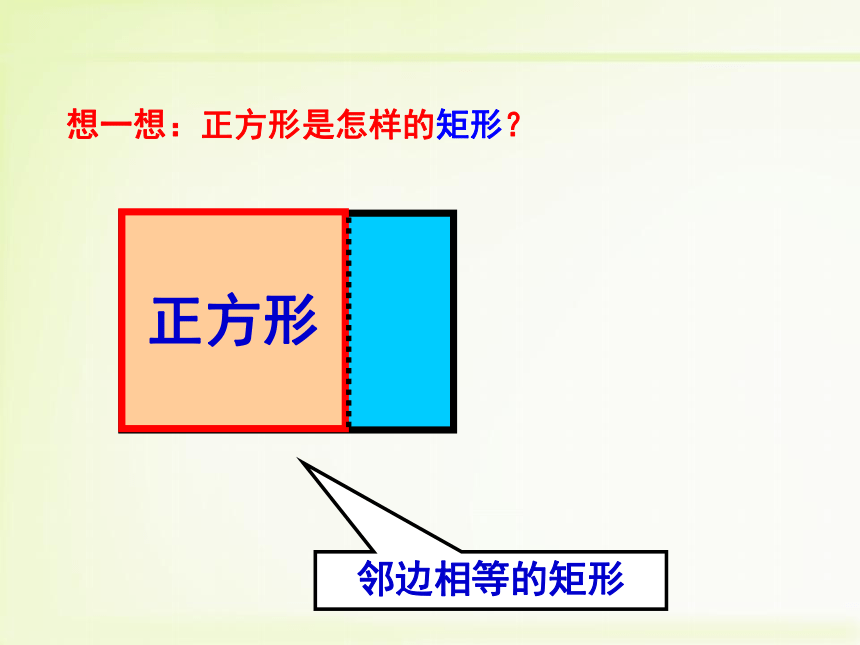
情景一★正方形是特殊的菱形1. 图中CD在平移时,这个图形始终是怎样的图形?2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?AB★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 情景二邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?菱形正方形定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形._______________的菱形是正方形. _______________的矩形是正方形.有一个角是直角有一组邻边相等轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,
两组对角相等,
对角线互相平分.(2) 具有矩形的一切性质四个角都是直角,对角线相等.(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角.(A)(B)(C)(D)1、对称性2、性质正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法 要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形? 例1 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.例2 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN证明:连接PC∵PM⊥BC , PN⊥DC 四边形ABCD是正方形∴∠NCM=90°∴四边形PMCN是矩形∴PC=MN又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=MN1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )∴ DE=DFDE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB习题18.2,第12、13题.1. 正方形是轴对称图形,有4条对称轴.
2. 正方形的四条边都相等.
3. 正方形的四个角都相等.
4. 正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角. 一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
2. 经历探索正方形有关性质和判别条件的过程,了解正方形与矩形、菱形的关系.正方形正方形有一个角是
直角
情景一★正方形是特殊的菱形1. 图中CD在平移时,这个图形始终是怎样的图形?2. 当CD移动到C?D?位置,此时AD?=AB,四边形ABCD还是矩形吗?AB★ 正方形是特殊的矩形两组互相垂直的平行线围成矩形ABCD 情景二邻边相等的矩形想一想:正方形是怎样的矩形?矩形正方形一个角是直角的菱形想一想:正方形是怎样的菱形?菱形正方形定义:一组邻边相等,并且有一个角是直角的平行四边形叫做正方形._______________的菱形是正方形. _______________的矩形是正方形.有一个角是直角有一组邻边相等轴对称图形,有4条对称轴(1)它具有平行四边形的一切性质两组对边分别平行且相等,
两组对角相等,
对角线互相平分.(2) 具有矩形的一切性质四个角都是直角,对角线相等.(3)具有菱形的一切性质四条边相等;对角线互相垂直,每条对角线平分一组对角.(A)(B)(C)(D)1、对称性2、性质正方形的判定方法:(可从平行四边形、矩形、菱形为基础)定义法 要判定一个三角形是等腰直
角三角形需要什么条件?判定两
个三角形全等的条件又是什么?
图中共有多少个等腰直角三
角形? 例1 求证:正方形的两条对角线把这个正方形分
成四个全等的等腰直角三角形.例2 如图所示,正方形ABCD中,P为BD上一点,PM⊥BC于M, PN⊥DC于N. 试说明:AP=MN证明:连接PC∵PM⊥BC , PN⊥DC 四边形ABCD是正方形∴∠NCM=90°∴四边形PMCN是矩形∴PC=MN又∵四边形BAPC是以BD为轴的轴对称图形∴AP=PC∴AP=MN1、如图,四边形ABCD是正方形,延长BC到E,使CE=AC,连接AE,交CD于F,求∠AFC的度数.2、 直角三角形ABC中,CD平分∠ACB交AB于D,DE⊥AC,DF⊥AB.求证:四边形CEDF是正方形.∴四边形ABCD是正方形(有一组邻边相等的矩形是正方形 )∴ DE=DFDE⊥AC, DF⊥BC∵ CD平分∠ACB∴ 四边形ABCD为矩形而∠ACB=90°∴ ∠DEC=90°, ∠DFC=90°证明:∵ DE⊥AC,DF⊥AB习题18.2,第12、13题.1. 正方形是轴对称图形,有4条对称轴.
2. 正方形的四条边都相等.
3. 正方形的四个角都相等.
4. 正方形的对角线互相垂直平分且相等,
且每一条对角线平分一组对角. 一组邻边相等,并且有一个角是直角的平行四边形叫做正方形.
