四川省泸州市龙马潭区2024-2025学年八年级上学期11月期中联考数学试题(含答案)
文档属性
| 名称 | 四川省泸州市龙马潭区2024-2025学年八年级上学期11月期中联考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 346.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 19:12:52 | ||
图片预览

文档简介
龙马潭区2024-2025学年上期八年级半期测试题
数 学
注意事项:
1.全卷共五个大题,25个小题;满分120分,考试时间为120分钟;
2.答题前请在答题卡上准确填写自己的学校、班级、姓名、考号;
3.考生作答时,必须将答案写在答题卡上相应的位置,在本试卷和草稿纸上答题无效,考试结束后,试题卷由学校收回并保管,答题卡交回。
一、选择题(本大题共12个小题,每小题3分,共36分;在每小题给出的四个选项中,
1.(3分)下列各选项中的两个图形属于全等形的是( )
A. B. C. D.
2.(3分)下列每组数分别是三根小木棒的长度,能摆成三角形的是( )
A.2cm,3cm,5cm B.3cm,4cm,8cm
C.1cm,1cm,3cm D.5cm,6cm,10cm
3.(3分)计算:(3a)2=( )
A.5a B.3a2 C.6a2 D.9a2
4.(3分)下列四个图形中,线段AD是△ABC的高的是( )
A.B. C.D.
5.(3分)若一个正多边形的一个外角为72°,则这个正多边形的内角和为( )
A.360° B.540° C.720° D.900°
6.(3分)如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A.SAS B.SSS C.AAS D.ASA
7.(3分)下列各式从左到右的变形中,属于因式分解的是( )
A.(x+2)=x2+4x+1 B.3a(b+c)=3ab+3ac
C.x2﹣4y2=(x+2y)(x﹣2y) D.(x﹣1)(y﹣1)=xy﹣x﹣y+1
8.(3分)若(x+2)(x﹣5)=x2+mx+n,则m,n的值分别是( )
A.m=﹣3,n=10 B.m=3,n=﹣10
C.m=3,n=10 D.m=﹣3,n=﹣10
9.(3分)如图,EF=CF,BF=DF,则下列结论错误的是( )
A.△BEF≌△DCF B.△ABC≌△ADE C.AB=AD D.DC=AC
10.(3分)如图,△ABC中,AD为中线,AB=8,AC=6,则△ABD与△ACD的周长之差为( )
A.1 B.2 C.3 D.4
11.(3分)我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A.45 B.55 C.2017 D.2018
12.(3分)如图,在△ABC中,∠A=84°,点O是∠ABC、∠ACB角平分线的交点,点P是∠BOC、∠OCB角平分线的交点,若∠P=100°,则∠ACB的度数是( )
A.42° B.60° C.56° D.65°
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(3分)如图,泸州长江六桥预计在2023年年底通车,大桥桥梁的斜拉钢索是三角形的结构,其原理是 .
14.(3分)分解因式:x3﹣4x= .
15.(3分)ax=2,ay=3,则ax+y的值为 .
16.(3分)如图,在△ABC中,AB=4,AC=6,E为BC中点,AD为△ABC的角平分线,△ABC的面积记为S1,△ADE的面积记为S2,则= .
三、本大题共3个小题,每小题6分,共18分.
17.(6分)计算:3a6b2 4ab3+36a3b4.
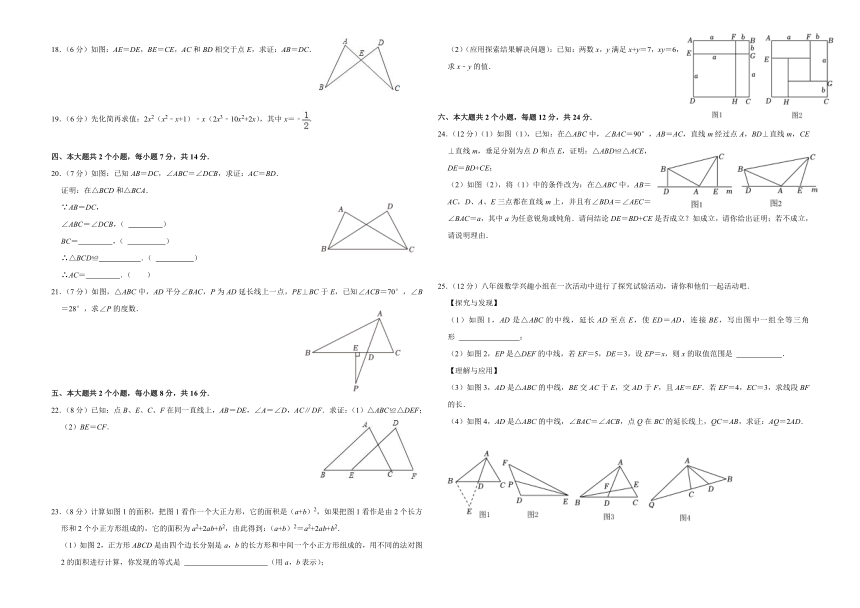
18.(6分)如图:AE=DE,BE=CE,AC和BD相交于点E,求证:AB=DC.
19.(6分)先化简再求值:2x2(x2﹣x+1)﹣x(2x3﹣10x2+2x),其中x=﹣.
四、本大题共2个小题,每小题7分,共14分.
20.(7分)如图:已知AB=DC,∠ABC=∠DCB,求证:AC=BD.
证明:在△BCD和△BCA.
∵AB=DC,
∠ABC=∠DCB,( )
BC= ,( )
∴△BCD≌ .( )
∴AC= .( )
21.(7分)如图,△ABC中,AD平分∠BAC,P为AD延长线上一点,PE⊥BC于E,已知∠ACB=70°,∠B=28°,求∠P的度数.
五、本大题共2个小题,每小题8分,共16分.
22.(8分)已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.求证:(1)△ABC≌△DEF;(2)BE=CF.
23.(8分)计算如图1的面积,把图1看作一个大正力形,它的面积是(a+b)2,如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到:(a+b)2=a2+2ab+b2.
(1)如图2,正方形ABCD是由四个边长分别是a,b的长方形和中间一个小正方形组成的,用不同的法对图2的面积进行计算,你发现的等式是 (用a,b表示);
(2)(应用探索结果解决问题):已知:两数x,y满足x+y=7,xy=6,求x﹣y的值.
六、本大题共2个小题,每题12分,共24分.
24.(12分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D和点E,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
25.(12分)八年级数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
【探究与发现】
(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中一组全等三角形 ;
(2)如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是 .
【理解与应用】
(3)如图3,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
(4)如图4,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=AB,求证:AQ=2AD.
参考答案与试题解析
一、选择题(本大题共12个小题,每小题3分,共36分;在每小题给出的四个选项中,
1.B
2.D
3.D
4.A
5.B
6.D
7.C
8.D
9.D
10.B
11.A
12.C
二、填空题(本大题共4个小题,每小题3分,共12分)
13.三角形具有稳定性.
14.x(x+2)(x﹣2).
15.6.
16.10.
三、本大题共3个小题,每小题6分,共18分.
17.12a7b5+36a3b4.
18.证明:∵AE=DE,BE=CE,∠AEB=∠CED(对顶角相等),
∴△ABE≌△DCE(SAS),
∴AB=CD.
19.解:原式=2x4﹣2x3+2x2﹣2x4+10x3﹣2x2
=8x3,
当x=﹣时,
原式=8×(﹣)3
=8×(﹣)
=﹣1.
四、本大题共2个小题,每小题7分,共14分.
20.已知,CB,公共边,△CBA,SSS,BD,全等三角形的对应边相等.
21.解:在△ABC中,∠ACB=70°,∠B=28°,
∴∠BAC=180°﹣∠ACB﹣∠B=82°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=41°.
在△ACD中,∠ACD=70°,∠CAD=41°,
∴∠ADC=180°﹣∠ACD﹣∠CAD=69°,
∴∠PDE=∠ADC=69°.
∵PE⊥BC于E,
∴∠PED=90°,
∴∠P=180°﹣∠PDE﹣∠PED=21°.
五、本大题共2个小题,每小题8分,共16分.
22.证明:(1)∵AC∥DF
∴∠ACB=∠F
在△ABC与△DEF中
,
∴△ABC≌△DEF
(2)∵△ABC≌△DEF
∴BC=EF
∴BC﹣EC=EF﹣EC
即BE=CF
23.解:(1)图2中,正方形ABCD的边长为a+b,因此面积为(a+b)2,
中间小正方形的边长为a﹣b,因此面积为(a﹣b)2,
4个长为a,宽为b的长方形的面积和为4ab,
因此有(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)得(x+y)2=(x﹣y)2+4xy,
∵x+y=7,xy=6,
∴72=(x﹣y)2+4×6,
即(x﹣y)2=49﹣24=25,
∴x﹣y=±5.
六、本大题共2个小题,每题12分,共24分.
24.证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
25.(1)解:△ADC≌△EDB,理由如下:
∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS);
故答案为:△ADC≌△EDB;
(2)解:如图2,延长EP至点Q,使PQ=PE,连接FQ,
∵EP是△DEF的中线,
∴FP=DP,
在△PDE与△PFQ中,
,
∴△PDE≌△PFQ(SAS),
∴FQ=DE=3,
在△EFQ中,EF﹣FQ<QE<EF+FQ,
即5﹣3<2x<5+3,
∴x的取值范围是:1<x<4;
故答案为:1<x<4;
(3)解:延长AD到M,使AD=DM,连接BM,如图②所示:
∵AE=EF,EF=4,EC=3
∴AC=AE+EC=4+3=7,
∵AD是△ABC中线,
∴CD=BD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC=7;
(4)证明:如图4,延长AD到M,使MD=AD,连接BM,
∴AM=2AD,
∵AD是△ABC的中线,
∴BD=CD,
在△BMD与△CAD中,
,
∴△BMD≌△CAD(SAS),
∴BM=CA,∠MBD=∠ACB,
又∠BAC=∠ACB,
∴∠ACQ=∠BAC+∠ABC=∠ACB+∠ABC=∠MBD+∠ABC=∠MBA,
在△ACQ与△MBA中,
,
∴△ACQ≌△MBA(SAS),
∴AQ=AM=2AD.
数 学
注意事项:
1.全卷共五个大题,25个小题;满分120分,考试时间为120分钟;
2.答题前请在答题卡上准确填写自己的学校、班级、姓名、考号;
3.考生作答时,必须将答案写在答题卡上相应的位置,在本试卷和草稿纸上答题无效,考试结束后,试题卷由学校收回并保管,答题卡交回。
一、选择题(本大题共12个小题,每小题3分,共36分;在每小题给出的四个选项中,
1.(3分)下列各选项中的两个图形属于全等形的是( )
A. B. C. D.
2.(3分)下列每组数分别是三根小木棒的长度,能摆成三角形的是( )
A.2cm,3cm,5cm B.3cm,4cm,8cm
C.1cm,1cm,3cm D.5cm,6cm,10cm
3.(3分)计算:(3a)2=( )
A.5a B.3a2 C.6a2 D.9a2
4.(3分)下列四个图形中,线段AD是△ABC的高的是( )
A.B. C.D.
5.(3分)若一个正多边形的一个外角为72°,则这个正多边形的内角和为( )
A.360° B.540° C.720° D.900°
6.(3分)如图,聪聪书上的三角形被墨迹污染了一部分,他根据所学知识很快画了一个与书本上完全一样的三角形,那么聪聪画图的依据是( )
A.SAS B.SSS C.AAS D.ASA
7.(3分)下列各式从左到右的变形中,属于因式分解的是( )
A.(x+2)=x2+4x+1 B.3a(b+c)=3ab+3ac
C.x2﹣4y2=(x+2y)(x﹣2y) D.(x﹣1)(y﹣1)=xy﹣x﹣y+1
8.(3分)若(x+2)(x﹣5)=x2+mx+n,则m,n的值分别是( )
A.m=﹣3,n=10 B.m=3,n=﹣10
C.m=3,n=10 D.m=﹣3,n=﹣10
9.(3分)如图,EF=CF,BF=DF,则下列结论错误的是( )
A.△BEF≌△DCF B.△ABC≌△ADE C.AB=AD D.DC=AC
10.(3分)如图,△ABC中,AD为中线,AB=8,AC=6,则△ABD与△ACD的周长之差为( )
A.1 B.2 C.3 D.4
11.(3分)我国南宋数学家杨辉所著的《详解九章算术》一书中,用如图的三角形解释二项式(a+b)n的展开式的各项系数,此三角形称为“杨辉三角”根据“杨辉三角”请计算(a+b)10的展开式中第三项的系数为( )
A.45 B.55 C.2017 D.2018
12.(3分)如图,在△ABC中,∠A=84°,点O是∠ABC、∠ACB角平分线的交点,点P是∠BOC、∠OCB角平分线的交点,若∠P=100°,则∠ACB的度数是( )
A.42° B.60° C.56° D.65°
二、填空题(本大题共4个小题,每小题3分,共12分)
13.(3分)如图,泸州长江六桥预计在2023年年底通车,大桥桥梁的斜拉钢索是三角形的结构,其原理是 .
14.(3分)分解因式:x3﹣4x= .
15.(3分)ax=2,ay=3,则ax+y的值为 .
16.(3分)如图,在△ABC中,AB=4,AC=6,E为BC中点,AD为△ABC的角平分线,△ABC的面积记为S1,△ADE的面积记为S2,则= .
三、本大题共3个小题,每小题6分,共18分.
17.(6分)计算:3a6b2 4ab3+36a3b4.
18.(6分)如图:AE=DE,BE=CE,AC和BD相交于点E,求证:AB=DC.
19.(6分)先化简再求值:2x2(x2﹣x+1)﹣x(2x3﹣10x2+2x),其中x=﹣.
四、本大题共2个小题,每小题7分,共14分.
20.(7分)如图:已知AB=DC,∠ABC=∠DCB,求证:AC=BD.
证明:在△BCD和△BCA.
∵AB=DC,
∠ABC=∠DCB,( )
BC= ,( )
∴△BCD≌ .( )
∴AC= .( )
21.(7分)如图,△ABC中,AD平分∠BAC,P为AD延长线上一点,PE⊥BC于E,已知∠ACB=70°,∠B=28°,求∠P的度数.
五、本大题共2个小题,每小题8分,共16分.
22.(8分)已知:点B、E、C、F在同一直线上,AB=DE,∠A=∠D,AC∥DF.求证:(1)△ABC≌△DEF;(2)BE=CF.
23.(8分)计算如图1的面积,把图1看作一个大正力形,它的面积是(a+b)2,如果把图1看作是由2个长方形和2个小正方形组成的,它的面积为a2+2ab+b2,由此得到:(a+b)2=a2+2ab+b2.
(1)如图2,正方形ABCD是由四个边长分别是a,b的长方形和中间一个小正方形组成的,用不同的法对图2的面积进行计算,你发现的等式是 (用a,b表示);
(2)(应用探索结果解决问题):已知:两数x,y满足x+y=7,xy=6,求x﹣y的值.
六、本大题共2个小题,每题12分,共24分.
24.(12分)(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D和点E,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
25.(12分)八年级数学兴趣小组在一次活动中进行了探究试验活动,请你和他们一起活动吧.
【探究与发现】
(1)如图1,AD是△ABC的中线,延长AD至点E,使ED=AD,连接BE,写出图中一组全等三角形 ;
(2)如图2,EP是△DEF的中线,若EF=5,DE=3,设EP=x,则x的取值范围是 .
【理解与应用】
(3)如图3,AD是△ABC的中线,BE交AC于E,交AD于F,且AE=EF.若EF=4,EC=3,求线段BF的长.
(4)如图4,AD是△ABC的中线,∠BAC=∠ACB,点Q在BC的延长线上,QC=AB,求证:AQ=2AD.
参考答案与试题解析
一、选择题(本大题共12个小题,每小题3分,共36分;在每小题给出的四个选项中,
1.B
2.D
3.D
4.A
5.B
6.D
7.C
8.D
9.D
10.B
11.A
12.C
二、填空题(本大题共4个小题,每小题3分,共12分)
13.三角形具有稳定性.
14.x(x+2)(x﹣2).
15.6.
16.10.
三、本大题共3个小题,每小题6分,共18分.
17.12a7b5+36a3b4.
18.证明:∵AE=DE,BE=CE,∠AEB=∠CED(对顶角相等),
∴△ABE≌△DCE(SAS),
∴AB=CD.
19.解:原式=2x4﹣2x3+2x2﹣2x4+10x3﹣2x2
=8x3,
当x=﹣时,
原式=8×(﹣)3
=8×(﹣)
=﹣1.
四、本大题共2个小题,每小题7分,共14分.
20.已知,CB,公共边,△CBA,SSS,BD,全等三角形的对应边相等.
21.解:在△ABC中,∠ACB=70°,∠B=28°,
∴∠BAC=180°﹣∠ACB﹣∠B=82°.
∵AD平分∠BAC,
∴∠CAD=∠BAC=41°.
在△ACD中,∠ACD=70°,∠CAD=41°,
∴∠ADC=180°﹣∠ACD﹣∠CAD=69°,
∴∠PDE=∠ADC=69°.
∵PE⊥BC于E,
∴∠PED=90°,
∴∠P=180°﹣∠PDE﹣∠PED=21°.
五、本大题共2个小题,每小题8分,共16分.
22.证明:(1)∵AC∥DF
∴∠ACB=∠F
在△ABC与△DEF中
,
∴△ABC≌△DEF
(2)∵△ABC≌△DEF
∴BC=EF
∴BC﹣EC=EF﹣EC
即BE=CF
23.解:(1)图2中,正方形ABCD的边长为a+b,因此面积为(a+b)2,
中间小正方形的边长为a﹣b,因此面积为(a﹣b)2,
4个长为a,宽为b的长方形的面积和为4ab,
因此有(a+b)2=(a﹣b)2+4ab,
故答案为:(a+b)2=(a﹣b)2+4ab;
(2)由(1)得(x+y)2=(x﹣y)2+4xy,
∵x+y=7,xy=6,
∴72=(x﹣y)2+4×6,
即(x﹣y)2=49﹣24=25,
∴x﹣y=±5.
六、本大题共2个小题,每题12分,共24分.
24.证明:(1)∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE;
(2)∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE.
25.(1)解:△ADC≌△EDB,理由如下:
∵AD是△ABC的中线,
∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS);
故答案为:△ADC≌△EDB;
(2)解:如图2,延长EP至点Q,使PQ=PE,连接FQ,
∵EP是△DEF的中线,
∴FP=DP,
在△PDE与△PFQ中,
,
∴△PDE≌△PFQ(SAS),
∴FQ=DE=3,
在△EFQ中,EF﹣FQ<QE<EF+FQ,
即5﹣3<2x<5+3,
∴x的取值范围是:1<x<4;
故答案为:1<x<4;
(3)解:延长AD到M,使AD=DM,连接BM,如图②所示:
∵AE=EF,EF=4,EC=3
∴AC=AE+EC=4+3=7,
∵AD是△ABC中线,
∴CD=BD,
在△ADC和△MDB中,
,
∴△ADC≌△MDB(SAS),
∴BM=AC,∠CAD=∠M,
∵AE=EF,
∴∠CAD=∠AFE,
∵∠AFE=∠BFD,
∴∠BFD=∠CAD=∠M,
∴BF=BM=AC=7;
(4)证明:如图4,延长AD到M,使MD=AD,连接BM,
∴AM=2AD,
∵AD是△ABC的中线,
∴BD=CD,
在△BMD与△CAD中,
,
∴△BMD≌△CAD(SAS),
∴BM=CA,∠MBD=∠ACB,
又∠BAC=∠ACB,
∴∠ACQ=∠BAC+∠ABC=∠ACB+∠ABC=∠MBD+∠ABC=∠MBA,
在△ACQ与△MBA中,
,
∴△ACQ≌△MBA(SAS),
∴AQ=AM=2AD.
同课章节目录
