人教版八年级数学下册18.2.1矩形(第1课时)课件(15张ppt)
文档属性
| 名称 | 人教版八年级数学下册18.2.1矩形(第1课时)课件(15张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 00:00:00 | ||
图片预览



文档简介
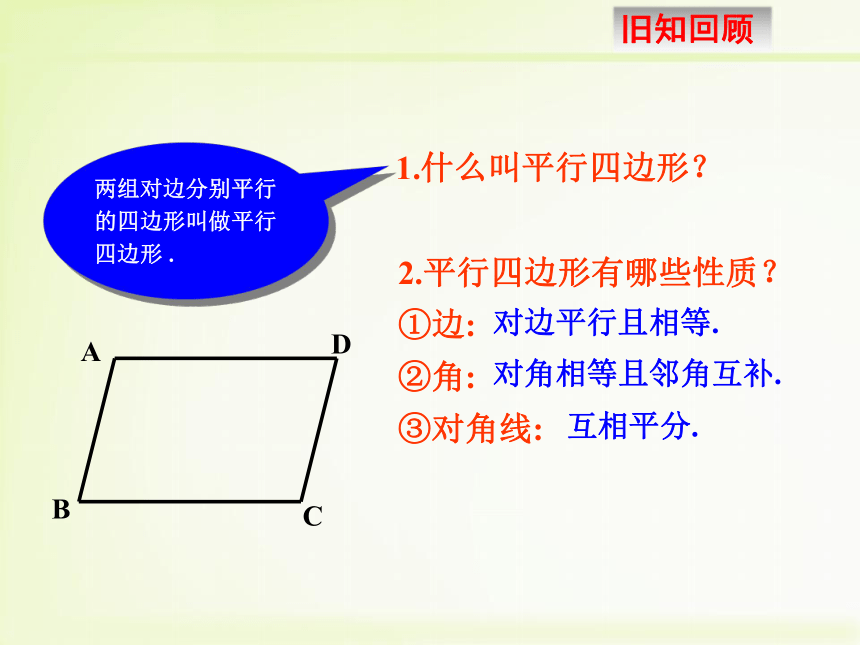
课件15张PPT。18.2.1 矩形(第1课时)第十八章 平行四边形 —矩形的定义性质及推论1.什么叫平行四边形?2.平行四边形有哪些性质?
①边:
②角:
③对角线:两组对边分别平行的四边形叫做平行四边形 .对边平行且相等.对角相等且邻角互补.互相平分.1. 理解矩形的概念,明确矩形与平行四边形之间的关系;
2. 探索并能够证明矩形的性质定理;
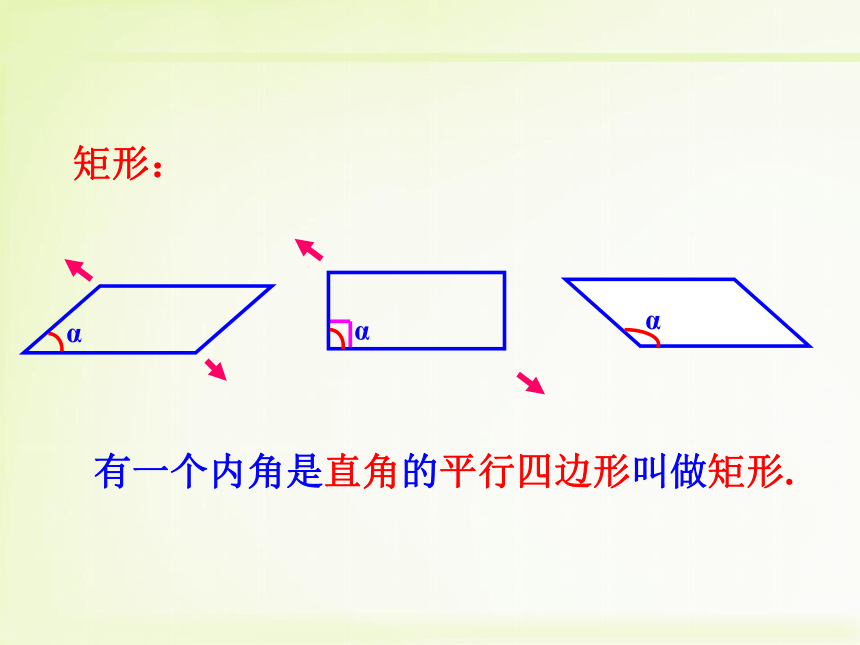
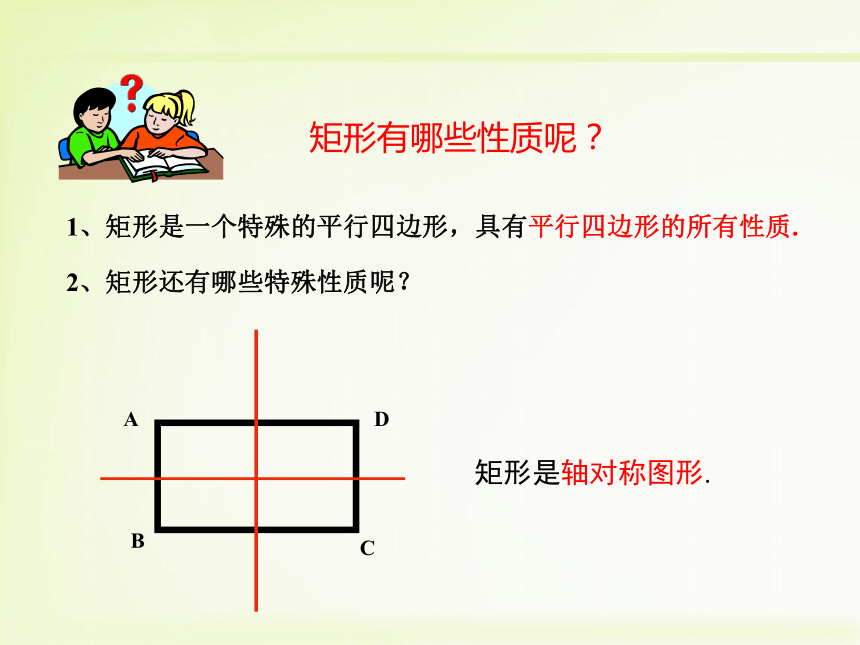
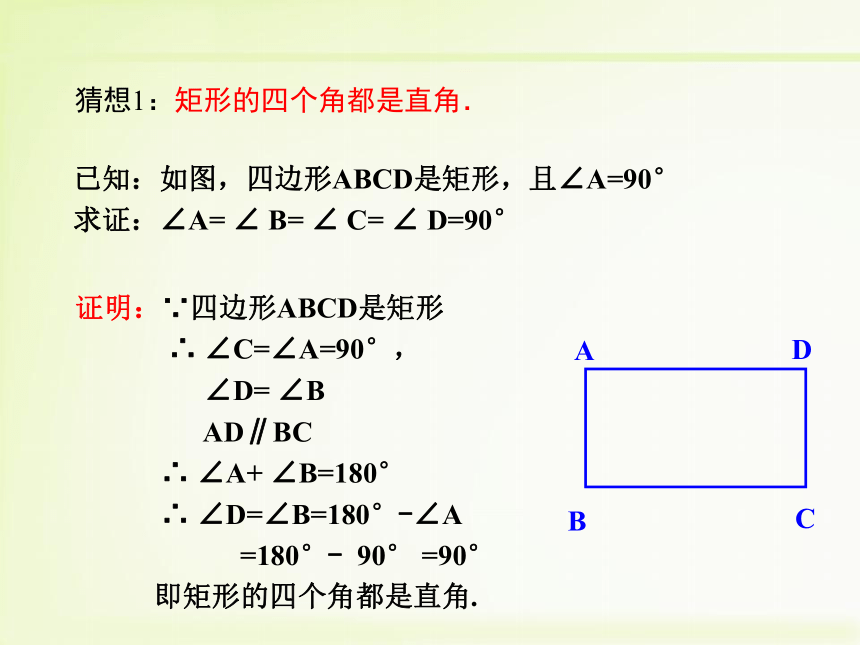
3. 探索并证明性质定理:直角三角形斜边的中线等于斜边的一半.阅读课文第52页到第53页,思考以下问题:1、什么叫矩形?2、矩形有哪些性质定理和推论?矩形:有一个内角是直角的平行四边形叫做矩形.1、矩形是一个特殊的平行四边形,具有平行四边形的所有性质.矩形有哪些性质呢?ABCD矩形是轴对称图形.2、矩形还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.证明:∵四边形ABCD是矩形
∴ ∠C=∠A=90°,
∠D= ∠B
AD∥BC
∴ ∠A+ ∠B=180°
∴ ∠D=∠B=180°-∠A
=180°- 90° =90°
即矩形的四个角都是直角.已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A= ∠ B= ∠ C= ∠ D=90° 猜想2:矩形的对角线相等.已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD即矩形的对角线相等.矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°数学语言∵四边形ABCD是矩形 ∴AC = BDOD证明: 延长BO至D, 使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=90°∴平行四边形ABCD是矩形∴AC=BD直角三角形的性质定理2
直角三角形斜边上的中线等于斜边的一半. O 例1 如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm. 求AC的长.解:1、判断下列命题是否是真命题?
(1)平行四边形的两条对角线的长度相等
(2)矩形相邻的两个角的度数相等
(3)矩形的两条对角线互相平分
(4)矩形的对角线平分它的一组对角假命题真命题真命题假命题2、已知: 如图, 过矩形ABCD的顶点作CE//BD,
交AB的延长线于E. 求证:∠CAE=∠CEA※ 矩形的性质定理1矩形的四个角都是直角.※ 矩形的性质定理2矩形的对角线相等.※ 直角三角形的性质定理2 直角三角形斜边上的中线等于斜边的一半.矩形是轴对称图形,两条对称轴.教材P53,练习第2题.
①边:
②角:
③对角线:两组对边分别平行的四边形叫做平行四边形 .对边平行且相等.对角相等且邻角互补.互相平分.1. 理解矩形的概念,明确矩形与平行四边形之间的关系;
2. 探索并能够证明矩形的性质定理;
3. 探索并证明性质定理:直角三角形斜边的中线等于斜边的一半.阅读课文第52页到第53页,思考以下问题:1、什么叫矩形?2、矩形有哪些性质定理和推论?矩形:有一个内角是直角的平行四边形叫做矩形.1、矩形是一个特殊的平行四边形,具有平行四边形的所有性质.矩形有哪些性质呢?ABCD矩形是轴对称图形.2、矩形还有哪些特殊性质呢?猜想1:矩形的四个角都是直角.证明:∵四边形ABCD是矩形
∴ ∠C=∠A=90°,
∠D= ∠B
AD∥BC
∴ ∠A+ ∠B=180°
∴ ∠D=∠B=180°-∠A
=180°- 90° =90°
即矩形的四个角都是直角.已知:如图,四边形ABCD是矩形,且∠A=90°
求证:∠A= ∠ B= ∠ C= ∠ D=90° 猜想2:矩形的对角线相等.已知:四边形ABCD是矩形
求证:AC = BD证明:在矩形ABCD中∵∠ABC = ∠DCB = 90°又∵AB = DC , BC = CB∴△ABC≌△DCB∴AC = BD即矩形的对角线相等.矩形的四个角都是直角.矩形的两条对角线相等.从角上看:从对角线上看:数学语言∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=90°数学语言∵四边形ABCD是矩形 ∴AC = BDOD证明: 延长BO至D, 使OD=BO,
连结AD、DC.∵AO=OC, BO=OD
∴四边形ABCD是平行四边形. ∵∠ABC=90°∴平行四边形ABCD是矩形∴AC=BD直角三角形的性质定理2
直角三角形斜边上的中线等于斜边的一半. O 例1 如图,矩形ABCD的两条对角线相交于点O,
已知∠BOC=120°,AB=6cm. 求AC的长.解:1、判断下列命题是否是真命题?
(1)平行四边形的两条对角线的长度相等
(2)矩形相邻的两个角的度数相等
(3)矩形的两条对角线互相平分
(4)矩形的对角线平分它的一组对角假命题真命题真命题假命题2、已知: 如图, 过矩形ABCD的顶点作CE//BD,
交AB的延长线于E. 求证:∠CAE=∠CEA※ 矩形的性质定理1矩形的四个角都是直角.※ 矩形的性质定理2矩形的对角线相等.※ 直角三角形的性质定理2 直角三角形斜边上的中线等于斜边的一半.矩形是轴对称图形,两条对称轴.教材P53,练习第2题.
