第13章 轴对称 章末检测卷(含详解)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第13章 轴对称 章末检测卷(含详解)2024-2025学年人教版数学八年级上册 |  | |
| 格式 | docx | ||
| 文件大小 | 355.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 20:33:50 | ||
图片预览



文档简介
第13章轴对称章末检测卷-2024-2025学年数学八年级上册人教版
一.选择题(共8小题)
1.(2024 滨海新区校级模拟)如图所示的两位数中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(2024秋 柳南区校级期中)如果一个等腰三角形的两边长分别为4cm和3cm,那么它的周长是( )
A.10cm B.11cm
C.10cm或11cm D.以上答案都不对.
3.(2024秋 海淀区校级期中)在平面直角坐标系中,线段AB两端点的坐标分别为A(﹣1,2)、B(2,﹣3).作AB关于某直线的对称图形A′B′,若B′的坐标为(﹣2,﹣3),则A′的坐标为( )
A.(1,2) B.(2,1) C.(1,﹣2) D.(﹣1,﹣2)
4.(2024秋 南京期中)桌面上有A,B两个球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示4个点中,可以瞄准的点是( )
A.D B.E C.F D.G
5.(2024秋 武威期中)若点P为△ABC内部一点,且PA=PB=PC,则点P是△ABC的( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
6.(2024秋 定陶区校级期中)如图,在△ABC中,∠A=105°,AC的垂直平分线l交BC于点M,AB+BM=BC,则∠B的度数为( )
A.45° B.50° C.55° D.60°
7.(2024秋 海淀区校级期中)如图,在△ABC中,∠ABC=60°,AD⊥BC于D点,AB=12,.若点E、F分别是线段AD、线段AB上的动点,则BE+EF的最小值是( )
A.6 B.12 C. D.
8.(2024春 肇源县期末)已知:如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E.若∠BAC=104°,则∠DAE的度数为( )
A.22° B.24° C.26° D.28°
二.填空题(共8小题)
9.(2024秋 同安区期中)在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是 .
10.(2023秋 哈密市期末)等腰三角形的一个角是50°,则它的顶角的度数是 .
11.(2024秋 同安区期中)在△ABC中,AB=AC,AB>BC,DE垂直平分AC,分别交AB,AC于点D,E,连接CD.若AC=4,CD=3,则BD的长为 .
12.(2024秋 新邵县期中)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 cm.
13.(2024秋 松原期中)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD相交构成的锐角为 度.
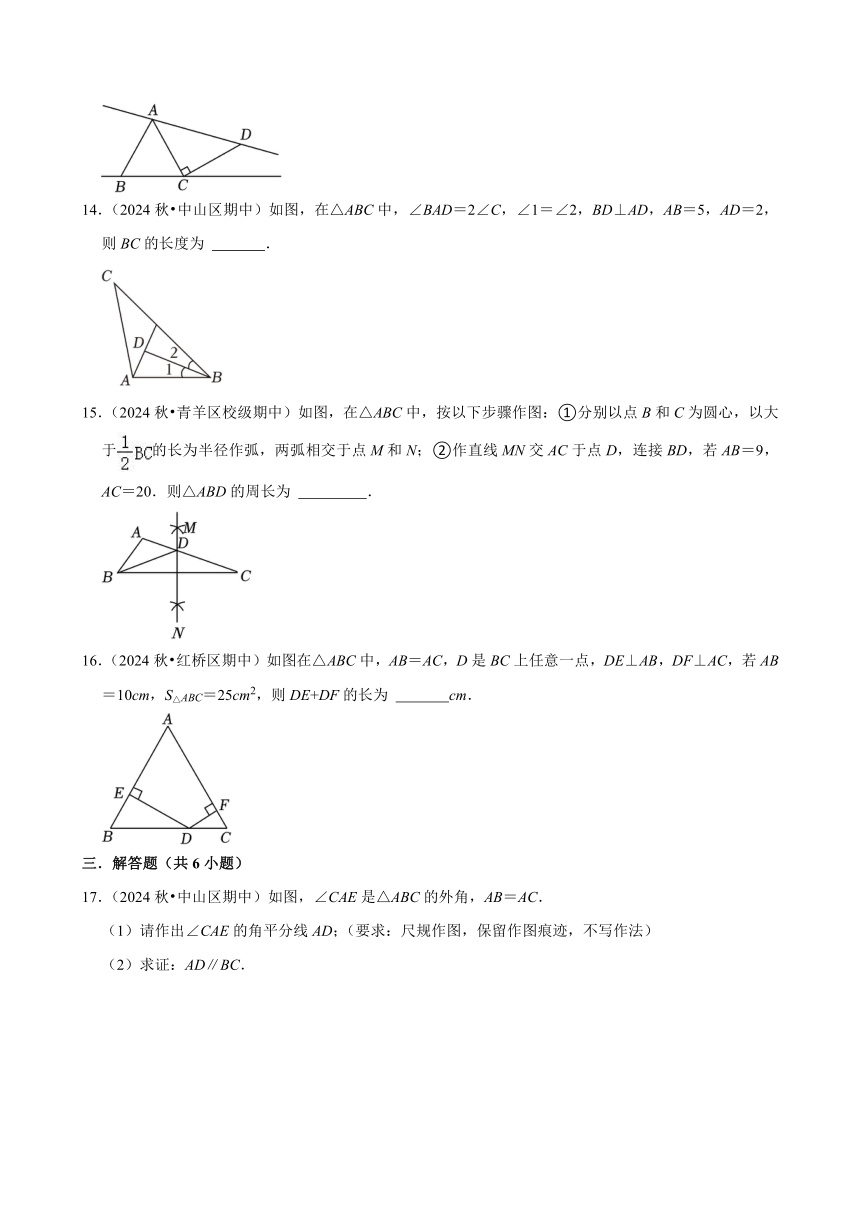
14.(2024秋 中山区期中)如图,在△ABC中,∠BAD=2∠C,∠1=∠2,BD⊥AD,AB=5,AD=2,则BC的长度为 .
15.(2024秋 青羊区校级期中)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD,若AB=9,AC=20.则△ABD的周长为 .
16.(2024秋 红桥区期中)如图在△ABC中,AB=AC,D是BC上任意一点,DE⊥AB,DF⊥AC,若AB=10cm,S△ABC=25cm2,则DE+DF的长为 cm.
三.解答题(共6小题)
17.(2024秋 中山区期中)如图,∠CAE是△ABC的外角,AB=AC.
(1)请作出∠CAE的角平分线AD;(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:AD∥BC.
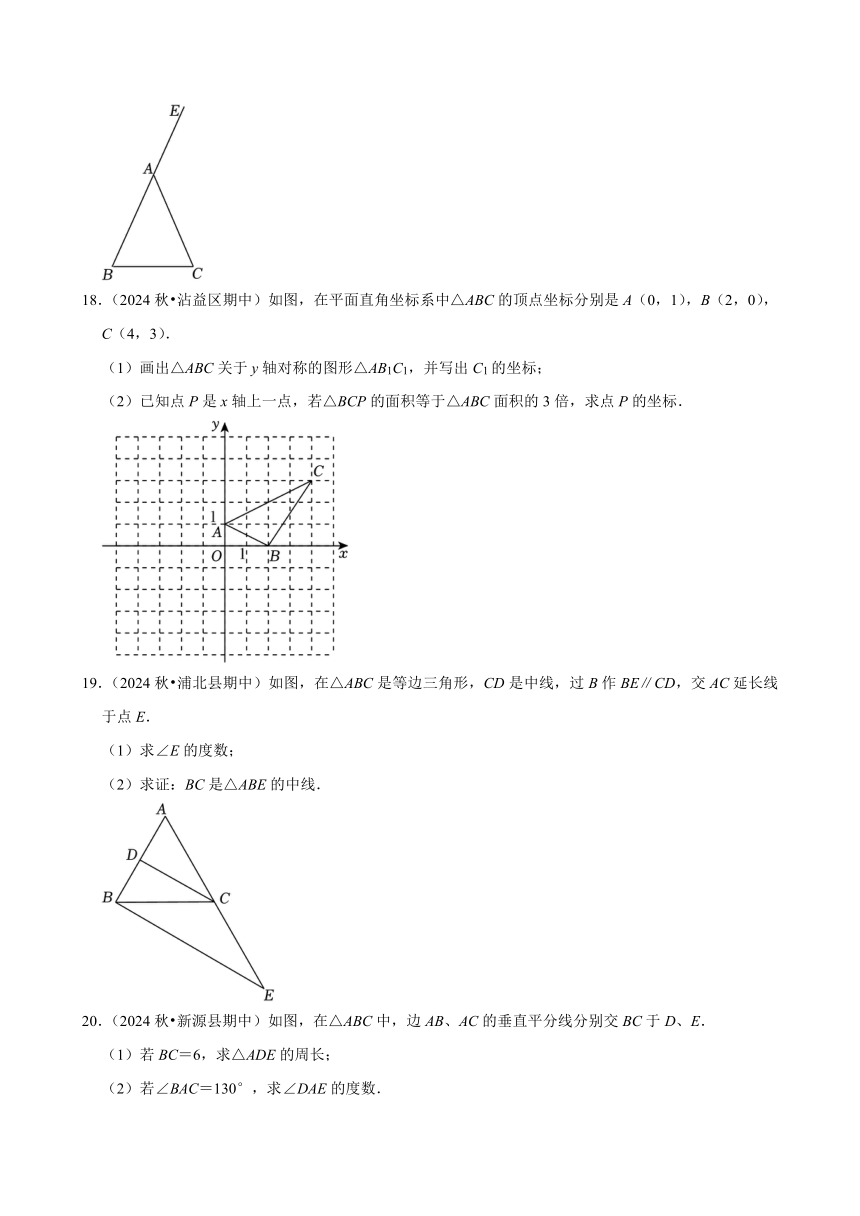
18.(2024秋 沾益区期中)如图,在平面直角坐标系中△ABC的顶点坐标分别是A(0,1),B(2,0),C(4,3).
(1)画出△ABC关于y轴对称的图形△AB1C1,并写出C1的坐标;
(2)已知点P是x轴上一点,若△BCP的面积等于△ABC面积的3倍,求点P的坐标.
19.(2024秋 浦北县期中)如图,在△ABC是等边三角形,CD是中线,过B作BE∥CD,交AC延长线于点E.
(1)求∠E的度数;
(2)求证:BC是△ABE的中线.
20.(2024秋 新源县期中)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
21.(2024春 丰城市校级期末)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
22.(2024秋 宜兴市月考)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长;
(2)若∠ABC=30°,∠C=45°,求∠EAC的度数.
第13章轴对称章末检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024 滨海新区校级模拟)如图所示的两位数中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:第一个不是轴对称图形;
第二个是轴对称图形;
第三个不是轴对称图形;
第四个是轴对称图形;
故选:B.
2.(2024秋 柳南区校级期中)如果一个等腰三角形的两边长分别为4cm和3cm,那么它的周长是( )
A.10cm B.11cm
C.10cm或11cm D.以上答案都不对.
【解答】解:(1)当4cm是底边时,3+3>4,能构成三角形,周长=4+3+3=10(cm);
(2)当3cm是底边时,4+4>3,可以构成三角形,周长=4+4+3=11(cm).
故选:C.
3.(2024秋 海淀区校级期中)在平面直角坐标系中,线段AB两端点的坐标分别为A(﹣1,2)、B(2,﹣3).作AB关于某直线的对称图形A′B′,若B′的坐标为(﹣2,﹣3),则A′的坐标为( )
A.(1,2) B.(2,1) C.(1,﹣2) D.(﹣1,﹣2)
【解答】解:如图,
∵B(2,﹣3),B′(﹣2,﹣3),
∴点B与点B'关于y轴对称,
即线段AB与线段A′B′关于y轴对称,
∴A′的坐标为(1,2).
故选:A.
4.(2024秋 南京期中)桌面上有A,B两个球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示4个点中,可以瞄准的点是( )
A.D B.E C.F D.G
【解答】解:根据题中所给的信息进行判断可得:将B球射向桌面的点D,可使一次反弹后击中A球,
故选:A.
5.(2024秋 武威期中)若点P为△ABC内部一点,且PA=PB=PC,则点P是△ABC的( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
【解答】解:三角形的三边垂直平分线的交点的性质为:到三角形三个顶点的距离.
故选:D.
6.(2024秋 定陶区校级期中)如图,在△ABC中,∠A=105°,AC的垂直平分线l交BC于点M,AB+BM=BC,则∠B的度数为( )
A.45° B.50° C.55° D.60°
【解答】解:如图,连接AM,
∵AC的垂直平分线l交BC于点M,
∴CM=AM,
∵AB+BM=BC,CM+BM=BC,
∴AB=CM=AM,
∴∠C=∠MAC,∠AMB=∠B,
设∠C=∠MAC=x,则∠AMB=∠B=2x,
∴∠BAM=180°﹣4x,
∵∠BAC=∠MAC+∠BAM=x+180°﹣4x=105°,
∴x=25°,
∴∠B=2x=50°,
故选:B.
7.(2024秋 海淀区校级期中)如图,在△ABC中,∠ABC=60°,AD⊥BC于D点,AB=12,.若点E、F分别是线段AD、线段AB上的动点,则BE+EF的最小值是( )
A.6 B.12 C. D.
【解答】解:∵AD⊥BC,
∴∠ADB=90°,
如图,作点B关于AD的对称点B',过点B'作B'F⊥AB于F,交AD于E,
∴AD是BB'的垂直平分线,
∴BE=B'E,
此时BE+EF的值最小,其最小值是B'F,
∵∠ABC=60°,∠ADB=90°,
∴∠BAD=30°,
∴BD=AB=×12=6,
∴BB'=12=AB,
∵∠ABD=∠FBB',∠ADB=∠BFB'=90°,
∴AD=B'F=6,
即BE+EF的最小值是6;
故选:C.
8.(2024春 肇源县期末)已知:如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E.若∠BAC=104°,则∠DAE的度数为( )
A.22° B.24° C.26° D.28°
【解答】解:∵∠BAC=104°,
∴∠B+∠C=180°﹣∠BAC=76°,
∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=76°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=104°﹣76°=28°,
故选:D.
二.填空题(共8小题)
9.(2024秋 同安区期中)在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是 (﹣3,2) .
【解答】解:在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是(﹣3,2).
故答案为:(﹣3,2).
10.(2023秋 哈密市期末)等腰三角形的一个角是50°,则它的顶角的度数是 50°或80° .
【解答】解:①当50°角为顶角时,顶角度数为50°;
②当50°为底角时,顶角=180°﹣2×50°=80°,
故答案为:50°或80°.
11.(2024秋 同安区期中)在△ABC中,AB=AC,AB>BC,DE垂直平分AC,分别交AB,AC于点D,E,连接CD.若AC=4,CD=3,则BD的长为 1 .
【解答】解:如图,
∵DE垂直平分AC,CD=3,
∴AD=CD=3,
∵AB=AC=4,
∴BD=AB﹣AD=1,
故答案为:1.
12.(2024秋 新邵县期中)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 8 cm.
【解答】解:∵DE垂直平分AB,
∴BD=AD,
∵△DBC的周长=BD+CD+BC=18cm,
∴CD+BC+AD=18cm,
∵AB=AC=AD+DC=10cm,
∴BC=18﹣10=8(cm),
故答案为:8.
13.(2024秋 松原期中)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD相交构成的锐角为 15 度.
【解答】解:延长AD与BC交于点E,如图所示:
∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
又∵△ACD为等腰直角三角形,AC=CD,
∴∠CAD=45°,
∴∠BAD=∠BAC+∠CAD=60°+45°=105°,
∴∠E=180°﹣(∠ABC+∠BAD)=180°﹣(60°+105°)=15°.
即直线BC与直线AD的夹角为15°.
故答案为:15.
14.(2024秋 中山区期中)如图,在△ABC中,∠BAD=2∠C,∠1=∠2,BD⊥AD,AB=5,AD=2,则BC的长度为 9 .
【解答】解:如图,在△ABE中,AD⊥BD,∠1=∠2,
∴AD=DE=2,AB=BE=5,
∴∠BAD=∠BED
又∵∠BED=∠C+∠CAE,∠BAD=2∠C,
∴∠C=∠CAE,
∴CE=AE=2AD=4,
∴BC=BE+CE=5+4=9.
故答案为:9.
15.(2024秋 青羊区校级期中)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD,若AB=9,AC=20.则△ABD的周长为 29 .
【解答】解:由作图过程可知,直线MN为线段BC的垂直平分线,
∴BD=CD,
∴△ABD的周长为AB+AD+BD=AB+AD+CD=AB+AC=9+20=29.
故答案为:29.
16.(2024秋 红桥区期中)如图在△ABC中,AB=AC,D是BC上任意一点,DE⊥AB,DF⊥AC,若AB=10cm,S△ABC=25cm2,则DE+DF的长为 5 cm.
【解答】解:如图,连接AD,
∵AB=AC,DE⊥AB,DF⊥AC,
∴S△ABC=S△ABD+S△ADC=AB DE+AC DF=AB(DE+DF),
∵AB=10cm,S△ABC=25cm2,
∴,
解得:DE+DF=5(cm),
故答案为:5.
三.解答题(共6小题)
17.(2024秋 中山区期中)如图,∠CAE是△ABC的外角,AB=AC.
(1)请作出∠CAE的角平分线AD;(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:AD∥BC.
【解答】(1)解:如图,射线AD即为所求.
(2)证明:∵AB=AC,
∴∠B=∠C,
∴∠EAC=∠B+∠C=2∠B.
∵AD为∠EAC的平分线,
∴∠EAD=∠CAD,
∴∠EAC=2∠EAD,
∴∠EAD=∠B,
∴AD∥BC.
18.(2024秋 沾益区期中)如图,在平面直角坐标系中△ABC的顶点坐标分别是A(0,1),B(2,0),C(4,3).
(1)画出△ABC关于y轴对称的图形△AB1C1,并写出C1的坐标;
(2)已知点P是x轴上一点,若△BCP的面积等于△ABC面积的3倍,求点P的坐标.
【解答】解:(1)如图,△AB1C1即为所求.
由图可得,C1的坐标为(﹣4,3).
(2)△ABC的面积为=8﹣1﹣3=4.
设点P的坐标为(m,0),
∵△BCP的面积等于△ABC面积的3倍,
∴,
解得m=﹣6或10,
∴点P的坐标为(﹣6,0)或(10,0).
19.(2024秋 浦北县期中)如图,在△ABC是等边三角形,CD是中线,过B作BE∥CD,交AC延长线于点E.
(1)求∠E的度数;
(2)求证:BC是△ABE的中线.
【解答】(1)解:∵△ABC是等边三角形,CD是中线,
∴CD平分∠ACB,
∴,
∵BE∥CD,
∴∠ACD=∠E=30°;
(2)证明:由(1)可知,∠BCD=30°,∠E=30°,
∵BE∥CD,
∴∠BCD=∠CBE=30°,
∴∠CBE=∠E,
∴BC=CE,
∵在等边△ABC中,AC=BC,
∴AC=CE,
∴BC是△ABE的中线.
20.(2024秋 新源县期中)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
【解答】解:(1)在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6;
(2)∵∠BAC=130°,
∴∠B+∠C=50°,
∵DA=DB,EA=EC,
∴∠BAD=∠B,∠EAC=∠C,
∴∠BAD+∠EAC=50°,
∴∠DAE=∠BAC﹣(∠BAD+∠EAC)=130°﹣50°=80°.
21.(2024春 丰城市校级期末)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
【解答】解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为19,△DEC的周长为7,
∴AB+BE+CE+CD+AD=19,CD+EC+DE=CD+CE+AD=7,
∴AB+BE=19﹣7=12,
∴AB=BE=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
22.(2024秋 宜兴市月考)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长;
(2)若∠ABC=30°,∠C=45°,求∠EAC的度数.
【解答】解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为19,△DEC的周长为7,
∴AB+BE+CE+CD+AD=19,CD+EC+DE=CD+CE+AD=7,
∴AB+BE=19﹣7=12,
∴AB=BE=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
∵AB=BE,
∴,
∴∠EAC=∠BAC﹣∠BAE=30°.
一.选择题(共8小题)
1.(2024 滨海新区校级模拟)如图所示的两位数中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
2.(2024秋 柳南区校级期中)如果一个等腰三角形的两边长分别为4cm和3cm,那么它的周长是( )
A.10cm B.11cm
C.10cm或11cm D.以上答案都不对.
3.(2024秋 海淀区校级期中)在平面直角坐标系中,线段AB两端点的坐标分别为A(﹣1,2)、B(2,﹣3).作AB关于某直线的对称图形A′B′,若B′的坐标为(﹣2,﹣3),则A′的坐标为( )
A.(1,2) B.(2,1) C.(1,﹣2) D.(﹣1,﹣2)
4.(2024秋 南京期中)桌面上有A,B两个球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示4个点中,可以瞄准的点是( )
A.D B.E C.F D.G
5.(2024秋 武威期中)若点P为△ABC内部一点,且PA=PB=PC,则点P是△ABC的( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
6.(2024秋 定陶区校级期中)如图,在△ABC中,∠A=105°,AC的垂直平分线l交BC于点M,AB+BM=BC,则∠B的度数为( )
A.45° B.50° C.55° D.60°
7.(2024秋 海淀区校级期中)如图,在△ABC中,∠ABC=60°,AD⊥BC于D点,AB=12,.若点E、F分别是线段AD、线段AB上的动点,则BE+EF的最小值是( )
A.6 B.12 C. D.
8.(2024春 肇源县期末)已知:如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E.若∠BAC=104°,则∠DAE的度数为( )
A.22° B.24° C.26° D.28°
二.填空题(共8小题)
9.(2024秋 同安区期中)在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是 .
10.(2023秋 哈密市期末)等腰三角形的一个角是50°,则它的顶角的度数是 .
11.(2024秋 同安区期中)在△ABC中,AB=AC,AB>BC,DE垂直平分AC,分别交AB,AC于点D,E,连接CD.若AC=4,CD=3,则BD的长为 .
12.(2024秋 新邵县期中)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 cm.
13.(2024秋 松原期中)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD相交构成的锐角为 度.
14.(2024秋 中山区期中)如图,在△ABC中,∠BAD=2∠C,∠1=∠2,BD⊥AD,AB=5,AD=2,则BC的长度为 .
15.(2024秋 青羊区校级期中)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD,若AB=9,AC=20.则△ABD的周长为 .
16.(2024秋 红桥区期中)如图在△ABC中,AB=AC,D是BC上任意一点,DE⊥AB,DF⊥AC,若AB=10cm,S△ABC=25cm2,则DE+DF的长为 cm.
三.解答题(共6小题)
17.(2024秋 中山区期中)如图,∠CAE是△ABC的外角,AB=AC.
(1)请作出∠CAE的角平分线AD;(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:AD∥BC.
18.(2024秋 沾益区期中)如图,在平面直角坐标系中△ABC的顶点坐标分别是A(0,1),B(2,0),C(4,3).
(1)画出△ABC关于y轴对称的图形△AB1C1,并写出C1的坐标;
(2)已知点P是x轴上一点,若△BCP的面积等于△ABC面积的3倍,求点P的坐标.
19.(2024秋 浦北县期中)如图,在△ABC是等边三角形,CD是中线,过B作BE∥CD,交AC延长线于点E.
(1)求∠E的度数;
(2)求证:BC是△ABE的中线.
20.(2024秋 新源县期中)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
21.(2024春 丰城市校级期末)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
22.(2024秋 宜兴市月考)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长;
(2)若∠ABC=30°,∠C=45°,求∠EAC的度数.
第13章轴对称章末检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024 滨海新区校级模拟)如图所示的两位数中,是轴对称图形的有( )
A.1个 B.2个 C.3个 D.4个
【解答】解:第一个不是轴对称图形;
第二个是轴对称图形;
第三个不是轴对称图形;
第四个是轴对称图形;
故选:B.
2.(2024秋 柳南区校级期中)如果一个等腰三角形的两边长分别为4cm和3cm,那么它的周长是( )
A.10cm B.11cm
C.10cm或11cm D.以上答案都不对.
【解答】解:(1)当4cm是底边时,3+3>4,能构成三角形,周长=4+3+3=10(cm);
(2)当3cm是底边时,4+4>3,可以构成三角形,周长=4+4+3=11(cm).
故选:C.
3.(2024秋 海淀区校级期中)在平面直角坐标系中,线段AB两端点的坐标分别为A(﹣1,2)、B(2,﹣3).作AB关于某直线的对称图形A′B′,若B′的坐标为(﹣2,﹣3),则A′的坐标为( )
A.(1,2) B.(2,1) C.(1,﹣2) D.(﹣1,﹣2)
【解答】解:如图,
∵B(2,﹣3),B′(﹣2,﹣3),
∴点B与点B'关于y轴对称,
即线段AB与线段A′B′关于y轴对称,
∴A′的坐标为(1,2).
故选:A.
4.(2024秋 南京期中)桌面上有A,B两个球,若要将B球射向桌面任意一边,使一次反弹后击中A球,则如图所示4个点中,可以瞄准的点是( )
A.D B.E C.F D.G
【解答】解:根据题中所给的信息进行判断可得:将B球射向桌面的点D,可使一次反弹后击中A球,
故选:A.
5.(2024秋 武威期中)若点P为△ABC内部一点,且PA=PB=PC,则点P是△ABC的( )
A.三条中线的交点
B.三条内角平分线的交点
C.三条高的交点
D.三条边的垂直平分线的交点
【解答】解:三角形的三边垂直平分线的交点的性质为:到三角形三个顶点的距离.
故选:D.
6.(2024秋 定陶区校级期中)如图,在△ABC中,∠A=105°,AC的垂直平分线l交BC于点M,AB+BM=BC,则∠B的度数为( )
A.45° B.50° C.55° D.60°
【解答】解:如图,连接AM,
∵AC的垂直平分线l交BC于点M,
∴CM=AM,
∵AB+BM=BC,CM+BM=BC,
∴AB=CM=AM,
∴∠C=∠MAC,∠AMB=∠B,
设∠C=∠MAC=x,则∠AMB=∠B=2x,
∴∠BAM=180°﹣4x,
∵∠BAC=∠MAC+∠BAM=x+180°﹣4x=105°,
∴x=25°,
∴∠B=2x=50°,
故选:B.
7.(2024秋 海淀区校级期中)如图,在△ABC中,∠ABC=60°,AD⊥BC于D点,AB=12,.若点E、F分别是线段AD、线段AB上的动点,则BE+EF的最小值是( )
A.6 B.12 C. D.
【解答】解:∵AD⊥BC,
∴∠ADB=90°,
如图,作点B关于AD的对称点B',过点B'作B'F⊥AB于F,交AD于E,
∴AD是BB'的垂直平分线,
∴BE=B'E,
此时BE+EF的值最小,其最小值是B'F,
∵∠ABC=60°,∠ADB=90°,
∴∠BAD=30°,
∴BD=AB=×12=6,
∴BB'=12=AB,
∵∠ABD=∠FBB',∠ADB=∠BFB'=90°,
∴AD=B'F=6,
即BE+EF的最小值是6;
故选:C.
8.(2024春 肇源县期末)已知:如图,在△ABC中,AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E.若∠BAC=104°,则∠DAE的度数为( )
A.22° B.24° C.26° D.28°
【解答】解:∵∠BAC=104°,
∴∠B+∠C=180°﹣∠BAC=76°,
∵AB的垂直平分线交BC于点D,AC的垂直平分线交BC于点E,
∴DA=DB,EA=EC,
∴∠DAB=∠B,∠EAC=∠C,
∴∠DAB+∠EAC=∠B+∠C=76°,
∴∠DAE=∠BAC﹣(∠DAB+∠EAC)=104°﹣76°=28°,
故选:D.
二.填空题(共8小题)
9.(2024秋 同安区期中)在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是 (﹣3,2) .
【解答】解:在平面直角坐标系中,点(﹣3,﹣2)关于x轴对称的点的坐标是(﹣3,2).
故答案为:(﹣3,2).
10.(2023秋 哈密市期末)等腰三角形的一个角是50°,则它的顶角的度数是 50°或80° .
【解答】解:①当50°角为顶角时,顶角度数为50°;
②当50°为底角时,顶角=180°﹣2×50°=80°,
故答案为:50°或80°.
11.(2024秋 同安区期中)在△ABC中,AB=AC,AB>BC,DE垂直平分AC,分别交AB,AC于点D,E,连接CD.若AC=4,CD=3,则BD的长为 1 .
【解答】解:如图,
∵DE垂直平分AC,CD=3,
∴AD=CD=3,
∵AB=AC=4,
∴BD=AB﹣AD=1,
故答案为:1.
12.(2024秋 新邵县期中)如图,在△ABC中,AB=AC=10cm,DE垂直平分AB,垂足为E,交AC于D,若△DBC的周长为18cm,则BC的长为 8 cm.
【解答】解:∵DE垂直平分AB,
∴BD=AD,
∵△DBC的周长=BD+CD+BC=18cm,
∴CD+BC+AD=18cm,
∵AB=AC=AD+DC=10cm,
∴BC=18﹣10=8(cm),
故答案为:8.
13.(2024秋 松原期中)如图,△ABC为等边三角形,△ACD为等腰直角三角形,AC=CD,则直线BC与直线AD相交构成的锐角为 15 度.
【解答】解:延长AD与BC交于点E,如图所示:
∵△ABC为等边三角形,
∴∠ABC=∠BAC=60°,
又∵△ACD为等腰直角三角形,AC=CD,
∴∠CAD=45°,
∴∠BAD=∠BAC+∠CAD=60°+45°=105°,
∴∠E=180°﹣(∠ABC+∠BAD)=180°﹣(60°+105°)=15°.
即直线BC与直线AD的夹角为15°.
故答案为:15.
14.(2024秋 中山区期中)如图,在△ABC中,∠BAD=2∠C,∠1=∠2,BD⊥AD,AB=5,AD=2,则BC的长度为 9 .
【解答】解:如图,在△ABE中,AD⊥BD,∠1=∠2,
∴AD=DE=2,AB=BE=5,
∴∠BAD=∠BED
又∵∠BED=∠C+∠CAE,∠BAD=2∠C,
∴∠C=∠CAE,
∴CE=AE=2AD=4,
∴BC=BE+CE=5+4=9.
故答案为:9.
15.(2024秋 青羊区校级期中)如图,在△ABC中,按以下步骤作图:①分别以点B和C为圆心,以大于的长为半径作弧,两弧相交于点M和N;②作直线MN交AC于点D,连接BD,若AB=9,AC=20.则△ABD的周长为 29 .
【解答】解:由作图过程可知,直线MN为线段BC的垂直平分线,
∴BD=CD,
∴△ABD的周长为AB+AD+BD=AB+AD+CD=AB+AC=9+20=29.
故答案为:29.
16.(2024秋 红桥区期中)如图在△ABC中,AB=AC,D是BC上任意一点,DE⊥AB,DF⊥AC,若AB=10cm,S△ABC=25cm2,则DE+DF的长为 5 cm.
【解答】解:如图,连接AD,
∵AB=AC,DE⊥AB,DF⊥AC,
∴S△ABC=S△ABD+S△ADC=AB DE+AC DF=AB(DE+DF),
∵AB=10cm,S△ABC=25cm2,
∴,
解得:DE+DF=5(cm),
故答案为:5.
三.解答题(共6小题)
17.(2024秋 中山区期中)如图,∠CAE是△ABC的外角,AB=AC.
(1)请作出∠CAE的角平分线AD;(要求:尺规作图,保留作图痕迹,不写作法)
(2)求证:AD∥BC.
【解答】(1)解:如图,射线AD即为所求.
(2)证明:∵AB=AC,
∴∠B=∠C,
∴∠EAC=∠B+∠C=2∠B.
∵AD为∠EAC的平分线,
∴∠EAD=∠CAD,
∴∠EAC=2∠EAD,
∴∠EAD=∠B,
∴AD∥BC.
18.(2024秋 沾益区期中)如图,在平面直角坐标系中△ABC的顶点坐标分别是A(0,1),B(2,0),C(4,3).
(1)画出△ABC关于y轴对称的图形△AB1C1,并写出C1的坐标;
(2)已知点P是x轴上一点,若△BCP的面积等于△ABC面积的3倍,求点P的坐标.
【解答】解:(1)如图,△AB1C1即为所求.
由图可得,C1的坐标为(﹣4,3).
(2)△ABC的面积为=8﹣1﹣3=4.
设点P的坐标为(m,0),
∵△BCP的面积等于△ABC面积的3倍,
∴,
解得m=﹣6或10,
∴点P的坐标为(﹣6,0)或(10,0).
19.(2024秋 浦北县期中)如图,在△ABC是等边三角形,CD是中线,过B作BE∥CD,交AC延长线于点E.
(1)求∠E的度数;
(2)求证:BC是△ABE的中线.
【解答】(1)解:∵△ABC是等边三角形,CD是中线,
∴CD平分∠ACB,
∴,
∵BE∥CD,
∴∠ACD=∠E=30°;
(2)证明:由(1)可知,∠BCD=30°,∠E=30°,
∵BE∥CD,
∴∠BCD=∠CBE=30°,
∴∠CBE=∠E,
∴BC=CE,
∵在等边△ABC中,AC=BC,
∴AC=CE,
∴BC是△ABE的中线.
20.(2024秋 新源县期中)如图,在△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=6,求△ADE的周长;
(2)若∠BAC=130°,求∠DAE的度数.
【解答】解:(1)在△ABC中,边AB、AC的垂直平分线分别交BC于D、E,
∴DB=DA,EA=EC,
又BC=6,
∴△ADE的周长=AD+DE+EA=BD+DE+EC=BC=6;
(2)∵∠BAC=130°,
∴∠B+∠C=50°,
∵DA=DB,EA=EC,
∴∠BAD=∠B,∠EAC=∠C,
∴∠BAD+∠EAC=50°,
∴∠DAE=∠BAC﹣(∠BAD+∠EAC)=130°﹣50°=80°.
21.(2024春 丰城市校级期末)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长.
(2)若∠ABC=30°,∠C=45°,求∠CDE的度数.
【解答】解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为19,△DEC的周长为7,
∴AB+BE+CE+CD+AD=19,CD+EC+DE=CD+CE+AD=7,
∴AB+BE=19﹣7=12,
∴AB=BE=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
在△BAD和△BED中,
,
∴△BAD≌△BED(SSS),
∴∠BED=∠BAC=105°,
∴∠CDE=∠BED﹣∠C=105°﹣45°=60°.
22.(2024秋 宜兴市月考)如图,在△ABC中,点E是BC边上的一点,连接AE,BD垂直平分AE,垂足为F,交AC于点D.连接DE.
(1)若△ABC的周长为19,△DEC的周长为7,求AB的长;
(2)若∠ABC=30°,∠C=45°,求∠EAC的度数.
【解答】解:(1)∵BD是线段AE的垂直平分线,
∴AB=BE,AD=DE,
∵△ABC的周长为19,△DEC的周长为7,
∴AB+BE+CE+CD+AD=19,CD+EC+DE=CD+CE+AD=7,
∴AB+BE=19﹣7=12,
∴AB=BE=6;
(2)∵∠ABC=30°,∠C=45°,
∴∠BAC=180°﹣30°﹣45°=105°,
∵AB=BE,
∴,
∴∠EAC=∠BAC﹣∠BAE=30°.
