第12章全等三角形章末检测卷(含答案)2024-2025学年人教版数学八年级上册
文档属性
| 名称 | 第12章全等三角形章末检测卷(含答案)2024-2025学年人教版数学八年级上册 |

|
|
| 格式 | docx | ||
| 文件大小 | 623.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 20:55:42 | ||
图片预览



文档简介
第12章全等三角形章末检测卷-2024-2025学年数学八年级上册人教版
一.选择题(共8小题)
1.(2024秋 利通区校级月考)已知图中的两个三角形全等,则∠1的度数是( )
A.76° B.60° C.54° D.50°
2.(2024春 织金县期末)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.ASA B.SAS C.AAS D.SSS
3.(2023秋 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
4.(2023秋 苍梧县期末)如图所示,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BE等于( )
A.4cm B.3cm C.2cm D.1cm
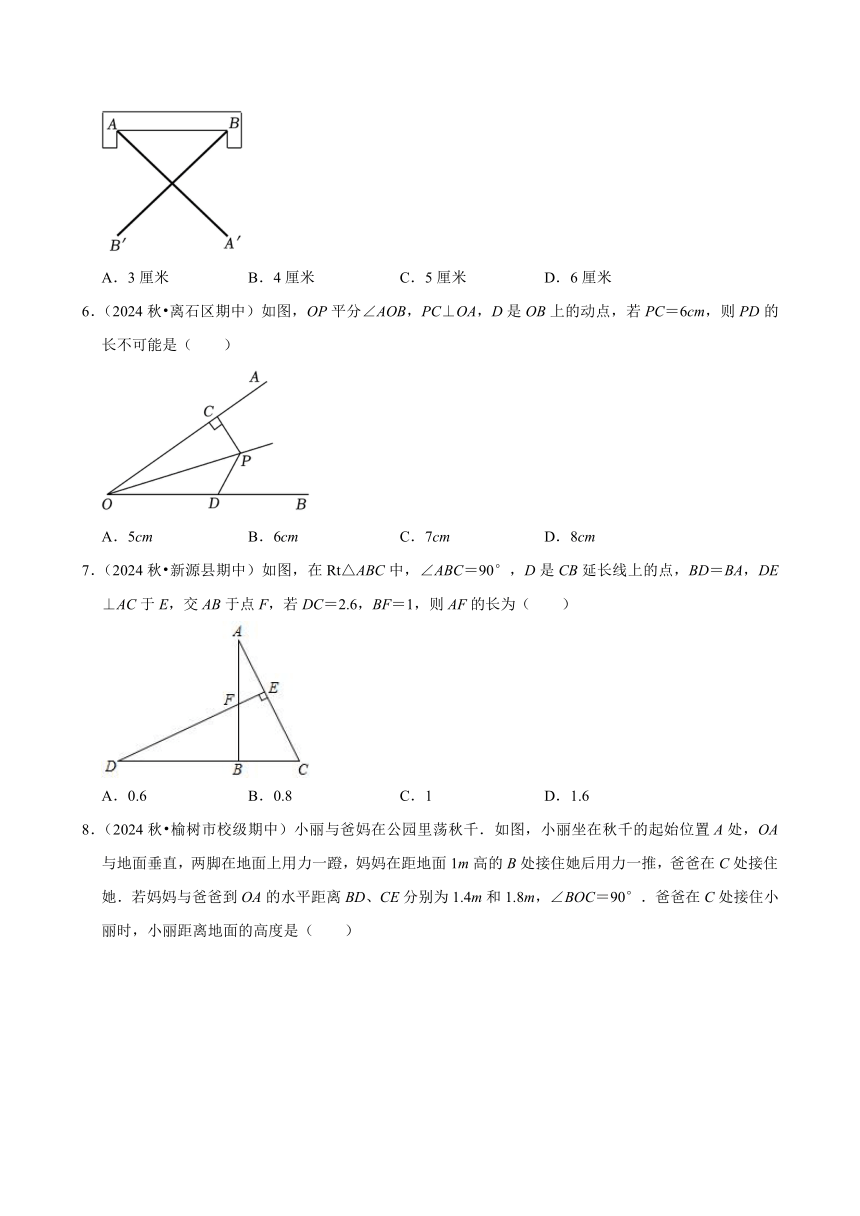
5.(2024秋 浦北县期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得A′B′=5厘米,则这个工件得内槽宽为( )
A.3厘米 B.4厘米 C.5厘米 D.6厘米
6.(2024秋 离石区期中)如图,OP平分∠AOB,PC⊥OA,D是OB上的动点,若PC=6cm,则PD的长不可能是( )
A.5cm B.6cm C.7cm D.8cm
7.(2024秋 新源县期中)如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
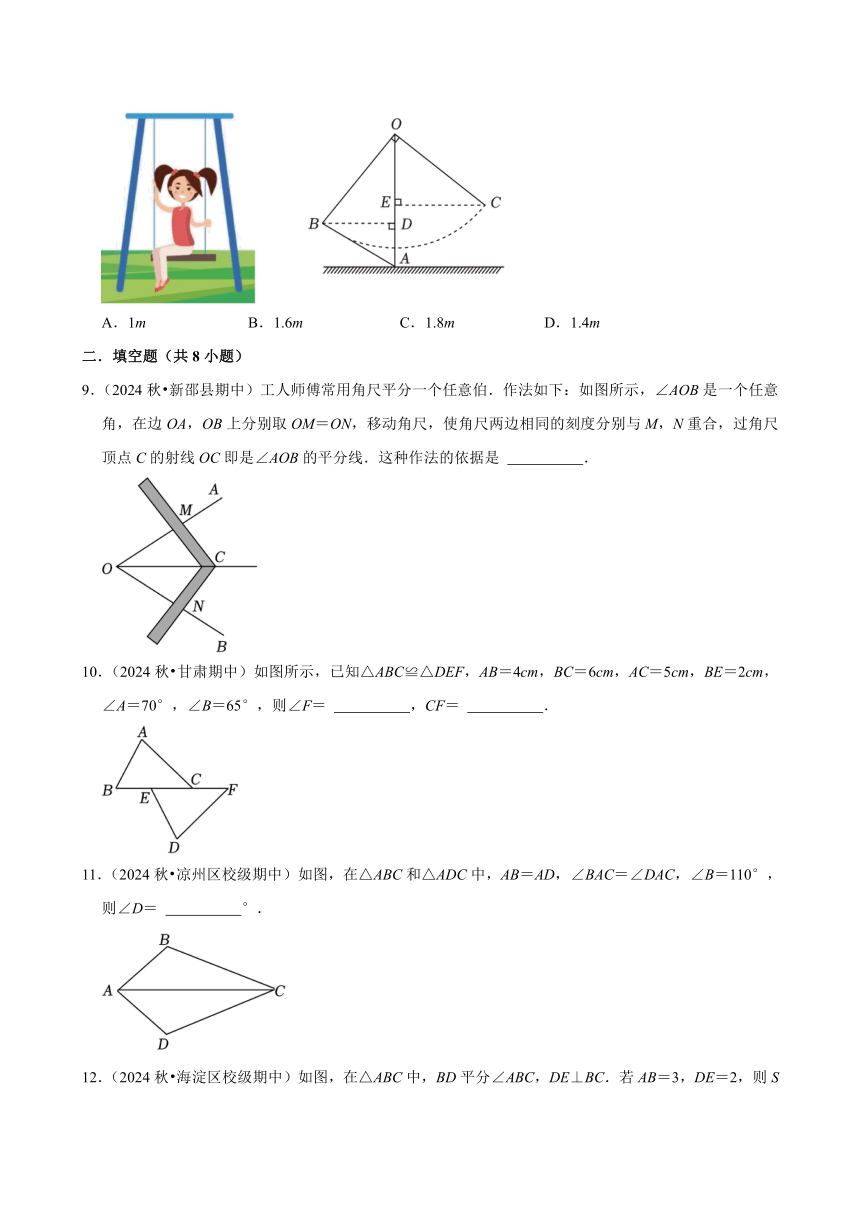
8.(2024秋 榆树市校级期中)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.6m C.1.8m D.1.4m
二.填空题(共8小题)
9.(2024秋 新邵县期中)工人师傅常用角尺平分一个任意伯.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是 .
10.(2024秋 甘肃期中)如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,BE=2cm,∠A=70°,∠B=65°,则∠F= ,CF= .
11.(2024秋 凉州区校级期中)如图,在△ABC和△ADC中,AB=AD,∠BAC=∠DAC,∠B=110°,则∠D= °.
12.(2024秋 海淀区校级期中)如图,在△ABC中,BD平分∠ABC,DE⊥BC.若AB=3,DE=2,则S△ABD= .
13.(2024秋 柳南区校级期中)如图,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为 .
14.(2024秋 姜堰区期中)如图,点M是∠AOB的平分线上一点,过点M作MC⊥OA,垂足为点C.若MC=4,点D是OB上任意一点,则MD的最小值为 .
15.(2024秋 榆树市校级期中)如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连结GC,使∠G=∠BAD.有以下四个结论:
①△BED≌△CFD;
②若点A为FG中点,则FG=4DE;
③若AF=CF,则AG=BE;
④△AGC的面积是△BDE面积的2倍.
以上结论中正确的为 .(只填写序号)
16.(2024秋 凉州区期中)如图,在四边形ABCD中,∠B=90°,AD=BC=6,AB=8,若AC平分∠BAD,则四边形ABCD的面积为 .
三.解答题(共6小题)
17.(2024秋 萧山区校级月考)如图,已知AB∥CD,AB=CD,点E、F在BC上,BE=CF.求证:AF=DE.
18.(2024秋 姜堰区期中)如图,在△ABC中,AB=AC,点D在BC上,且AD=BD.
(1)求证:∠ADB=∠BAC;
(2)若E为BC中点,∠DAE=36°,求∠EAC的度数.
19.(2024秋 凉州区期中)如图,点E在△ABC外部,点D在边BC上,DE交AC于点F,若∠1=∠2=∠3,AB=AD,
(1)求证:△ABC≌△ADE.
(2)若AF=FC,EF=3DF,且S△DFC=1,则△ABC的面积是多少?
20.(2024秋 天河区校级期中)如图,在Rt△ABC中,∠C=90°,点D在AC边上,DE⊥AB于点E,点F在BC边上,DF=AD,CF=AE,连接BD.
(1)求证:BD平分∠ABC;
(2)若AB=10,CF=2,求线段BF的长.
21.(2024秋 离石区期中)(1)已知△ABC的三边长是a,b,c,若a=4,b=6,且三角形的周长是小于15的奇数.求边长c的值.
(2)图1是小宁制作的燕子风筝,燕子风箏的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=40°,求∠D的度数.
22.(2024秋 榆树市校级期中)如图①,∠A=∠D=90°,AB=DC,点E、F在直线BC上,且BE=CF.
(1)求证:AF=DE;
(2)如图②,连结图①中的AE、DF,设DE、AF交于点G,过点G作GH⊥BC于点H,在不添加辅助线和连结其它线的前提下,直接写出图②中的3对全等三角形.(已证明过的除外)
第12章全等三角形章末检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 利通区校级月考)已知图中的两个三角形全等,则∠1的度数是( )
A.76° B.60° C.54° D.50°
【解答】解:∵两个三角形全等,∠1是a、b之间的夹角,
∴∠1=180°﹣54°﹣76°=50°,
故选:D.
2.(2024春 织金县期末)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.ASA B.SAS C.AAS D.SSS
【解答】解:画一个三角形A′B′C′,使∠A′=∠A,A′B′=AB,∠B′=∠B,
符合全等三角形的判定定理ASA,
故选:A.
3.(2023秋 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
【解答】解:∵△ABC≌△DEC,
∴BC=CE,∠DCE=∠ACB,
∴∠CEB=∠B=70°,
∴∠ECB=180°﹣∠CEB﹣∠B=40°,
∵∠ACD+∠ACE=∠ECB+∠ACE,
∴∠ACD=∠ECB=40°.
故选:B.
4.(2023秋 苍梧县期末)如图所示,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BE等于( )
A.4cm B.3cm C.2cm D.1cm
【解答】解:∵AC⊥BC,AD为∠BAC的平分线,DE⊥AB,
∴∠ADC=∠ADE,
∴AE=AC=3,
∴BE=AB﹣AE=7﹣3=4(cm).
故选:A.
5.(2024秋 浦北县期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得A′B′=5厘米,则这个工件得内槽宽为( )
A.3厘米 B.4厘米 C.5厘米 D.6厘米
【解答】解:连接A′B′,如图,
在△OAB和△OA′B′中,
,
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(厘米).
∴这个工件得内槽宽为5厘米.
故选:C.
6.(2024秋 离石区期中)如图,OP平分∠AOB,PC⊥OA,D是OB上的动点,若PC=6cm,则PD的长不可能是( )
A.5cm B.6cm C.7cm D.8cm
【解答】解:过点P作PE⊥OB于点E,如图,
∵OP平分∠AOB,PC⊥OA,PC=6cm,D是OB上的动点,
∴PE=PC=6cm,
∴PD≥6cm,
∴5cm不符合题意,
故选:A.
7.(2024秋 新源县期中)如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
【解答】解:∵DE⊥AC于E,
∴∠FDB+∠C=90°,
∵∠ABC=90°,
∴∠D+∠DFB=90°,
∴∠C=∠BFD,
在△DBF与△ABC中,
,
∴△DBF≌△ABC(AAS),
∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
8.(2024秋 榆树市校级期中)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.6m C.1.8m D.1.4m
【解答】解:∵∠BOC=90°,
∴∠BOD+∠COE=90°,
由题意可知,OB=CO,DA=1m,BD⊥OA,CE⊥OA,
∵∠BDO=∠OEC=90°,
∴∠BOD+∠OBD=90°,
∴∠COE=∠OBD,
在△OBD和△COE中,
,
∴△OBD≌△COE(AAS),
∴OE=BD=1.4m,OD=CE=1.8m,
∴AE=OA﹣OE=OD+DA﹣OE=1.8+1﹣1.4=1.4(m),
即小丽距离地面的高度是1.4m,
故选:D.
二.填空题(共8小题)
9.(2024秋 新邵县期中)工人师傅常用角尺平分一个任意伯.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是 SSS .
【解答】解:由图可知:CM=CN,
在△COM和△CON中,
,
∴△COM≌△CON(SSS),
∴∠MOC=∠NOC,
∴OC是∠AOB的平分线,
故答案为:SSS.
10.(2024秋 甘肃期中)如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,BE=2cm,∠A=70°,∠B=65°,则∠F= 45° ,CF= 2cm .
【解答】解:∵∠A=70°,∠B=65°,
∴∠ACB=180°﹣70°﹣65°=45°,
∵△ABC≌△DEF,
∴∠F=∠ACB=45°,EF=BC,
∴CF=BE=2cm.
故答案为:45°,2cm.
11.(2024秋 凉州区校级期中)如图,在△ABC和△ADC中,AB=AD,∠BAC=∠DAC,∠B=110°,则∠D= 110 °.
【解答】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∵∠B=110°,
∴∠D=110°,
故答案为:110.
12.(2024秋 海淀区校级期中)如图,在△ABC中,BD平分∠ABC,DE⊥BC.若AB=3,DE=2,则S△ABD= 3 .
【解答】解:过点D作DF⊥BA,垂足为F,
∵BD平分∠ABC,DE⊥BC,DF⊥BA,
∴DE=DF=2,
∵AB=3,
∴S△ABD=AB DF=×3×2=3.
故答案为:3.
13.(2024秋 柳南区校级期中)如图,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为 40° .
【解答】解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
即∠BAD+∠DAC=∠DAC+∠CAE,
∴∠CAE=∠BAD=40°.
故答案为:40°.
14.(2024秋 姜堰区期中)如图,点M是∠AOB的平分线上一点,过点M作MC⊥OA,垂足为点C.若MC=4,点D是OB上任意一点,则MD的最小值为 4 .
【解答】解:∵点M是∠AOB的平分线上一点,MC⊥OA,
∴当DM⊥OB时,MD=MC,此时MD的值最小,
∵MC=4,
∴MD的最小值为4.
故答案为:4.
15.(2024秋 榆树市校级期中)如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连结GC,使∠G=∠BAD.有以下四个结论:
①△BED≌△CFD;
②若点A为FG中点,则FG=4DE;
③若AF=CF,则AG=BE;
④△AGC的面积是△BDE面积的2倍.
以上结论中正确的为 ①②④ .(只填写序号)
【解答】解:∵AD为中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=∠GFC=90°,
在△BED和△CFD中,
,
∴△BDE≌△CDF(AAS),
故结论①正确;
②∵△BDE≌△CDF,
∴BE=CF,DE=DF,
∴EF=2DE,
在△ABE和△GCF中,
,
∴△ABE≌△GCF(AAS),
∴AE=GF,
即AF+EF=AG+AF,
∴EF=AG,
∵点A为FG中点,
∴FG=2AG,
∴FG=2EF=4DE,
故结论②正确;
③∵AF=CF,BE=CF,
∴AF=BE,
当点A为FG中点时,AG=AF=BE,
∵点A不一定是FG中点,
∴AG,BE不一定相等,
故结论③错误;
④∵EF=AG,ED=FD,
∴AG=2DE,
∵BE=CF,BE⊥AD,CF⊥AD,
∴S△AGC=AG CF=DE CF,S△BDE=BE DE=BE CF,
S△AGC=2S△BDE,
故结论④正确,
综上所述:结论中正确的为①②④.
故答案为:①②④.
16.(2024秋 凉州区期中)如图,在四边形ABCD中,∠B=90°,AD=BC=6,AB=8,若AC平分∠BAD,则四边形ABCD的面积为 42 .
【解答】解:如图,作CE⊥AD的延长线于E,
由角平分线的性质可知:CE=BC=6,
∴,
故答案为:42.
三.解答题(共6小题)
17.(2024秋 萧山区校级月考)如图,已知AB∥CD,AB=CD,点E、F在BC上,BE=CF.求证:AF=DE.
【解答】证明:∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BF=CE,
在△ABF与△DCF中,
∴△ABF≌△DCE(SAS),
∴AF=DE.
18.(2024秋 姜堰区期中)如图,在△ABC中,AB=AC,点D在BC上,且AD=BD.
(1)求证:∠ADB=∠BAC;
(2)若E为BC中点,∠DAE=36°,求∠EAC的度数.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠DAB=∠B,
∴∠ADB=∠BAC;
(2)解:∵AB=AC,E为BC中点,
∴AE⊥BC,
∴∠AED=∠AEC=90°,
∵∠DAE=36°,
∴∠ADE=90°﹣36°=54°,
∵AD=BD,
∴∠DAB=∠B=27°,
∵AB=AC,
∴∠B=∠C=27°,
∴∠EAC=90°﹣27°=63°.
19.(2024秋 凉州区期中)如图,点E在△ABC外部,点D在边BC上,DE交AC于点F,若∠1=∠2=∠3,AB=AD,
(1)求证:△ABC≌△ADE.
(2)若AF=FC,EF=3DF,且S△DFC=1,则△ABC的面积是多少?
【解答】(1)证明:∵∠1=∠2=∠3,
∴∠1+∠DAF=∠2+∠DAF
即∠BAC=∠DAE,
∵∠2=∠3,∠AFE=∠CFD,
∵∠E=180°﹣∠2﹣∠AFE,
∵∠C=180°﹣∠3﹣∠CFD,
∴∠E=∠C,
在△BAC和△DAE中,
,
∴△ABC≌△ADE(AAS);
(2)解:∵AF=FC,
∴S△ADF=S△CDF,
∵,,
∵EF=3DF,
∴S△AEF=3S△DAF=3S△DFC=3,
∴S△ABC=S△DAE=S△DAF+S△AFE=4.
20.(2024秋 天河区校级期中)如图,在Rt△ABC中,∠C=90°,点D在AC边上,DE⊥AB于点E,点F在BC边上,DF=AD,CF=AE,连接BD.
(1)求证:BD平分∠ABC;
(2)若AB=10,CF=2,求线段BF的长.
【解答】(1)证明:∵DE⊥AB,
∴∠BED=∠AED=90°,
在Rt△ADE和Rt△FDC中,
,
∴Rt△ADE≌Rt△FDC(HL),
∴DC=DE,
又∵DC⊥BC,DE⊥BA,
∴BD平分∠ABC;
(2)解:在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BC=BE,
∵AE=CF,CF=2,
∴AE=2,
∵AB=10,
∴BE=AB﹣AE=10﹣2=8,
∴BC=8,
∴BF=BC﹣CF=8﹣2=6,
∴BF=6.
21.(2024秋 离石区期中)(1)已知△ABC的三边长是a,b,c,若a=4,b=6,且三角形的周长是小于15的奇数.求边长c的值.
(2)图1是小宁制作的燕子风筝,燕子风箏的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=40°,求∠D的度数.
【解答】解:(1)∵a=4,b=6,
∴2<c<10,
∵a+b+c=10+c,
三角形的周长是小于15的奇数,
∴10+c<15,
∴c为2<c<5的奇数,
∴c=3;
(2)∵∠BAD=∠EAC,
∴∠BAC=∠EAD,
在△BAC与△EAD中,
,
∴△BAC≌△EAD(SAS),
∴∠D=∠C=40°.
22.(2024秋 榆树市校级期中)如图①,∠A=∠D=90°,AB=DC,点E、F在直线BC上,且BE=CF.
(1)求证:AF=DE;
(2)如图②,连结图①中的AE、DF,设DE、AF交于点G,过点G作GH⊥BC于点H,在不添加辅助线和连结其它线的前提下,直接写出图②中的3对全等三角形.(已证明过的除外)
【解答】(1)证明:∵BE=CF,
∴BF=EC,
∵AB=DC,BE=EC,
∴Rt△ABF≌Rt△DCE(HL),
∴AF=DE;
(2)解:∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴GE=GF,
又∵GH=GH,
∴Rt△GHE≌Rt△GHF(HL),
∵AF=DE,GE=GF,
∴AG=DG,
又∵∠AGE=∠DGF,EG=GF,
∴△AGE≌△DGF(SAS),
∴AE=DF,
又∵BE=CF,AB=DC,
∴△ABE≌△DCF(SSS).
一.选择题(共8小题)
1.(2024秋 利通区校级月考)已知图中的两个三角形全等,则∠1的度数是( )
A.76° B.60° C.54° D.50°
2.(2024春 织金县期末)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.ASA B.SAS C.AAS D.SSS
3.(2023秋 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
4.(2023秋 苍梧县期末)如图所示,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BE等于( )
A.4cm B.3cm C.2cm D.1cm
5.(2024秋 浦北县期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得A′B′=5厘米,则这个工件得内槽宽为( )
A.3厘米 B.4厘米 C.5厘米 D.6厘米
6.(2024秋 离石区期中)如图,OP平分∠AOB,PC⊥OA,D是OB上的动点,若PC=6cm,则PD的长不可能是( )
A.5cm B.6cm C.7cm D.8cm
7.(2024秋 新源县期中)如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
8.(2024秋 榆树市校级期中)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.6m C.1.8m D.1.4m
二.填空题(共8小题)
9.(2024秋 新邵县期中)工人师傅常用角尺平分一个任意伯.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是 .
10.(2024秋 甘肃期中)如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,BE=2cm,∠A=70°,∠B=65°,则∠F= ,CF= .
11.(2024秋 凉州区校级期中)如图,在△ABC和△ADC中,AB=AD,∠BAC=∠DAC,∠B=110°,则∠D= °.
12.(2024秋 海淀区校级期中)如图,在△ABC中,BD平分∠ABC,DE⊥BC.若AB=3,DE=2,则S△ABD= .
13.(2024秋 柳南区校级期中)如图,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为 .
14.(2024秋 姜堰区期中)如图,点M是∠AOB的平分线上一点,过点M作MC⊥OA,垂足为点C.若MC=4,点D是OB上任意一点,则MD的最小值为 .
15.(2024秋 榆树市校级期中)如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连结GC,使∠G=∠BAD.有以下四个结论:
①△BED≌△CFD;
②若点A为FG中点,则FG=4DE;
③若AF=CF,则AG=BE;
④△AGC的面积是△BDE面积的2倍.
以上结论中正确的为 .(只填写序号)
16.(2024秋 凉州区期中)如图,在四边形ABCD中,∠B=90°,AD=BC=6,AB=8,若AC平分∠BAD,则四边形ABCD的面积为 .
三.解答题(共6小题)
17.(2024秋 萧山区校级月考)如图,已知AB∥CD,AB=CD,点E、F在BC上,BE=CF.求证:AF=DE.
18.(2024秋 姜堰区期中)如图,在△ABC中,AB=AC,点D在BC上,且AD=BD.
(1)求证:∠ADB=∠BAC;
(2)若E为BC中点,∠DAE=36°,求∠EAC的度数.
19.(2024秋 凉州区期中)如图,点E在△ABC外部,点D在边BC上,DE交AC于点F,若∠1=∠2=∠3,AB=AD,
(1)求证:△ABC≌△ADE.
(2)若AF=FC,EF=3DF,且S△DFC=1,则△ABC的面积是多少?
20.(2024秋 天河区校级期中)如图,在Rt△ABC中,∠C=90°,点D在AC边上,DE⊥AB于点E,点F在BC边上,DF=AD,CF=AE,连接BD.
(1)求证:BD平分∠ABC;
(2)若AB=10,CF=2,求线段BF的长.
21.(2024秋 离石区期中)(1)已知△ABC的三边长是a,b,c,若a=4,b=6,且三角形的周长是小于15的奇数.求边长c的值.
(2)图1是小宁制作的燕子风筝,燕子风箏的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=40°,求∠D的度数.
22.(2024秋 榆树市校级期中)如图①,∠A=∠D=90°,AB=DC,点E、F在直线BC上,且BE=CF.
(1)求证:AF=DE;
(2)如图②,连结图①中的AE、DF,设DE、AF交于点G,过点G作GH⊥BC于点H,在不添加辅助线和连结其它线的前提下,直接写出图②中的3对全等三角形.(已证明过的除外)
第12章全等三角形章末检测卷-2024-2025学年数学八年级上册人教版
参考答案与试题解析
一.选择题(共8小题)
1.(2024秋 利通区校级月考)已知图中的两个三角形全等,则∠1的度数是( )
A.76° B.60° C.54° D.50°
【解答】解:∵两个三角形全等,∠1是a、b之间的夹角,
∴∠1=180°﹣54°﹣76°=50°,
故选:D.
2.(2024春 织金县期末)如图所示,亮亮书上的三角形被墨迹污染了一部分,很快他就根据所学知识画出一个与书上完全一样的三角形,那么这两个三角形完全一样的依据是( )
A.ASA B.SAS C.AAS D.SSS
【解答】解:画一个三角形A′B′C′,使∠A′=∠A,A′B′=AB,∠B′=∠B,
符合全等三角形的判定定理ASA,
故选:A.
3.(2023秋 黑龙江期末)如图,△ABC≌△DEC,点E在AB边上,∠B=70°,则∠ACD的度数为( )
A.30° B.40° C.45° D.50°
【解答】解:∵△ABC≌△DEC,
∴BC=CE,∠DCE=∠ACB,
∴∠CEB=∠B=70°,
∴∠ECB=180°﹣∠CEB﹣∠B=40°,
∵∠ACD+∠ACE=∠ECB+∠ACE,
∴∠ACD=∠ECB=40°.
故选:B.
4.(2023秋 苍梧县期末)如图所示,在△ABC中,AC⊥BC,AD为∠BAC的平分线,DE⊥AB,AB=7cm,AC=3cm,则BE等于( )
A.4cm B.3cm C.2cm D.1cm
【解答】解:∵AC⊥BC,AD为∠BAC的平分线,DE⊥AB,
∴∠ADC=∠ADE,
∴AE=AC=3,
∴BE=AB﹣AE=7﹣3=4(cm).
故选:A.
5.(2024秋 浦北县期中)如图,把两根钢条AA′,BB′的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),若测得A′B′=5厘米,则这个工件得内槽宽为( )
A.3厘米 B.4厘米 C.5厘米 D.6厘米
【解答】解:连接A′B′,如图,
在△OAB和△OA′B′中,
,
∴△OAB≌△OA′B′(SAS),
∴A′B′=AB=5(厘米).
∴这个工件得内槽宽为5厘米.
故选:C.
6.(2024秋 离石区期中)如图,OP平分∠AOB,PC⊥OA,D是OB上的动点,若PC=6cm,则PD的长不可能是( )
A.5cm B.6cm C.7cm D.8cm
【解答】解:过点P作PE⊥OB于点E,如图,
∵OP平分∠AOB,PC⊥OA,PC=6cm,D是OB上的动点,
∴PE=PC=6cm,
∴PD≥6cm,
∴5cm不符合题意,
故选:A.
7.(2024秋 新源县期中)如图,在Rt△ABC中,∠ABC=90°,D是CB延长线上的点,BD=BA,DE⊥AC于E,交AB于点F,若DC=2.6,BF=1,则AF的长为( )
A.0.6 B.0.8 C.1 D.1.6
【解答】解:∵DE⊥AC于E,
∴∠FDB+∠C=90°,
∵∠ABC=90°,
∴∠D+∠DFB=90°,
∴∠C=∠BFD,
在△DBF与△ABC中,
,
∴△DBF≌△ABC(AAS),
∴BF=BC,
∵DC=2.6,BF=1,
∴AF=AB﹣BF=BD﹣BF=DC﹣BF﹣BF=2.6﹣1﹣1=0.6,
故选:A.
8.(2024秋 榆树市校级期中)小丽与爸妈在公园里荡秋千.如图,小丽坐在秋千的起始位置A处,OA与地面垂直,两脚在地面上用力一蹬,妈妈在距地面1m高的B处接住她后用力一推,爸爸在C处接住她.若妈妈与爸爸到OA的水平距离BD、CE分别为1.4m和1.8m,∠BOC=90°.爸爸在C处接住小丽时,小丽距离地面的高度是( )
A.1m B.1.6m C.1.8m D.1.4m
【解答】解:∵∠BOC=90°,
∴∠BOD+∠COE=90°,
由题意可知,OB=CO,DA=1m,BD⊥OA,CE⊥OA,
∵∠BDO=∠OEC=90°,
∴∠BOD+∠OBD=90°,
∴∠COE=∠OBD,
在△OBD和△COE中,
,
∴△OBD≌△COE(AAS),
∴OE=BD=1.4m,OD=CE=1.8m,
∴AE=OA﹣OE=OD+DA﹣OE=1.8+1﹣1.4=1.4(m),
即小丽距离地面的高度是1.4m,
故选:D.
二.填空题(共8小题)
9.(2024秋 新邵县期中)工人师傅常用角尺平分一个任意伯.作法如下:如图所示,∠AOB是一个任意角,在边OA,OB上分别取OM=ON,移动角尺,使角尺两边相同的刻度分别与M,N重合,过角尺顶点C的射线OC即是∠AOB的平分线.这种作法的依据是 SSS .
【解答】解:由图可知:CM=CN,
在△COM和△CON中,
,
∴△COM≌△CON(SSS),
∴∠MOC=∠NOC,
∴OC是∠AOB的平分线,
故答案为:SSS.
10.(2024秋 甘肃期中)如图所示,已知△ABC≌△DEF,AB=4cm,BC=6cm,AC=5cm,BE=2cm,∠A=70°,∠B=65°,则∠F= 45° ,CF= 2cm .
【解答】解:∵∠A=70°,∠B=65°,
∴∠ACB=180°﹣70°﹣65°=45°,
∵△ABC≌△DEF,
∴∠F=∠ACB=45°,EF=BC,
∴CF=BE=2cm.
故答案为:45°,2cm.
11.(2024秋 凉州区校级期中)如图,在△ABC和△ADC中,AB=AD,∠BAC=∠DAC,∠B=110°,则∠D= 110 °.
【解答】解:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∵∠B=110°,
∴∠D=110°,
故答案为:110.
12.(2024秋 海淀区校级期中)如图,在△ABC中,BD平分∠ABC,DE⊥BC.若AB=3,DE=2,则S△ABD= 3 .
【解答】解:过点D作DF⊥BA,垂足为F,
∵BD平分∠ABC,DE⊥BC,DF⊥BA,
∴DE=DF=2,
∵AB=3,
∴S△ABD=AB DF=×3×2=3.
故答案为:3.
13.(2024秋 柳南区校级期中)如图,△ABC≌△ADE,若∠BAD=40°,则∠CAE的度数为 40° .
【解答】解:∵△ABC≌△ADE,
∴∠BAC=∠DAE,
即∠BAD+∠DAC=∠DAC+∠CAE,
∴∠CAE=∠BAD=40°.
故答案为:40°.
14.(2024秋 姜堰区期中)如图,点M是∠AOB的平分线上一点,过点M作MC⊥OA,垂足为点C.若MC=4,点D是OB上任意一点,则MD的最小值为 4 .
【解答】解:∵点M是∠AOB的平分线上一点,MC⊥OA,
∴当DM⊥OB时,MD=MC,此时MD的值最小,
∵MC=4,
∴MD的最小值为4.
故答案为:4.
15.(2024秋 榆树市校级期中)如图,在△ABC中,AD为中线,过点B作BE⊥AD于点E,过点C作CF⊥AD于点F.在DA延长线上取一点G,连结GC,使∠G=∠BAD.有以下四个结论:
①△BED≌△CFD;
②若点A为FG中点,则FG=4DE;
③若AF=CF,则AG=BE;
④△AGC的面积是△BDE面积的2倍.
以上结论中正确的为 ①②④ .(只填写序号)
【解答】解:∵AD为中线,
∴BD=CD,
∵BE⊥AD,CF⊥AD,
∴∠E=∠CFD=∠GFC=90°,
在△BED和△CFD中,
,
∴△BDE≌△CDF(AAS),
故结论①正确;
②∵△BDE≌△CDF,
∴BE=CF,DE=DF,
∴EF=2DE,
在△ABE和△GCF中,
,
∴△ABE≌△GCF(AAS),
∴AE=GF,
即AF+EF=AG+AF,
∴EF=AG,
∵点A为FG中点,
∴FG=2AG,
∴FG=2EF=4DE,
故结论②正确;
③∵AF=CF,BE=CF,
∴AF=BE,
当点A为FG中点时,AG=AF=BE,
∵点A不一定是FG中点,
∴AG,BE不一定相等,
故结论③错误;
④∵EF=AG,ED=FD,
∴AG=2DE,
∵BE=CF,BE⊥AD,CF⊥AD,
∴S△AGC=AG CF=DE CF,S△BDE=BE DE=BE CF,
S△AGC=2S△BDE,
故结论④正确,
综上所述:结论中正确的为①②④.
故答案为:①②④.
16.(2024秋 凉州区期中)如图,在四边形ABCD中,∠B=90°,AD=BC=6,AB=8,若AC平分∠BAD,则四边形ABCD的面积为 42 .
【解答】解:如图,作CE⊥AD的延长线于E,
由角平分线的性质可知:CE=BC=6,
∴,
故答案为:42.
三.解答题(共6小题)
17.(2024秋 萧山区校级月考)如图,已知AB∥CD,AB=CD,点E、F在BC上,BE=CF.求证:AF=DE.
【解答】证明:∵AB∥CD,
∴∠B=∠C,
∵BE=CF,
∴BF=CE,
在△ABF与△DCF中,
∴△ABF≌△DCE(SAS),
∴AF=DE.
18.(2024秋 姜堰区期中)如图,在△ABC中,AB=AC,点D在BC上,且AD=BD.
(1)求证:∠ADB=∠BAC;
(2)若E为BC中点,∠DAE=36°,求∠EAC的度数.
【解答】(1)证明:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠DAB=∠B,
∴∠ADB=∠BAC;
(2)解:∵AB=AC,E为BC中点,
∴AE⊥BC,
∴∠AED=∠AEC=90°,
∵∠DAE=36°,
∴∠ADE=90°﹣36°=54°,
∵AD=BD,
∴∠DAB=∠B=27°,
∵AB=AC,
∴∠B=∠C=27°,
∴∠EAC=90°﹣27°=63°.
19.(2024秋 凉州区期中)如图,点E在△ABC外部,点D在边BC上,DE交AC于点F,若∠1=∠2=∠3,AB=AD,
(1)求证:△ABC≌△ADE.
(2)若AF=FC,EF=3DF,且S△DFC=1,则△ABC的面积是多少?
【解答】(1)证明:∵∠1=∠2=∠3,
∴∠1+∠DAF=∠2+∠DAF
即∠BAC=∠DAE,
∵∠2=∠3,∠AFE=∠CFD,
∵∠E=180°﹣∠2﹣∠AFE,
∵∠C=180°﹣∠3﹣∠CFD,
∴∠E=∠C,
在△BAC和△DAE中,
,
∴△ABC≌△ADE(AAS);
(2)解:∵AF=FC,
∴S△ADF=S△CDF,
∵,,
∵EF=3DF,
∴S△AEF=3S△DAF=3S△DFC=3,
∴S△ABC=S△DAE=S△DAF+S△AFE=4.
20.(2024秋 天河区校级期中)如图,在Rt△ABC中,∠C=90°,点D在AC边上,DE⊥AB于点E,点F在BC边上,DF=AD,CF=AE,连接BD.
(1)求证:BD平分∠ABC;
(2)若AB=10,CF=2,求线段BF的长.
【解答】(1)证明:∵DE⊥AB,
∴∠BED=∠AED=90°,
在Rt△ADE和Rt△FDC中,
,
∴Rt△ADE≌Rt△FDC(HL),
∴DC=DE,
又∵DC⊥BC,DE⊥BA,
∴BD平分∠ABC;
(2)解:在Rt△BCD与Rt△BED中,
,
∴Rt△BCD≌Rt△BED(HL),
∴BC=BE,
∵AE=CF,CF=2,
∴AE=2,
∵AB=10,
∴BE=AB﹣AE=10﹣2=8,
∴BC=8,
∴BF=BC﹣CF=8﹣2=6,
∴BF=6.
21.(2024秋 离石区期中)(1)已知△ABC的三边长是a,b,c,若a=4,b=6,且三角形的周长是小于15的奇数.求边长c的值.
(2)图1是小宁制作的燕子风筝,燕子风箏的骨架图如图2所示,AB=AE,AC=AD,∠BAD=∠EAC,∠C=40°,求∠D的度数.
【解答】解:(1)∵a=4,b=6,
∴2<c<10,
∵a+b+c=10+c,
三角形的周长是小于15的奇数,
∴10+c<15,
∴c为2<c<5的奇数,
∴c=3;
(2)∵∠BAD=∠EAC,
∴∠BAC=∠EAD,
在△BAC与△EAD中,
,
∴△BAC≌△EAD(SAS),
∴∠D=∠C=40°.
22.(2024秋 榆树市校级期中)如图①,∠A=∠D=90°,AB=DC,点E、F在直线BC上,且BE=CF.
(1)求证:AF=DE;
(2)如图②,连结图①中的AE、DF,设DE、AF交于点G,过点G作GH⊥BC于点H,在不添加辅助线和连结其它线的前提下,直接写出图②中的3对全等三角形.(已证明过的除外)
【解答】(1)证明:∵BE=CF,
∴BF=EC,
∵AB=DC,BE=EC,
∴Rt△ABF≌Rt△DCE(HL),
∴AF=DE;
(2)解:∵Rt△ABF≌Rt△DCE,
∴∠AFB=∠DEC,
∴GE=GF,
又∵GH=GH,
∴Rt△GHE≌Rt△GHF(HL),
∵AF=DE,GE=GF,
∴AG=DG,
又∵∠AGE=∠DGF,EG=GF,
∴△AGE≌△DGF(SAS),
∴AE=DF,
又∵BE=CF,AB=DC,
∴△ABE≌△DCF(SSS).
