江苏省江阴市南闸实验学校苏科版八年级数学上册期末复习---第3章《勾股定理》导学案(无答案)(无答案)
文档属性
| 名称 | 江苏省江阴市南闸实验学校苏科版八年级数学上册期末复习---第3章《勾股定理》导学案(无答案)(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 95.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 20:25:59 | ||
图片预览

文档简介
南闸实验学校初二数学期末复习------勾股定理、实数
(命题人:吴晓玲 审核:初二数学组) 班级 姓名
一、重点题型
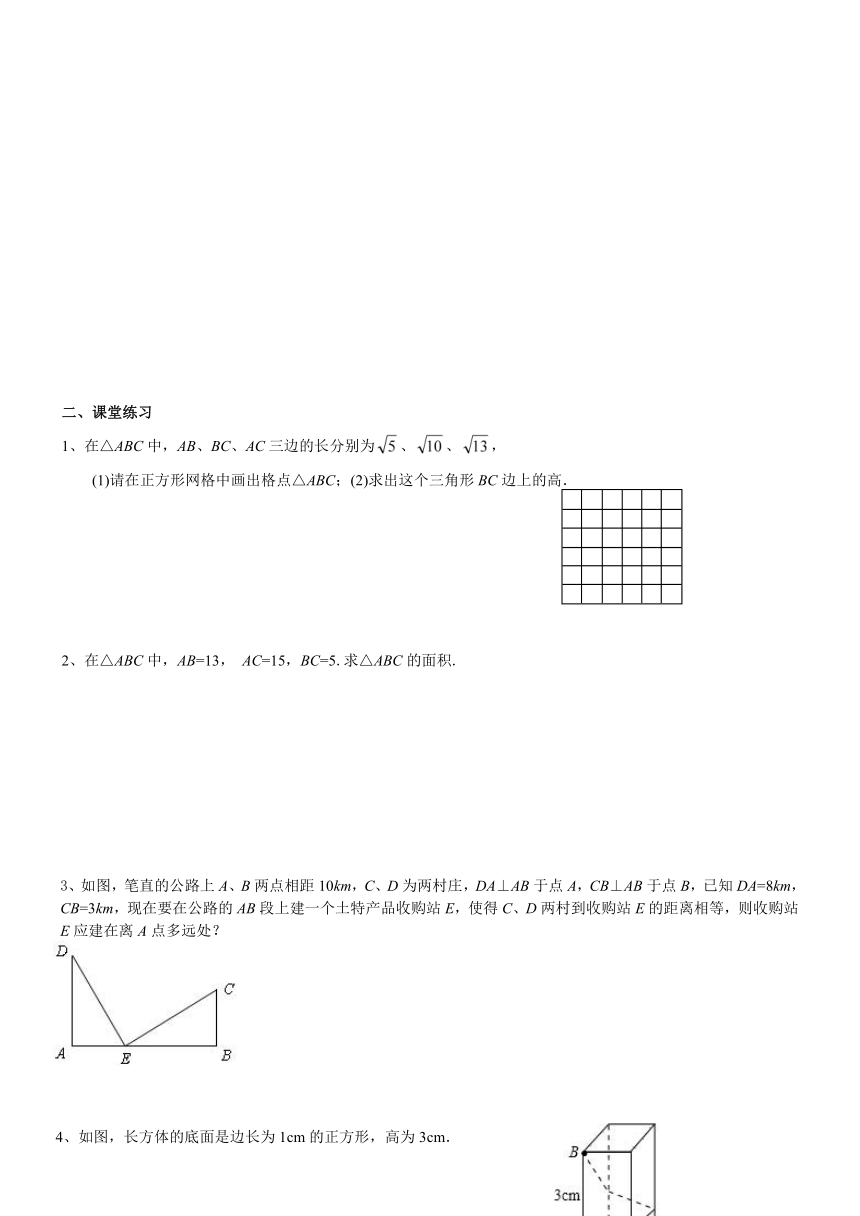
例1、如图,每个方格都是边长为1的正方形,
(1)求四边形ABCD的周长和面积;
(2)求∠ABC的度数,并说明理由。
例2、在△ABC中,AD是BC边上的高,若AB=l0,AD=8,AC=17,求△ABC的面积.
(画出示意图)
例3、如图是一个长、宽、高分别是4cm、 ( http: / / www.21cnjy.com )1cm和2cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,求它需要爬行的最短路径的长.
例4、已知如图,在平面直角坐标系中,A(-1,-3),OB=,
OB与x轴所夹锐角是45°
(1)求B点坐标(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高。
例5(1)观察与发现:将矩形纸片AOCB折 ( http: / / www.21cnjy.com )叠,使点C与点A重合,点B落在点B′ 处(如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.
(2)实践与应用:以点O为坐标原点,分别以 ( http: / / www.21cnjy.com )矩形的边OC、OA为x轴、y轴建立如图2所示的直角坐标系,若顶点B的坐标为(9,3),请求出△AEF的面积和折痕EF的关系式.
二、课堂练习
1、在△ABC中,AB、BC、AC三边的长分别为、、,
(1)请在正方形网格中画出格点△ABC;(2)求出这个三角形BC边上的高.
2、在△ABC中,AB=13, AC=15,BC=5.求△ABC的面积.
3、如图,笔直的公路上A、 ( http: / / www.21cnjy.com )B两点相距10km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=8km,CB=3km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
4、如图,长方体的底面是边长为1cm 的正方形,高为3cm.
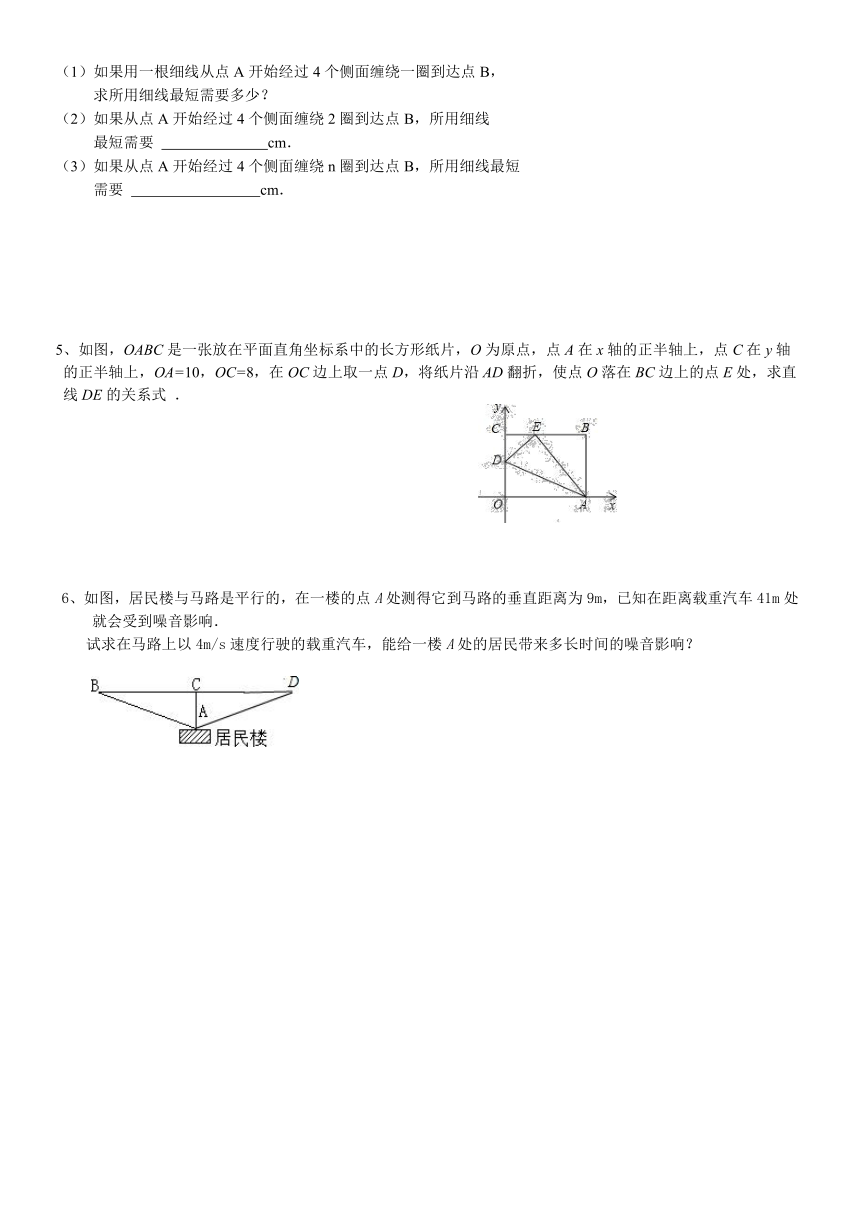
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,
求所用细线最短需要多少?
(2)如果从点A开始经过4个侧面缠绕2圈到达点B,所用细线
最短需要 cm.
(3)如果从点A开始经过4个侧面缠绕n圈到达点B,所用细线最短
需要 cm.
5、如图,OABC是一张放在平面直角坐 ( http: / / www.21cnjy.com )标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求直线DE的关系式 .
6、如图,居民楼与马路是平行的,在一楼的点A处测得它到马路的垂直距离为9m,已知在距离载重汽车41m处就会受到噪音影响.
试求在马路上以4m/s速度行驶的载重汽车,能给一楼A处的居民带来多长时间的噪音影响?
初二数学《勾股定理》、《实数》期末复习检测
班级 姓名
1.的平方根是 ;= ; ;= ;
2.当 时,有意义;
3. 已知一个直角三角形的两条边分别为6cm、8cm,这个直角三角形斜边上的高为 .
4.如果的整数部分为a,b是小数部分,那么a= .b= .
5.一个正数的两个平方根分别是2m-1和4-3m,则m= ,这个正数是
6.已知 点M(3,-1),点N( ( http: / / www.21cnjy.com )1,2),在y轴上找一点P,使得PM+PN的值最小,则点P的坐标是 ,PM+PN的最小值是 .
7.将13700米这个数精确到千位并用科学记数法表示为( )
A.1.37×104米 B. 1.4×104米 C.13.7×103米 D. 14×103米
8.下列实数中,、、、-3.14、、 、、0、 0.3232232223,无理数的个数是( ) A.2个 B.3个 C.4个 D.5个
9.若一个直角三角形的两边长分别为3和4,则它的第三边长为 ( )
A.5 B. C.5或4 D.5或
10. 计算与化简
(1) (2)若,求的值.
⑶已知x,y都是实数,且y=,试求xy的值.
(4) (x-1)2=25 (5) -8(2-x)3=27
11.如图,某学校(A点)与公路( ( http: / / www.21cnjy.com )直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
初二数学《勾股定理》、《实数》期末复习家作
班级 姓名
1. 的平方根是_______,的立方根是 .
2.的绝对值是 ;近似数万精确到_____________位.
3.若直角三角形斜边上的高和中线长分别是5 cm,8 cm,则它的面积是 cm2.
4.长方体的底面边长分别为1cm 和3cm, ( http: / / www.21cnjy.com )高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
5.用科学记数法把35989.76精确到百位表示为________。
6.已知正数的两个平方根是和,则= ;
7.如图,长方形ABCD中 ( http: / / www.21cnjy.com ),AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.
8.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,则图中实线所围成的图形面积S是 .
9.如图,已知AM⊥MN ( http: / / www.21cnjy.com ),BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点,若AM=3,BN=5,MN=15,则AC+BC= .
10.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
11. 如图,图中的所有三角形都是直 ( http: / / www.21cnjy.com )角三角形,所有四边形都是正方形,正方形A的边长为,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是 .
12.如图,有一个长方形的场院ABCD,其中
AB=9m,AD=12m,在B处竖直立着一根电线杆,
在电线杆上距地面8m的E处有一盏电灯.
点D到灯E的距离是
13.下列命题正确的个数有:(1) ( http: / / www.21cnjy.com ) ;(2) ;(3)无限小数都是无理数;(4)有限小数都是有理数;(5)实数分为正实数和负实数两类 ( )
A.1个 B.2个 C.3个 D.4个
14.如果下列各组数是三角形的三边长,那么不能组成直角三角形的一组 ( )
A. ,, B. 5, 12, 13 C.12,15,25 D. , ,1
15.在 中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
16.下列命题①如果a、b、c为一 ( http: / / www.21cnjy.com )组勾股数,那么4a、4b、4c仍是勾股数;②含有30°角的直角三角形的三边长之比是3:4:5;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1.其中正确的是( )
A.①② B.①④ C.①③ D.②④
17.(1)计算:
(2)解方程:① 8 ②
18.已知5x-1的算术平方根是3,4x+2y+1的立方根是1,求4x-2y平方根.
19.如图,小红用一张长方形纸片ABCD ( http: / / www.21cnjy.com )进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?
20.如图,在平面直角坐标系中有一矩 ( http: / / www.21cnjy.com )形ABCD,其中A(0,0),B (8,0),D (0,4),若将△ABC沿AC所在直线翻折,点B落在点E处.求E点的坐标。
A
B
A
第19题图
1cm
3cm
6cm
B
O
E
F
B′
图1
y
x
A
B
O
C
E
F
C
B′
图2
(命题人:吴晓玲 审核:初二数学组) 班级 姓名
一、重点题型
例1、如图,每个方格都是边长为1的正方形,
(1)求四边形ABCD的周长和面积;
(2)求∠ABC的度数,并说明理由。
例2、在△ABC中,AD是BC边上的高,若AB=l0,AD=8,AC=17,求△ABC的面积.
(画出示意图)
例3、如图是一个长、宽、高分别是4cm、 ( http: / / www.21cnjy.com )1cm和2cm的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,求它需要爬行的最短路径的长.
例4、已知如图,在平面直角坐标系中,A(-1,-3),OB=,
OB与x轴所夹锐角是45°
(1)求B点坐标(2)判断三角形ABO的形状
(3)求三角形ABO的AO边上的高。
例5(1)观察与发现:将矩形纸片AOCB折 ( http: / / www.21cnjy.com )叠,使点C与点A重合,点B落在点B′ 处(如图1),折痕为EF.小明发现△ AEF为等腰三角形,你同意吗?请说明理由.
(2)实践与应用:以点O为坐标原点,分别以 ( http: / / www.21cnjy.com )矩形的边OC、OA为x轴、y轴建立如图2所示的直角坐标系,若顶点B的坐标为(9,3),请求出△AEF的面积和折痕EF的关系式.
二、课堂练习
1、在△ABC中,AB、BC、AC三边的长分别为、、,
(1)请在正方形网格中画出格点△ABC;(2)求出这个三角形BC边上的高.
2、在△ABC中,AB=13, AC=15,BC=5.求△ABC的面积.
3、如图,笔直的公路上A、 ( http: / / www.21cnjy.com )B两点相距10km,C、D为两村庄,DA⊥AB于点A,CB⊥AB于点B,已知DA=8km,CB=3km,现在要在公路的AB段上建一个土特产品收购站E,使得C、D两村到收购站E的距离相等,则收购站E应建在离A点多远处?
4、如图,长方体的底面是边长为1cm 的正方形,高为3cm.
(1)如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,
求所用细线最短需要多少?
(2)如果从点A开始经过4个侧面缠绕2圈到达点B,所用细线
最短需要 cm.
(3)如果从点A开始经过4个侧面缠绕n圈到达点B,所用细线最短
需要 cm.
5、如图,OABC是一张放在平面直角坐 ( http: / / www.21cnjy.com )标系中的长方形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,使点O落在BC边上的点E处,求直线DE的关系式 .
6、如图,居民楼与马路是平行的,在一楼的点A处测得它到马路的垂直距离为9m,已知在距离载重汽车41m处就会受到噪音影响.
试求在马路上以4m/s速度行驶的载重汽车,能给一楼A处的居民带来多长时间的噪音影响?
初二数学《勾股定理》、《实数》期末复习检测
班级 姓名
1.的平方根是 ;= ; ;= ;
2.当 时,有意义;
3. 已知一个直角三角形的两条边分别为6cm、8cm,这个直角三角形斜边上的高为 .
4.如果的整数部分为a,b是小数部分,那么a= .b= .
5.一个正数的两个平方根分别是2m-1和4-3m,则m= ,这个正数是
6.已知 点M(3,-1),点N( ( http: / / www.21cnjy.com )1,2),在y轴上找一点P,使得PM+PN的值最小,则点P的坐标是 ,PM+PN的最小值是 .
7.将13700米这个数精确到千位并用科学记数法表示为( )
A.1.37×104米 B. 1.4×104米 C.13.7×103米 D. 14×103米
8.下列实数中,、、、-3.14、、 、、0、 0.3232232223,无理数的个数是( ) A.2个 B.3个 C.4个 D.5个
9.若一个直角三角形的两边长分别为3和4,则它的第三边长为 ( )
A.5 B. C.5或4 D.5或
10. 计算与化简
(1) (2)若,求的值.
⑶已知x,y都是实数,且y=,试求xy的值.
(4) (x-1)2=25 (5) -8(2-x)3=27
11.如图,某学校(A点)与公路( ( http: / / www.21cnjy.com )直线L)的距离为300米,又与公路车站(D点)的距离为500米,现要在公路上建一个小商店(C点),使之与该校A及车站D的距离相等,求商店与车站之间的距离.
初二数学《勾股定理》、《实数》期末复习家作
班级 姓名
1. 的平方根是_______,的立方根是 .
2.的绝对值是 ;近似数万精确到_____________位.
3.若直角三角形斜边上的高和中线长分别是5 cm,8 cm,则它的面积是 cm2.
4.长方体的底面边长分别为1cm 和3cm, ( http: / / www.21cnjy.com )高为6cm.如果用一根细线从点A开始经过4个侧面缠绕一圈到达点B,那么所用细线最短需要 cm.
5.用科学记数法把35989.76精确到百位表示为________。
6.已知正数的两个平方根是和,则= ;
7.如图,长方形ABCD中 ( http: / / www.21cnjy.com ),AD=10,AB=8,将长方形ABCD折叠,折痕为EF,点A的对应点A′落在线段BC上,当点A′ 在BC上移动时,点E、F也随之移动,若限定点E、F分别在线段AB、AD上移动,则点A′ 在线段BC上可移动的最大距离是___________.
8.如图,AE⊥AB,且AE=AB,BC⊥CD,且BC=CD,请按照图中所标注的数据,则图中实线所围成的图形面积S是 .
9.如图,已知AM⊥MN ( http: / / www.21cnjy.com ),BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点,若AM=3,BN=5,MN=15,则AC+BC= .
10.如图,将一根25㎝长的细木棒放入长、宽、高分别为8㎝、6㎝和㎝的长方体无盖盒子中,则细木棒露在盒外面的最短长度是 ㎝.
11. 如图,图中的所有三角形都是直 ( http: / / www.21cnjy.com )角三角形,所有四边形都是正方形,正方形A的边长为,另外四个正方形中的数字8,x,10,y分别表示该正方形面积,则x与y的数量关系是 .
12.如图,有一个长方形的场院ABCD,其中
AB=9m,AD=12m,在B处竖直立着一根电线杆,
在电线杆上距地面8m的E处有一盏电灯.
点D到灯E的距离是
13.下列命题正确的个数有:(1) ( http: / / www.21cnjy.com ) ;(2) ;(3)无限小数都是无理数;(4)有限小数都是有理数;(5)实数分为正实数和负实数两类 ( )
A.1个 B.2个 C.3个 D.4个
14.如果下列各组数是三角形的三边长,那么不能组成直角三角形的一组 ( )
A. ,, B. 5, 12, 13 C.12,15,25 D. , ,1
15.在 中,无理数有 ( )
A.1个 B.2个 C.3个 D.4个
16.下列命题①如果a、b、c为一 ( http: / / www.21cnjy.com )组勾股数,那么4a、4b、4c仍是勾股数;②含有30°角的直角三角形的三边长之比是3:4:5;③如果一个三角形的三边是12、25、21,那么此三角形必是直角三角形;④一个等腰直角三角形的三边是a、b、c,(a>b=c),那么a2∶b2∶c2=2∶1∶1.其中正确的是( )
A.①② B.①④ C.①③ D.②④
17.(1)计算:
(2)解方程:① 8 ②
18.已知5x-1的算术平方根是3,4x+2y+1的立方根是1,求4x-2y平方根.
19.如图,小红用一张长方形纸片ABCD ( http: / / www.21cnjy.com )进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?
20.如图,在平面直角坐标系中有一矩 ( http: / / www.21cnjy.com )形ABCD,其中A(0,0),B (8,0),D (0,4),若将△ABC沿AC所在直线翻折,点B落在点E处.求E点的坐标。
A
B
A
第19题图
1cm
3cm
6cm
B
O
E
F
B′
图1
y
x
A
B
O
C
E
F
C
B′
图2
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
