苏科版八年级数学上册第一章《全等三角形》复习教学设计
文档属性
| 名称 | 苏科版八年级数学上册第一章《全等三角形》复习教学设计 |

|
|
| 格式 | zip | ||
| 文件大小 | 88.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 00:00:00 | ||
图片预览

文档简介
第1章 全等三角形 复习 姓名
知识回顾:
1. 全等三角形的定义: .
2.全等三角形的性质: .
3.一般三角形全等的判别方法: .
直角三角形全等的判别方法:
4.三角形全等的条件思路:
当两三角形已具备两角对应相等时,第三条件应找 .
当两三角形已具备两边对应相等时,第三条件应找 .
当两三角形已具备一角一边对应相等时,第三条件应找 .
5.找三角形全等的条件时经常见到的隐含条件有: .
6.三个角对应相等的两个三角形全等吗?两 ( http: / / www.21cnjy.com )边和其中一边的对角对应相等的两个三角形全等吗?试举反例说明.
推陈出新:
一.挖掘“隐含条件”判全等
1.如图,AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由.
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= .说说理由.
二.添条件判全等
1.如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
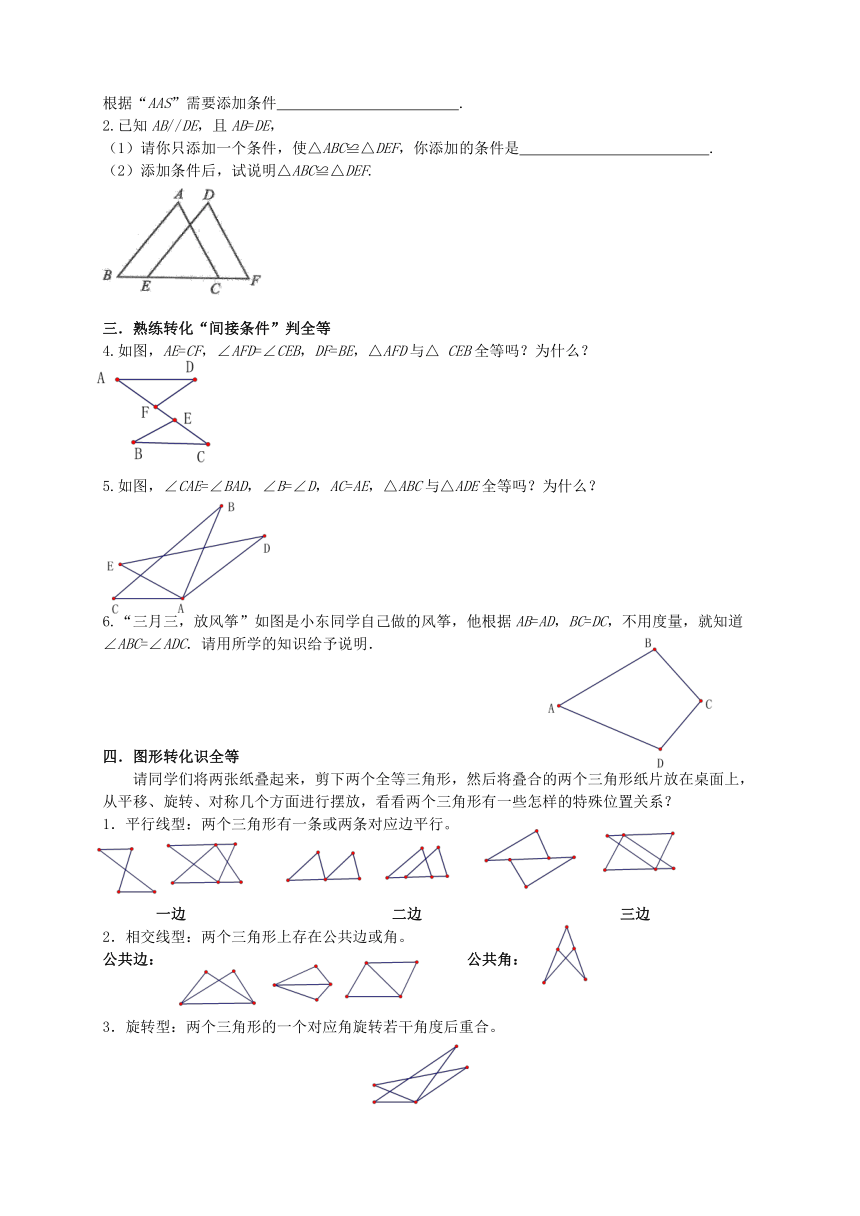
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是 .
(2)添加条件后,试说明△ABC≌△DEF.
三.熟练转化“间接条件”判全等
4.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
5.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
6.“三月三,放风筝”如图是小东同学自己做 ( http: / / www.21cnjy.com )的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.
四.图形转化识全等
请同学们将两张纸叠起来,剪下两个全等三角形 ( http: / / www.21cnjy.com ),然后将叠合的两个三角形纸片放在桌面上,从平移、旋转、对称几个方面进行摆放,看看两个三角形有一些怎样的特殊位置关系?
1.平行线型:两个三角形有一条或两条对应边平行。
一边 二边 三边
2.相交线型:两个三角形上存在公共边或角。
公共边: 公共角:
3.旋转型:两个三角形的一个对应角旋转若干角度后重合。
五.变式训练:
1.如图,AC=BD,∠CAB=∠DBA,试说明:BC=AD
变式1:如图,AC=BD,BC=AD,试说明:∠CAB=∠DBA
变式2:如图,AC=BD,∠C=∠D试说明:(1)AO=BO(2)CO=DO(3)BC=AD
课堂反馈:
1.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C. 说明:∠A=∠D
2.如图,已知AB=AD, ∠B=∠D,∠1=∠2,说明:BC=DE
3.(2006·攀枝花市) 如图,点E在AB上,AC=AD,请你添加一个
条件,使图中存在全等三角形,并给予证明.
所添条件为 ,
你得到的一对全等三角形是△ ≌△ .
课外作业:
1. 如图,点D,E分别在 ( http: / / www.21cnjy.com )线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是: .
2.如图,点B在AE上,∠CAB=∠D ( http: / / www.21cnjy.com )AB,要使△ABC≌△ABD,可补充的一个条件是: (写一个即可) .
3.工人师傅在安装木制门框时,为防 ( http: / / www.21cnjy.com )止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是根据三角形的
第1题 第2题 第3题 第4题
4.如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= .
5.如图,已知AB=DE,∠E=∠B,∠EFD=∠BCA,说明:AF=DC
6.等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)你能找到一对三角形的全等吗?并说明.
(2)BM,CN,MN之间有何关系?
若将直线l旋转到如下图的位置,其他条件不变,那么上题的结论是否依旧成立?
E
C
D
B
A
O
知识回顾:
1. 全等三角形的定义: .
2.全等三角形的性质: .
3.一般三角形全等的判别方法: .
直角三角形全等的判别方法:
4.三角形全等的条件思路:
当两三角形已具备两角对应相等时,第三条件应找 .
当两三角形已具备两边对应相等时,第三条件应找 .
当两三角形已具备一角一边对应相等时,第三条件应找 .
5.找三角形全等的条件时经常见到的隐含条件有: .
6.三个角对应相等的两个三角形全等吗?两 ( http: / / www.21cnjy.com )边和其中一边的对角对应相等的两个三角形全等吗?试举反例说明.
推陈出新:
一.挖掘“隐含条件”判全等
1.如图,AB=CD,AC=BD,则△ABC≌△DCB吗 说说理由.
2.如图(2),点D在AB上,点E在AC上,CD与BE相交于点O,且AD=AE,AB=AC.
若∠B=20°,CD=5cm,则∠C= ,BE= .说说理由.
3.如图(3),若OB=OD,∠A=∠C,若AB=3cm,则CD= .说说理由.
二.添条件判全等
1.如图,已知AD平分∠BAC,要使△ABD≌△ACD,
根据“SAS”需要添加条件 ;
根据“ASA”需要添加条件 ;
根据“AAS”需要添加条件 .
2.已知AB//DE,且AB=DE,
(1)请你只添加一个条件,使△ABC≌△DEF,你添加的条件是 .
(2)添加条件后,试说明△ABC≌△DEF.
三.熟练转化“间接条件”判全等
4.如图,AE=CF,∠AFD=∠CEB,DF=BE,△AFD与△ CEB全等吗?为什么?
5.如图,∠CAE=∠BAD,∠B=∠D,AC=AE,△ABC与△ADE全等吗?为什么?
6.“三月三,放风筝”如图是小东同学自己做 ( http: / / www.21cnjy.com )的风筝,他根据AB=AD,BC=DC,不用度量,就知道∠ABC=∠ADC.请用所学的知识给予说明.
四.图形转化识全等
请同学们将两张纸叠起来,剪下两个全等三角形 ( http: / / www.21cnjy.com ),然后将叠合的两个三角形纸片放在桌面上,从平移、旋转、对称几个方面进行摆放,看看两个三角形有一些怎样的特殊位置关系?
1.平行线型:两个三角形有一条或两条对应边平行。
一边 二边 三边
2.相交线型:两个三角形上存在公共边或角。
公共边: 公共角:
3.旋转型:两个三角形的一个对应角旋转若干角度后重合。
五.变式训练:
1.如图,AC=BD,∠CAB=∠DBA,试说明:BC=AD
变式1:如图,AC=BD,BC=AD,试说明:∠CAB=∠DBA
变式2:如图,AC=BD,∠C=∠D试说明:(1)AO=BO(2)CO=DO(3)BC=AD
课堂反馈:
1.如图,点E,F在BC上,BE=CF,AB=DC,∠B=∠C. 说明:∠A=∠D
2.如图,已知AB=AD, ∠B=∠D,∠1=∠2,说明:BC=DE
3.(2006·攀枝花市) 如图,点E在AB上,AC=AD,请你添加一个
条件,使图中存在全等三角形,并给予证明.
所添条件为 ,
你得到的一对全等三角形是△ ≌△ .
课外作业:
1. 如图,点D,E分别在 ( http: / / www.21cnjy.com )线段AB,AC上,BE,CD相交于点O,AE=AD,要使△ABE≌△ACD,需添加一个条件是: .
2.如图,点B在AE上,∠CAB=∠D ( http: / / www.21cnjy.com )AB,要使△ABC≌△ABD,可补充的一个条件是: (写一个即可) .
3.工人师傅在安装木制门框时,为防 ( http: / / www.21cnjy.com )止变形常常像图中所示,钉上两条斜拉的木条,这样做的原理是根据三角形的
第1题 第2题 第3题 第4题
4.如图,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD= .
5.如图,已知AB=DE,∠E=∠B,∠EFD=∠BCA,说明:AF=DC
6.等腰直角△ABC,其中AB=AC,∠BAC=90°,过B、C作经过A点直线L的垂线,垂足分别为M、N
(1)你能找到一对三角形的全等吗?并说明.
(2)BM,CN,MN之间有何关系?
若将直线l旋转到如下图的位置,其他条件不变,那么上题的结论是否依旧成立?
E
C
D
B
A
O
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
