苏科版八年级数学上册3.1《勾股定理》教学课件(共18张PPT)
文档属性
| 名称 | 苏科版八年级数学上册3.1《勾股定理》教学课件(共18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-11 00:00:00 | ||
图片预览


文档简介
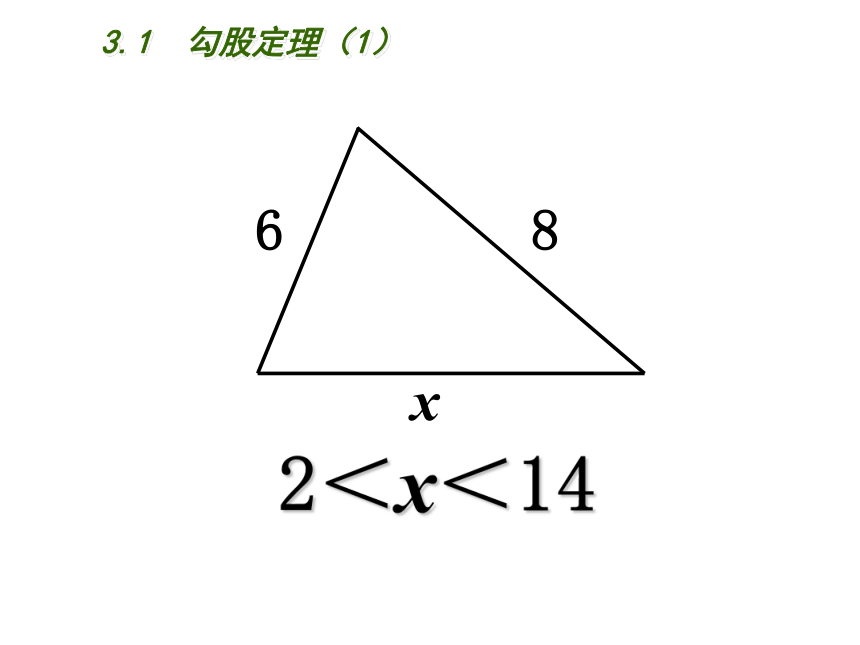
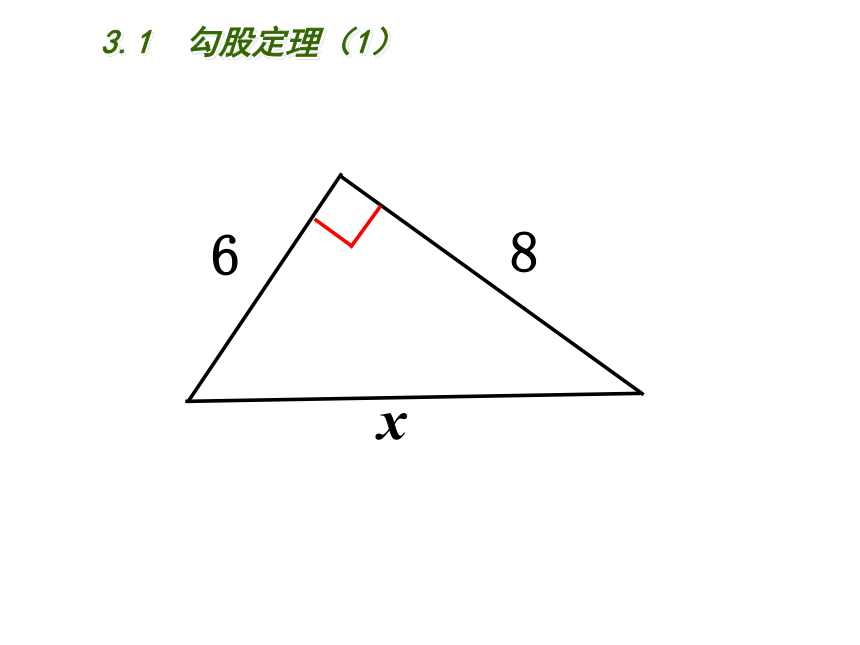
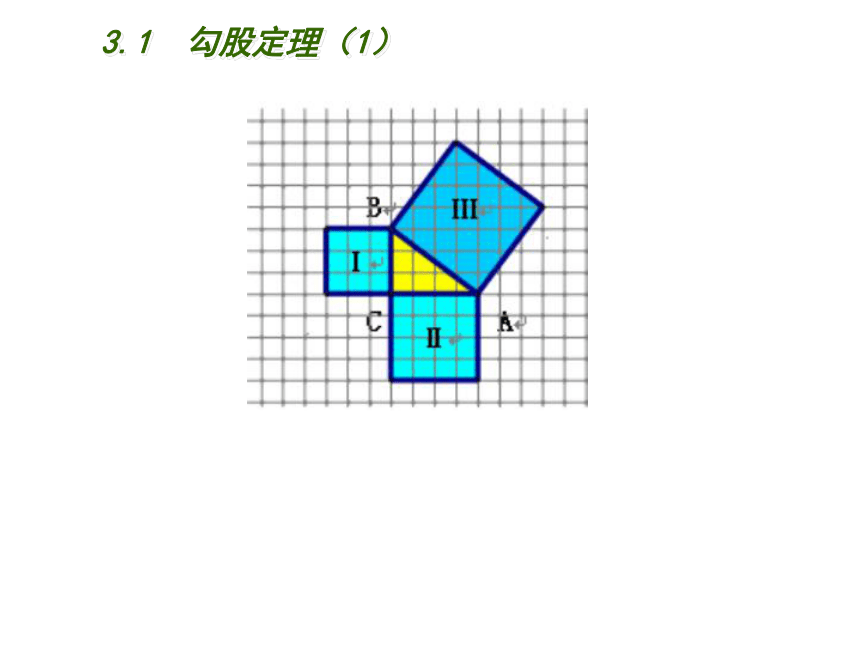
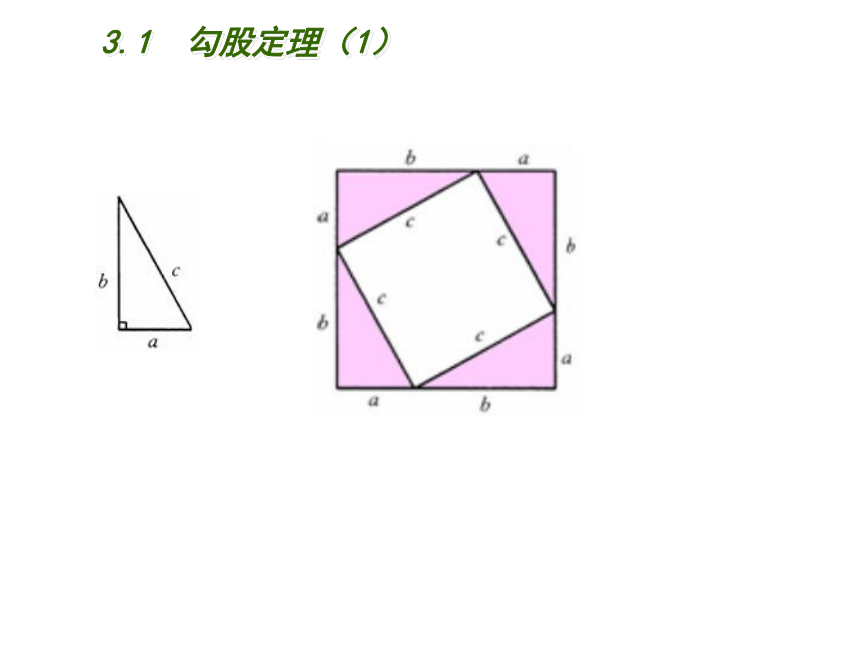
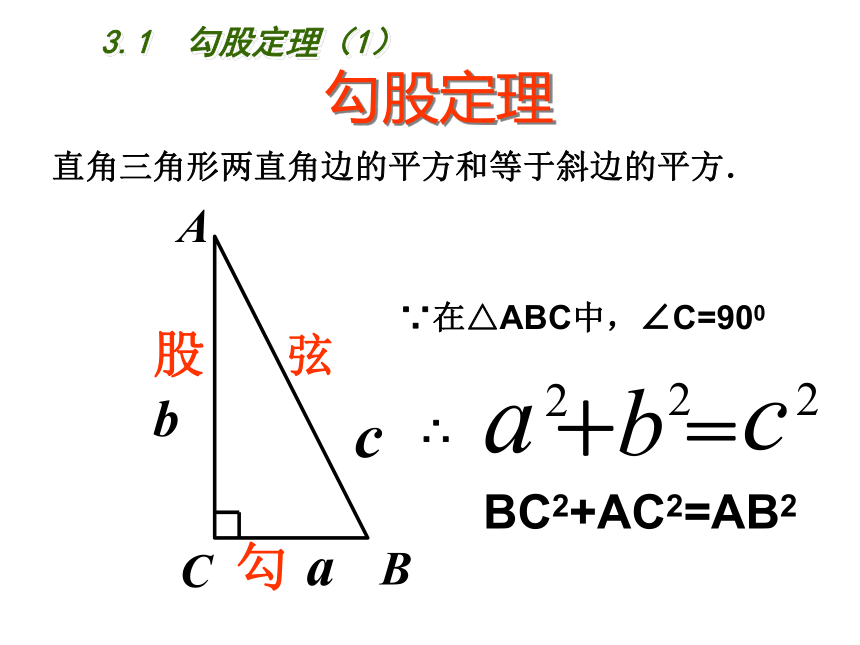
课件18张PPT。3.1 勾股定理八年级(上册)初中数学2<x<14x683.1 勾股定理(1)68x3.1 勾股定理(1) 勾股史话
我国是最早了解勾股定理的国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”.它被记载于我国古代著名的数学著作
《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.这一发现,至少早于古希腊人500多年.作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.3.1 勾股定理(1)3.1 勾股定理(1)3.1 勾股定理(1)勾股弦ABC3.1 勾股定理(1)∵在△ABC中,∠C=900BC2+AC2=AB23.1 勾股定理(2)勾股弦ABC3.1 勾股定理(1)∵在△ABC中,∠C=900BC2+AC2=AB21.求下列直角三角形中未知边的长:练一练3.1 勾股定理(1)2.求下列图中未知数x、y、z的值:3.1 勾股定理(1) 如图,一块长约 80m、宽约 60m 的长方形草坪,被一些人沿对角线踏出了一条“捷径”,类似的现象也时有发生.请问同学们:算一算1.走“捷径”的客观原因
是什么?为什么?2.“捷径”比正路近多少?3.1 勾股定理(1)巩固练习 如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
3.1 勾股定理(2) 一架消防队的梯子长25m,在一次火灾中, 梯子的底部离建筑物15m,此时,梯子最高能到多少米? 如果每层楼高4m,要想救上一层的人,梯子的底部要向楼的方向推进多少米?
CB3.1 勾股定理(1)
《九章算术》中的引葭(jiā) 赴岸问题:
??
“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.问水深和芦苇长各多少?3.1 勾股定理(1) 受台风格美影响,一棵树在离地面4米处断裂,
树的顶部落在离树跟底部3米处,这棵树折断前有多高?
3.1 勾股定理(1) 做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.3.1 勾股定理(1)谢 谢!
我国是最早了解勾股定理的国家之一.
早在三千多年前,周朝的数学家商高就提出,
将一根直尺折成一个直角,如果勾等于三,
股等于四,那么弦就等于五,即“勾三、股四、
弦五”.它被记载于我国古代著名的数学著作
《周髀算经》中.在这本书中的另一处,还记载了勾股定理的一般形式.这一发现,至少早于古希腊人500多年.作为一名中国人,我们应为我国古人的博学和多思而感到自豪!
勾股定理是人类文明的成果,几乎所有拥有古代文化的民族和国家都对勾股定理有所研究.在地球以外是否存在生命这个问题上,我国数学家华罗庚曾认为,如果外星人也拥有文明的话,我们可以用“勾股定理”的图形,作为人类探寻“外星人”并与“外星人”联系的“语言”.3.1 勾股定理(1)3.1 勾股定理(1)3.1 勾股定理(1)勾股弦ABC3.1 勾股定理(1)∵在△ABC中,∠C=900BC2+AC2=AB23.1 勾股定理(2)勾股弦ABC3.1 勾股定理(1)∵在△ABC中,∠C=900BC2+AC2=AB21.求下列直角三角形中未知边的长:练一练3.1 勾股定理(1)2.求下列图中未知数x、y、z的值:3.1 勾股定理(1) 如图,一块长约 80m、宽约 60m 的长方形草坪,被一些人沿对角线踏出了一条“捷径”,类似的现象也时有发生.请问同学们:算一算1.走“捷径”的客观原因
是什么?为什么?2.“捷径”比正路近多少?3.1 勾股定理(1)巩固练习 如图,长2.5m的梯子靠在墙上,梯子的底部离墙角1.5m,求梯子的顶端与地面的距离h.
3.1 勾股定理(2) 一架消防队的梯子长25m,在一次火灾中, 梯子的底部离建筑物15m,此时,梯子最高能到多少米? 如果每层楼高4m,要想救上一层的人,梯子的底部要向楼的方向推进多少米?
CB3.1 勾股定理(1)
《九章算术》中的引葭(jiā) 赴岸问题:
??
“今有池方一丈,葭(jiā)生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.”
题意是:有一个边长为10尺的正方形池塘,一棵芦苇AB生长在它的中央,高出水面部分BC为1尺.如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部B恰好碰到岸边的B′.问水深和芦苇长各多少?3.1 勾股定理(1) 受台风格美影响,一棵树在离地面4米处断裂,
树的顶部落在离树跟底部3米处,这棵树折断前有多高?
3.1 勾股定理(1) 做一个长、宽、高分别为50厘米、40厘米、30厘米的木箱,一根长为70厘米的木棒能否放入,为什么?试用今天学过的知识说明.3.1 勾股定理(1)谢 谢!
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
