苏科版八年级数学上册6.6《一次函数、一元一次方程和一元一次不等式》教学课件(共11张PPT)
文档属性
| 名称 | 苏科版八年级数学上册6.6《一次函数、一元一次方程和一元一次不等式》教学课件(共11张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 245.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-03-12 22:24:13 | ||
图片预览



文档简介
课件11张PPT。§6.6一次函数、
一元一次方程和一元一次不等式初中数学(苏科版)八年级(上册)一、复习引入1.已知一次函数y=2x+4
(1)当x = 0时,求y 的值;
(2)当y = 0时,求x的值;
(3)当y > 0时,求x的取值范围.
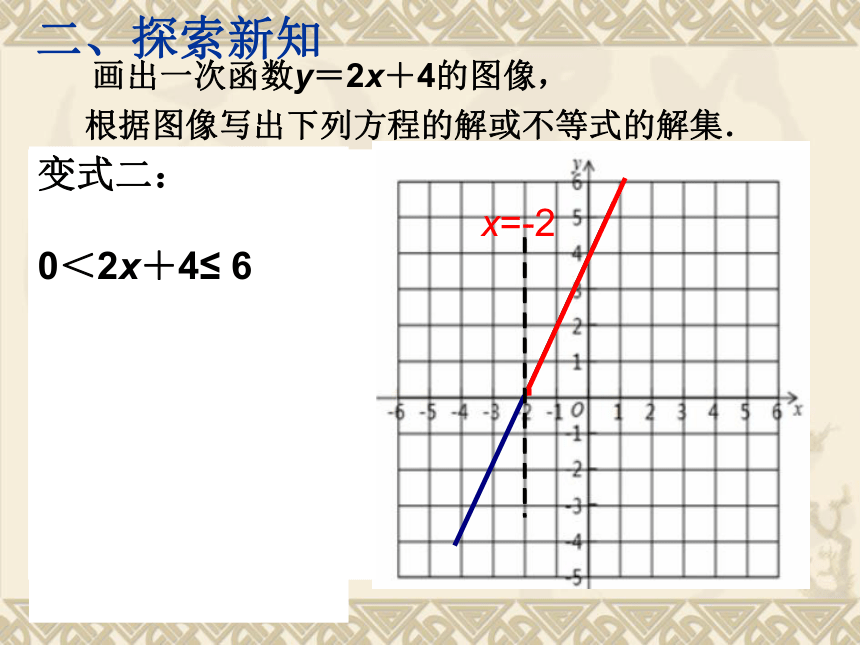
画出一次函数y=2x+4的图像,
根据图像写出下列方程的解或不等式的解集.
(1)2x+4=0
(2)2x+4> 0
(3)2x+4≤ 0·x=-2x>-2X≤-2变式一:
(1)2x+4=6
(2)2x+4> 6
(3)2x+4≤ 6
变式二:
0<2x+4≤ 6
二、探索新知已知一次函数的表达式
归纳总结 一次函数、一元一次方程、一元一次不等式有着紧密的联系.
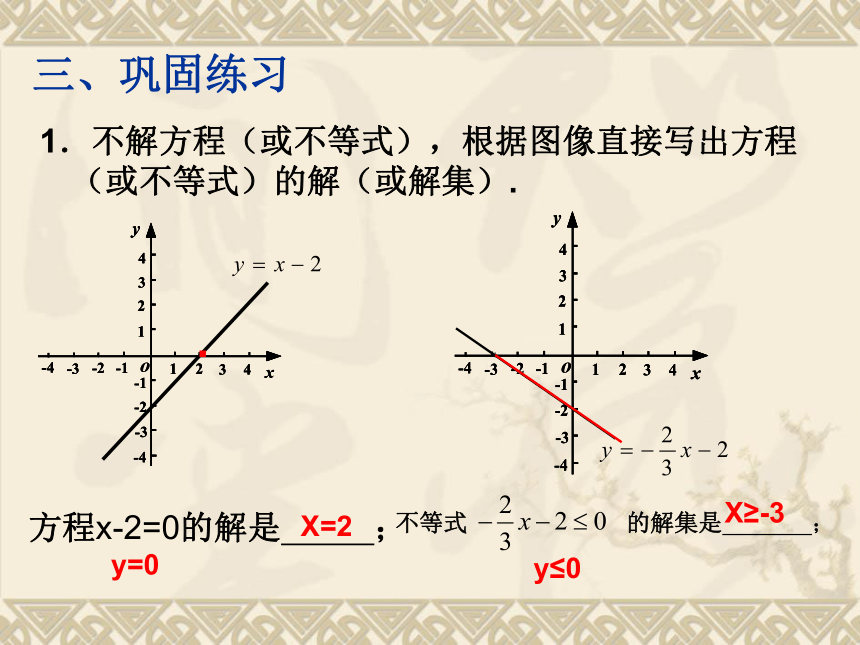
当其中一个变量的值确定时,可以由相应的一元一次方程确定另一个变量的值;当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.蕴含的数学思想是转化思想与数形结合思想三、巩固练习1.不解方程(或不等式),根据图像直接写出方程(或不等式)的解(或解集).方程x-2=0的解是 ; 不等式 的解集是 ; X=2X≥-3·y=0y≤0X≤2(2,3)y≥32.不解方程组(或不等式),根据图像直接写出方程组(或不等式)的解(或解集). (1)方程组
的解是 ;(2)不等式
的解集是 ;X>-3(-3,2)y1<y2四、例题讲解例 一根长20cm的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm.设所挂物体的质量为x kg,弹簧的长度为y cm.(1)写出y与x之间的函数表达式;(3)求这根弹簧在所允许的限度内所挂物体的最大质量.①当弹簧的长度为 cm时,所挂物体的质量最大; 分析35②题目中的“不超过”其实暗含的是 的模型,
所以可以考虑用 解决问题; ③画出函数图像,可以直观的看出弹簧伸长与所挂物体的质量之间的关系. 现在你能确定自变量的取值范围吗? (2)有一物体的质量是30 kg ,能挂在这根弹簧上吗?四、例题讲解例 一根长20cm的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm.设所挂物体的质量为x kg,弹簧的长度为y cm.
(4)若所挂物体质量不少于10kg而不大于15kg,
请确定挂上物体后弹簧的长度范围.五、拓展提升 一辆汽车行驶了35 km后,驶入高速公路,并以105 km/h的速度匀速行驶了x h.试根据上述情境,提出一些问题,并用一次函数、一元一次方程或一元一次不等式求解.问题1:设汽车行驶的总路程为y km,写出y与x之间的函数关系式.问题2:当汽车在高速公路行驶了2 h时,汽车共行驶了多少km?问题3:司机根据地图估计从出发地到下高速路口至少350km,那么汽车至少在高速公路上行驶多长时间?……六、课堂小结1.函数、方程、不等式都是刻画现实世界中量与量之间变化过程的重要模型,三者之间相互联系;
2.函数求值和变量范围确定的问题可以通过方程、不等式解决,体现了转化的数学思想;
3. 与方程、不等式有关的数量关系与大小比较的问题,也可以通过函数图像加以分析,体现了数形结合的数学思想. 数缺形时少知觉,形少数时难入微,
数形结合百般好,割裂分家万事休.----华罗庚
(1)当x = 0时,求y 的值;
(2)当y = 0时,求x的值;
(3)当y > 0时,求x的取值范围.
画出一次函数y=2x+4的图像,
根据图像写出下列方程的解或不等式的解集.
(1)2x+4=0
(2)2x+4> 0
(3)2x+4≤ 0·x=-2x>-2X≤-2变式一:
(1)2x+4=6
(2)2x+4> 6
(3)2x+4≤ 6
变式二:
0<2x+4≤ 6
二、探索新知已知一次函数的表达式
归纳总结 一次函数、一元一次方程、一元一次不等式有着紧密的联系.
当其中一个变量的值确定时,可以由相应的一元一次方程确定另一个变量的值;当其中一个变量的取值范围确定时,可以由相应的一元一次不等式确定另一个变量的取值范围.蕴含的数学思想是转化思想与数形结合思想三、巩固练习1.不解方程(或不等式),根据图像直接写出方程(或不等式)的解(或解集).方程x-2=0的解是 ; 不等式 的解集是 ; X=2X≥-3·y=0y≤0X≤2(2,3)y≥32.不解方程组(或不等式),根据图像直接写出方程组(或不等式)的解(或解集). (1)方程组
的解是 ;(2)不等式
的解集是 ;X>-3(-3,2)y1<y2四、例题讲解例 一根长20cm的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm.设所挂物体的质量为x kg,弹簧的长度为y cm.(1)写出y与x之间的函数表达式;(3)求这根弹簧在所允许的限度内所挂物体的最大质量.①当弹簧的长度为 cm时,所挂物体的质量最大; 分析35②题目中的“不超过”其实暗含的是 的模型,
所以可以考虑用 解决问题; ③画出函数图像,可以直观的看出弹簧伸长与所挂物体的质量之间的关系. 现在你能确定自变量的取值范围吗? (2)有一物体的质量是30 kg ,能挂在这根弹簧上吗?四、例题讲解例 一根长20cm的弹簧,一端固定,另一端挂物体.在弹簧伸长后的长度不超过30cm的限度内,每挂1kg质量的物体,弹簧伸长0.5cm.设所挂物体的质量为x kg,弹簧的长度为y cm.
(4)若所挂物体质量不少于10kg而不大于15kg,
请确定挂上物体后弹簧的长度范围.五、拓展提升 一辆汽车行驶了35 km后,驶入高速公路,并以105 km/h的速度匀速行驶了x h.试根据上述情境,提出一些问题,并用一次函数、一元一次方程或一元一次不等式求解.问题1:设汽车行驶的总路程为y km,写出y与x之间的函数关系式.问题2:当汽车在高速公路行驶了2 h时,汽车共行驶了多少km?问题3:司机根据地图估计从出发地到下高速路口至少350km,那么汽车至少在高速公路上行驶多长时间?……六、课堂小结1.函数、方程、不等式都是刻画现实世界中量与量之间变化过程的重要模型,三者之间相互联系;
2.函数求值和变量范围确定的问题可以通过方程、不等式解决,体现了转化的数学思想;
3. 与方程、不等式有关的数量关系与大小比较的问题,也可以通过函数图像加以分析,体现了数形结合的数学思想. 数缺形时少知觉,形少数时难入微,
数形结合百般好,割裂分家万事休.----华罗庚
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
