湖北省武汉外校2024-2025学年八年级上学期期中数学考试题(word版,无答案)
文档属性
| 名称 | 湖北省武汉外校2024-2025学年八年级上学期期中数学考试题(word版,无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 21:15:23 | ||
图片预览

文档简介
2024—2025学年上学期
武汉外国语学校八年级期中考试
数 学试 卷
试卷满分:120分 考试时间:120分钟
一、选择题(每小题3分,共计30分)
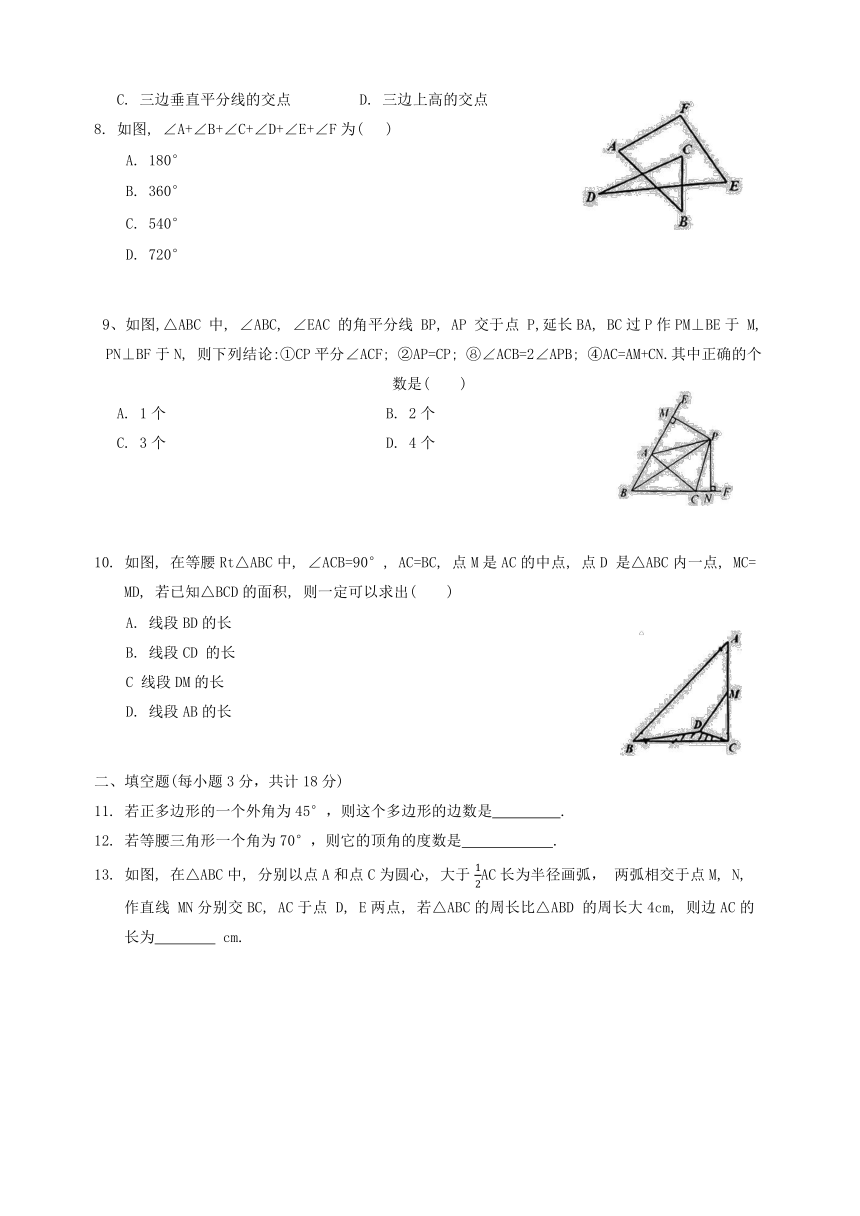
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性. 下列汉字是轴对称图形的是( )
2. 已知三角形的两边的长分别为8,3,第三边的长可能是( )
A. 3 B. 4 C. 9 D. 12
3. 如图,在△ABC中,关于高的说法正确的是( )
A. 线段AD是AB边上的高 B. 线段BE是AC边上的高
C. 线段CF是AC边上的高 D. 线段CF是 BC边上的高
4. 如图所示,为了测量水池两边A,B间的距离,可以先过点A作射线AE,再过B点作BD⊥AE于D, 在AD 延长线上截取DC=AD, 连接BC, 则 BC的长就是A, B间的距离,用来判定△ABD≌△CBD 的理由是( )
A. HL B. SAS C. ASA D. AAS
5. 已知点A(a,2)与点B(3,b)关于x轴对称, 则a+2b= ( )
A. - 4 B. - 1 C. - 2 D. 4
6. 如图,已知∠1=∠2, 则下列条件中,不能使△ABC≌△DCB 成立的是( )
A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
7. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边垂直平分线的交点 D. 三边上高的交点
8. 如图, ∠A+∠B+∠C+∠D+∠E+∠F为( )
A. 180°
B. 360°
C. 540°
D. 720°
9、如图,△ABC 中, ∠ABC, ∠EAC 的角平分线 BP, AP 交于点 P,延长BA, BC过P作PM⊥BE于 M, PN⊥BF于N, 则下列结论:①CP平分∠ACF; ②AP=CP; ⑧∠ACB=2∠APB; ④AC=AM+CN.其中正确的个数是( )
A. 1个 B. 2个
C. 3个 D. 4个
10. 如图, 在等腰Rt△ABC中, ∠ACB=90°, AC=BC, 点M是AC的中点, 点D 是△ABC内一点, MC=MD, 若已知△BCD的面积, 则一定可以求出( )
A. 线段BD的长
B. 线段CD 的长
C 线段DM的长
D. 线段AB的长
二、填空题(每小题3分,共计18分)
11. 若正多边形的一个外角为45°,则这个多边形的边数是 .
12. 若等腰三角形一个角为70°,则它的顶角的度数是 .
13. 如图, 在△ABC中, 分别以点A和点C为圆心, 大于 AC长为半径画弧, 两弧相交于点M, N, 作直线 MN分别交BC, AC于点 D, E两点, 若△ABC的周长比△ABD 的周长大4cm, 则边AC的长为 cm.
14. 如图①, ②, ∠A=α, ∠1=∠2, ∠3=∠4, 则∠M+∠P 的度数为 .
15. 如图, 在△ABC 中 AB=AC, AD⊥BC 于点 D, 点 E 为 AD 上一点, ∠ABE=∠CBE,若△ABC的面积是12, AC+CD=8, 则DE的长是 .
16. 如图, 在等腰△ABC中, 顶角∠B=42°, 点 D为AC边上一定点,E, F分别为边 AB 和BC上两动点,且EF∥AC,当DE+DF的值最小时, ∠EDF 的大小是 .
三、解答题 (本题共计72分)
17. (本题8分)已知等腰△ABC的周长为18,一边长为4,求另两边的长.
18.(本题8分)如图, 点B, E, C, F在同一条直线上, AB=DE, AC=DF, BE=CF.求证: AB∥DE.
19. (本题 8 分)如图, △ABC中, AB=8, AC=6, BC=7, AD 平分∠BAC交BC于D, 点E为AB边上一点, AE=AC.
(1) 求证: △ADE≌△ADC;
(2) △BDE的周长是 .
20.(本题8分)如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.
(1) 求证: ∠ACD=∠BEC;
(2)若点F为DE上一点,CF平分∠DCE,则∠CFD的度数是 .
21. (本题8分)如图是由小正方形组成的7×6网格,每个小正方形的顶点叫做格点. △ABC的三个顶点都是格点.仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示.
(1)在图1中,先画格点F,使得BF∥AC,画出线段BF,再在线段AF上画点O,使得CO=AB.
(2) 在图2中,点D 是边AC与网格线的交点,先画点C关于AB的对称点E,再在AB上画点 P, 使∠APD=∠BPC;
22. (本题10分) (1)如图1,在等腰Rt△ACB与等腰Rt△MCN中,若AC=BC, MC=NC,∠ACB=∠MCN=90°. 求证: △ACM≌△BCN;
(2)在等腰Rt△ACB中, ∠ACB=90°, AC=BC, D为BC边上一点, E为射线AD上一点,连接BE, CE, ∠CED=45°.
①如图2, 点E在AD的延长线上, 求证: BE⊥AE;
②如图3, 点E在AD上, 若∠BED=30°, 则 的值是 .
23. (本题10分)当条件中出现“中线”或“中点”时,可考虑倍长中线或作一条边的平行线来解决问题.
【小试牛刀】
(1) 如图1,在△ABC中, AB=6, AC=4, 则BC边上的中线AD的取值范围是 ;
【尝试运用】
(2) 如图2, AB∥CE, 点D为BC中点, 点F在DA 的延长线上, ∠DAB=∠F, 若AB=8,CE=2, 求EF的长;
【拓展延伸】
(3)如图3, 在△ABC中, AD是中线, 点E是AD上一点, BE=AC, AE=BD, 若∠CAD=α,则∠DBE的大小是 (用含α的式子表示) .
24. (本题12分)在平面直角坐标系中,点A(a,0),点B(0,b),且a,b满足 点R(0,t)是y轴上一动点,将线段AR绕点 R顺时针旋转90°得线段CR.
(1) 如图1, 若t=1, 则点C 的坐标是 ;
(2) 过点B作BD∥OA, 交直线AC于点D, 连接RD.
①如图2, 若t>0, 求证: ∠CAO=∠ADR;
②如图3, 若t=-1, 求DR-DB的值.
武汉外国语学校八年级期中考试
数 学试 卷
试卷满分:120分 考试时间:120分钟
一、选择题(每小题3分,共计30分)
1. 现实世界中,对称现象无处不在,中国的方块字中有些也具有对称性. 下列汉字是轴对称图形的是( )
2. 已知三角形的两边的长分别为8,3,第三边的长可能是( )
A. 3 B. 4 C. 9 D. 12
3. 如图,在△ABC中,关于高的说法正确的是( )
A. 线段AD是AB边上的高 B. 线段BE是AC边上的高
C. 线段CF是AC边上的高 D. 线段CF是 BC边上的高
4. 如图所示,为了测量水池两边A,B间的距离,可以先过点A作射线AE,再过B点作BD⊥AE于D, 在AD 延长线上截取DC=AD, 连接BC, 则 BC的长就是A, B间的距离,用来判定△ABD≌△CBD 的理由是( )
A. HL B. SAS C. ASA D. AAS
5. 已知点A(a,2)与点B(3,b)关于x轴对称, 则a+2b= ( )
A. - 4 B. - 1 C. - 2 D. 4
6. 如图,已知∠1=∠2, 则下列条件中,不能使△ABC≌△DCB 成立的是( )
A. AB=CD B. AC=BD C. ∠A=∠D D. ∠ABC=∠DCB
7. 在联欢会上,有A,B,C三名选手站在一个三角形的三个顶点位置上,他们在玩抢凳子游戏,要求在他们中间放一个木凳,谁先抢到凳子谁获胜,为使游戏公平,则凳子应放的最适当的位置是在△ABC的( )
A. 三边中线的交点 B. 三条角平分线的交点
C. 三边垂直平分线的交点 D. 三边上高的交点
8. 如图, ∠A+∠B+∠C+∠D+∠E+∠F为( )
A. 180°
B. 360°
C. 540°
D. 720°
9、如图,△ABC 中, ∠ABC, ∠EAC 的角平分线 BP, AP 交于点 P,延长BA, BC过P作PM⊥BE于 M, PN⊥BF于N, 则下列结论:①CP平分∠ACF; ②AP=CP; ⑧∠ACB=2∠APB; ④AC=AM+CN.其中正确的个数是( )
A. 1个 B. 2个
C. 3个 D. 4个
10. 如图, 在等腰Rt△ABC中, ∠ACB=90°, AC=BC, 点M是AC的中点, 点D 是△ABC内一点, MC=MD, 若已知△BCD的面积, 则一定可以求出( )
A. 线段BD的长
B. 线段CD 的长
C 线段DM的长
D. 线段AB的长
二、填空题(每小题3分,共计18分)
11. 若正多边形的一个外角为45°,则这个多边形的边数是 .
12. 若等腰三角形一个角为70°,则它的顶角的度数是 .
13. 如图, 在△ABC中, 分别以点A和点C为圆心, 大于 AC长为半径画弧, 两弧相交于点M, N, 作直线 MN分别交BC, AC于点 D, E两点, 若△ABC的周长比△ABD 的周长大4cm, 则边AC的长为 cm.
14. 如图①, ②, ∠A=α, ∠1=∠2, ∠3=∠4, 则∠M+∠P 的度数为 .
15. 如图, 在△ABC 中 AB=AC, AD⊥BC 于点 D, 点 E 为 AD 上一点, ∠ABE=∠CBE,若△ABC的面积是12, AC+CD=8, 则DE的长是 .
16. 如图, 在等腰△ABC中, 顶角∠B=42°, 点 D为AC边上一定点,E, F分别为边 AB 和BC上两动点,且EF∥AC,当DE+DF的值最小时, ∠EDF 的大小是 .
三、解答题 (本题共计72分)
17. (本题8分)已知等腰△ABC的周长为18,一边长为4,求另两边的长.
18.(本题8分)如图, 点B, E, C, F在同一条直线上, AB=DE, AC=DF, BE=CF.求证: AB∥DE.
19. (本题 8 分)如图, △ABC中, AB=8, AC=6, BC=7, AD 平分∠BAC交BC于D, 点E为AB边上一点, AE=AC.
(1) 求证: △ADE≌△ADC;
(2) △BDE的周长是 .
20.(本题8分)如图,点C在线段AB上,AD∥EB,AC=BE,AD=BC.
(1) 求证: ∠ACD=∠BEC;
(2)若点F为DE上一点,CF平分∠DCE,则∠CFD的度数是 .
21. (本题8分)如图是由小正方形组成的7×6网格,每个小正方形的顶点叫做格点. △ABC的三个顶点都是格点.仅用无刻度的直尺在给定的网格中完成画图,画图过程用虚线表示.
(1)在图1中,先画格点F,使得BF∥AC,画出线段BF,再在线段AF上画点O,使得CO=AB.
(2) 在图2中,点D 是边AC与网格线的交点,先画点C关于AB的对称点E,再在AB上画点 P, 使∠APD=∠BPC;
22. (本题10分) (1)如图1,在等腰Rt△ACB与等腰Rt△MCN中,若AC=BC, MC=NC,∠ACB=∠MCN=90°. 求证: △ACM≌△BCN;
(2)在等腰Rt△ACB中, ∠ACB=90°, AC=BC, D为BC边上一点, E为射线AD上一点,连接BE, CE, ∠CED=45°.
①如图2, 点E在AD的延长线上, 求证: BE⊥AE;
②如图3, 点E在AD上, 若∠BED=30°, 则 的值是 .
23. (本题10分)当条件中出现“中线”或“中点”时,可考虑倍长中线或作一条边的平行线来解决问题.
【小试牛刀】
(1) 如图1,在△ABC中, AB=6, AC=4, 则BC边上的中线AD的取值范围是 ;
【尝试运用】
(2) 如图2, AB∥CE, 点D为BC中点, 点F在DA 的延长线上, ∠DAB=∠F, 若AB=8,CE=2, 求EF的长;
【拓展延伸】
(3)如图3, 在△ABC中, AD是中线, 点E是AD上一点, BE=AC, AE=BD, 若∠CAD=α,则∠DBE的大小是 (用含α的式子表示) .
24. (本题12分)在平面直角坐标系中,点A(a,0),点B(0,b),且a,b满足 点R(0,t)是y轴上一动点,将线段AR绕点 R顺时针旋转90°得线段CR.
(1) 如图1, 若t=1, 则点C 的坐标是 ;
(2) 过点B作BD∥OA, 交直线AC于点D, 连接RD.
①如图2, 若t>0, 求证: ∠CAO=∠ADR;
②如图3, 若t=-1, 求DR-DB的值.
同课章节目录
