人教版2024-2025学年八年级数学上册《第十一章 三角形》单元测试题(含解析)
文档属性
| 名称 | 人教版2024-2025学年八年级数学上册《第十一章 三角形》单元测试题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 450.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
2024-2025学年八年级数学上册《第十一章 三角形》单元测试题 人教版
一、选择题(共10题;共30分)
1.(3分)下列长度(单位cm)的线段不能组成三角形的是( )
A.3,3,3 B.3,5,5 C.3,4,5 D.3,5,8
2.(3分)如图,的面积为18,为的中线,E、F为的两个三等分点,连接,则图中阴影部分的面积和为( )
A.4 B.6 C.8 D.9
3.(3分)下列图形具有稳定性的是( )
A. B.
C. D.
4.(3分)在△ABC中,∠A=60°,∠B=40°,则∠C等于( ).
A.100° B.80° C.60° D.40°
5.(3分)在△ABC中,∠A,∠B,∠C的度数之比为3:4:5,那么△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
6.(3分)如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
7.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95° C.85° D.75°
8.(3分)一个正多边形的每一个内角是 ,则从这个正多边形的一个顶点出发可作( )条对角线.
A.5 B.4 C.3 D.2
9.(3分)若一个多边形的对角线条数恰好为边数的2倍,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
10.(3分)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90° B.135° C.270° D.315°
二、填空题(共8题;共24分)
11.(3分)一个三角形的两边长为5和7,则第三边a的取值范围是 .
12.(3分)如图,AD是△ABC的角平分线,AB=6,AC=4,则△ABD与△ACD的面积之比为 .
13.(3分)如图,手机支架采用了三角形结构,这样设计依据的数学道理是三角形具有 性.
14.(3分)如图, °.
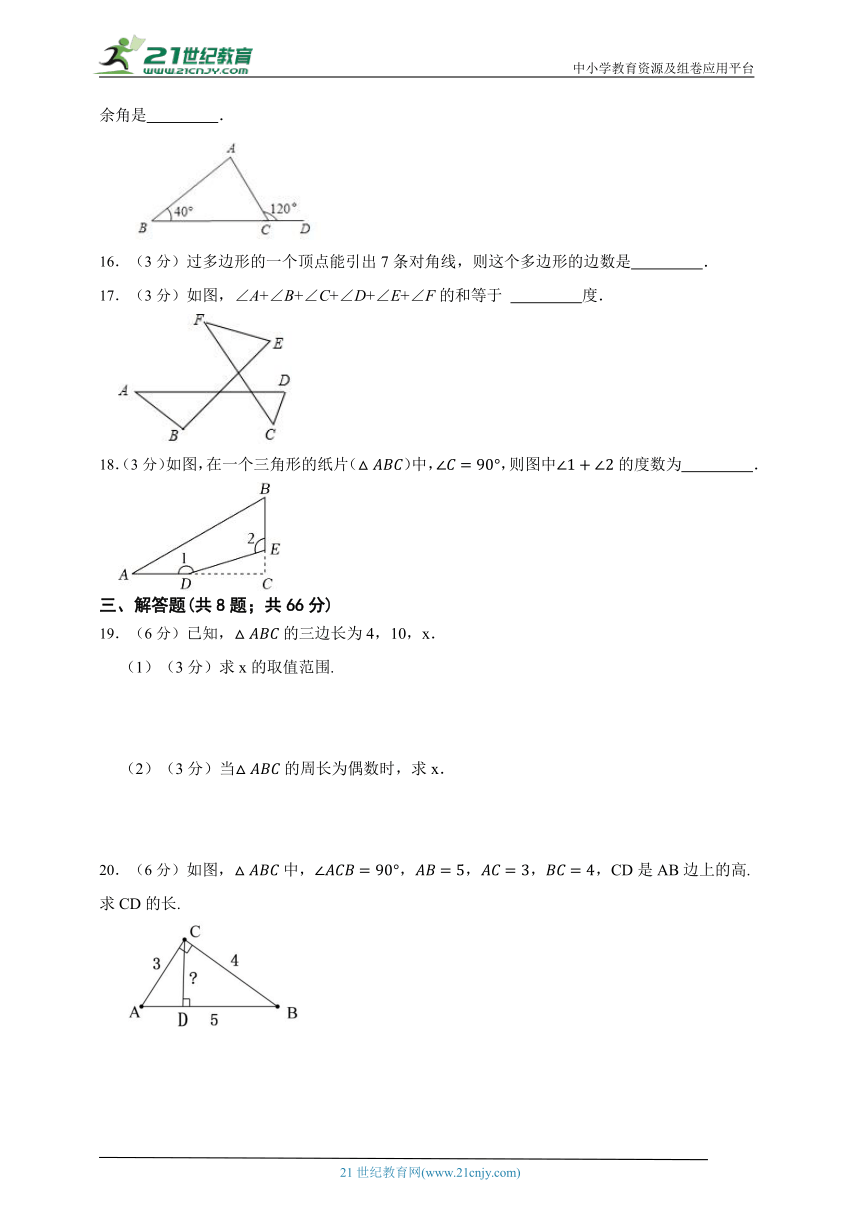
15.(3分)如图,在△ABC中,点D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A的余角是 .
16.(3分)过多边形的一个顶点能引出7条对角线,则这个多边形的边数是 .
17.(3分)如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于 度.
18.(3分)如图,在一个三角形的纸片()中,,则图中的度数为 .
三、解答题(共8题;共66分)
19.(6分)已知,的三边长为4,10,x.
(1)(3分)求x的取值范围.
(2)(3分)当的周长为偶数时,求x.
20.(6分)如图,中,,,,,CD是AB边上的高.求CD的长.
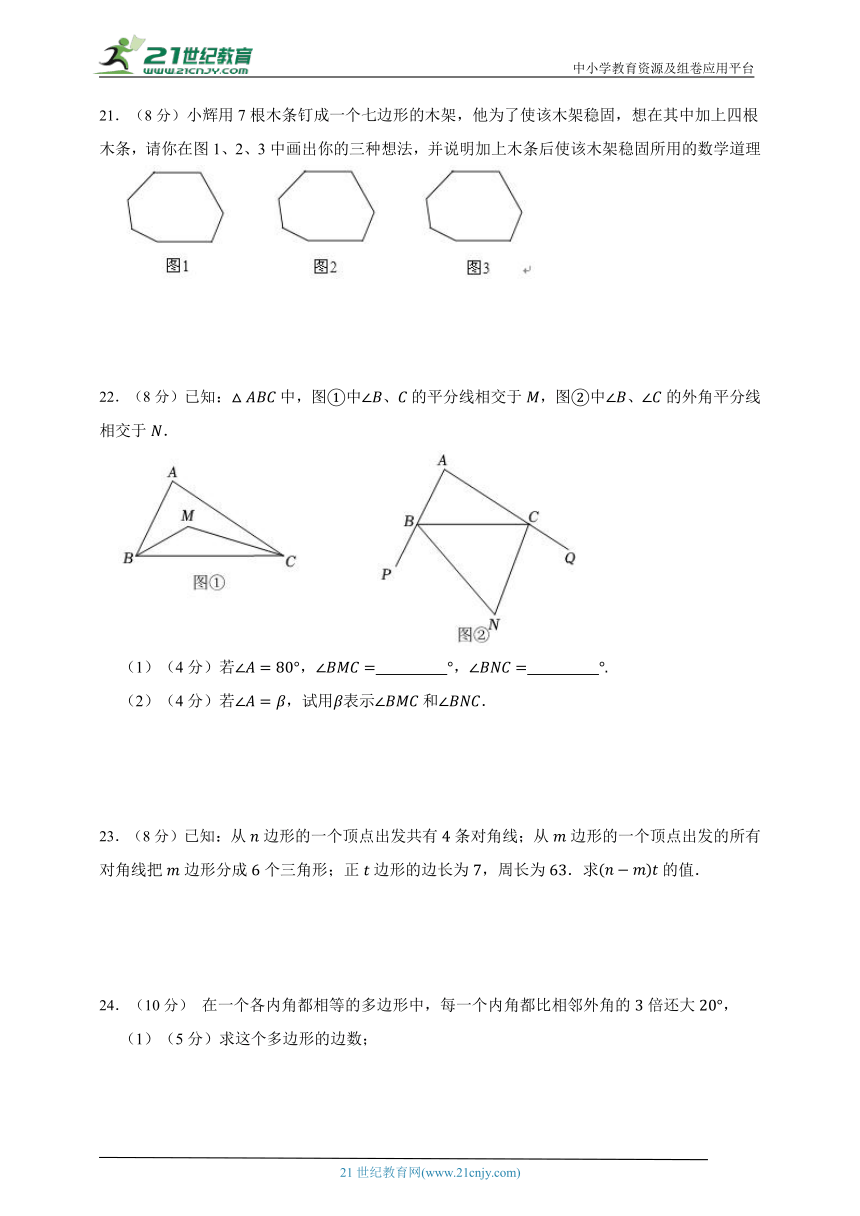
21.(8分)小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理
22.(8分)已知:中,图中、的平分线相交于,图中、的外角平分线相交于.
(1)(4分)若, ,
(2)(4分)若,试用表示和.
23.(8分)已知:从边形的一个顶点出发共有条对角线;从边形的一个顶点出发的所有对角线把边形分成个三角形;正边形的边长为,周长为.求的值.
24.(10分) 在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大,
(1)(5分)求这个多边形的边数;
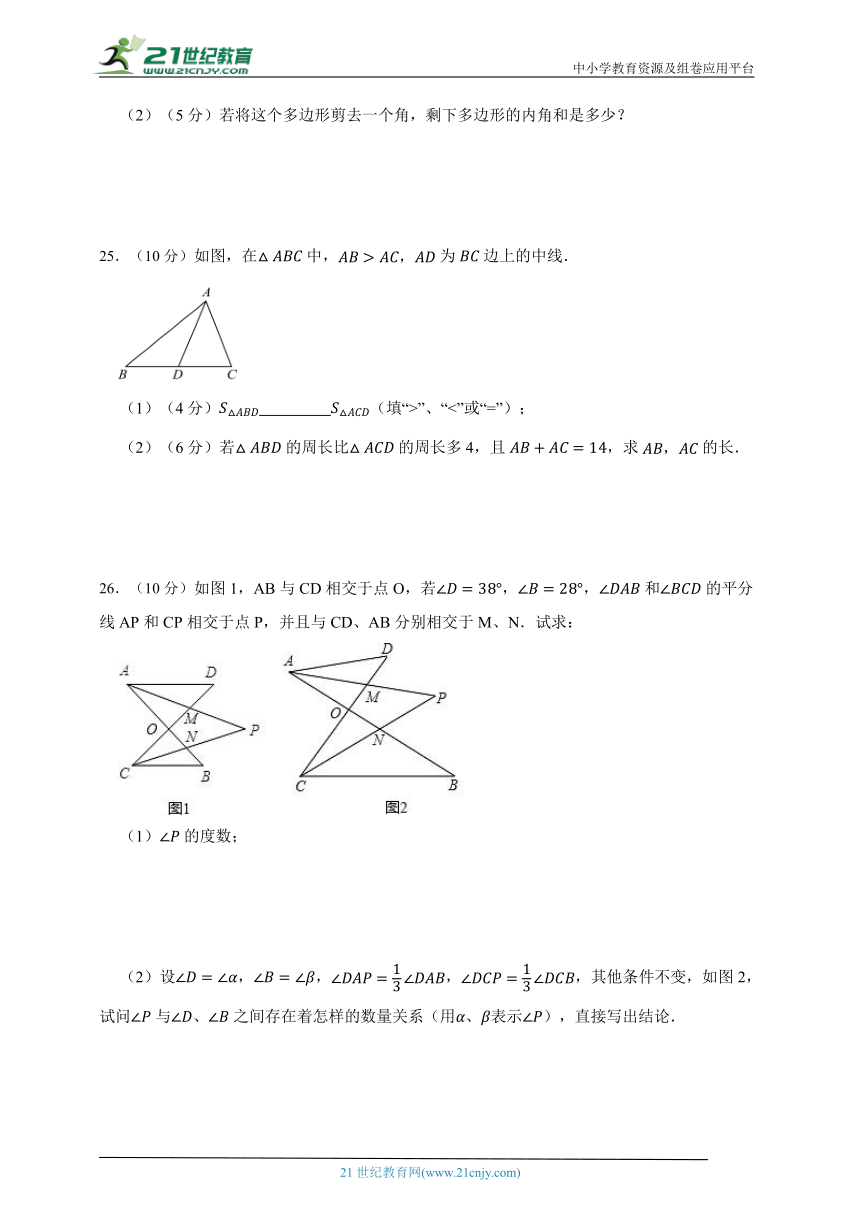
(2)(5分)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
25.(10分)如图,在中,为边上的中线.
(1)(4分) (填“>”、“<”或“=”);
(2)(6分)若的周长比的周长多4,且,求的长.
26.(10分)如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
答案解析部分
1.【答案】D
【知识点】三角形三边关系
【解析】【解答】解:A、∵3+3>3,∴能组成三角形,故A不符合题意;
B、∵3+5>5,∴能组成三角形,故B不符合题意;
C、∵3+4>5,∴能组成三角形,故C不符合题意;
D、∵3+5=8,∴不能组成三角形,故D符合题意.
故答案为:D.
【分析】根据三角形三边关系逐项进行判断,即可得出答案.
2.【答案】B
【知识点】三角形的面积;三角形的中线
【解析】【解答】解:是的中线,
,
,
、为的两个三等分点,
,,
,
故选:B.
【分析】由AD是△ABC的中线,则,由E、F为的两个三等分点,可得,,利用即可求解.
3.【答案】A
【知识点】三角形的稳定性
【解析】【解答】A.具有稳定性,符合题意;
B.不具有稳定性,故不符合题意;
C.不具有稳定性,故不符合题意;
D.不具有稳定性,故不符合题意,
故答案为:A
【分析】根据三角形具有稳定性,即可求出答案.
4.【答案】B
【知识点】三角形内角和定理
【解析】【解答】由三角形内角和定理得,∠C=180° ∠A ∠B=80°,
故答案为:B.
【分析】根据三角形内角和定理计算即可.
5.【答案】A
【知识点】三角形内角和定理
【解析】【解答】解:设∠A=3k°,∠B=4k°,∠C=5k°,
则3k°+4k°+5k°=180°,可得k=15°
∠A=45°,∠A=60°,∠A=75°
△ABC为锐角三角形.
所以A选项是正确的.
【分析】设∠A=3k°,由∠A,∠B,∠C的度数之比为3:4:5可得∠B=4k°,∠C=5k°,根据三角形的内角和定理列出关于k的方程,解方程求出∠A,∠B,∠C的度数 ,即可判断△ABC的形状.
6.【答案】A
【知识点】三角形的角平分线、中线和高;三角形的外角性质
【解析】【解答】解:∵∠BCA=40°,∠ABC=60°
∴∠BAC=80°,
∵AE平分∠BAC,
∴,
∵BF⊥AC,
∴∠BFA=90°,
∴∠ABF=10°,
∴∠BOE=∠BAO+∠ABO=40°+10°=50°,
∴=130°,
故答案为:.A
【分析】根据三角形内角和定理得出∠BAC=80°,根据三角形外角性质得出∠BOE=∠BAO+∠ABO,求出∠BAO,∠ABO即可,根据补角的定义求得.
7.【答案】C
【知识点】三角形的外角性质
【解析】【解答】解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°
∴∠ACD=2∠ACE=120°
∵∠ACD=∠B+∠A
∴∠A=∠ACD-∠B=120°-35°=85°
故答案为:C
【分析】根据角平分线性质可得 ∠ACE=60°,则∠ACD=120°,再根据三角形外角性质即可求出答案.
8.【答案】A
【知识点】多边形的对角线
【解析】【解答】一个正多边形的每一个内角是 ,
一个正多边形的每一个外角是180 -135 =45 ,
正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8 3=5,
故答案为:A.
【分析】根据正多边形的性质求出多边形的边数,再根据多边形对角线的规律求解即可。
9.【答案】C
【知识点】多边形的对角线
【解析】【解答】解:设这个多边形的边数为n,由题意得:,
解得:n=7.
故A,B,D错误,C正确.
故答案为:C.
【分析】设边数为n,表示出对角线条数后建立方程求解即可.
10.【答案】C
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故选:C.
【分析】根据四边形内角和为360°可得∠1+∠2+∠A+∠B=360°,再根据直角三角形的性质可得∠A+∠B=90°,进而可得∠1+∠2的和.
11.【答案】
【知识点】三角形三边关系
【解析】【解答】解:根据三角形的三边关系:,
解得:.
故答案为:.
【分析】根据三角形三边关系,列出不等式,解不等式即可求出答案.
12.【答案】3:2
【知识点】三角形的面积;三角形的角平分线
【解析】【解答】解:由作图痕迹可知,AD平分∠BAC,过点D分别作DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵
∴
∵AB=6,AC =4,
∴
故答案为:3:2.
【分析】由作图痕迹可知,AD平分∠BAC,过点D分别作DE⊥AB于点E,DF⊥AC于点F,根据角平分线的性质得到DE=DF,再根据三角形面积公式求解即可.
13.【答案】稳定
【知识点】三角形的稳定性
【解析】【解答】解:手机支架采用了三角形结构,这样设计依据的数学道理是三角形具有稳定性.
故答案为:稳定.
【分析】根据三角形具有稳定性进行解答即可.
14.【答案】300
【知识点】三角形内角和定理
【解析】【解答】解:∵在中有,∠C=30°,
∴∠3+∠4=180°-∠C=180°-30°=150°,
∵在中有,∠C=30°,
∴∠1+∠2=180°-∠C=180°-30°=150°,
将上面两式相加得:.
故答案为:300.
【分析】根据三角形内角和为180°可得∠3+∠4=150°,∠1+∠2=150°,然后将两式相加即可.
15.【答案】80°
【知识点】三角形的外角性质
【解析】【解答】解:∵∠ACD=∠A+∠B,∴∠A=∠ACD-∠B=120°-40°=80°.故答案为:80°.
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可求∠A.
16.【答案】10
【知识点】多边形的对角线
【解析】【解答】解:∵多边形从一个顶点出发可引出7条对角线,
∴,
解得.
故答案为:10.
【分析】根据从边形的一个顶点可以作对角线的条数为,求出边数即可求出答案.
17.【答案】360
【知识点】三角形的外角性质;多边形的外角和公式
【解析】【解答】解:如图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
【分析】利用三角形外角的性质可得∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,再利用多边形的外角和可得∠AHG+∠DNG+∠EGN=360°,从而可得∠A+∠B+∠C+∠D+∠E+∠F=360°.
18.【答案】
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵
∴
∴
故答案为:270°
【分析】根据三角形内角和定理可得,再根据四边形内角和定理即可求出答案.
19.【答案】(1)解:∵的三边长为4,10,x.
∴,
∴.
(2)解:∵的周长为偶数,是偶数,
∴x是偶数,
∵,
∴x的值可以是8或10或12.
【知识点】三角形三边关系
【解析】【分析】(1)利用三角形三边的关系可得,再求出x的取值范围即可;
(2)利用“的周长为偶数 ”和“”求出x的值即可.
(1)解:∵的三边长为4,10,x.
∴,
∴.
(2)解:∵的周长为偶数,是偶数,
∴x是偶数,
∵,
∴x的值可以是8或10或12.
20.【答案】解:∵,CD是AB边上的高,
∴,代入已知条件得
解得
【知识点】三角形的面积
【解析】【分析】根据三角形面积进行求解,即根据直角三角形面积:两直角边乘积的一半等于斜边与斜边上的高的乘积的一半,计算求解即可.
21.【答案】解:如图所示:
根据三角形具有稳定性.
【知识点】三角形的稳定性
【解析】【分析】根据三角形具有稳定性进行画图即可.
22.【答案】(1)130;50
(2)解:如图①,、的平分线相交于,
,,
,
,,
,,
;
如图②,、外角的平分线相交于,
,,
,
,,,
,,
,
即
【知识点】角的运算;三角形内角和定理;三角形的角平分线
【解析】【解答】解:(1)如图①,∵∠ABC、∠ACB的平分线相交于M,
∴∠MBC=∠ABC,∠MCB=∠ACB,
∴∠MBC+∠MCB=(∠ABC+∠ACB),
∵∠MBC+∠MCB+∠BMC=180°,∠ABC+∠ACB+∠A=180°,
∴∠MBC+∠MCB=180° ∠BMC,∠ABC+∠ACB=180° ∠A,
∴∠BMC=90°+∠A,
∵∠A=80°,
∴∠BMC=130°;
如图②,∵∠ABC、∠ACB外角的平分线相交于N,
∴∠NBC=∠PBC,∠NCB=∠QCB,
∴∠NBC+∠NCB=(∠PBC+∠QCB),
∵∠NBC+∠NCB+∠BNC=180°,∠PBC=∠A+∠ACB,∠QCB=∠A+∠ABC,
∴∠NBC+∠NCB=180° ∠BNC,∠PBC+∠QBC=∠A+∠ABC+∠ACB+∠A=180°+∠A,
∴180° ∠BNC=(180°+∠A),
即∠BNC=90° ∠A,
∵∠A=80°,
∴∠BNC=50°;
故答案为:130°;50°.
【分析】(1)由角平分线的定义可得∠MBC+∠MCB=(∠ABC+∠ACB),再利用三角形的内角和定理可得∠M=90°+∠A,进而可求解;由角平分线的定义可得∠NBC+∠NCB=(∠PBC+∠QCB),再利用三角形的内角和定理可得∠N=90° ∠A,进而可求解;
(2)由角平分线的定义可得∠MBC+∠MCB=(∠ABC+∠ACB),再利用三角形的内角和定理可得∠M=90°+∠A,进而可求解;由角平分线的定义可得∠NBC+∠NCB=(∠PBC+∠QCB),再利用三角形的内角和定理可得∠N=90° ∠A,进而可求解.
23.【答案】解:依题意有,
则
【知识点】多边形的对角线
【解析】【分析】根据多边形性质可求出m,n,t值,再代入代数式即可求出答案.
24.【答案】(1)解:设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是;
(2)解:因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,
当截线经过多边形的个顶点时,多边形的边数减少了条边,
内角和;
当截线经过多边形一个顶点时,多边形的边数不变,
内角和;
当截线不经过正多形的顶点时,多边形的边数增加一条边,
内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
【知识点】多边形内角与外角
【解析】【分析】(1)设多边形的一个外角为,则与其相邻的内角等于,根据题意列出方程,求得,进而根据多边形的外角和为,即可求解;
(2)因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,分3种情况讨论,即可求解.
25.【答案】(1)=
(2)解:,
的周长的周长,
即①,
又②,
①②得.,
解得,
②①得,,
解得,
和的长分别为:,.
【知识点】解二元一次方程;三角形的角平分线、中线和高;三角形的面积
【解析】【分析】(1)根据三角形的中线平分三角形的面积可得答案;
(2)由BD=CD可知△ABD和△ADC之差就是AB与AC的差,结合已知AB+AC=14可得关于AB、AC的二元一次方程组,利用加减消元法求解即可.
26.【答案】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠PNB=∠P+∠PAB,∠PNB=∠B+∠PCB,∠PMD=∠P+∠PCD,∠PMD=∠D+∠DAP,
∴∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2).
【知识点】三角形的外角性质;角平分线的概念
【解析】【解答】解:(2) ∠P=,理由如下:
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
【分析】(1)根据角平分线可以得到∠DAP=∠PAB,∠DCP=∠PCB,利用三角形的任意一个外角等于与之不相邻的两个内角的和得∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP,然后根据等式性质得出得出2∠P=∠B+∠D,结合题目给出的已知条件即可求解;
(2) 利用三角形的任意一个外角等于与之不相邻的两个内角的和得∠PCD-∠DAP=∠D-∠P,∠DAB-∠DCB=∠B-∠DB,结合题目中的已知条件得∠DAB-∠DCB=3(∠DAP-∠DCP),从而整体代入得出∠P和∠D、∠B之间存在的数量关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2024-2025学年八年级数学上册《第十一章 三角形》单元测试题 人教版
一、选择题(共10题;共30分)
1.(3分)下列长度(单位cm)的线段不能组成三角形的是( )
A.3,3,3 B.3,5,5 C.3,4,5 D.3,5,8
2.(3分)如图,的面积为18,为的中线,E、F为的两个三等分点,连接,则图中阴影部分的面积和为( )
A.4 B.6 C.8 D.9
3.(3分)下列图形具有稳定性的是( )
A. B.
C. D.
4.(3分)在△ABC中,∠A=60°,∠B=40°,则∠C等于( ).
A.100° B.80° C.60° D.40°
5.(3分)在△ABC中,∠A,∠B,∠C的度数之比为3:4:5,那么△ABC是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
6.(3分)如图,在△ABC中,∠BCA=40°,∠ABC=60°.若BF是△ABC的高,与角平分线AE相交于点O,则∠EOF的度数为( )
A.130° B.70° C.110 D.100°
7.(3分)如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
A.35° B.95° C.85° D.75°
8.(3分)一个正多边形的每一个内角是 ,则从这个正多边形的一个顶点出发可作( )条对角线.
A.5 B.4 C.3 D.2
9.(3分)若一个多边形的对角线条数恰好为边数的2倍,则这个多边形的边数为( )
A.9 B.8 C.7 D.6
10.(3分)如图,已知△ABC为直角三角形,∠C=90°,若沿图中虚线剪去∠C,则∠1+∠2等于( )
A.90° B.135° C.270° D.315°
二、填空题(共8题;共24分)
11.(3分)一个三角形的两边长为5和7,则第三边a的取值范围是 .
12.(3分)如图,AD是△ABC的角平分线,AB=6,AC=4,则△ABD与△ACD的面积之比为 .
13.(3分)如图,手机支架采用了三角形结构,这样设计依据的数学道理是三角形具有 性.
14.(3分)如图, °.
15.(3分)如图,在△ABC中,点D是BC延长线上一点,∠B=40°,∠ACD=120°,则∠A的余角是 .
16.(3分)过多边形的一个顶点能引出7条对角线,则这个多边形的边数是 .
17.(3分)如图,∠A+∠B+∠C+∠D+∠E+∠F的和等于 度.
18.(3分)如图,在一个三角形的纸片()中,,则图中的度数为 .
三、解答题(共8题;共66分)
19.(6分)已知,的三边长为4,10,x.
(1)(3分)求x的取值范围.
(2)(3分)当的周长为偶数时,求x.
20.(6分)如图,中,,,,,CD是AB边上的高.求CD的长.
21.(8分)小辉用7根木条钉成一个七边形的木架,他为了使该木架稳固,想在其中加上四根木条,请你在图1、2、3中画出你的三种想法,并说明加上木条后使该木架稳固所用的数学道理
22.(8分)已知:中,图中、的平分线相交于,图中、的外角平分线相交于.
(1)(4分)若, ,
(2)(4分)若,试用表示和.
23.(8分)已知:从边形的一个顶点出发共有条对角线;从边形的一个顶点出发的所有对角线把边形分成个三角形;正边形的边长为,周长为.求的值.
24.(10分) 在一个各内角都相等的多边形中,每一个内角都比相邻外角的倍还大,
(1)(5分)求这个多边形的边数;
(2)(5分)若将这个多边形剪去一个角,剩下多边形的内角和是多少?
25.(10分)如图,在中,为边上的中线.
(1)(4分) (填“>”、“<”或“=”);
(2)(6分)若的周长比的周长多4,且,求的长.
26.(10分)如图1,AB与CD相交于点O,若,,和的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试求:
(1)的度数;
(2)设,,,,其他条件不变,如图2,试问与、之间存在着怎样的数量关系(用、表示),直接写出结论.
答案解析部分
1.【答案】D
【知识点】三角形三边关系
【解析】【解答】解:A、∵3+3>3,∴能组成三角形,故A不符合题意;
B、∵3+5>5,∴能组成三角形,故B不符合题意;
C、∵3+4>5,∴能组成三角形,故C不符合题意;
D、∵3+5=8,∴不能组成三角形,故D符合题意.
故答案为:D.
【分析】根据三角形三边关系逐项进行判断,即可得出答案.
2.【答案】B
【知识点】三角形的面积;三角形的中线
【解析】【解答】解:是的中线,
,
,
、为的两个三等分点,
,,
,
故选:B.
【分析】由AD是△ABC的中线,则,由E、F为的两个三等分点,可得,,利用即可求解.
3.【答案】A
【知识点】三角形的稳定性
【解析】【解答】A.具有稳定性,符合题意;
B.不具有稳定性,故不符合题意;
C.不具有稳定性,故不符合题意;
D.不具有稳定性,故不符合题意,
故答案为:A
【分析】根据三角形具有稳定性,即可求出答案.
4.【答案】B
【知识点】三角形内角和定理
【解析】【解答】由三角形内角和定理得,∠C=180° ∠A ∠B=80°,
故答案为:B.
【分析】根据三角形内角和定理计算即可.
5.【答案】A
【知识点】三角形内角和定理
【解析】【解答】解:设∠A=3k°,∠B=4k°,∠C=5k°,
则3k°+4k°+5k°=180°,可得k=15°
∠A=45°,∠A=60°,∠A=75°
△ABC为锐角三角形.
所以A选项是正确的.
【分析】设∠A=3k°,由∠A,∠B,∠C的度数之比为3:4:5可得∠B=4k°,∠C=5k°,根据三角形的内角和定理列出关于k的方程,解方程求出∠A,∠B,∠C的度数 ,即可判断△ABC的形状.
6.【答案】A
【知识点】三角形的角平分线、中线和高;三角形的外角性质
【解析】【解答】解:∵∠BCA=40°,∠ABC=60°
∴∠BAC=80°,
∵AE平分∠BAC,
∴,
∵BF⊥AC,
∴∠BFA=90°,
∴∠ABF=10°,
∴∠BOE=∠BAO+∠ABO=40°+10°=50°,
∴=130°,
故答案为:.A
【分析】根据三角形内角和定理得出∠BAC=80°,根据三角形外角性质得出∠BOE=∠BAO+∠ABO,求出∠BAO,∠ABO即可,根据补角的定义求得.
7.【答案】C
【知识点】三角形的外角性质
【解析】【解答】解:∵CE是△ABC的外角∠ACD的平分线,∠ACE=60°
∴∠ACD=2∠ACE=120°
∵∠ACD=∠B+∠A
∴∠A=∠ACD-∠B=120°-35°=85°
故答案为:C
【分析】根据角平分线性质可得 ∠ACE=60°,则∠ACD=120°,再根据三角形外角性质即可求出答案.
8.【答案】A
【知识点】多边形的对角线
【解析】【解答】一个正多边形的每一个内角是 ,
一个正多边形的每一个外角是180 -135 =45 ,
正多边形的边数:360÷45=8,
从这个正多边形的一个顶点出发,共可以作对角线的条数为:8 3=5,
故答案为:A.
【分析】根据正多边形的性质求出多边形的边数,再根据多边形对角线的规律求解即可。
9.【答案】C
【知识点】多边形的对角线
【解析】【解答】解:设这个多边形的边数为n,由题意得:,
解得:n=7.
故A,B,D错误,C正确.
故答案为:C.
【分析】设边数为n,表示出对角线条数后建立方程求解即可.
10.【答案】C
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵四边形的内角和为360°,直角三角形中两个锐角和为90°
∴∠1+∠2=360°﹣(∠A+∠B)=360°﹣90°=270°.
故选:C.
【分析】根据四边形内角和为360°可得∠1+∠2+∠A+∠B=360°,再根据直角三角形的性质可得∠A+∠B=90°,进而可得∠1+∠2的和.
11.【答案】
【知识点】三角形三边关系
【解析】【解答】解:根据三角形的三边关系:,
解得:.
故答案为:.
【分析】根据三角形三边关系,列出不等式,解不等式即可求出答案.
12.【答案】3:2
【知识点】三角形的面积;三角形的角平分线
【解析】【解答】解:由作图痕迹可知,AD平分∠BAC,过点D分别作DE⊥AB于点E,DF⊥AC于点F,
∴DE=DF,
∵
∴
∵AB=6,AC =4,
∴
故答案为:3:2.
【分析】由作图痕迹可知,AD平分∠BAC,过点D分别作DE⊥AB于点E,DF⊥AC于点F,根据角平分线的性质得到DE=DF,再根据三角形面积公式求解即可.
13.【答案】稳定
【知识点】三角形的稳定性
【解析】【解答】解:手机支架采用了三角形结构,这样设计依据的数学道理是三角形具有稳定性.
故答案为:稳定.
【分析】根据三角形具有稳定性进行解答即可.
14.【答案】300
【知识点】三角形内角和定理
【解析】【解答】解:∵在中有,∠C=30°,
∴∠3+∠4=180°-∠C=180°-30°=150°,
∵在中有,∠C=30°,
∴∠1+∠2=180°-∠C=180°-30°=150°,
将上面两式相加得:.
故答案为:300.
【分析】根据三角形内角和为180°可得∠3+∠4=150°,∠1+∠2=150°,然后将两式相加即可.
15.【答案】80°
【知识点】三角形的外角性质
【解析】【解答】解:∵∠ACD=∠A+∠B,∴∠A=∠ACD-∠B=120°-40°=80°.故答案为:80°.
【分析】根据三角形的一个外角等于与它不相邻的两个内角的和可求∠A.
16.【答案】10
【知识点】多边形的对角线
【解析】【解答】解:∵多边形从一个顶点出发可引出7条对角线,
∴,
解得.
故答案为:10.
【分析】根据从边形的一个顶点可以作对角线的条数为,求出边数即可求出答案.
17.【答案】360
【知识点】三角形的外角性质;多边形的外角和公式
【解析】【解答】解:如图所示,
∵∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,
∴∠AHG+∠DNG+∠EGN=∠A+∠B+∠C+∠D+∠E+∠F,
又∵∠AHG、∠DNG、∠EGN是△GHN的三个不同的外角,
∴∠AHG+∠DNG+∠EGN=360°,
∴∠A+∠B+∠C+∠D+∠E+∠F=360°.
故答案为:360.
【分析】利用三角形外角的性质可得∠AHG=∠A+∠B,∠DNG=∠C+∠D,∠EGN=∠E+∠F,再利用多边形的外角和可得∠AHG+∠DNG+∠EGN=360°,从而可得∠A+∠B+∠C+∠D+∠E+∠F=360°.
18.【答案】
【知识点】三角形内角和定理;多边形内角与外角
【解析】【解答】解:∵
∴
∴
故答案为:270°
【分析】根据三角形内角和定理可得,再根据四边形内角和定理即可求出答案.
19.【答案】(1)解:∵的三边长为4,10,x.
∴,
∴.
(2)解:∵的周长为偶数,是偶数,
∴x是偶数,
∵,
∴x的值可以是8或10或12.
【知识点】三角形三边关系
【解析】【分析】(1)利用三角形三边的关系可得,再求出x的取值范围即可;
(2)利用“的周长为偶数 ”和“”求出x的值即可.
(1)解:∵的三边长为4,10,x.
∴,
∴.
(2)解:∵的周长为偶数,是偶数,
∴x是偶数,
∵,
∴x的值可以是8或10或12.
20.【答案】解:∵,CD是AB边上的高,
∴,代入已知条件得
解得
【知识点】三角形的面积
【解析】【分析】根据三角形面积进行求解,即根据直角三角形面积:两直角边乘积的一半等于斜边与斜边上的高的乘积的一半,计算求解即可.
21.【答案】解:如图所示:
根据三角形具有稳定性.
【知识点】三角形的稳定性
【解析】【分析】根据三角形具有稳定性进行画图即可.
22.【答案】(1)130;50
(2)解:如图①,、的平分线相交于,
,,
,
,,
,,
;
如图②,、外角的平分线相交于,
,,
,
,,,
,,
,
即
【知识点】角的运算;三角形内角和定理;三角形的角平分线
【解析】【解答】解:(1)如图①,∵∠ABC、∠ACB的平分线相交于M,
∴∠MBC=∠ABC,∠MCB=∠ACB,
∴∠MBC+∠MCB=(∠ABC+∠ACB),
∵∠MBC+∠MCB+∠BMC=180°,∠ABC+∠ACB+∠A=180°,
∴∠MBC+∠MCB=180° ∠BMC,∠ABC+∠ACB=180° ∠A,
∴∠BMC=90°+∠A,
∵∠A=80°,
∴∠BMC=130°;
如图②,∵∠ABC、∠ACB外角的平分线相交于N,
∴∠NBC=∠PBC,∠NCB=∠QCB,
∴∠NBC+∠NCB=(∠PBC+∠QCB),
∵∠NBC+∠NCB+∠BNC=180°,∠PBC=∠A+∠ACB,∠QCB=∠A+∠ABC,
∴∠NBC+∠NCB=180° ∠BNC,∠PBC+∠QBC=∠A+∠ABC+∠ACB+∠A=180°+∠A,
∴180° ∠BNC=(180°+∠A),
即∠BNC=90° ∠A,
∵∠A=80°,
∴∠BNC=50°;
故答案为:130°;50°.
【分析】(1)由角平分线的定义可得∠MBC+∠MCB=(∠ABC+∠ACB),再利用三角形的内角和定理可得∠M=90°+∠A,进而可求解;由角平分线的定义可得∠NBC+∠NCB=(∠PBC+∠QCB),再利用三角形的内角和定理可得∠N=90° ∠A,进而可求解;
(2)由角平分线的定义可得∠MBC+∠MCB=(∠ABC+∠ACB),再利用三角形的内角和定理可得∠M=90°+∠A,进而可求解;由角平分线的定义可得∠NBC+∠NCB=(∠PBC+∠QCB),再利用三角形的内角和定理可得∠N=90° ∠A,进而可求解.
23.【答案】解:依题意有,
则
【知识点】多边形的对角线
【解析】【分析】根据多边形性质可求出m,n,t值,再代入代数式即可求出答案.
24.【答案】(1)解:设多边形的一个外角为,则与其相邻的内角等于,
由题意,得,解得.
即多边形的每个外角为.
又多边形的外角和为,
多边形的外角个数.
多边形的边数,
答:这个多边形的边数是;
(2)解:因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,
当截线经过多边形的个顶点时,多边形的边数减少了条边,
内角和;
当截线经过多边形一个顶点时,多边形的边数不变,
内角和;
当截线不经过正多形的顶点时,多边形的边数增加一条边,
内角和.
答:将这个多边形剪去一个角,剩下多边形的内角和是或或.
【知识点】多边形内角与外角
【解析】【分析】(1)设多边形的一个外角为,则与其相邻的内角等于,根据题意列出方程,求得,进而根据多边形的外角和为,即可求解;
(2)因为剪掉一个角以后,多边形的边数可能增加了条,也可能减少了条,或者不变,分3种情况讨论,即可求解.
25.【答案】(1)=
(2)解:,
的周长的周长,
即①,
又②,
①②得.,
解得,
②①得,,
解得,
和的长分别为:,.
【知识点】解二元一次方程;三角形的角平分线、中线和高;三角形的面积
【解析】【分析】(1)根据三角形的中线平分三角形的面积可得答案;
(2)由BD=CD可知△ABD和△ADC之差就是AB与AC的差,结合已知AB+AC=14可得关于AB、AC的二元一次方程组,利用加减消元法求解即可.
26.【答案】解:(1)∵AP是∠DAB的角平分线,CP是∠DCB的角平分线,
∴∠DAP=∠PAB,∠DCP=∠PCB,
∵∠PNB=∠P+∠PAB,∠PNB=∠B+∠PCB,∠PMD=∠P+∠PCD,∠PMD=∠D+∠DAP,
∴∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP
∴∠P+∠PAB+∠P+∠PCD=∠B+∠PCB+∠D+∠DAP
∴2∠P=∠B+∠D
∵∠B=28°,∠D=38°
∴∠P=33°
(2).
【知识点】三角形的外角性质;角平分线的概念
【解析】【解答】解:(2) ∠P=,理由如下:
∵∠P+∠PCD=∠D+∠DAP
∴∠PCD-∠DAP=∠D-∠P
∵∠D+∠DAO=∠B+∠OCB
∴∠DAB-∠DCB=∠B-∠D
∵,
∴∠DAB-∠DCB=3(∠DAP-∠DCP)
∴∠B-∠D=3(∠P-∠D)
∵,
∴∠P=
【分析】(1)根据角平分线可以得到∠DAP=∠PAB,∠DCP=∠PCB,利用三角形的任意一个外角等于与之不相邻的两个内角的和得∠P+∠PAB=∠B+∠PCB,∠P+∠PCD=∠D+∠DAP,然后根据等式性质得出得出2∠P=∠B+∠D,结合题目给出的已知条件即可求解;
(2) 利用三角形的任意一个外角等于与之不相邻的两个内角的和得∠PCD-∠DAP=∠D-∠P,∠DAB-∠DCB=∠B-∠DB,结合题目中的已知条件得∠DAB-∠DCB=3(∠DAP-∠DCP),从而整体代入得出∠P和∠D、∠B之间存在的数量关系.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
