浙教版七上期中复习—中档题(含解析)
文档属性
| 名称 | 浙教版七上期中复习—中档题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 196.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 22:13:28 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
浙教版七上期中复习—中档题
一.选择题(共6小题)
1.下列说法中正确的是( )
A.有理数与数轴上的点一一对应
B.负数有立方根
C.如果三个有理数的积为正数,那么这三个数中负因数的个数为0
D.若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a≤7.304
2.下列说法中:①立方根等于本身的是﹣1、0、1; ②平方根等于本身的数是0、1;③两个无理数的和一定是无理数; ④实数与数轴上的点是一一对应的;⑤是负分数;其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
3.一个是三位数a放在一个两位数b前面组成一个五位数,则这个五位数可以用代数式表示为( )
A.ab B.1000a+100b
C.100a+1000b D.100a+b
4.下列说法:(1)的系数是;(2)x2+2xy﹣3的常数项是3;(3)﹣2yx2与2x2y是同类项;(4)是三次二项式.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
5.若a2﹣3b=4,则﹣6b+2a2+2012值为( )
A.2008 B.2016 C.2020 D.2004
6.为了求1+7+72+...+72023的值,可令S=1+7+72+...+72023,则7S=7+72+...+72023+72024,因此7S﹣S=72024﹣1,所以.这种方法称为“错位相减法”.请参考以上推理计算:1×21+2×22+3×23+ +9×29=( )
A.213 B.213+2 C.213+4 D.213+8
二.填空题(共2小题)
7.近似数4.50万精确到 位.
8.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.则b= ,若前n个格子中所填整数之和是2023,则n的值是 .
7 a b c ﹣4 1 …
三.解答题(共7小题)
9.计算:
(1);
(2).
10.(1)已知单项式2x2my7与单项式5x6yn﹣8是同类项,求m2﹣3n的值.
(2)已知关于x的多项式mx3﹣3x2+4x+x3+x2﹣nx不含三次项和一次项,求(m﹣n)2的值.
11.已知.
(1)求a0的值;
(2)求a1+a2+a3+a4+a5的值;
(3)求a1+a3+a5的值.
12.数轴是初中数学的一个重要的工具,研究数轴可以发现许多重要的规律.如数轴上的点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
解决问题:现数轴上有一点A表示的数为﹣10,点B表示的数为18,点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒(t>0).
(1)填空:
①A、B两点之间的距离AB= ,线段AB的中点表示的数为 .
②当t= 时,P、Q两点相遇,相遇点所表示的数为 .
(2)求当t为何值时,PQAB.
(3)折叠数轴使点A、P重合,折点记为M,还原后再折叠数轴使点B、P重合,折点记为N,点P在运动过程中,M、N两点间的距离是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长度.
13.如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为8,点P从点A出发以每秒2个单位长度的速度在数轴上向右运动,当点P到达点B后立即返回,再以每秒3个单位长度的速度向左运动.设点P运动时间为t(s).
(1)当t=7时,点P表示的有理数为 ;
(2)当点P运动到AB中点时,t的值为 ;
(3)当点P与原点距离是2个单位长度时,求t的值.
14.阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
又如,表示0的点D到点A的距离是1,到点B的距离是2.那么点D就不是【A,B】的好点,但点D是【B,A】的好点:
知识运用:
(1)如图1,点B是【D,C】的好点吗? (填是或不是);
(2)如图2,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止,当t为何值时,P、A和B中恰有一个点为其余两点的好点?
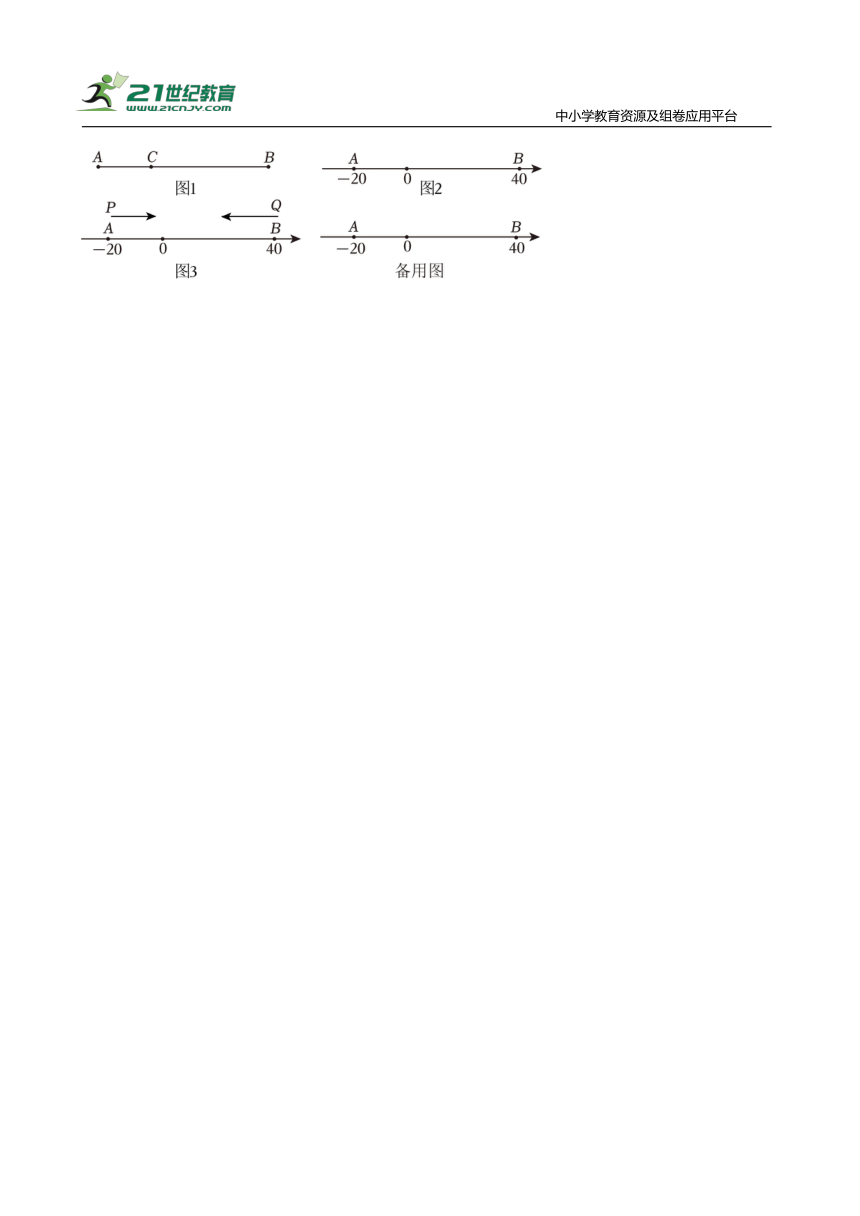
15.【新知理解】如图①,点C在线段AB上,图中的三条线段AB、AC和BC.若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“蓝青点”.
(1)填空:线段的中点 这条线段的“蓝青点”;(填“是”或“不是”)
【问题解决】
(2)如图②,点A和B在数轴上表示的数分别是﹣20和40,点C是线段AB的“蓝青点”,求点C在数轴上表示的数.
【应用拓展】
(3)在(2)的条件下,动点P从点A出发,以每秒2个单位长度的速度沿AB向点B匀速运动;动点Q从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.点P、Q同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为t秒,当t为何值时,A、P、Q三点中,其中一点恰好是另外两点为端点的线段的“蓝青点”?(直接写出答案).
浙教版七上期中复习—中档题
一.选择题(共6小题)
1.下列说法中正确的是( )
A.有理数与数轴上的点一一对应
B.负数有立方根
C.如果三个有理数的积为正数,那么这三个数中负因数的个数为0
D.若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a≤7.304
【思路点拔】利用实数与数轴的关系,立方根的定义,有理数的乘法,近似数的精确度对各选项分析判断后利用排除法求解.
【解答】解:∵数轴上的点有的表示有理数,有的表示无理数,而有理数和无理数统称为实数,
∴实数与数轴上的点一一对应,
故A错误,不符合题意;
负数有立方根,故B正确,符合题意;
如果三个有理数的积为正数,那么这三个数中负因数的个数为0或三个,
故C错误,不符合题意;
若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a<7.305.
故D错误,不符合题意.
故选:B.
2.下列说法中:①立方根等于本身的是﹣1、0、1; ②平方根等于本身的数是0、1;③两个无理数的和一定是无理数; ④实数与数轴上的点是一一对应的;⑤是负分数;其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
【思路点拔】根据立方根、平方根、无理数以及实数和数轴的概念逐一判断,即可得到答案.
【解答】解:①立方根等于本身的是﹣1、0、1,原说法正确;
②平方根等于本身的数是0,原说法错误;
③(﹣π)+π=0,即两个无理数的和不一定是无理数,原说法错误;
④实数与数轴上的点是一一对应的,原说法正确;
⑤是无理数,原说法错误;
∴正确的说法有①④,共2个,
故选:C.
3.一个是三位数a放在一个两位数b前面组成一个五位数,则这个五位数可以用代数式表示为( )
A.ab B.1000a+100b
C.100a+1000b D.100a+b
【思路点拔】a原来的最高位是千位,现在的最高位是十万位,扩大了100倍,b不变.
【解答】解:三位数a放在一个两位数b前面相当于a扩大了100倍,那么这个五位数为(100a+b).故选D.
4.下列说法:(1)的系数是;(2)x2+2xy﹣3的常数项是3;(3)﹣2yx2与2x2y是同类项;(4)是三次二项式.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【思路点拔】根据同类项的定义、单项式的系数的定义、多项式的项和次数的定义逐项判断即可.
【解答】解:(1)的系数是,正确;
(2)x2+2xy﹣3的常数项是﹣3,原说法错误;
(3)﹣2yx2与2x2y是同类项,正确;
(4)是三次二项式,正确;
所以正确的有3个,
故选:C.
5.若a2﹣3b=4,则﹣6b+2a2+2012值为( )
A.2008 B.2016 C.2020 D.2004
【思路点拔】将a2﹣3b=4代入原式=2(a2﹣3b)+2012,计算可得.
【解答】解:当a2﹣3b=4时,
原式=2(a2﹣3b)+2012
=2×4+2012
=2020,
故选:C.
6.为了求1+7+72+...+72023的值,可令S=1+7+72+...+72023,则7S=7+72+...+72023+72024,因此7S﹣S=72024﹣1,所以.这种方法称为“错位相减法”.请参考以上推理计算:1×21+2×22+3×23+ +9×29=( )
A.213 B.213+2 C.213+4 D.213+8
【思路点拔】设S=1×21+2×22+3×23+ +9×29,则2S=1×22+2×23+3×24+ +9×29+9×210,两式相减得2S=1×22+2×23+3×24+ +9×29+9×210,再设P=21+22+23+ +9×29,则2P=22+23+24+ +9×29+210,再将两式相减得P=210﹣2,由此即可得出答案.
【解答】解:设S=1×21+2×22+3×23+ +9×29,
∴2S=1×22+2×23+3×24+ +9×29+9×210,
∴2S﹣S=9×210﹣(21+22+23+ +29),
即S=9×210﹣(21+22+23+ +29),
设P=21+22+23+ +29,
∴2P=22+23+24+ +29+210,
∴2P﹣P=210﹣2,
即P=210﹣2,
∴S=9×210﹣210+2=8×210+2=23×210+2=213+2,
∴1×21+2×22+3×23+ +9×29=213+2.
故选:B.
二.填空题(共2小题)
7.近似数4.50万精确到 百 位.
【思路点拔】根据近似数4.50万的最后的尾数0,在百位上,可知近似数4.50万精确到百位.
【解答】解:近似数4.50万精确到百位,
故答案为:百.
8.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.则b= 1 ,若前n个格子中所填整数之和是2023,则n的值是 1517 .
7 a b c ﹣4 1 …
【思路点拔】根据题意得,7+a+b=a+b+c,a+b+c=b+c﹣4,b+c﹣4=c﹣4+1,得c=7,a=﹣4,b=1,得这组数为7,﹣4,1,7,﹣4,1,......,得三个相邻格子中的数之和为7﹣4+1=4,2023÷4=505余3,即可得n=505×3+2=1517.
【解答】解:根据题意得,7+a+b=a+b+c,a+b+c=b+c﹣4,b+c﹣4=c﹣4+1,
∴c=7,a=﹣4,b=1,
∴这组数为7,﹣4,1,7,﹣4,1,......,
∴三个相邻格子中的数之和为7﹣4+1=4,2023÷4=505余3,
∴n=505×3+2=1517.
故答案为:1;1517.
三.解答题(共7小题)
9.计算:
(1);
(2).
【思路点拔】(1)利用乘法分配律计算即可得到结果;
(2)先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
【解答】解:(1)
=﹣8+21﹣10
=3;
(2)
.
10.(1)已知单项式2x2my7与单项式5x6yn﹣8是同类项,求m2﹣3n的值.
(2)已知关于x的多项式mx3﹣3x2+4x+x3+x2﹣nx不含三次项和一次项,求(m﹣n)2的值.
【思路点拔】(1)根据同类项的定义可得:2m=6,n﹣8=7,从而可得:m=3,n=15,然后代入式子中进行计算即可解答;
(2)先利用合并同类项的法则进行计算,再根据题意可得:m+1=0,4﹣n=0,从而可得m=﹣1,n=4,然后代入式子中进行计算即可解答.
【解答】解:(1)∵单项式2x2my7与单项式5x6yn﹣8是同类项,
∴2m=6,n﹣8=7,
解得:m=3,n=15,
∴m2﹣3n=32﹣3×15=9﹣45=﹣36;
(2)mx3﹣3x2+4x+x3+x2﹣nx=(m+1)x3﹣2x2+(4﹣n)x,
由题意得:m+1=0,4﹣n=0,
解得:m=﹣1,n=4,
∴(m﹣n)2=(﹣1﹣4)2=25.
11.已知.
(1)求a0的值;
(2)求a1+a2+a3+a4+a5的值;
(3)求a1+a3+a5的值.
【思路点拔】(1)把x=0代入代数式计算即可;
(2)把x=1代入代数式结合(1)中的结果即可求出a1+a2+a3+a4+a5的值;
(3)把x=﹣1代入代数式结合(1)(2)中的结果即可求出a1+a3+a5的值.
【解答】解:(1)令x=0,则;
(2)令x=1,则25=32,
所以a1+a2+a3+a4+a5=32﹣(﹣1)=32+1=33;
(3)令x=﹣1,则,
所以﹣a5+a4﹣a3+a2﹣a1=﹣1024﹣(﹣1)=﹣1023①,
由(2)知a1+a2+a3+a4+a5=33②,
②﹣①,得2a1+2a3+2a5=1056,
所以a1+a3+a5=528.
12.数轴是初中数学的一个重要的工具,研究数轴可以发现许多重要的规律.如数轴上的点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
解决问题:现数轴上有一点A表示的数为﹣10,点B表示的数为18,点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒(t>0).
(1)填空:
①A、B两点之间的距离AB= 28 ,线段AB的中点表示的数为 4 .
②当t= 时,P、Q两点相遇,相遇点所表示的数为 .
(2)求当t为何值时,PQAB.
(3)折叠数轴使点A、P重合,折点记为M,还原后再折叠数轴使点B、P重合,折点记为N,点P在运动过程中,M、N两点间的距离是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长度.
【思路点拔】(1)①根据已知可得AB=|﹣10﹣18|=28,中点表示的数为4;
②运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,可得﹣10+2t=18﹣t,解得t,故当t时,P、Q两点相遇,相遇点所表示的数为;
(2)运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,可得|﹣10+2t﹣(18﹣t)|28,解得t=14或t;
(3)根据题意,点M是AP的中点,N是BP的中点,得点M表示的数为﹣10+t,点N表示的数为4+t,从而MN=|﹣10+t﹣(4+t)|=14.
【解答】解:(1)①由题意可得,
A、B两点之间的距离AB=|﹣10﹣18|=28,线段AB的中点表示的数为4,
故答案为:28,4;
②运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,
∴﹣10+2t=18﹣t,
解得t,
此时﹣10+2t=﹣10+2,
∴当t时,P、Q两点相遇,相遇点所表示的数为,
故答案为:,;
(2)运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,
∴|﹣10+2t﹣(18﹣t)|28,
解得t=14或t;
∴当t=14或t时,PQAB;
(3)点P在运动过程中,线段MN的长度不发生变化,理由如下:
根据题意,点M是AP的中点,N是BP的中点,
∴点M表示的数为:10+t,点N表示的数为:4+t,
∴MN=|﹣10+t﹣(4+t)|=14,
∴点P在运动过程中,线段MN的长度不发生变化.
13.如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为8,点P从点A出发以每秒2个单位长度的速度在数轴上向右运动,当点P到达点B后立即返回,再以每秒3个单位长度的速度向左运动.设点P运动时间为t(s).
(1)当t=7时,点P表示的有理数为 5 ;
(2)当点P运动到AB中点时,t的值为 3或8 ;
(3)当点P与原点距离是2个单位长度时,求t的值.
【思路点拔】(1)当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),列方程求解.
(2)用含t代数式表示点P所表示的数,使其等于8,进而求解.
(3)点P到原点距离为2的数为2或﹣2,分类讨论点P从A向B和从B向A运动时点P表示的数为±2,进而求解.
(4)根据BP=3AP求出点P所表示的数,然后列方程求解.
【解答】解:(1)点P从A向B运动到B用时(4+8)÷2=6(s),
当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),
当t=7时,8﹣3(t﹣6)=8﹣3=5,
故答案为:5;
(2)当点P运动到AB中点时,点P表示的数为:2,
当点P从A向B运动到AB中点时,
由题意得﹣4+2t=2,
解得t=3.
当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),
由题意得8﹣3(t﹣6)=2,
解得t=8.
故答案为:3或8;
(3)当点P表示的数为2或﹣2时满足题意,
解﹣4+2t=﹣2得t=1,
解﹣4+2t=2得t=3,
解8﹣3(t﹣6)=2得t=8,
解8﹣3(t﹣6)=﹣2得t.
故答案为:1或3或8或.
14.阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
又如,表示0的点D到点A的距离是1,到点B的距离是2.那么点D就不是【A,B】的好点,但点D是【B,A】的好点:
知识运用:
(1)如图1,点B是【D,C】的好点吗? 是 (填是或不是);
(2)如图2,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止,当t为何值时,P、A和B中恰有一个点为其余两点的好点?
【思路点拔】(1)根据定义计算BD、BC,验证是否具有BD=2BC即可;
(2)设点P表示的数为x,分情况讨论:①P为【A,B】的好点;②A为【B,P】的好点;③P为【B,A】的好点;④A为【P,B】的好点;⑤B为【A,P】的好点.
【解答】解:(1)∵BD=2,BC=1,BD=2BC
∴点B是【D,C】的好点.
故答案为:是;
(2)设点P表示的数为x,分以下几种情况:
①P为【A,B】的好点
由题意,得x﹣(﹣40)=2(20﹣x),
解得x=0,
t=20÷2=10(秒);
②A为【B,P】的好点
由题意,得20﹣(﹣40)=2[x﹣(﹣40)],
解得x=﹣10,
t=[20﹣(﹣10)]÷2=15(秒);
③P为【B,A】的好点
由题意,得20﹣x=2[x﹣(﹣40)],
解得x=﹣20,
t=[20﹣(﹣20)]÷2=20(秒);
④A为【P,B】的好点
由题意得x﹣(﹣40)=2[20﹣(﹣40)]
解得x=80(舍).
⑤B为【A,P】的好点
20﹣(﹣40)=2(20﹣x)
∴x=﹣10
t=[20﹣(﹣10)]÷2=15(秒);
此种情况点P的位置与②中重合,即点P为AB中点.
综上可知,当t为10秒、15秒或20秒,P、A和B中恰有一个点为其余两点的好点.
15.【新知理解】如图①,点C在线段AB上,图中的三条线段AB、AC和BC.若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“蓝青点”.
(1)填空:线段的中点 是 这条线段的“蓝青点”;(填“是”或“不是”)
【问题解决】
(2)如图②,点A和B在数轴上表示的数分别是﹣20和40,点C是线段AB的“蓝青点”,求点C在数轴上表示的数.
【应用拓展】
(3)在(2)的条件下,动点P从点A出发,以每秒2个单位长度的速度沿AB向点B匀速运动;动点Q从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.点P、Q同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为t秒,当t为何值时,A、P、Q三点中,其中一点恰好是另外两点为端点的线段的“蓝青点”?(直接写出答案).
【思路点拔】(1)由题意得AB=2AC=2BC,即可判断点C是AB的“蓝青点”.
(2)先设点C表示的数为x,然后分三种情况:AB=2AC、BC=2AC和AC=2BC,建立方程求解即可.
(3)根据题意求出AP、AQ和PQ关于t的表达式,其中PQ的长度分0≤t≤12和12<t≤20两个表达式,然后再由“蓝青点”的定义建立方程求解即可.
【解答】解:(1)根据题意AB=2AC=2BC,所以线段的中点是这条线段的“蓝青点”.
故答案为:是.
(2)设C点表示的数为x,则 AC=x+20,BC=40﹣x,AB=40+20=60,根据“蓝青点”的定义可知:
①当AB=2AC时,有60=2(x+20),则x=10;
②当BC=2AC时,有40﹣x=2(x+20),则x=0;
③当AC=2BC时,有x+20=2(40﹣x),则x=20.
综上,C点表示的数为10或0或20.
(3)由题意得,AP=2t,AQ=60﹣3t,PQ.
若0≤t≤12时,A、P、Q三点中其中一点是其它两点的“蓝青点”,有如下情况:
①当AQ=2AP时,60﹣3t=2×2t,则t;
②当PQ=2AP时,60﹣5t=2×2t,则t;
③当AP=2PQ时,2t=2×(60﹣5t),则t=10.
若12<t≤20时,A、P、Q三点中其中一点是其它两点的“蓝青点”,有如下情况:
①当AQ=2PQ时,60﹣3t=2×(5t﹣60),则t;
②当PQ=2AQ时,5t﹣60=2×(60﹣3t),则,t;
③当AP=2PQ时,2t=2×(5t﹣60),则t=15.
综上,t可能的值为:,,10,,,15.
浙教版七上期中复习—中档题
一.选择题(共6小题)
1.下列说法中正确的是( )
A.有理数与数轴上的点一一对应
B.负数有立方根
C.如果三个有理数的积为正数,那么这三个数中负因数的个数为0
D.若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a≤7.304
2.下列说法中:①立方根等于本身的是﹣1、0、1; ②平方根等于本身的数是0、1;③两个无理数的和一定是无理数; ④实数与数轴上的点是一一对应的;⑤是负分数;其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
3.一个是三位数a放在一个两位数b前面组成一个五位数,则这个五位数可以用代数式表示为( )
A.ab B.1000a+100b
C.100a+1000b D.100a+b
4.下列说法:(1)的系数是;(2)x2+2xy﹣3的常数项是3;(3)﹣2yx2与2x2y是同类项;(4)是三次二项式.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
5.若a2﹣3b=4,则﹣6b+2a2+2012值为( )
A.2008 B.2016 C.2020 D.2004
6.为了求1+7+72+...+72023的值,可令S=1+7+72+...+72023,则7S=7+72+...+72023+72024,因此7S﹣S=72024﹣1,所以.这种方法称为“错位相减法”.请参考以上推理计算:1×21+2×22+3×23+ +9×29=( )
A.213 B.213+2 C.213+4 D.213+8
二.填空题(共2小题)
7.近似数4.50万精确到 位.
8.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.则b= ,若前n个格子中所填整数之和是2023,则n的值是 .
7 a b c ﹣4 1 …
三.解答题(共7小题)
9.计算:
(1);
(2).
10.(1)已知单项式2x2my7与单项式5x6yn﹣8是同类项,求m2﹣3n的值.
(2)已知关于x的多项式mx3﹣3x2+4x+x3+x2﹣nx不含三次项和一次项,求(m﹣n)2的值.
11.已知.
(1)求a0的值;
(2)求a1+a2+a3+a4+a5的值;
(3)求a1+a3+a5的值.
12.数轴是初中数学的一个重要的工具,研究数轴可以发现许多重要的规律.如数轴上的点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
解决问题:现数轴上有一点A表示的数为﹣10,点B表示的数为18,点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒(t>0).
(1)填空:
①A、B两点之间的距离AB= ,线段AB的中点表示的数为 .
②当t= 时,P、Q两点相遇,相遇点所表示的数为 .
(2)求当t为何值时,PQAB.
(3)折叠数轴使点A、P重合,折点记为M,还原后再折叠数轴使点B、P重合,折点记为N,点P在运动过程中,M、N两点间的距离是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长度.
13.如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为8,点P从点A出发以每秒2个单位长度的速度在数轴上向右运动,当点P到达点B后立即返回,再以每秒3个单位长度的速度向左运动.设点P运动时间为t(s).
(1)当t=7时,点P表示的有理数为 ;
(2)当点P运动到AB中点时,t的值为 ;
(3)当点P与原点距离是2个单位长度时,求t的值.
14.阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
又如,表示0的点D到点A的距离是1,到点B的距离是2.那么点D就不是【A,B】的好点,但点D是【B,A】的好点:
知识运用:
(1)如图1,点B是【D,C】的好点吗? (填是或不是);
(2)如图2,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止,当t为何值时,P、A和B中恰有一个点为其余两点的好点?
15.【新知理解】如图①,点C在线段AB上,图中的三条线段AB、AC和BC.若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“蓝青点”.
(1)填空:线段的中点 这条线段的“蓝青点”;(填“是”或“不是”)
【问题解决】
(2)如图②,点A和B在数轴上表示的数分别是﹣20和40,点C是线段AB的“蓝青点”,求点C在数轴上表示的数.
【应用拓展】
(3)在(2)的条件下,动点P从点A出发,以每秒2个单位长度的速度沿AB向点B匀速运动;动点Q从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.点P、Q同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为t秒,当t为何值时,A、P、Q三点中,其中一点恰好是另外两点为端点的线段的“蓝青点”?(直接写出答案).
浙教版七上期中复习—中档题
一.选择题(共6小题)
1.下列说法中正确的是( )
A.有理数与数轴上的点一一对应
B.负数有立方根
C.如果三个有理数的积为正数,那么这三个数中负因数的个数为0
D.若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a≤7.304
【思路点拔】利用实数与数轴的关系,立方根的定义,有理数的乘法,近似数的精确度对各选项分析判断后利用排除法求解.
【解答】解:∵数轴上的点有的表示有理数,有的表示无理数,而有理数和无理数统称为实数,
∴实数与数轴上的点一一对应,
故A错误,不符合题意;
负数有立方根,故B正确,符合题意;
如果三个有理数的积为正数,那么这三个数中负因数的个数为0或三个,
故C错误,不符合题意;
若数a由四舍五入法得到近似数为7.30,则数a的范围是:7.295≤a<7.305.
故D错误,不符合题意.
故选:B.
2.下列说法中:①立方根等于本身的是﹣1、0、1; ②平方根等于本身的数是0、1;③两个无理数的和一定是无理数; ④实数与数轴上的点是一一对应的;⑤是负分数;其中正确的个数是( )
A.0个 B.1个 C.2个 D.3个
【思路点拔】根据立方根、平方根、无理数以及实数和数轴的概念逐一判断,即可得到答案.
【解答】解:①立方根等于本身的是﹣1、0、1,原说法正确;
②平方根等于本身的数是0,原说法错误;
③(﹣π)+π=0,即两个无理数的和不一定是无理数,原说法错误;
④实数与数轴上的点是一一对应的,原说法正确;
⑤是无理数,原说法错误;
∴正确的说法有①④,共2个,
故选:C.
3.一个是三位数a放在一个两位数b前面组成一个五位数,则这个五位数可以用代数式表示为( )
A.ab B.1000a+100b
C.100a+1000b D.100a+b
【思路点拔】a原来的最高位是千位,现在的最高位是十万位,扩大了100倍,b不变.
【解答】解:三位数a放在一个两位数b前面相当于a扩大了100倍,那么这个五位数为(100a+b).故选D.
4.下列说法:(1)的系数是;(2)x2+2xy﹣3的常数项是3;(3)﹣2yx2与2x2y是同类项;(4)是三次二项式.其中正确的说法有( )
A.1个 B.2个 C.3个 D.4个
【思路点拔】根据同类项的定义、单项式的系数的定义、多项式的项和次数的定义逐项判断即可.
【解答】解:(1)的系数是,正确;
(2)x2+2xy﹣3的常数项是﹣3,原说法错误;
(3)﹣2yx2与2x2y是同类项,正确;
(4)是三次二项式,正确;
所以正确的有3个,
故选:C.
5.若a2﹣3b=4,则﹣6b+2a2+2012值为( )
A.2008 B.2016 C.2020 D.2004
【思路点拔】将a2﹣3b=4代入原式=2(a2﹣3b)+2012,计算可得.
【解答】解:当a2﹣3b=4时,
原式=2(a2﹣3b)+2012
=2×4+2012
=2020,
故选:C.
6.为了求1+7+72+...+72023的值,可令S=1+7+72+...+72023,则7S=7+72+...+72023+72024,因此7S﹣S=72024﹣1,所以.这种方法称为“错位相减法”.请参考以上推理计算:1×21+2×22+3×23+ +9×29=( )
A.213 B.213+2 C.213+4 D.213+8
【思路点拔】设S=1×21+2×22+3×23+ +9×29,则2S=1×22+2×23+3×24+ +9×29+9×210,两式相减得2S=1×22+2×23+3×24+ +9×29+9×210,再设P=21+22+23+ +9×29,则2P=22+23+24+ +9×29+210,再将两式相减得P=210﹣2,由此即可得出答案.
【解答】解:设S=1×21+2×22+3×23+ +9×29,
∴2S=1×22+2×23+3×24+ +9×29+9×210,
∴2S﹣S=9×210﹣(21+22+23+ +29),
即S=9×210﹣(21+22+23+ +29),
设P=21+22+23+ +29,
∴2P=22+23+24+ +29+210,
∴2P﹣P=210﹣2,
即P=210﹣2,
∴S=9×210﹣210+2=8×210+2=23×210+2=213+2,
∴1×21+2×22+3×23+ +9×29=213+2.
故选:B.
二.填空题(共2小题)
7.近似数4.50万精确到 百 位.
【思路点拔】根据近似数4.50万的最后的尾数0,在百位上,可知近似数4.50万精确到百位.
【解答】解:近似数4.50万精确到百位,
故答案为:百.
8.如图,从左到右在每个小格子中填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.则b= 1 ,若前n个格子中所填整数之和是2023,则n的值是 1517 .
7 a b c ﹣4 1 …
【思路点拔】根据题意得,7+a+b=a+b+c,a+b+c=b+c﹣4,b+c﹣4=c﹣4+1,得c=7,a=﹣4,b=1,得这组数为7,﹣4,1,7,﹣4,1,......,得三个相邻格子中的数之和为7﹣4+1=4,2023÷4=505余3,即可得n=505×3+2=1517.
【解答】解:根据题意得,7+a+b=a+b+c,a+b+c=b+c﹣4,b+c﹣4=c﹣4+1,
∴c=7,a=﹣4,b=1,
∴这组数为7,﹣4,1,7,﹣4,1,......,
∴三个相邻格子中的数之和为7﹣4+1=4,2023÷4=505余3,
∴n=505×3+2=1517.
故答案为:1;1517.
三.解答题(共7小题)
9.计算:
(1);
(2).
【思路点拔】(1)利用乘法分配律计算即可得到结果;
(2)先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.
【解答】解:(1)
=﹣8+21﹣10
=3;
(2)
.
10.(1)已知单项式2x2my7与单项式5x6yn﹣8是同类项,求m2﹣3n的值.
(2)已知关于x的多项式mx3﹣3x2+4x+x3+x2﹣nx不含三次项和一次项,求(m﹣n)2的值.
【思路点拔】(1)根据同类项的定义可得:2m=6,n﹣8=7,从而可得:m=3,n=15,然后代入式子中进行计算即可解答;
(2)先利用合并同类项的法则进行计算,再根据题意可得:m+1=0,4﹣n=0,从而可得m=﹣1,n=4,然后代入式子中进行计算即可解答.
【解答】解:(1)∵单项式2x2my7与单项式5x6yn﹣8是同类项,
∴2m=6,n﹣8=7,
解得:m=3,n=15,
∴m2﹣3n=32﹣3×15=9﹣45=﹣36;
(2)mx3﹣3x2+4x+x3+x2﹣nx=(m+1)x3﹣2x2+(4﹣n)x,
由题意得:m+1=0,4﹣n=0,
解得:m=﹣1,n=4,
∴(m﹣n)2=(﹣1﹣4)2=25.
11.已知.
(1)求a0的值;
(2)求a1+a2+a3+a4+a5的值;
(3)求a1+a3+a5的值.
【思路点拔】(1)把x=0代入代数式计算即可;
(2)把x=1代入代数式结合(1)中的结果即可求出a1+a2+a3+a4+a5的值;
(3)把x=﹣1代入代数式结合(1)(2)中的结果即可求出a1+a3+a5的值.
【解答】解:(1)令x=0,则;
(2)令x=1,则25=32,
所以a1+a2+a3+a4+a5=32﹣(﹣1)=32+1=33;
(3)令x=﹣1,则,
所以﹣a5+a4﹣a3+a2﹣a1=﹣1024﹣(﹣1)=﹣1023①,
由(2)知a1+a2+a3+a4+a5=33②,
②﹣①,得2a1+2a3+2a5=1056,
所以a1+a3+a5=528.
12.数轴是初中数学的一个重要的工具,研究数轴可以发现许多重要的规律.如数轴上的点A、点B表示的数分别为a、b,则A、B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为.
解决问题:现数轴上有一点A表示的数为﹣10,点B表示的数为18,点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒1个单位长度的速度向左匀速运动,设运动时间为t秒(t>0).
(1)填空:
①A、B两点之间的距离AB= 28 ,线段AB的中点表示的数为 4 .
②当t= 时,P、Q两点相遇,相遇点所表示的数为 .
(2)求当t为何值时,PQAB.
(3)折叠数轴使点A、P重合,折点记为M,还原后再折叠数轴使点B、P重合,折点记为N,点P在运动过程中,M、N两点间的距离是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长度.
【思路点拔】(1)①根据已知可得AB=|﹣10﹣18|=28,中点表示的数为4;
②运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,可得﹣10+2t=18﹣t,解得t,故当t时,P、Q两点相遇,相遇点所表示的数为;
(2)运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,可得|﹣10+2t﹣(18﹣t)|28,解得t=14或t;
(3)根据题意,点M是AP的中点,N是BP的中点,得点M表示的数为﹣10+t,点N表示的数为4+t,从而MN=|﹣10+t﹣(4+t)|=14.
【解答】解:(1)①由题意可得,
A、B两点之间的距离AB=|﹣10﹣18|=28,线段AB的中点表示的数为4,
故答案为:28,4;
②运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,
∴﹣10+2t=18﹣t,
解得t,
此时﹣10+2t=﹣10+2,
∴当t时,P、Q两点相遇,相遇点所表示的数为,
故答案为:,;
(2)运动后P表示的数是﹣10+2t,Q表示的数是18﹣t,
∴|﹣10+2t﹣(18﹣t)|28,
解得t=14或t;
∴当t=14或t时,PQAB;
(3)点P在运动过程中,线段MN的长度不发生变化,理由如下:
根据题意,点M是AP的中点,N是BP的中点,
∴点M表示的数为:10+t,点N表示的数为:4+t,
∴MN=|﹣10+t﹣(4+t)|=14,
∴点P在运动过程中,线段MN的长度不发生变化.
13.如图,数轴上点A表示的有理数为﹣4,点B表示的有理数为8,点P从点A出发以每秒2个单位长度的速度在数轴上向右运动,当点P到达点B后立即返回,再以每秒3个单位长度的速度向左运动.设点P运动时间为t(s).
(1)当t=7时,点P表示的有理数为 5 ;
(2)当点P运动到AB中点时,t的值为 3或8 ;
(3)当点P与原点距离是2个单位长度时,求t的值.
【思路点拔】(1)当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),列方程求解.
(2)用含t代数式表示点P所表示的数,使其等于8,进而求解.
(3)点P到原点距离为2的数为2或﹣2,分类讨论点P从A向B和从B向A运动时点P表示的数为±2,进而求解.
(4)根据BP=3AP求出点P所表示的数,然后列方程求解.
【解答】解:(1)点P从A向B运动到B用时(4+8)÷2=6(s),
当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),
当t=7时,8﹣3(t﹣6)=8﹣3=5,
故答案为:5;
(2)当点P运动到AB中点时,点P表示的数为:2,
当点P从A向B运动到AB中点时,
由题意得﹣4+2t=2,
解得t=3.
当点P从B向A运动时,点P所表示的数为8﹣3(t﹣6),
由题意得8﹣3(t﹣6)=2,
解得t=8.
故答案为:3或8;
(3)当点P表示的数为2或﹣2时满足题意,
解﹣4+2t=﹣2得t=1,
解﹣4+2t=2得t=3,
解8﹣3(t﹣6)=2得t=8,
解8﹣3(t﹣6)=﹣2得t.
故答案为:1或3或8或.
14.阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是【A,B】的好点.
例如,如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点.
又如,表示0的点D到点A的距离是1,到点B的距离是2.那么点D就不是【A,B】的好点,但点D是【B,A】的好点:
知识运用:
(1)如图1,点B是【D,C】的好点吗? 是 (填是或不是);
(2)如图2,A、B为数轴上两点,点A所表示的数为﹣40,点B所表示的数为20.现有一只电子蚂蚁P从点B出发,以2个单位每秒的速度向左运动,到达点A停止,当t为何值时,P、A和B中恰有一个点为其余两点的好点?
【思路点拔】(1)根据定义计算BD、BC,验证是否具有BD=2BC即可;
(2)设点P表示的数为x,分情况讨论:①P为【A,B】的好点;②A为【B,P】的好点;③P为【B,A】的好点;④A为【P,B】的好点;⑤B为【A,P】的好点.
【解答】解:(1)∵BD=2,BC=1,BD=2BC
∴点B是【D,C】的好点.
故答案为:是;
(2)设点P表示的数为x,分以下几种情况:
①P为【A,B】的好点
由题意,得x﹣(﹣40)=2(20﹣x),
解得x=0,
t=20÷2=10(秒);
②A为【B,P】的好点
由题意,得20﹣(﹣40)=2[x﹣(﹣40)],
解得x=﹣10,
t=[20﹣(﹣10)]÷2=15(秒);
③P为【B,A】的好点
由题意,得20﹣x=2[x﹣(﹣40)],
解得x=﹣20,
t=[20﹣(﹣20)]÷2=20(秒);
④A为【P,B】的好点
由题意得x﹣(﹣40)=2[20﹣(﹣40)]
解得x=80(舍).
⑤B为【A,P】的好点
20﹣(﹣40)=2(20﹣x)
∴x=﹣10
t=[20﹣(﹣10)]÷2=15(秒);
此种情况点P的位置与②中重合,即点P为AB中点.
综上可知,当t为10秒、15秒或20秒,P、A和B中恰有一个点为其余两点的好点.
15.【新知理解】如图①,点C在线段AB上,图中的三条线段AB、AC和BC.若其中一条线段的长度是另外一条线段长度的2倍,则称点C是线段AB的“蓝青点”.
(1)填空:线段的中点 是 这条线段的“蓝青点”;(填“是”或“不是”)
【问题解决】
(2)如图②,点A和B在数轴上表示的数分别是﹣20和40,点C是线段AB的“蓝青点”,求点C在数轴上表示的数.
【应用拓展】
(3)在(2)的条件下,动点P从点A出发,以每秒2个单位长度的速度沿AB向点B匀速运动;动点Q从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.点P、Q同时出发,当其中一点到达终点时,两个点运动同时停止,设运动的时间为t秒,当t为何值时,A、P、Q三点中,其中一点恰好是另外两点为端点的线段的“蓝青点”?(直接写出答案).
【思路点拔】(1)由题意得AB=2AC=2BC,即可判断点C是AB的“蓝青点”.
(2)先设点C表示的数为x,然后分三种情况:AB=2AC、BC=2AC和AC=2BC,建立方程求解即可.
(3)根据题意求出AP、AQ和PQ关于t的表达式,其中PQ的长度分0≤t≤12和12<t≤20两个表达式,然后再由“蓝青点”的定义建立方程求解即可.
【解答】解:(1)根据题意AB=2AC=2BC,所以线段的中点是这条线段的“蓝青点”.
故答案为:是.
(2)设C点表示的数为x,则 AC=x+20,BC=40﹣x,AB=40+20=60,根据“蓝青点”的定义可知:
①当AB=2AC时,有60=2(x+20),则x=10;
②当BC=2AC时,有40﹣x=2(x+20),则x=0;
③当AC=2BC时,有x+20=2(40﹣x),则x=20.
综上,C点表示的数为10或0或20.
(3)由题意得,AP=2t,AQ=60﹣3t,PQ.
若0≤t≤12时,A、P、Q三点中其中一点是其它两点的“蓝青点”,有如下情况:
①当AQ=2AP时,60﹣3t=2×2t,则t;
②当PQ=2AP时,60﹣5t=2×2t,则t;
③当AP=2PQ时,2t=2×(60﹣5t),则t=10.
若12<t≤20时,A、P、Q三点中其中一点是其它两点的“蓝青点”,有如下情况:
①当AQ=2PQ时,60﹣3t=2×(5t﹣60),则t;
②当PQ=2AQ时,5t﹣60=2×(60﹣3t),则,t;
③当AP=2PQ时,2t=2×(5t﹣60),则t=15.
综上,t可能的值为:,,10,,,15.
同课章节目录
