第二十一章一元二次方程典型例题与跟踪训练(含解析)
文档属性
| 名称 | 第二十一章一元二次方程典型例题与跟踪训练(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 926.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-09 09:21:16 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第二十一章一元二次方程典型例题与跟踪训练-数学九年级上册人教版
一、单选题
1.在下列方程中,是一元二次方程的是( )
A. B.(是已知的数)
C. D.
2.不解方程,请你判断一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
3.如图,从一块长方形铁片中间截去一个小长方形,使剩下部分四周的宽度都等于,且小长方形的面积是原来长方形面积的一半,则的值为( )
A. B. C.或 D.或
4.用配方法解一元二次方程 ,下面的配方正确的是( )
A. B. C. D.
5.若关于x的一元二次方程有不相等实数根,则k的取值范围是( )
A. B. C.且 D.且
6.已知是方程的两根,则,分别为( )
A. B. C. D.
7.学校“自然之美”研究小组在野外考查时了发现一种植物的生长规律,即植物的个主干上长出个枝干,每个枝干又长出个小分支,现在一个主干上有主干、枝干、小分支数量之和为,根据题意,下列方程正确的是( )
A. B.
C. D.
8.如图,一矩形草坪的长为25米,宽为12米,在草坪上有两条互相垂直且宽度相等的矩形小路(阴影部分),非阴影部分的面积是230平方米.设小路宽x米,则根据题意,可列方程( )
A. B.
C. D.
二、填空题
9.已知是一元二次方程的一个解,则m的值为 .
10.关于的一元二次方程有实数根,则的取值范围是 .
11.若m是一元二次方程的一个实数根,则的值是 .
12.若一个三角形两条边长为2和4,第三边长满足方程,则此三角形的周长为 .
13.若的两个实数根为和,那么关于x的一元二次方程的解为 .
14.的两边、的长是关于的方程的两个实数根.当为 时,四边形是菱形.
15.去年8月以来,非洲猪瘟疫情在某国横行,今年猪瘟疫情发生势头明显减缓.假如有一头猪患病,经过两轮传染后共有64头猪患病.每轮传染中平均每头患病猪传染了 头健康猪.
16.对于两个不相等的实数.我们规定符号表示中的较大值,如:.按照这个规定,若,则的值是 .
三、解答题
17.解方程:
(1)
(2)
18.已知关于x的一元二次方程的一个根为,求m的值和方程的另一个根.
19.某童装专卖店在销售中发现,一款童装每件的进价为80元,当销售单价为120元时,每天可售出20件.为了迎接国庆节,该专卖店决定采取适当的降价措施,以最大限度地扩大销售量,减少库存,增加利润.据测算,每件童装每降价1元,平均每天可多售出2件,当每件童装降价多少元时,平均每天盈利1200元?
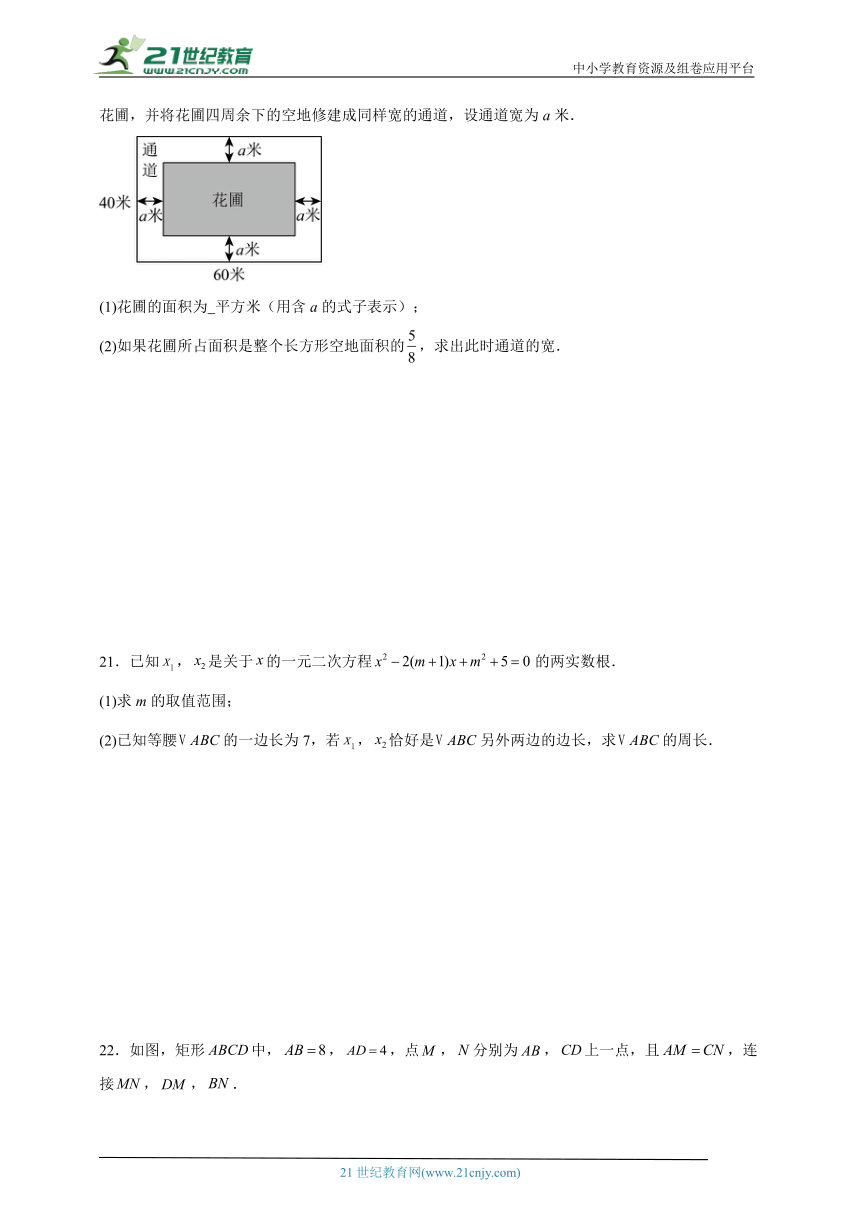
20.如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)花圃的面积为 平方米(用含a的式子表示);
(2)如果花圃所占面积是整个长方形空地面积的,求出此时通道的宽.
21.已知,是关于的一元二次方程的两实数根.
(1)求m的取值范围;
(2)已知等腰的一边长为7,若,恰好是另外两边的边长,求的周长.
22.如图,矩形中,,,点,分别为,上一点,且,连接,,.
(1)当时,四边形是________(填序号);
①菱形;②矩形;③正方形.
(2)若四边形是矩形,求的长;
(3)若以为对角线的正方形的面积为时,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B B A C C C B
1.C
【分析】本题考查了一元二次方程的概念,根据一元二次方程的概念“含有一个未知数,未知数的最高次数为2次的整数方程”进行判定即可求解.
【详解】解:A、,
,不是一元二次方程,不符合题意;
B、,当时,不是一元二次方程,不符合题意;
C、,含有一个未知数,未知数的最高次数是2,等号两边都是整式,是一元二次方程,符合题意;
D、中,不是整式,不是一元二次方程,不符合题意;
故选:C .
2.B
【分析】本题考查一元二次方程根的判别式.熟练掌握判别式与根的个数的关系,是解题的关键.求出判别式的值,进行判断即可.
【详解】解:∵,
∴,
∴方程有两个不相等的实数根,
故选B.
3.B
【分析】本题考查了一元二次方程的应用,由题意可得,小长方形的长为,宽为,进而根据小长方形的面积是原来长方形面积的一半列出方程即可求解,正确列出方程是解题的关键.
【详解】解:由题意可得,小长方形的长为,宽为,
则,
整理得,,
解得,(不合,舍去),
∴,
故选:.
4.A
【分析】本题考查了配方法,移项、再方程两边同时加上即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴,
∴,
即,
故选:.
5.C
【分析】本题考查了一元二次方程的根的判别式和一元二次方程的定义,关键是熟练掌握:当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根.根据二次项系数不为0和判别式进行解答即可.
【详解】根据题意得:且,
解得:且.
故选:C
6.C
【分析】本题考查了一元二次方程根与系数的关系,若为方程的两个根,则与系数的关系式:,.直接根据根与系数的关系求解即可.
【详解】解:是方程的两根,
,
,,
故选:C.
7.C
【分析】本题考查了一元二次方程的应用,根据题意列出方程即可,理解题意是解题的关键.
【详解】解:由题意可得,,
故选:.
8.B
【分析】本题考查列一元二次方程解决实际问题.将两条小路平移到草坪的边上,设小路宽x米,则非阴影部分为一个矩形,其长为米,宽为米,根据“非阴影部分的面积是230平方米”即可列出方程.
【详解】解:设小路宽x米,根据题意,得
故选:B
9.
【分析】本题考查了一元二次方程的解,把代入方程计算即可求解,掌握一元二次方程解的定义是解题的关键.
【详解】解:∵是一元二次方程的一个解,
∴,
∴,
故答案为:.
10.且
【分析】本题考查了一元二次方程的定义及根的判别式,当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根,据此即可解答,掌握一元二次方程的定义及根的判别式是解题的关键.
【详解】解:∵一元二次方程有实数根,
∴即,且,
即有,
解得,
∴的取值范围是且,
故答案为:且.
11.2024
【分析】本题考查的知识点是一元二次方程的解、已知式子的值,求代数式的值,解题关键是根据题意得到,再代入求值.
【详解】解:由题意得,,
∴,
∴,
故答案为:2024.
12.11
【分析】本题考查了因式分解解一元二次方程,三角形三边关系,先解一元二次方程得出或,再根据三角形三边关系判断即可得出答案.
【详解】解:∵,
∴,
则或,
解得:或,
当时,三边,不能构成三角形;
当时,此三角形的周长为,
故答案为:11.
13.或
【分析】本题考查了解一元二次方程,熟练掌握换元法是解题关键.令可将方程化成可得或,由此即可得.
【详解】解:令,
则方程可化成为方程,
∵的两个实数根为和,
方程的两个实数根为和3,
或,
解得或,
故答案为:或.
14.
【分析】本题考查了根与系数的关系和平行四边形和菱形的性质.先根据菱形的性质得到,则根据根的判别式的意义得到,然后解关于m的方程即可解题.
【详解】解:由题可得:,
则方程有两个相等的实数根,
∴,
解得:,
故答案为:.
15.7
【分析】本题主要考查了一元二次方程的实际应用,设每轮传染中平均每头患病猪传染了x头健康猪,则第一轮传染后有头猪被感染,第二轮又要感染头猪,据此列出方程求解即可.
【详解】解:设每轮传染中平均每头患病猪传染了x头健康猪,
由题意得,,
整理得,
解得或(舍去),
∴每轮传染中平均每头患病猪传染了7头健康猪,
故答案为:7.
16.或
【分析】本题考查了解一元二次方程因式分解法,配方法,实数的运算,实数大小比较,分两种情况:当时,即时;当时,即时;然后根据定义的新运算列出方程,解方程即可解答.
【详解】解:分两种情况:
当时,即时,
,
,
整理得:,
,
或,
,舍去;
当时,即时,
,
,
整理得:,
,
,
,
,
或,
,舍去,;
综上所述:或,
故答案为:或.
17.(1),
(2),
【分析】本题考查的是一元二次方程的解法,掌握解方程的方法是关键;
(1)把方程化为,再利用配方法解方程即可;
(2)把方程化为,再利用因式分解的方法解方程即可.
【详解】(1)解:,
∴,
∴,
∴,
解得:,;
(2)解:,
∴,
∴,
∴,
∴或,
解得:,;
18.,方程的另一个根为3
【分析】本题考查了一元二次方程的根、根与系数的关系等知识点,把代入方程,求出的值,再设方程的另一个根为,根据根与系数的关系求出的值即可.
【详解】是方程的一个根,
,
;
设方程的另一个根为,
,
.
,方程的另一个根为3.
19.20元
【分析】本题主要考查了一元二次方程的应用,先设每件童装降价元,可表示每天可销售量,每件利润,再根据总利润等于1200列出方程,求出解即可.
【详解】解:设每件童装降价元,则每天可销售件,每件盈利元,
则根据题意,得:.
解得:,,
∵要最大限度地扩大销售量,增加利润,
∴,
答:当每件童装降价20元时,平均每天盈利1200元.
20.(1)
(2)此时通道的宽为5米.
【分析】本题主要考查了一元二次方程的实际应用,多项式乘法与图形面积:
(1)长方形花圃的长为米,宽为米,据此根据长方形面积计算公式求解即可;
(2)根据(1)所求结合题意建立方程求解即可.
【详解】(1)解:由题意得,长方形花圃的长为米,宽为米,
∴花圃的面积为平方米,
故答案为:;
(2)解:由题意得,,
整理得,
解得或(舍去),
答:此时通道的宽为5米.
21.(1);
(2)这个三角形的周长为17
【分析】本题考查了一元二次方程根的判别式,三角形三边关系,等腰三角形的性质,能利用分类讨论的思想求解是解题的关键.
(1)根据判别式的意义可得;
(2)分类讨论:分当腰长为7或当7为等腰三角形的底边两种情况讨论,求出值,再由三角形的三边关系即可得出结论.
【详解】(1)解:根据题意得,
解得;
(2)解:当腰长为7时,则是一元二次方程的一个解,
把代入方程得,
整理得,解得,,
当时,,解得,而,故舍去;
当时,,解得,则三角形周长为;
当7为等腰三角形的底边时,则,所以,方程化为,
解得,则,故舍去,
综上所述,这个三角形的周长为17.
22.(1)①
(2)4
(3)或
【分析】(1)由矩形的性质得,,,而,所以,则四边形为平行四边形,再根据勾股定理求得,则,即可证明四边形为菱形;
(2)四边形矩形则,由,求得;
(3)由以为对角线的正方形的面积为计算出,作于点,则,,所以,由勾股定理得,求得或,于是得到问题的答案.
【详解】(1)解:如图1,
四边形是矩形,,,
,,,
,
,
,
四边形为平行四边形,
,
,
四边形为菱形.
故答案为:①;
(2)解:如图2,
∵四边形矩形,
,
,
∴,
∵,
∴.
(3)解:如图3,
以为对角线的正方形是正方形,连接,
,,
,
,
作于点,则,
四边形是矩形,
,,
,
,
,
,
解得或,
当或,以为对角线的正方形的面积为,
故答案为:或.
【点睛】此题重点考查矩形的判定与性质、菱形的判定、正方形的判定、勾股定理、一元二次方程的解法等知识与方法,证明四边形为平行四边形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十一章一元二次方程典型例题与跟踪训练-数学九年级上册人教版
一、单选题
1.在下列方程中,是一元二次方程的是( )
A. B.(是已知的数)
C. D.
2.不解方程,请你判断一元二次方程的根的情况为( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.没有实数根 D.无法确定
3.如图,从一块长方形铁片中间截去一个小长方形,使剩下部分四周的宽度都等于,且小长方形的面积是原来长方形面积的一半,则的值为( )
A. B. C.或 D.或
4.用配方法解一元二次方程 ,下面的配方正确的是( )
A. B. C. D.
5.若关于x的一元二次方程有不相等实数根,则k的取值范围是( )
A. B. C.且 D.且
6.已知是方程的两根,则,分别为( )
A. B. C. D.
7.学校“自然之美”研究小组在野外考查时了发现一种植物的生长规律,即植物的个主干上长出个枝干,每个枝干又长出个小分支,现在一个主干上有主干、枝干、小分支数量之和为,根据题意,下列方程正确的是( )
A. B.
C. D.
8.如图,一矩形草坪的长为25米,宽为12米,在草坪上有两条互相垂直且宽度相等的矩形小路(阴影部分),非阴影部分的面积是230平方米.设小路宽x米,则根据题意,可列方程( )
A. B.
C. D.
二、填空题
9.已知是一元二次方程的一个解,则m的值为 .
10.关于的一元二次方程有实数根,则的取值范围是 .
11.若m是一元二次方程的一个实数根,则的值是 .
12.若一个三角形两条边长为2和4,第三边长满足方程,则此三角形的周长为 .
13.若的两个实数根为和,那么关于x的一元二次方程的解为 .
14.的两边、的长是关于的方程的两个实数根.当为 时,四边形是菱形.
15.去年8月以来,非洲猪瘟疫情在某国横行,今年猪瘟疫情发生势头明显减缓.假如有一头猪患病,经过两轮传染后共有64头猪患病.每轮传染中平均每头患病猪传染了 头健康猪.
16.对于两个不相等的实数.我们规定符号表示中的较大值,如:.按照这个规定,若,则的值是 .
三、解答题
17.解方程:
(1)
(2)
18.已知关于x的一元二次方程的一个根为,求m的值和方程的另一个根.
19.某童装专卖店在销售中发现,一款童装每件的进价为80元,当销售单价为120元时,每天可售出20件.为了迎接国庆节,该专卖店决定采取适当的降价措施,以最大限度地扩大销售量,减少库存,增加利润.据测算,每件童装每降价1元,平均每天可多售出2件,当每件童装降价多少元时,平均每天盈利1200元?
20.如图,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为a米.
(1)花圃的面积为 平方米(用含a的式子表示);
(2)如果花圃所占面积是整个长方形空地面积的,求出此时通道的宽.
21.已知,是关于的一元二次方程的两实数根.
(1)求m的取值范围;
(2)已知等腰的一边长为7,若,恰好是另外两边的边长,求的周长.
22.如图,矩形中,,,点,分别为,上一点,且,连接,,.
(1)当时,四边形是________(填序号);
①菱形;②矩形;③正方形.
(2)若四边形是矩形,求的长;
(3)若以为对角线的正方形的面积为时,求的长.
参考答案:
题号 1 2 3 4 5 6 7 8
答案 C B B A C C C B
1.C
【分析】本题考查了一元二次方程的概念,根据一元二次方程的概念“含有一个未知数,未知数的最高次数为2次的整数方程”进行判定即可求解.
【详解】解:A、,
,不是一元二次方程,不符合题意;
B、,当时,不是一元二次方程,不符合题意;
C、,含有一个未知数,未知数的最高次数是2,等号两边都是整式,是一元二次方程,符合题意;
D、中,不是整式,不是一元二次方程,不符合题意;
故选:C .
2.B
【分析】本题考查一元二次方程根的判别式.熟练掌握判别式与根的个数的关系,是解题的关键.求出判别式的值,进行判断即可.
【详解】解:∵,
∴,
∴方程有两个不相等的实数根,
故选B.
3.B
【分析】本题考查了一元二次方程的应用,由题意可得,小长方形的长为,宽为,进而根据小长方形的面积是原来长方形面积的一半列出方程即可求解,正确列出方程是解题的关键.
【详解】解:由题意可得,小长方形的长为,宽为,
则,
整理得,,
解得,(不合,舍去),
∴,
故选:.
4.A
【分析】本题考查了配方法,移项、再方程两边同时加上即可求解,掌握配方法是解题的关键.
【详解】解:∵,
∴,
∴,
即,
故选:.
5.C
【分析】本题考查了一元二次方程的根的判别式和一元二次方程的定义,关键是熟练掌握:当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根.根据二次项系数不为0和判别式进行解答即可.
【详解】根据题意得:且,
解得:且.
故选:C
6.C
【分析】本题考查了一元二次方程根与系数的关系,若为方程的两个根,则与系数的关系式:,.直接根据根与系数的关系求解即可.
【详解】解:是方程的两根,
,
,,
故选:C.
7.C
【分析】本题考查了一元二次方程的应用,根据题意列出方程即可,理解题意是解题的关键.
【详解】解:由题意可得,,
故选:.
8.B
【分析】本题考查列一元二次方程解决实际问题.将两条小路平移到草坪的边上,设小路宽x米,则非阴影部分为一个矩形,其长为米,宽为米,根据“非阴影部分的面积是230平方米”即可列出方程.
【详解】解:设小路宽x米,根据题意,得
故选:B
9.
【分析】本题考查了一元二次方程的解,把代入方程计算即可求解,掌握一元二次方程解的定义是解题的关键.
【详解】解:∵是一元二次方程的一个解,
∴,
∴,
故答案为:.
10.且
【分析】本题考查了一元二次方程的定义及根的判别式,当,方程有两个不相等的实数根;当,方程有两个相等的实数根;当,方程没有实数根,据此即可解答,掌握一元二次方程的定义及根的判别式是解题的关键.
【详解】解:∵一元二次方程有实数根,
∴即,且,
即有,
解得,
∴的取值范围是且,
故答案为:且.
11.2024
【分析】本题考查的知识点是一元二次方程的解、已知式子的值,求代数式的值,解题关键是根据题意得到,再代入求值.
【详解】解:由题意得,,
∴,
∴,
故答案为:2024.
12.11
【分析】本题考查了因式分解解一元二次方程,三角形三边关系,先解一元二次方程得出或,再根据三角形三边关系判断即可得出答案.
【详解】解:∵,
∴,
则或,
解得:或,
当时,三边,不能构成三角形;
当时,此三角形的周长为,
故答案为:11.
13.或
【分析】本题考查了解一元二次方程,熟练掌握换元法是解题关键.令可将方程化成可得或,由此即可得.
【详解】解:令,
则方程可化成为方程,
∵的两个实数根为和,
方程的两个实数根为和3,
或,
解得或,
故答案为:或.
14.
【分析】本题考查了根与系数的关系和平行四边形和菱形的性质.先根据菱形的性质得到,则根据根的判别式的意义得到,然后解关于m的方程即可解题.
【详解】解:由题可得:,
则方程有两个相等的实数根,
∴,
解得:,
故答案为:.
15.7
【分析】本题主要考查了一元二次方程的实际应用,设每轮传染中平均每头患病猪传染了x头健康猪,则第一轮传染后有头猪被感染,第二轮又要感染头猪,据此列出方程求解即可.
【详解】解:设每轮传染中平均每头患病猪传染了x头健康猪,
由题意得,,
整理得,
解得或(舍去),
∴每轮传染中平均每头患病猪传染了7头健康猪,
故答案为:7.
16.或
【分析】本题考查了解一元二次方程因式分解法,配方法,实数的运算,实数大小比较,分两种情况:当时,即时;当时,即时;然后根据定义的新运算列出方程,解方程即可解答.
【详解】解:分两种情况:
当时,即时,
,
,
整理得:,
,
或,
,舍去;
当时,即时,
,
,
整理得:,
,
,
,
,
或,
,舍去,;
综上所述:或,
故答案为:或.
17.(1),
(2),
【分析】本题考查的是一元二次方程的解法,掌握解方程的方法是关键;
(1)把方程化为,再利用配方法解方程即可;
(2)把方程化为,再利用因式分解的方法解方程即可.
【详解】(1)解:,
∴,
∴,
∴,
解得:,;
(2)解:,
∴,
∴,
∴,
∴或,
解得:,;
18.,方程的另一个根为3
【分析】本题考查了一元二次方程的根、根与系数的关系等知识点,把代入方程,求出的值,再设方程的另一个根为,根据根与系数的关系求出的值即可.
【详解】是方程的一个根,
,
;
设方程的另一个根为,
,
.
,方程的另一个根为3.
19.20元
【分析】本题主要考查了一元二次方程的应用,先设每件童装降价元,可表示每天可销售量,每件利润,再根据总利润等于1200列出方程,求出解即可.
【详解】解:设每件童装降价元,则每天可销售件,每件盈利元,
则根据题意,得:.
解得:,,
∵要最大限度地扩大销售量,增加利润,
∴,
答:当每件童装降价20元时,平均每天盈利1200元.
20.(1)
(2)此时通道的宽为5米.
【分析】本题主要考查了一元二次方程的实际应用,多项式乘法与图形面积:
(1)长方形花圃的长为米,宽为米,据此根据长方形面积计算公式求解即可;
(2)根据(1)所求结合题意建立方程求解即可.
【详解】(1)解:由题意得,长方形花圃的长为米,宽为米,
∴花圃的面积为平方米,
故答案为:;
(2)解:由题意得,,
整理得,
解得或(舍去),
答:此时通道的宽为5米.
21.(1);
(2)这个三角形的周长为17
【分析】本题考查了一元二次方程根的判别式,三角形三边关系,等腰三角形的性质,能利用分类讨论的思想求解是解题的关键.
(1)根据判别式的意义可得;
(2)分类讨论:分当腰长为7或当7为等腰三角形的底边两种情况讨论,求出值,再由三角形的三边关系即可得出结论.
【详解】(1)解:根据题意得,
解得;
(2)解:当腰长为7时,则是一元二次方程的一个解,
把代入方程得,
整理得,解得,,
当时,,解得,而,故舍去;
当时,,解得,则三角形周长为;
当7为等腰三角形的底边时,则,所以,方程化为,
解得,则,故舍去,
综上所述,这个三角形的周长为17.
22.(1)①
(2)4
(3)或
【分析】(1)由矩形的性质得,,,而,所以,则四边形为平行四边形,再根据勾股定理求得,则,即可证明四边形为菱形;
(2)四边形矩形则,由,求得;
(3)由以为对角线的正方形的面积为计算出,作于点,则,,所以,由勾股定理得,求得或,于是得到问题的答案.
【详解】(1)解:如图1,
四边形是矩形,,,
,,,
,
,
,
四边形为平行四边形,
,
,
四边形为菱形.
故答案为:①;
(2)解:如图2,
∵四边形矩形,
,
,
∴,
∵,
∴.
(3)解:如图3,
以为对角线的正方形是正方形,连接,
,,
,
,
作于点,则,
四边形是矩形,
,,
,
,
,
,
解得或,
当或,以为对角线的正方形的面积为,
故答案为:或.
【点睛】此题重点考查矩形的判定与性质、菱形的判定、正方形的判定、勾股定理、一元二次方程的解法等知识与方法,证明四边形为平行四边形是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
