第5单元圆应用题专项突破-数学六年级上册人教版(含解析)
文档属性
| 名称 | 第5单元圆应用题专项突破-数学六年级上册人教版(含解析) |
|
|
| 格式 | docx | ||
| 文件大小 | 422.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-11-08 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第5单元圆应用题专项突破-数学六年级上册人教版
一、解答题
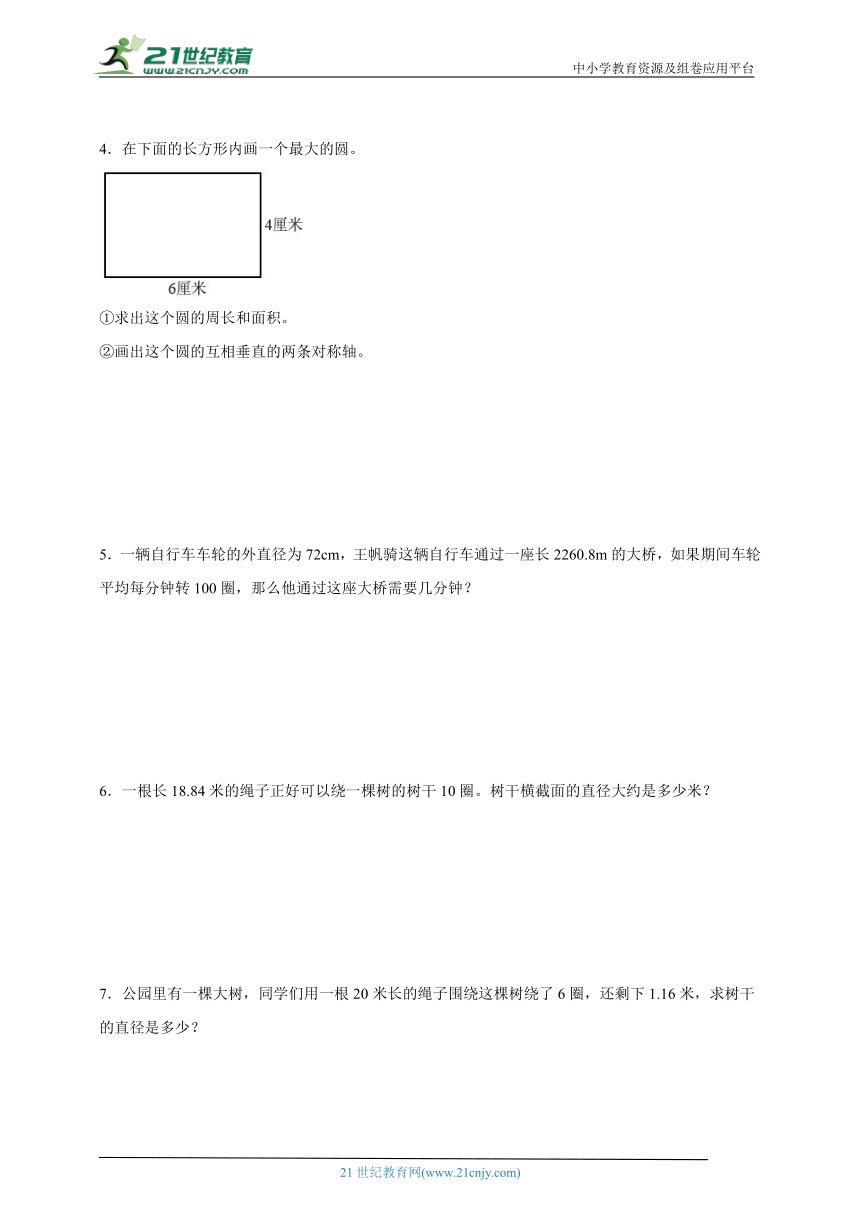
1.在探索圆的面积计算公式时,把圆平均分成32等份,将每份剪下后进行拼接,得到一个近似的长方形。图中圆的面积是多少平方厘米?
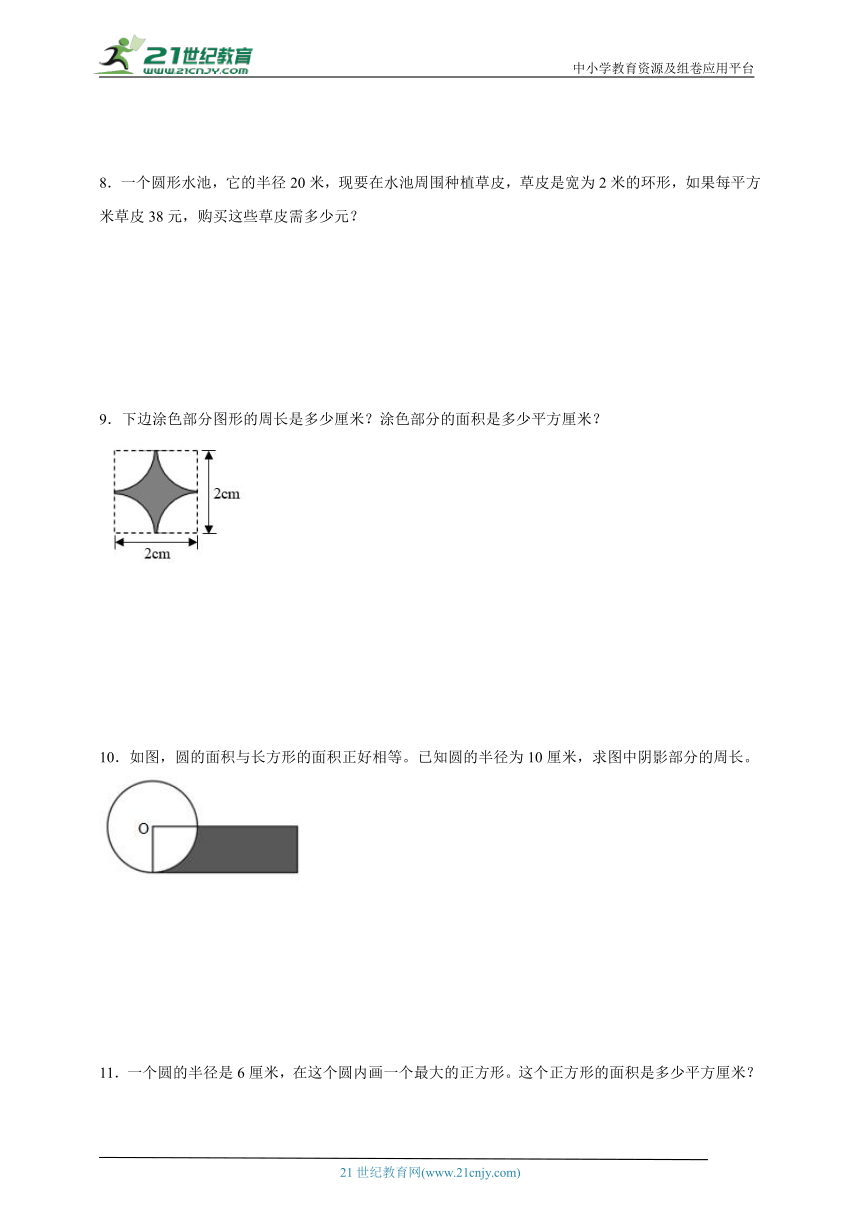
2.如图,这是体育馆运动场的设计图,这个运动场的周长是多少米?面积是多少平方米?
3.人民广场要修建一个圆形花坛,周长是18.84米,花坛面积是多少平方米?若在花坛的周围修一条宽1米的小路,小路的占地面积是多少平方米?
4.在下面的长方形内画一个最大的圆。
①求出这个圆的周长和面积。
②画出这个圆的互相垂直的两条对称轴。
5.一辆自行车车轮的外直径为72cm,王帆骑这辆自行车通过一座长2260.8m的大桥,如果期间车轮平均每分钟转100圈,那么他通过这座大桥需要几分钟?
6.一根长18.84米的绳子正好可以绕一棵树的树干10圈。树干横截面的直径大约是多少米?
7.公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
8.一个圆形水池,它的半径20米,现要在水池周围种植草皮,草皮是宽为2米的环形,如果每平方米草皮38元,购买这些草皮需多少元?
9.下边涂色部分图形的周长是多少厘米?涂色部分的面积是多少平方厘米?
10.如图,圆的面积与长方形的面积正好相等。已知圆的半径为10厘米,求图中阴影部分的周长。
11.一个圆的半径是6厘米,在这个圆内画一个最大的正方形。这个正方形的面积是多少平方厘米?
12.如图,六罐啤酒用一根绳子捆了2圈,不计打结长度,这根绳子长多少厘米?
13.王爷爷靠墙用篱笆围了一个半圆形的鸡舍(如下图),篱笆的长是31.4米,这个鸡舍的占地面积是多少平方米?
14.如图,圆从点A开始,沿着直尺向右滚动一周后到达点B。
(1)请在直尺上标出点B的大概位置(在直尺上描上点,并标注上字母B)。
(2)如果这个圆从点A滚动到点C,请计算出滚动后(含起始状态)所覆盖的面积。(取3.14)
15.用6米长的绳子把一只羊拴在了一块长20米、宽15米的长方形草地中央的木桩上。请问:这只羊能吃到全部的青草吗?请说明理由。(提示:可以先画出示意图进行分析)
16.猫和老鼠在一个直径是50米的圆周上的同一地点向相反方向运动,猫每分钟走21.98米,老鼠每分钟走9.42米。当猫和老鼠第一次相遇时,猫比老鼠多走了多少米?
17.如下图所示,半径为1厘米的小圆盘(娃娃脸)沿着长方形内壁,从A点出发不停滚动(无滑动),最后到原来的位置。小圆盘在B、C、D位置是怎样的,请你计算一下并画出示意图。
18.如图所示:沿半圆形草坪铺一条2米宽的小路,小路的面积是多少平方米?
参考答案:
1.50.24平方厘米
【分析】近似长方形的长是圆周长的一半,那么将12.56厘米乘2,可以求出圆的周长,再将圆的周长除以2再除以圆周率3.14,求出圆的半径。最终,根据S=πr2,代入数据求出这个圆的面积即可。
【详解】12.56×2÷2÷3.14
=12.56÷3.14
=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
答:图中圆的面积是50.24平方厘米。
【点睛】本题考查了圆的周长和面积,解题关键是熟记公式。
2.453.76米;13518.96平方米
【分析】运动场是由两个半圆和一个长方形组成,运动场的周长=一个圆的周长+长方形的两条长,运动场的面积=一个圆的面积+一个长方形的面积。已知圆的半径,可根据求出圆的周长;根据求出圆的面积。已知长方形的长与宽,可根据“长方形的面积=长×宽”求出长方形的面积。
【详解】2×3.14×42+95×2
=6.28×42+190
=263.76+190
=453.76(米)
3.14×+95×(42×2)
=3.14×1764+95×84
=5538.96+7980
=13518.96(平方米)
答:这个运动场的周长是453.76米,面积是13518.96平方米。
【点睛】解决此题的关键是理解运动场的周长包含哪些边的长度,运动场的面积是哪些图形的面积和。
3.28.26平方米;21.98平方米
【分析】根据圆的周长公式C=2πr可知,圆的半径r=C÷π÷2,求出圆形花坛的半径;然后根据圆的面积公式S=πr2,求出花坛的面积;
若在花坛的周围修一条宽1米的小路,求小路的占地面积就是求圆环的面积;内圆的半径r等于圆形花坛的半径,外圆的半径R等于花坛的半径加上1米;然后根据圆环的面积公式S环=π(R2-r2),代入数据计算即可。
【详解】圆形花坛的半径:
18.84÷3.14÷2
=6÷2
=3(米)
花坛的面积:
3.14×32
=3.14×9
=28.26(平方米)
外圆半径:3+1=4(米)
小路的面积:
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(平方米)
答:花坛面积是28.26平方米,小路的占地面积是21.98平方米。
【点睛】本题考查圆的周长、圆的面积、圆环的面积公式的灵活运用,求出内圆和外圆的半径是解题的关键。
4.图形见详解
①12.56厘米;12.56平方厘米;
②见详解
【分析】以长方形的宽为直径的圆是长方形内面积最大的圆,再根据“”和“”求出这个圆的周长和面积,将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,每条直径所在的直线就是圆的对称轴,最后用虚线画出两条互相垂直的对称轴,据此解答。
【详解】①周长:3.14×4=12.56(厘米)
面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
答:这个圆的周长是12.56厘米,面积是12.56平方厘米。
②分析可知:
【点睛】掌握圆的周长和面积计算公式,并根据对称轴的定义画出符合条件的对称轴是解答题目的关键。
5.10分钟
【分析】根据圆的周长=πd,求出车轮转一圈行进的距离,车轮周长×每分钟转动圈数=每分钟行驶距离,统一单位,根据时间=路程÷速度,列式解答即可。
【详解】3.14×72×100=22608(厘米)=226.08(米)
2260.8÷226.08=10(分钟)
答:他通过这座大桥需要10分钟。
【点睛】关键是掌握圆的周长公式,理解速度、时间、路程之间的关系。
6.0.6米
【分析】先用除法表示出树干一圈的长度,再根据“”求出树干横截面的直径,据此解答。
【详解】18.84÷10÷3.14
=1.884÷3.14
=0.6(米)
答:树干横截面的直径大约是0.6米。
【点睛】掌握圆的周长计算公式是解答题目的关键。
7.1米
【分析】已知一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,先用20米减去1.16米,再除以6即可求出一圈的长度,然后根据圆的周长公式求解出树干的直径即可。
【详解】(20-1.16)÷6
=18.84÷6
=3.14(米)
3.14÷3.14=1(米)
答:树干的直径是1米。
【点睛】本题考查了圆周长公式的灵活应用。
8.10022.88元
【分析】由题意可知,小圆半径为20米,环宽为2米,则大圆半径为(20+2)米,利用“”求出环形的面积,最后根据“总价=单价×数量”求出购买草皮需要花费的总钱数,据此解答。
【详解】3.14×[(20+2)2-202]×38
=3.14×[222-202]×38
=3.14×[484-400]×38
=3.14×84×38
=263.76×38
=10022.88(元)
答:购买这些草皮需10022.88元。
【点睛】掌握环形的面积计算公式以及单价、总价、数量之间的关系是解答题目的关键。
9.6.28厘米;0.86平方厘米
【分析】观察图形可知,涂色部分的周长等于直径是2厘米圆的周长,涂色部分的面积=正方形的面积-直径是2厘米圆的面积,根据圆的周长公式:C=πd,圆的面积公式:S=πr2,正方形的面积公式:S=a2,据此代入数值进行计算即可。
【详解】3.14×2=6.28(厘米)
2×2-3.14×(2÷2)2
=4-3.14×1
=4-3.14
=0.86(平方厘米)
答:涂色部分图形的周长是6.28厘米,涂色部分的面积是0.86平方厘米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
10.78.5厘米
【分析】看图,长方形的宽和圆的半径相等,同时面积也相等,所以长方形是圆的近似长方形,它的长是圆周长的一半。根据圆的周长公式,先求出圆周长,再除以2,求出长方形的长。用圆的周长除以4,求出阴影部分的弧长。最后,利用加法将组成阴影部分的各边(弧)相加,求出它的周长。
【详解】2×3.14×10=62.8(厘米)
62.8÷2=31.4(厘米)
62.8÷4=15.7(厘米)
15.7+31.4+10+(31.4-10)
=15.7+31.4+31.4
=78.5(厘米)
所以,阴影部分的周长是78.5厘米。
【点睛】此题主要考查长方形的面积公式、圆的面积公式、圆的周长公式的灵活运用,关键是熟记公式。
11.72平方厘米
【分析】根据题意,在圆内画一个最大的正方形,用正方形的一条对角线把这个正方形分成两个完全一样的三角形,三角形的底等于圆的直径,三角形的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2,就是这个正方形的面积。
【详解】圆的直径:6×2=12(厘米)
三角形的面积:
12×6÷2
=72÷2
=36(平方厘米)
正方形的面积:
36×2=72(平方厘米)
答:这个正方形的面积是72平方厘米。
【点睛】掌握圆内最大正方形的面积求法,把正方形的面积转移到两个三角形的面积上,找出三角形的底、高与圆的半径的关系,然后运用三角形的面积公式求解。
12.127.96厘米
【分析】如图,一圈长度=一个圆的周长+直径×6,一圈长度×2=绳子长度,据此列式解答。
【详解】3.14×7+7×6
=21.98+42
=63.98(厘米)
63.98×2=127.96(厘米)
答:这根绳子长127.96厘米。
【点睛】关键是看懂图示,掌握圆的周长公式,圆的周长:C=πd。
13.157平方米
【分析】根据题意,圆的周长的一半是31.4米,根据圆的周长公式:C=,则圆的周长的一半则为,代入即可求出圆的半径,再利用圆的面积公式:S=,代入数据后,再除以2,即可求出鸡舍的占地面积。
【详解】31.4÷3.14=10(米)
3.14×102÷2
=3.14×100÷2
=157(平方米)
答:这个鸡舍的占地面积是157平方米。
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式解决实际的问题。
14.(1)见详解
(2)21.14平方厘米
【分析】(1)通过观察图形,这个圆的直径是2厘米,根据圆的周长公式:,把数据代入公式求出这个圆的周长,据此在图中标出B点位置即可。
(2)根据题意可知,如果这个圆从点A滚动到点C,圆在整个滚动过程中所覆盖的面积=长为14-5=9(厘米)、宽为6-4=2(厘米)的长方形面积+一个圆的面积,然后再根据长方形的面积公式S=ab,圆的面积公式,把数据代入公式解答。
【详解】(1)3.14×(6-4)
=3.14×2
=6.28(厘米)
6.28+5=11.28(厘米)
作图如下:
(2)(14-5)×(6-4)+3.14×[(6-4)÷2]2
=9×2+3.14×[2÷2]2
=18+3.14×1
=18+3.14
=21.14(平方厘米)
答:所覆盖的面积是21.14平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
15.这只羊不能吃到全部的青草,具体见详解。
【分析】先画示意图,以木桩所在的地方为圆心,6米为圆心画圆,看圆是否覆盖整个长方形草地即可。也可以根据圆的面积公式求出羊所能吃到的面积,与长方形的面积比较即可。
【详解】如图所示,O点为木桩所在点,则羊的活动范围是以O为圆心,6米为半径的圆,即图中的蓝色区域。因为O点是草地的中央,那么OA的距离=15÷2=7.5(米),而6米<7.5米,所以羊不能吃到全部的青草。
或者:圆的面积=3.14×6×6=113.04(平方米),长方形的面积=20×15=300(平方米),113.04<300,所以这只羊不能吃到全部的青草。
答:这只羊不能吃到全部的青草。
【点睛】熟练掌握圆的面积公式与长方形的面积是解题的关键。
16.62.8米
【分析】相遇时间=相遇路程÷速度和,再根据猫每分钟比老鼠多走12.56米,乘相遇时间,求出当猫和老鼠第一次相遇时,猫比老鼠多走了多少米即可。
【详解】
(分钟)
(21.98-9.41)×5
=12.56×5
=62.8(米)
答:猫和老鼠第一次相遇时,猫比老鼠多走了62.8米。
【点睛】本题考查相遇问题、圆的周长,解答本题的关键是掌握相遇问题中的数量关系。
17.见详解
A到B转了1圈,B到C转了0.5圈,C到D转了1圈
【分析】小圆盘从A点转到B点,转动的长度是长方形的长边减去两个半径,也就是减去一条直径,用转动的长度除以圆的周长算出小圆圈转了几圈;从B点转到C点,转动的长度是长方形的宽边减去圆的直径,用转动的长度除以圆的周长算出小圆圈转了几圈;小圆盘从C点转到D点,转动的长度是长方形的长边减去一条直径,用转动的长度除以圆的周长算出小圆圈转了几圈,据此画图即可。
【详解】从A点转到B点转了:
(8.28-1×2)÷(2×3.14)
=(8.28-2)÷6.28
=6.28÷6.28
=1(圈)
转动了1整圈,娃娃脸的B位置同A位置一样;
从B点转到C点转了:
(5.14-1×2)÷(2×3.14)
=(5.14-2)÷6.28
=3.14÷6.28
=0.5(圈)
转动了半圈,娃娃脸的C位置跟B位置相反,眼睛朝下,嘴巴朝上;
从C点转到D点:
(8.28-1×2)÷(2×3.14)
=(8.28-2)÷6.28
=6.28÷6.28
=1(圈)
转动了1整圈,娃娃脸的D位置同C位置一样;
【点睛】本题主要考查圆的周长公式的灵活应用以及图形的旋转问题。
18.43.96平方米
【分析】根据圆环的面积公式求出整个环形的面积,阴影部分的面积是整个环形面积的一半,据此解答。
【详解】3.14×[(6+2)2-62]÷2
=3.14×[64-36]÷2
=3.14×28÷2
=87.92÷2
=43.96(平方米)
答:小路的面积是43.96平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第5单元圆应用题专项突破-数学六年级上册人教版
一、解答题
1.在探索圆的面积计算公式时,把圆平均分成32等份,将每份剪下后进行拼接,得到一个近似的长方形。图中圆的面积是多少平方厘米?
2.如图,这是体育馆运动场的设计图,这个运动场的周长是多少米?面积是多少平方米?
3.人民广场要修建一个圆形花坛,周长是18.84米,花坛面积是多少平方米?若在花坛的周围修一条宽1米的小路,小路的占地面积是多少平方米?
4.在下面的长方形内画一个最大的圆。
①求出这个圆的周长和面积。
②画出这个圆的互相垂直的两条对称轴。
5.一辆自行车车轮的外直径为72cm,王帆骑这辆自行车通过一座长2260.8m的大桥,如果期间车轮平均每分钟转100圈,那么他通过这座大桥需要几分钟?
6.一根长18.84米的绳子正好可以绕一棵树的树干10圈。树干横截面的直径大约是多少米?
7.公园里有一棵大树,同学们用一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,求树干的直径是多少?
8.一个圆形水池,它的半径20米,现要在水池周围种植草皮,草皮是宽为2米的环形,如果每平方米草皮38元,购买这些草皮需多少元?
9.下边涂色部分图形的周长是多少厘米?涂色部分的面积是多少平方厘米?
10.如图,圆的面积与长方形的面积正好相等。已知圆的半径为10厘米,求图中阴影部分的周长。
11.一个圆的半径是6厘米,在这个圆内画一个最大的正方形。这个正方形的面积是多少平方厘米?
12.如图,六罐啤酒用一根绳子捆了2圈,不计打结长度,这根绳子长多少厘米?
13.王爷爷靠墙用篱笆围了一个半圆形的鸡舍(如下图),篱笆的长是31.4米,这个鸡舍的占地面积是多少平方米?
14.如图,圆从点A开始,沿着直尺向右滚动一周后到达点B。
(1)请在直尺上标出点B的大概位置(在直尺上描上点,并标注上字母B)。
(2)如果这个圆从点A滚动到点C,请计算出滚动后(含起始状态)所覆盖的面积。(取3.14)
15.用6米长的绳子把一只羊拴在了一块长20米、宽15米的长方形草地中央的木桩上。请问:这只羊能吃到全部的青草吗?请说明理由。(提示:可以先画出示意图进行分析)
16.猫和老鼠在一个直径是50米的圆周上的同一地点向相反方向运动,猫每分钟走21.98米,老鼠每分钟走9.42米。当猫和老鼠第一次相遇时,猫比老鼠多走了多少米?
17.如下图所示,半径为1厘米的小圆盘(娃娃脸)沿着长方形内壁,从A点出发不停滚动(无滑动),最后到原来的位置。小圆盘在B、C、D位置是怎样的,请你计算一下并画出示意图。
18.如图所示:沿半圆形草坪铺一条2米宽的小路,小路的面积是多少平方米?
参考答案:
1.50.24平方厘米
【分析】近似长方形的长是圆周长的一半,那么将12.56厘米乘2,可以求出圆的周长,再将圆的周长除以2再除以圆周率3.14,求出圆的半径。最终,根据S=πr2,代入数据求出这个圆的面积即可。
【详解】12.56×2÷2÷3.14
=12.56÷3.14
=4(厘米)
3.14×42
=3.14×16
=50.24(平方厘米)
答:图中圆的面积是50.24平方厘米。
【点睛】本题考查了圆的周长和面积,解题关键是熟记公式。
2.453.76米;13518.96平方米
【分析】运动场是由两个半圆和一个长方形组成,运动场的周长=一个圆的周长+长方形的两条长,运动场的面积=一个圆的面积+一个长方形的面积。已知圆的半径,可根据求出圆的周长;根据求出圆的面积。已知长方形的长与宽,可根据“长方形的面积=长×宽”求出长方形的面积。
【详解】2×3.14×42+95×2
=6.28×42+190
=263.76+190
=453.76(米)
3.14×+95×(42×2)
=3.14×1764+95×84
=5538.96+7980
=13518.96(平方米)
答:这个运动场的周长是453.76米,面积是13518.96平方米。
【点睛】解决此题的关键是理解运动场的周长包含哪些边的长度,运动场的面积是哪些图形的面积和。
3.28.26平方米;21.98平方米
【分析】根据圆的周长公式C=2πr可知,圆的半径r=C÷π÷2,求出圆形花坛的半径;然后根据圆的面积公式S=πr2,求出花坛的面积;
若在花坛的周围修一条宽1米的小路,求小路的占地面积就是求圆环的面积;内圆的半径r等于圆形花坛的半径,外圆的半径R等于花坛的半径加上1米;然后根据圆环的面积公式S环=π(R2-r2),代入数据计算即可。
【详解】圆形花坛的半径:
18.84÷3.14÷2
=6÷2
=3(米)
花坛的面积:
3.14×32
=3.14×9
=28.26(平方米)
外圆半径:3+1=4(米)
小路的面积:
3.14×(42-32)
=3.14×(16-9)
=3.14×7
=21.98(平方米)
答:花坛面积是28.26平方米,小路的占地面积是21.98平方米。
【点睛】本题考查圆的周长、圆的面积、圆环的面积公式的灵活运用,求出内圆和外圆的半径是解题的关键。
4.图形见详解
①12.56厘米;12.56平方厘米;
②见详解
【分析】以长方形的宽为直径的圆是长方形内面积最大的圆,再根据“”和“”求出这个圆的周长和面积,将图形沿着一条直线对折,如果直线两侧的部分能够完全重合,折痕所在的直线叫做它的对称轴,每条直径所在的直线就是圆的对称轴,最后用虚线画出两条互相垂直的对称轴,据此解答。
【详解】①周长:3.14×4=12.56(厘米)
面积:3.14×(4÷2)2
=3.14×4
=12.56(平方厘米)
答:这个圆的周长是12.56厘米,面积是12.56平方厘米。
②分析可知:
【点睛】掌握圆的周长和面积计算公式,并根据对称轴的定义画出符合条件的对称轴是解答题目的关键。
5.10分钟
【分析】根据圆的周长=πd,求出车轮转一圈行进的距离,车轮周长×每分钟转动圈数=每分钟行驶距离,统一单位,根据时间=路程÷速度,列式解答即可。
【详解】3.14×72×100=22608(厘米)=226.08(米)
2260.8÷226.08=10(分钟)
答:他通过这座大桥需要10分钟。
【点睛】关键是掌握圆的周长公式,理解速度、时间、路程之间的关系。
6.0.6米
【分析】先用除法表示出树干一圈的长度,再根据“”求出树干横截面的直径,据此解答。
【详解】18.84÷10÷3.14
=1.884÷3.14
=0.6(米)
答:树干横截面的直径大约是0.6米。
【点睛】掌握圆的周长计算公式是解答题目的关键。
7.1米
【分析】已知一根20米长的绳子围绕这棵树绕了6圈,还剩下1.16米,先用20米减去1.16米,再除以6即可求出一圈的长度,然后根据圆的周长公式求解出树干的直径即可。
【详解】(20-1.16)÷6
=18.84÷6
=3.14(米)
3.14÷3.14=1(米)
答:树干的直径是1米。
【点睛】本题考查了圆周长公式的灵活应用。
8.10022.88元
【分析】由题意可知,小圆半径为20米,环宽为2米,则大圆半径为(20+2)米,利用“”求出环形的面积,最后根据“总价=单价×数量”求出购买草皮需要花费的总钱数,据此解答。
【详解】3.14×[(20+2)2-202]×38
=3.14×[222-202]×38
=3.14×[484-400]×38
=3.14×84×38
=263.76×38
=10022.88(元)
答:购买这些草皮需10022.88元。
【点睛】掌握环形的面积计算公式以及单价、总价、数量之间的关系是解答题目的关键。
9.6.28厘米;0.86平方厘米
【分析】观察图形可知,涂色部分的周长等于直径是2厘米圆的周长,涂色部分的面积=正方形的面积-直径是2厘米圆的面积,根据圆的周长公式:C=πd,圆的面积公式:S=πr2,正方形的面积公式:S=a2,据此代入数值进行计算即可。
【详解】3.14×2=6.28(厘米)
2×2-3.14×(2÷2)2
=4-3.14×1
=4-3.14
=0.86(平方厘米)
答:涂色部分图形的周长是6.28厘米,涂色部分的面积是0.86平方厘米。
【点睛】本题考查圆的周长和面积,熟记公式是解题的关键。
10.78.5厘米
【分析】看图,长方形的宽和圆的半径相等,同时面积也相等,所以长方形是圆的近似长方形,它的长是圆周长的一半。根据圆的周长公式,先求出圆周长,再除以2,求出长方形的长。用圆的周长除以4,求出阴影部分的弧长。最后,利用加法将组成阴影部分的各边(弧)相加,求出它的周长。
【详解】2×3.14×10=62.8(厘米)
62.8÷2=31.4(厘米)
62.8÷4=15.7(厘米)
15.7+31.4+10+(31.4-10)
=15.7+31.4+31.4
=78.5(厘米)
所以,阴影部分的周长是78.5厘米。
【点睛】此题主要考查长方形的面积公式、圆的面积公式、圆的周长公式的灵活运用,关键是熟记公式。
11.72平方厘米
【分析】根据题意,在圆内画一个最大的正方形,用正方形的一条对角线把这个正方形分成两个完全一样的三角形,三角形的底等于圆的直径,三角形的高等于圆的半径,根据三角形的面积=底×高÷2,即可求出一个三角形的面积,再乘2,就是这个正方形的面积。
【详解】圆的直径:6×2=12(厘米)
三角形的面积:
12×6÷2
=72÷2
=36(平方厘米)
正方形的面积:
36×2=72(平方厘米)
答:这个正方形的面积是72平方厘米。
【点睛】掌握圆内最大正方形的面积求法,把正方形的面积转移到两个三角形的面积上,找出三角形的底、高与圆的半径的关系,然后运用三角形的面积公式求解。
12.127.96厘米
【分析】如图,一圈长度=一个圆的周长+直径×6,一圈长度×2=绳子长度,据此列式解答。
【详解】3.14×7+7×6
=21.98+42
=63.98(厘米)
63.98×2=127.96(厘米)
答:这根绳子长127.96厘米。
【点睛】关键是看懂图示,掌握圆的周长公式,圆的周长:C=πd。
13.157平方米
【分析】根据题意,圆的周长的一半是31.4米,根据圆的周长公式:C=,则圆的周长的一半则为,代入即可求出圆的半径,再利用圆的面积公式:S=,代入数据后,再除以2,即可求出鸡舍的占地面积。
【详解】31.4÷3.14=10(米)
3.14×102÷2
=3.14×100÷2
=157(平方米)
答:这个鸡舍的占地面积是157平方米。
【点睛】此题的解题关键是灵活运用圆的周长和圆的面积公式解决实际的问题。
14.(1)见详解
(2)21.14平方厘米
【分析】(1)通过观察图形,这个圆的直径是2厘米,根据圆的周长公式:,把数据代入公式求出这个圆的周长,据此在图中标出B点位置即可。
(2)根据题意可知,如果这个圆从点A滚动到点C,圆在整个滚动过程中所覆盖的面积=长为14-5=9(厘米)、宽为6-4=2(厘米)的长方形面积+一个圆的面积,然后再根据长方形的面积公式S=ab,圆的面积公式,把数据代入公式解答。
【详解】(1)3.14×(6-4)
=3.14×2
=6.28(厘米)
6.28+5=11.28(厘米)
作图如下:
(2)(14-5)×(6-4)+3.14×[(6-4)÷2]2
=9×2+3.14×[2÷2]2
=18+3.14×1
=18+3.14
=21.14(平方厘米)
答:所覆盖的面积是21.14平方厘米。
【点睛】此题主要考查圆的周长公式、面积公式、长方形的面积公式的灵活运用,关键是熟记公式。
15.这只羊不能吃到全部的青草,具体见详解。
【分析】先画示意图,以木桩所在的地方为圆心,6米为圆心画圆,看圆是否覆盖整个长方形草地即可。也可以根据圆的面积公式求出羊所能吃到的面积,与长方形的面积比较即可。
【详解】如图所示,O点为木桩所在点,则羊的活动范围是以O为圆心,6米为半径的圆,即图中的蓝色区域。因为O点是草地的中央,那么OA的距离=15÷2=7.5(米),而6米<7.5米,所以羊不能吃到全部的青草。
或者:圆的面积=3.14×6×6=113.04(平方米),长方形的面积=20×15=300(平方米),113.04<300,所以这只羊不能吃到全部的青草。
答:这只羊不能吃到全部的青草。
【点睛】熟练掌握圆的面积公式与长方形的面积是解题的关键。
16.62.8米
【分析】相遇时间=相遇路程÷速度和,再根据猫每分钟比老鼠多走12.56米,乘相遇时间,求出当猫和老鼠第一次相遇时,猫比老鼠多走了多少米即可。
【详解】
(分钟)
(21.98-9.41)×5
=12.56×5
=62.8(米)
答:猫和老鼠第一次相遇时,猫比老鼠多走了62.8米。
【点睛】本题考查相遇问题、圆的周长,解答本题的关键是掌握相遇问题中的数量关系。
17.见详解
A到B转了1圈,B到C转了0.5圈,C到D转了1圈
【分析】小圆盘从A点转到B点,转动的长度是长方形的长边减去两个半径,也就是减去一条直径,用转动的长度除以圆的周长算出小圆圈转了几圈;从B点转到C点,转动的长度是长方形的宽边减去圆的直径,用转动的长度除以圆的周长算出小圆圈转了几圈;小圆盘从C点转到D点,转动的长度是长方形的长边减去一条直径,用转动的长度除以圆的周长算出小圆圈转了几圈,据此画图即可。
【详解】从A点转到B点转了:
(8.28-1×2)÷(2×3.14)
=(8.28-2)÷6.28
=6.28÷6.28
=1(圈)
转动了1整圈,娃娃脸的B位置同A位置一样;
从B点转到C点转了:
(5.14-1×2)÷(2×3.14)
=(5.14-2)÷6.28
=3.14÷6.28
=0.5(圈)
转动了半圈,娃娃脸的C位置跟B位置相反,眼睛朝下,嘴巴朝上;
从C点转到D点:
(8.28-1×2)÷(2×3.14)
=(8.28-2)÷6.28
=6.28÷6.28
=1(圈)
转动了1整圈,娃娃脸的D位置同C位置一样;
【点睛】本题主要考查圆的周长公式的灵活应用以及图形的旋转问题。
18.43.96平方米
【分析】根据圆环的面积公式求出整个环形的面积,阴影部分的面积是整个环形面积的一半,据此解答。
【详解】3.14×[(6+2)2-62]÷2
=3.14×[64-36]÷2
=3.14×28÷2
=87.92÷2
=43.96(平方米)
答:小路的面积是43.96平方米。
【点睛】掌握环形的面积计算公式是解答题目的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
