2等边三角形(1
图片预览





文档简介
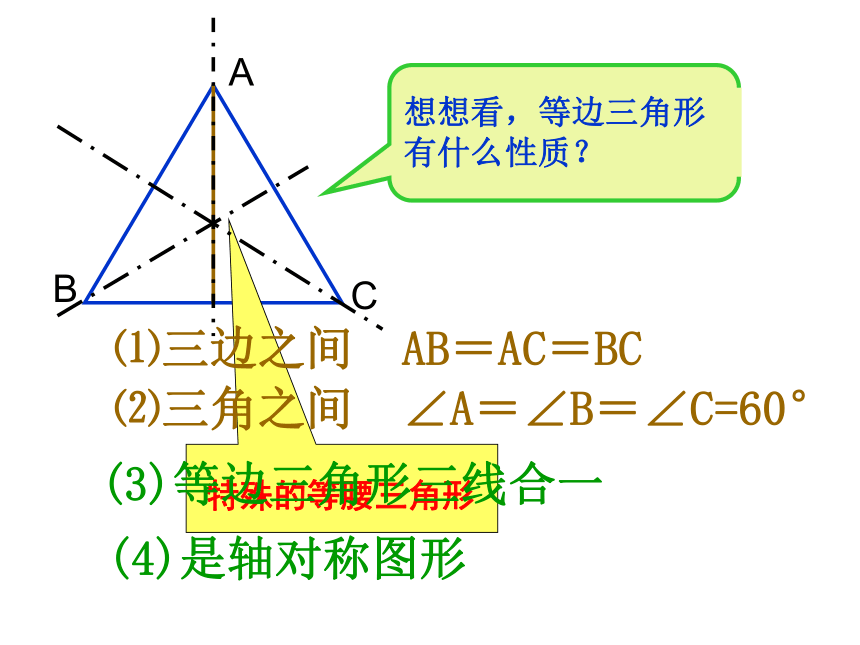
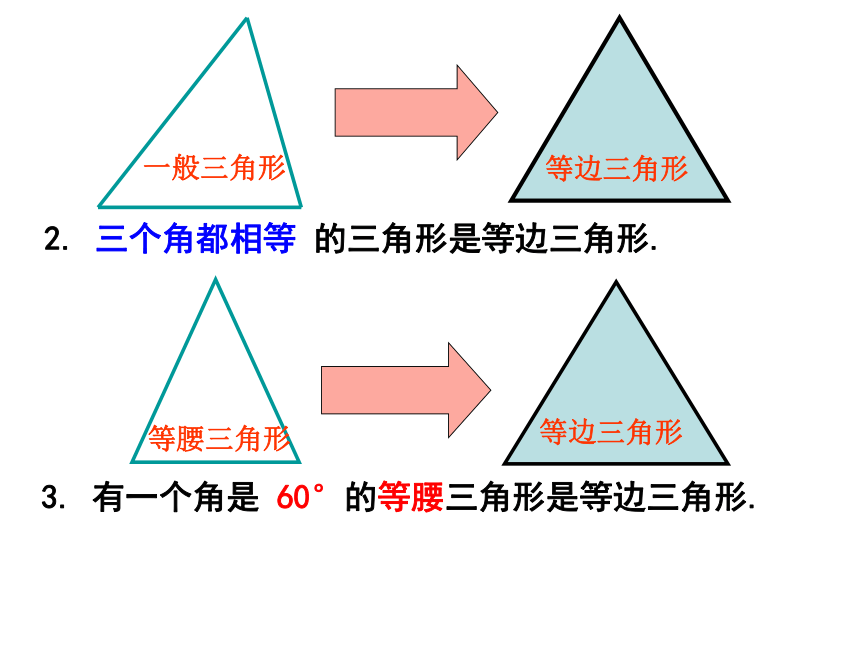
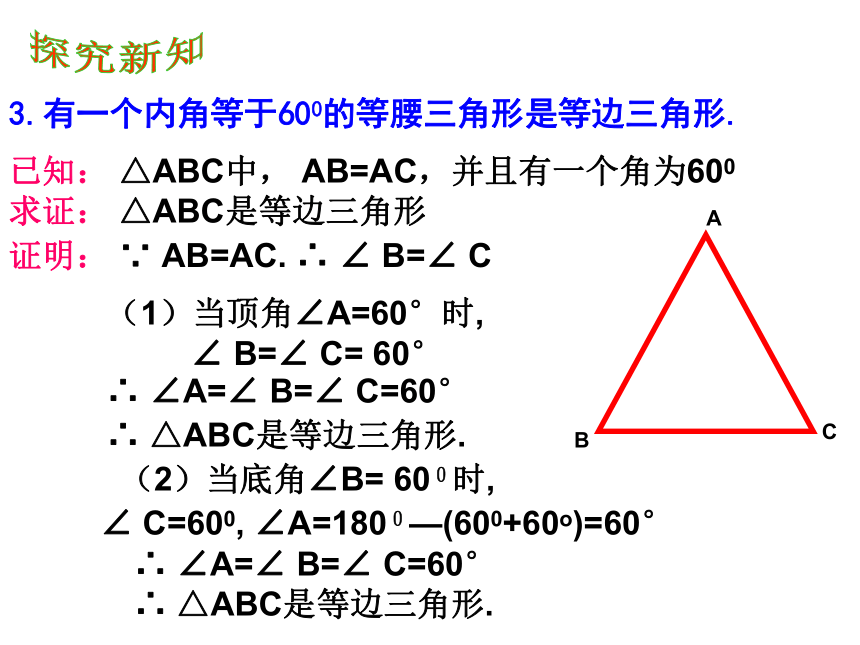
课件29张PPT。12.3.2等边三角形(1)什么是等边三角形?三条边都相等的三角形叫等边三角形,也叫正三角形。等腰三角形与等边三角形有什么关系?ABC⑴三边之间 AB=AC=BC⑵三角之间 ∠A=∠B=∠C=60°(3)等边三角形三线合一(4)是轴对称图形等边三角形的性质3.等边三角形各边上中线,高和所对角的平分线都三线合一.4.等边三角形是轴对称图形,有三条对称轴. 2. 等边三角形的三个内角都相等,且等于60 ° 归纳1. 等边三角形三边都相等思考题?一个三角形满足什么条件就是等边三角形?判定方法1:三边都相等的三角形是等边三角形定 义2. 三个角都相等 的三角形是等边三角形.3. 有一个角是 60°的等腰三角形是等边三角形.探究新知3.有一个内角等于600的等腰三角形是等边三角形.已知: △ABC中, AB=AC,并且有一个角为600
求证: △ABC是等边三角形证明: ∵ AB=AC. ∴ ∠ B=∠ C(1)当顶角∠A=60°时,
∠ B=∠ C= 60°∴ ∠A=∠ B=∠ C=60°
∴ △ABC是等边三角形.(2)当底角∠B= 600时,∠ C=600, ∠A=1800—(600+60o)=60°∴ ∠A=∠ B=∠ C=60°
∴ △ABC是等边三角形.等边三角形的判定方法:1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个角是600的等腰三角形是等边三角形.
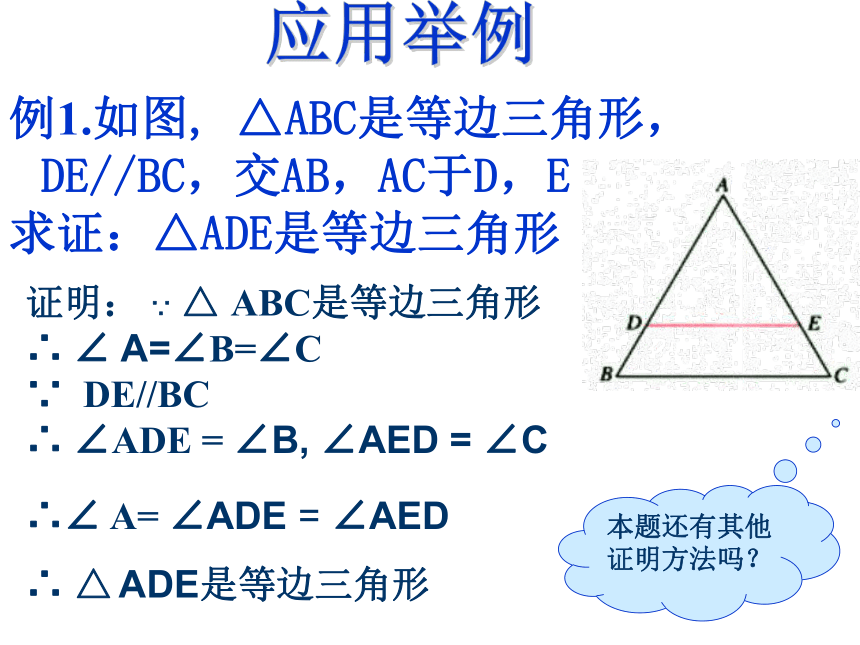
归纳应用举例例1.如图, △ABC是等边三角形,DE//BC,交AB,AC于D,E
求证:△ADE是等边三角形本题还有其他证明方法吗?证明: ∵ △ ABC是等边三角形
∴ ∠ A=∠B=∠C
∵ DE//BC
∴ ∠ADE = ∠B, ∠AED = ∠C
∴∠ A= ∠ADE = ∠AED
∴ △ ADE是等边三角形变式1:如图,在等边三角形ABC的边AB、AC
上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。变式2:等边三角形ABC,D、E分别是AB、AC上的中点,求证:2DE=BC例2.如图, △ABC为等边三角形,
∠ 1= ∠ 2= ∠ 3
(1)求∠EDF的度数.
(2)△DEF为等边三角形吗?为什么? 已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.
△ DEF是等边三角形吗?ADCFBE变式:探究:
等边三角形三条中线相交于一点,画出图形,找出图中所有的全等三角形。1. 如图,等边三角形ABC 中, AD是 BC上的高, ∠BDE = ∠CDF= 60 °,图中有哪些与BD相等的线段?∴与BD相等的线段有
CD,CF,BE,DE,
FD,AF,AE想一想想一想2.课外活动小组在一次测量活动中,测得
∠APB=60°AP=BP=200cm,他们
便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?B//有二条边相等1、等边对等角
2、三线合一
3、对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、两个角是600
3、等腰三角形
有一个角是600 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?图形种类类别说一说巩固练习
1.等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?A2.已知:如图,P、Q是△ABC的边BC上的两点,并且PB=PQ=QC=AP=AQ.
求∠BAC的大小.ABPQC////﹚3.如图,已知△ABC是等边三角形,D是AC的中点,EC⊥BC,且EC=BD。
求证:△ADE是等边三角形.==∟(1) 等边三角形的性质.
小结:1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.3.已知在等边△ABC中,如果P是△ABC所在平面上的一点,且△PAB、△PBC、△PCA都是等腰三角形,那么这样的点P的位置共有几个?试一一画出。 ?
?
?
ABC·P1小小探索家:作业作业本(2)
B本
课本习题(部分)解:(1)?AOB,?BOC,?COA彼此全等,
理由如下:因为AD,BE,CF是等边三角形ABC的角平分线,
所以它们所在的直线也就是等边三角形ABC的三条
对称轴,则?AOB与?AOC关于直线AD成轴对称,所以?AOB??AOC。
同理, ?AOB? ?BOC,也就是说?AOB,?BOC,?COA 彼此全等。 例2 如图,等边△ABC中,三条内角平分线AD,BE,CF相交于点O。(1)?AOB, ? BOC和?AOC有什么关系?例题分析CA解:(2)由?AOB ,?BOC,?AOC彼此全等,得?AOB=?BOC=?AOC(全等三角形的对应角相等),
OA=OB=OC(根据什么?) EFCBA DO??AOB+?BOC+?AOC=360°(2)求?AOB,?BOC,?AOC的度数,将?ABC绕点O旋转,问要旋转多少度,就能和原来的三角形重合(只要求说出一个旋转度数)???AOB=?BOC=?AOC= × 360°=120°由此可知,将ABC绕点O旋转120°,就能和原来的三角形重合。在等边△ABC所在的平面上找一点P,使△ PAB、 △ PBC、 △ PAC都是等腰三角形,你能找到这样的点P吗? 能找到多少个?这些点的位置有什么特点?思维发散已知,如图△ABC和△DCE都为等边三角形,AE交CD于点N,BD交AC于点M.
①试找出图中相等的线段相等的角.
②连结MN,图中还有等边三角形吗?ABCDEMN③∠APB=?考考你有二条边相等1、等边对等角
2、三线合一
3、对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、两个角是600
3、等腰三角形
有一个角是600 等边三角形与等腰三角形在定义,性质和判定的异同点图形种类类别再见
求证: △ABC是等边三角形证明: ∵ AB=AC. ∴ ∠ B=∠ C(1)当顶角∠A=60°时,
∠ B=∠ C= 60°∴ ∠A=∠ B=∠ C=60°
∴ △ABC是等边三角形.(2)当底角∠B= 600时,∠ C=600, ∠A=1800—(600+60o)=60°∴ ∠A=∠ B=∠ C=60°
∴ △ABC是等边三角形.等边三角形的判定方法:1.三边相等的三角形是等边三角形.
2.三个内角都相等的三角形是等边三角形.
3.有一个角是600的等腰三角形是等边三角形.
归纳应用举例例1.如图, △ABC是等边三角形,DE//BC,交AB,AC于D,E
求证:△ADE是等边三角形本题还有其他证明方法吗?证明: ∵ △ ABC是等边三角形
∴ ∠ A=∠B=∠C
∵ DE//BC
∴ ∠ADE = ∠B, ∠AED = ∠C
∴∠ A= ∠ADE = ∠AED
∴ △ ADE是等边三角形变式1:如图,在等边三角形ABC的边AB、AC
上分别截取AD=AE,△ADE是等边三
角形吗?试说明理由。变式2:等边三角形ABC,D、E分别是AB、AC上的中点,求证:2DE=BC例2.如图, △ABC为等边三角形,
∠ 1= ∠ 2= ∠ 3
(1)求∠EDF的度数.
(2)△DEF为等边三角形吗?为什么? 已知△ABC是等边三角形,D,E,F分别是各边上的一点,且AD=BE=CF.
△ DEF是等边三角形吗?ADCFBE变式:探究:
等边三角形三条中线相交于一点,画出图形,找出图中所有的全等三角形。1. 如图,等边三角形ABC 中, AD是 BC上的高, ∠BDE = ∠CDF= 60 °,图中有哪些与BD相等的线段?∴与BD相等的线段有
CD,CF,BE,DE,
FD,AF,AE想一想想一想2.课外活动小组在一次测量活动中,测得
∠APB=60°AP=BP=200cm,他们
便得到了一个结论:池塘最长处不小
于200cm.他们的结论对吗?B//有二条边相等1、等边对等角
2、三线合一
3、对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、两个角是600
3、等腰三角形
有一个角是600 等边三角形是一种特殊的等腰三角形,你能述说等边三角形与等腰三角形在定义,性质和判定的异同吗?图形种类类别说一说巩固练习
1.等边三角形中,高、中线、角平分线共有( )
(A)3条(B)6条(C)9条(D)7条
?A2.已知:如图,P、Q是△ABC的边BC上的两点,并且PB=PQ=QC=AP=AQ.
求∠BAC的大小.ABPQC////﹚3.如图,已知△ABC是等边三角形,D是AC的中点,EC⊥BC,且EC=BD。
求证:△ADE是等边三角形.==∟(1) 等边三角形的性质.
小结:1.等边三角形的内角都相等,且等于60 °
2.等边三角形是轴对称图形,有三条对称轴.
3.等边三角形各边上中线,高和所对角的平 分线都三线合一.(2) 等边三角形的判定:1.三边相等的三角形是等边三角形.
2.三个内角都等于60 °的三角形是等边三角形.
3.有一个内角等于60 °的等腰三角形是等边三角形.3.已知在等边△ABC中,如果P是△ABC所在平面上的一点,且△PAB、△PBC、△PCA都是等腰三角形,那么这样的点P的位置共有几个?试一一画出。 ?
?
?
ABC·P1小小探索家:作业作业本(2)
B本
课本习题(部分)解:(1)?AOB,?BOC,?COA彼此全等,
理由如下:因为AD,BE,CF是等边三角形ABC的角平分线,
所以它们所在的直线也就是等边三角形ABC的三条
对称轴,则?AOB与?AOC关于直线AD成轴对称,所以?AOB??AOC。
同理, ?AOB? ?BOC,也就是说?AOB,?BOC,?COA 彼此全等。 例2 如图,等边△ABC中,三条内角平分线AD,BE,CF相交于点O。(1)?AOB, ? BOC和?AOC有什么关系?例题分析CA解:(2)由?AOB ,?BOC,?AOC彼此全等,得?AOB=?BOC=?AOC(全等三角形的对应角相等),
OA=OB=OC(根据什么?) EFCBA DO??AOB+?BOC+?AOC=360°(2)求?AOB,?BOC,?AOC的度数,将?ABC绕点O旋转,问要旋转多少度,就能和原来的三角形重合(只要求说出一个旋转度数)???AOB=?BOC=?AOC= × 360°=120°由此可知,将ABC绕点O旋转120°,就能和原来的三角形重合。在等边△ABC所在的平面上找一点P,使△ PAB、 △ PBC、 △ PAC都是等腰三角形,你能找到这样的点P吗? 能找到多少个?这些点的位置有什么特点?思维发散已知,如图△ABC和△DCE都为等边三角形,AE交CD于点N,BD交AC于点M.
①试找出图中相等的线段相等的角.
②连结MN,图中还有等边三角形吗?ABCDEMN③∠APB=?考考你有二条边相等1、等边对等角
2、三线合一
3、对称轴一条1、等边对等角
2、三线合一
3、对称轴三条有三条边相等1、定义
2、等角对等边1、定义
2、两个角是600
3、等腰三角形
有一个角是600 等边三角形与等腰三角形在定义,性质和判定的异同点图形种类类别再见
