圆的切线(复习课)

课件13张PPT。圆的切线（习题课）
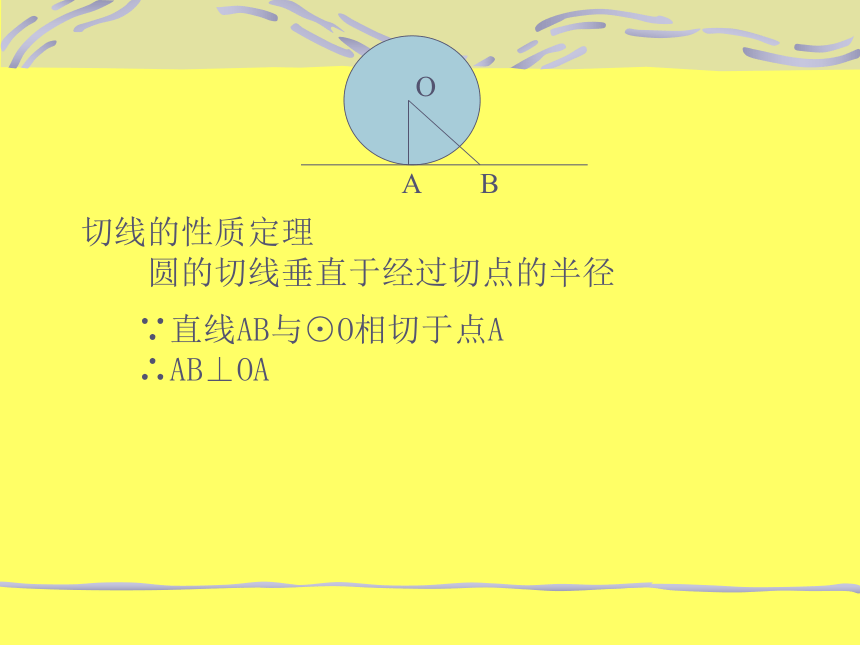
OAB 切线的性质定理
圆的切线垂直于经过切点的半径∵直线AB与⊙O相切于点A
∴AB⊥OA
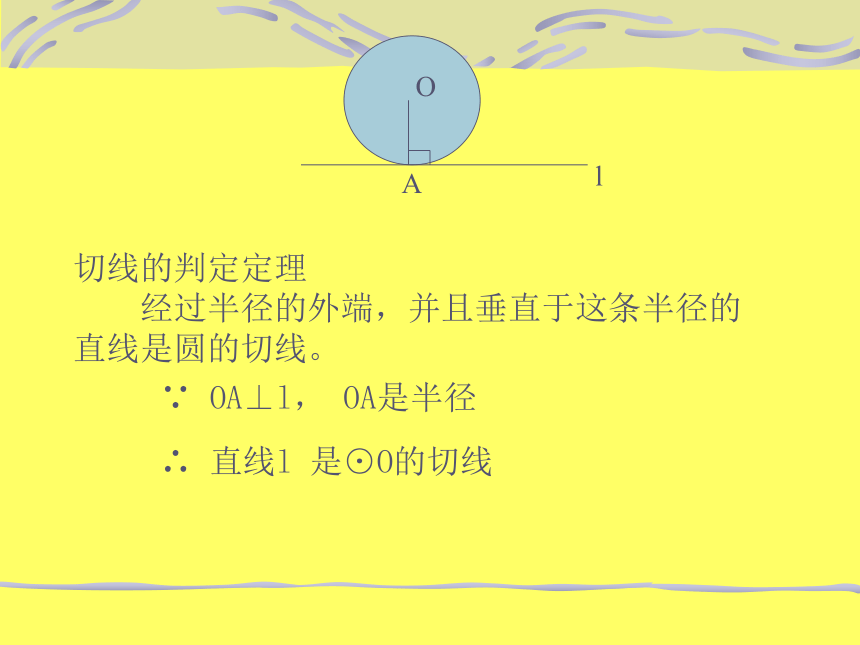
OAl切线的判定定理
经过半径的外端，并且垂直于这条半径的
直线是圆的切线。∵ OA⊥l， OA是半径∴ 直线l 是⊙O的切线
OAl已知：如图，OA是⊙O的半径，OA⊥直线l，垂足为A
求证：直线l是⊙O的切线证明：∵半径OA⊥直线l ，垂足为A∴点O到l的距离d=OA∴直线l 是⊙O的切线
OAB 例1 如图，已知⊙O的半径为R，直线AB经过
⊙O上的点A,并且AB=R,∠OBA=45°
求证：直线AB是⊙O的切线

∵ OA是半径
∴直线AB是⊙O的切线
证明：连结OA
∵ OA=AB=R
∴∠O=∠OBA=45 °
∵∠O+∠OBA+∠OAB=180°
∴∠OAB=90°
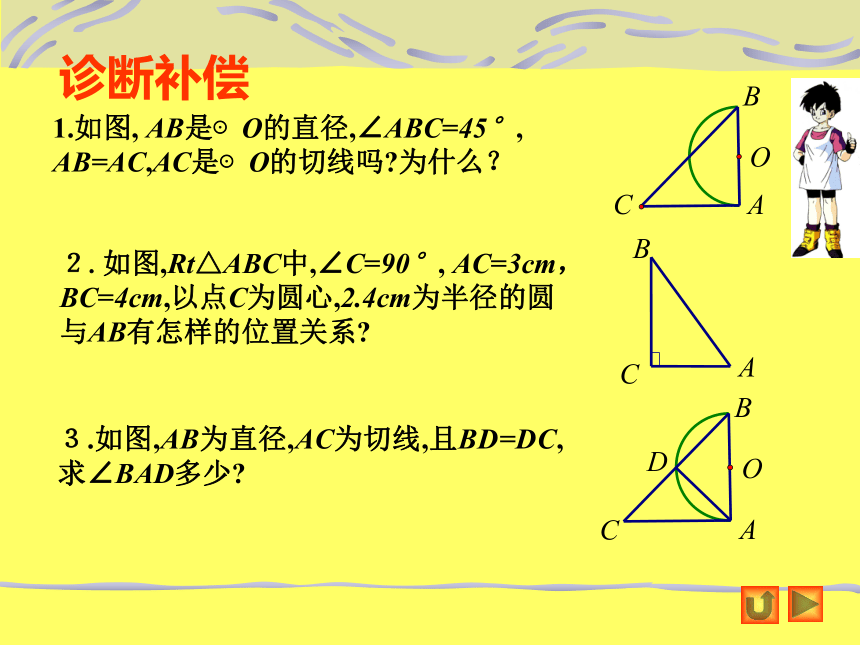
诊断补偿1.如图, AB是⊙O的直径,∠ABC=45°,
AB=AC,AC是⊙O的切线吗?为什么？ ３.如图,AB为直径,AC为切线,且BD=DC,求∠BAD多少? ２.如图,Rt△ABC中,∠C=90°, AC=3cm，BC=4cm,以点C为圆心,2.4cm为半径的圆与AB有怎样的位置关系?B范例提炼如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点切线互相垂直，垂足为D. 求证:AC平分∠DAB连结OC
∵CD是⊙O的切线∴OC⊥CD
又∵CD⊥AD∴OC∥AD ∴∠1=∠3
又∵OA=OC
∴∠2=∠3 ∴ ∠1=∠2
即AC平分∠DAB 证明:小提示：连结圆心与切点是作辅助线常用的方法之一. 3 2 1 O D 如图,AB为⊙O的直径, C为⊙O上一点,AD⊥CD,AC平分∠DAB.
求证: CD是⊙O的切线变式1变式2如图,AB为⊙O的直径, AC平分∠DAB ,CD是⊙O的切线.
求证: AD⊥CD3 2 1 BO A C D变式导练已知:如图, AB是⊙O的直径,⊙O过BE的中点C,CD⊥AE.
求证:DC是⊙O的切线.证明:连结AC,OC
∵AB为⊙O的直径∴AC⊥BE
又∵BC=EC∴AE=AB ∴∠1=∠2
又∵OA=OC∴∠2=∠3∴∠1=∠3
∴AE∥OC
∵CD⊥AE
∴DC⊥OC
∴DC是⊙O的切线.两图比较E能力提高已知:AB是⊙O的直径, ⊙O过AC的中点,DE⊥BC,垂足为E.
⑴这些条件你能推出哪些正确的结论?(所连辅助线不要出现在结论中.不写推理过程,写出3个结论即可)⑵当∠ABC为直角时,其他条件不变,除上述结论外,你还能推出哪些正确的结论?(要求将图画出,写出4个结论取即可)EDCOBA交流评价本节课你的收获是什么?切线的性质圆的切线垂直于过切点的直径切线的判定经过直径的一端并且垂直于直径的直线是圆的切线.直线L与圆相切d = r一种常用的辅助线连结圆心与切点是作辅助线常用的方法之一. 再见