24.2.1点和圆的位置关系(1)
文档属性
| 名称 | 24.2.1点和圆的位置关系(1) |
|
|
| 格式 | rar | ||
| 文件大小 | 188.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-10-28 00:00:00 | ||
图片预览



文档简介
(共17张PPT)
点和圆的位置关系
探究:1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
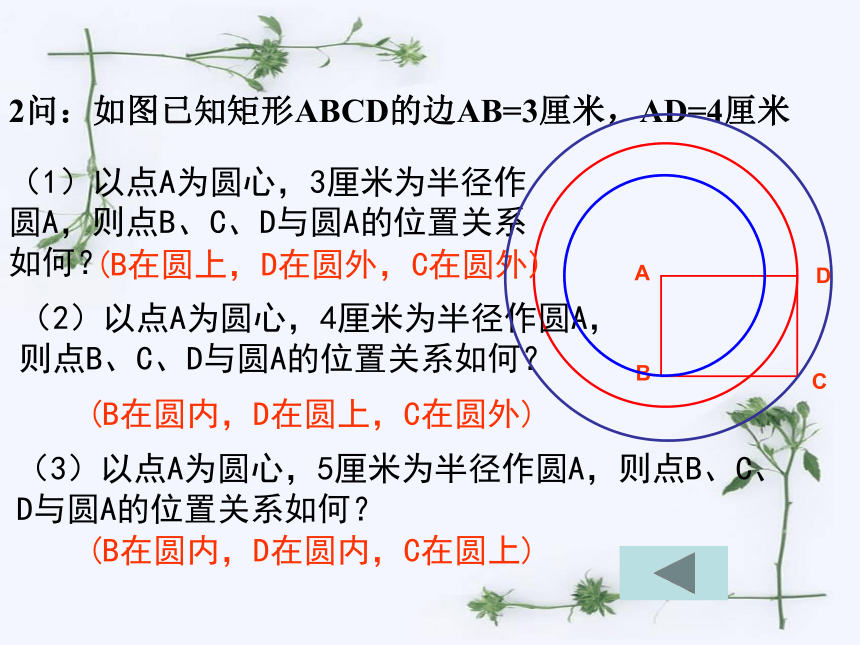
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
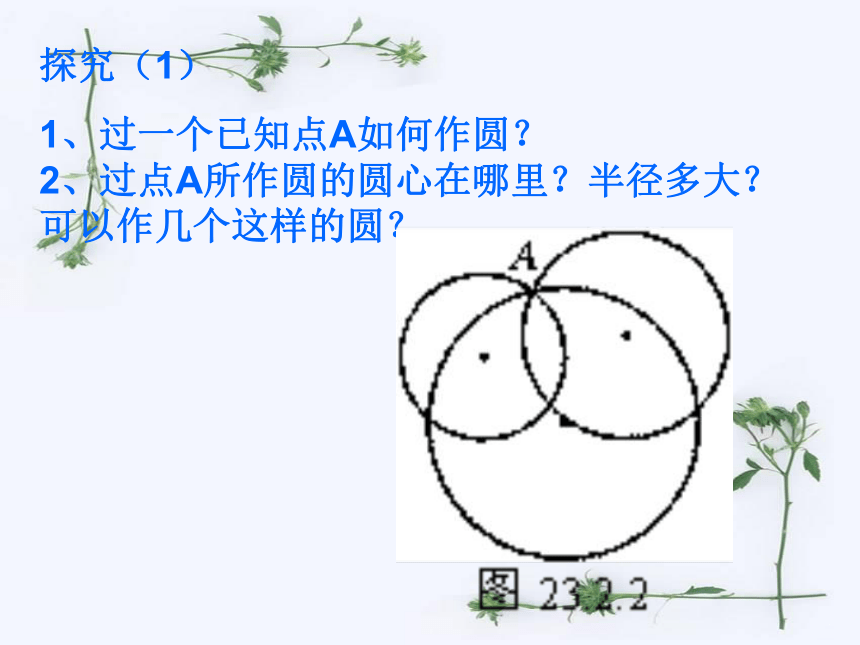
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
探究(1)
1、过一个已知点A如何作圆? 2、过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?
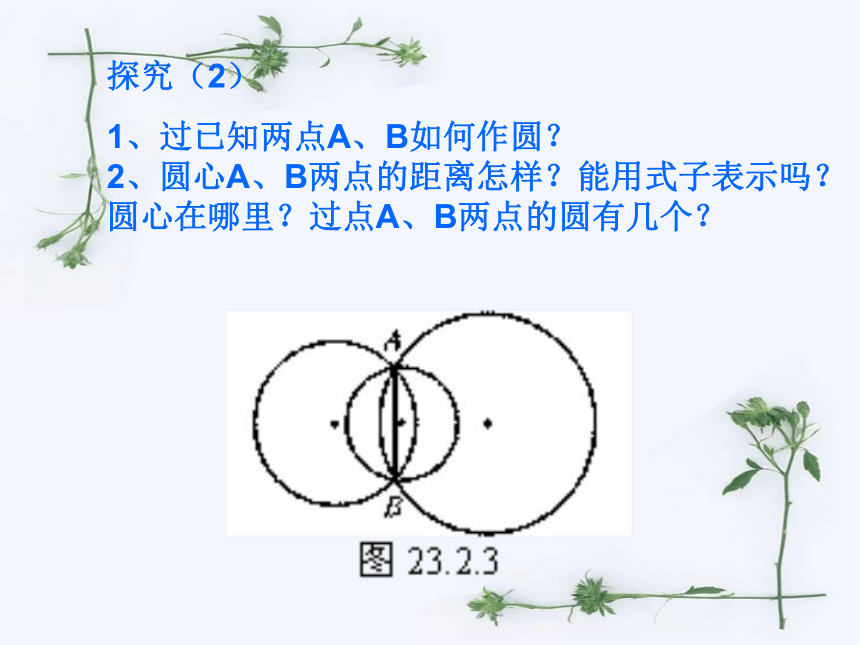
探究(2)
1、过已知两点A、B如何作圆? 2、圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个?
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
定理:过不在同一直线上的三点确定一个圆。
2、过在同一直线上的三点A、B、C可以作几个圆?
不能作出。
B
A
C
O
阅读92页,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆(circumcircle).三角形外接圆的圆心叫做这个三角形的外心(circumcenter).这个三角形叫做这个圆的内接三角形.三角形的外心就是三角形三条边的垂直平分线的交点.
B
A
C
O
●
想一想:
锐角三角形、直角三角 形、钝角三角形的外心各在哪里?
B
●
C
A
B
A
C
·
练习
例1、判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
×
√
×
×
练习
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考
1、过三角形的三个顶点是否都可以作圆?为什么?
2、一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
3、三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。
应用
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
作业
练 习
1. 任意画一个三角形,然后再画这个三角形的外接圆.
2. 随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆经过这四点?请举例说明.
再 见!
点和圆的位置关系
探究:1、请你在练习本上画一个圆,然后任意作一些点,观察这些点和圆的位置关系。
2、量一量这些点到圆心的距离。你发现了什么?
设⊙O的半径为r,点到圆心的距离为d。则
点和圆的位置关系
点在圆内
d﹤r
点在圆上
点在圆外
d=r
d>r
练习:已知圆的半径等于5厘米,点到圆心的距离是:
1、8厘米 2、4厘米 3、5厘米。
请你分别说出点与圆的位置关系。
●
●
●
2问:如图已知矩形ABCD的边AB=3厘米,AD=4厘米
A
D
C
B
(1)以点A为圆心,3厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆上,D在圆外,C在圆外)
(2)以点A为圆心,4厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆上,C在圆外)
(3)以点A为圆心,5厘米为半径作圆A,则点B、C、D与圆A的位置关系如何?
(B在圆内,D在圆内,C在圆上)
探究(1)
1、过一个已知点A如何作圆? 2、过点A所作圆的圆心在哪里?半径多大?可以作几个这样的圆?
探究(2)
1、过已知两点A、B如何作圆? 2、圆心A、B两点的距离怎样?能用式子表示吗?圆心在哪里?过点A、B两点的圆有几个?
探究(3)1、过同一平面内三个点的情况会怎样呢?
1、不在同一直线上的三点A、B、C。
定理:过不在同一直线上的三点确定一个圆。
2、过在同一直线上的三点A、B、C可以作几个圆?
不能作出。
B
A
C
O
阅读92页,完成以下填空:
如图:⊙O是△ ABC的 圆, △ ABC
是⊙O的 三角形,O是△ ABC的 心,它是 的交点,到
三角形 的距离相等。
外接
内接
外
三角形三边垂直平分线
三个顶点
●
经过三角形三个顶点可以画一个圆,并且只能画一个.经过三角形三个顶点的圆叫做三角形的外接圆(circumcircle).三角形外接圆的圆心叫做这个三角形的外心(circumcenter).这个三角形叫做这个圆的内接三角形.三角形的外心就是三角形三条边的垂直平分线的交点.
B
A
C
O
●
想一想:
锐角三角形、直角三角 形、钝角三角形的外心各在哪里?
B
●
C
A
B
A
C
·
练习
例1、判断:
1、经过三点一定可以作圆。( )
2、三角形的外心就是这个三角形两边垂直平分线的交点。( )
3、三角形的外心到三边的距离相等。( )
4、经过不在一直线上的四点能作一个圆。( )
×
√
×
×
练习
例2、填空:
1、已知⊙O的半径为4,OP=3.4,则P在⊙O的 ( )。
2、已知 点P在 ⊙O的外部,OP=5,那么⊙O的半径r满足( )
3、 已知⊙O的半径为5,M为ON的中点,当OM=3时,N点与⊙O的位置关系是N在⊙O的( )
内部
0﹤r ﹤5
外部
一位考古学家在马王堆汉墓挖掘时,发现一圆形瓷器碎片,你能帮助这位考古学家画出这个碎片所在的整圆,以便于进行深入的研究吗?
思考
1、过三角形的三个顶点是否都可以作圆?为什么?
2、一个三角形的外接圆有几个?一个圆的内接三角形有几个?为什么?
3、三角形的外心有什么性质?它一定在三角形的内部吗?画图说明。
应用
某一个城市在一块空地新建了三个居民小区,它们分别为A、B、C,且三个小区不在同一直线上,要想规划一所中学,使这所中学到三个小区的距离相等。请问同学们这所中学建在哪个位置?你怎么确定这个位置呢?
●
●
●
B
A
C
作业
练 习
1. 任意画一个三角形,然后再画这个三角形的外接圆.
2. 随意画出四点,其中任何三点都不在同一条直线上,是否一定可以画一个圆经过这四点?请举例说明.
再 见!
同课章节目录
