人教版高中物理必修一第三单元-综合受力分析专题练习(中等难度)
文档属性
| 名称 | 人教版高中物理必修一第三单元-综合受力分析专题练习(中等难度) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2024-11-12 09:31:19 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
受力分析-中等难度
一.选择题(共32小题)
1.晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,A、B两点等高,无风状态下衣服保持静止。某一时刻衣服受到水平向右的恒定风力而发生滑动,并在新的位置保持静止,如图所示。两杆间的距离为d,绳长为,衣服和衣架的总质量为m,重力加速度为g,不计绳子的质量及绳与衣架挂钩间的摩擦,sin37°=0.6。则( )
A.相比无风时,在有风的情况下∠AOB更小
B.无风时,轻绳的拉力大小为
C.衣服在新的平衡位置时,挂钩左、右两侧绳子的拉力大小不相等
D.相比于无风时,绳子拉力在有风的情况下不变
2.如图所示,粗糙水平地面上放有横截面为圆的柱状物体A,A与墙面之间放有表面光滑的圆柱形物体B,A、B均保持静止。若将A向左移动少许,下列说法正确的是( )
A.地面对A的支持力不变
B.地面对A的摩擦力不变
C.墙对B的作用力不变
D.B对A的支持力不变
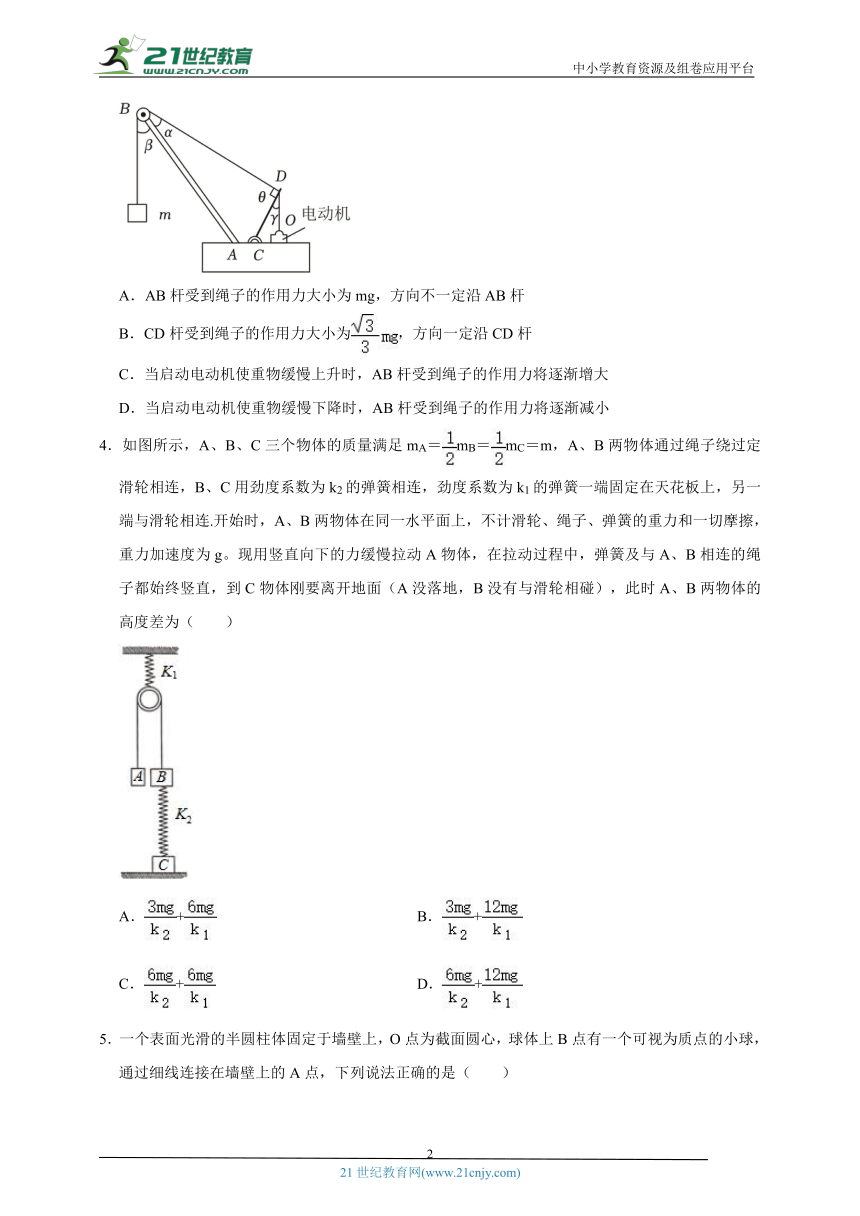
3.某兴趣小组想要运用所学力学知识进行实践研究,他们找到起重吊车的结构图,画出简化结构如图所示,AB是固定杆不可转动,B端有一光滑定滑轮;轻杆CD可绕C端自由转动,D端系着两条轻绳,一条轻绳跨过B端定滑轮连接质量为m的重物,另一轻绳缠绕在电动机转轴O上,通过电动机的牵引控制CD杆的转动从而控制重物的起落。图中所示位置两杆处于同一竖直面内,OD绳沿竖直方向,γ=30°,θ=90°,重力加速度大小为g,则( )
A.AB杆受到绳子的作用力大小为mg,方向不一定沿AB杆
B.CD杆受到绳子的作用力大小为,方向一定沿CD杆
C.当启动电动机使重物缓慢上升时,AB杆受到绳子的作用力将逐渐增大
D.当启动电动机使重物缓慢下降时,AB杆受到绳子的作用力将逐渐减小
4.如图所示,A、B、C三个物体的质量满足mA=mB=mC=m,A、B两物体通过绳子绕过定滑轮相连,B、C用劲度系数为k2的弹簧相连,劲度系数为k1的弹簧一端固定在天花板上,另一端与滑轮相连.开始时,A、B两物体在同一水平面上,不计滑轮、绳子、弹簧的重力和一切摩擦,重力加速度为g。现用竖直向下的力缓慢拉动A物体,在拉动过程中,弹簧及与A、B相连的绳子都始终竖直,到C物体刚要离开地面(A没落地,B没有与滑轮相碰),此时A、B两物体的高度差为( )
A.+ B.+
C.+ D.+
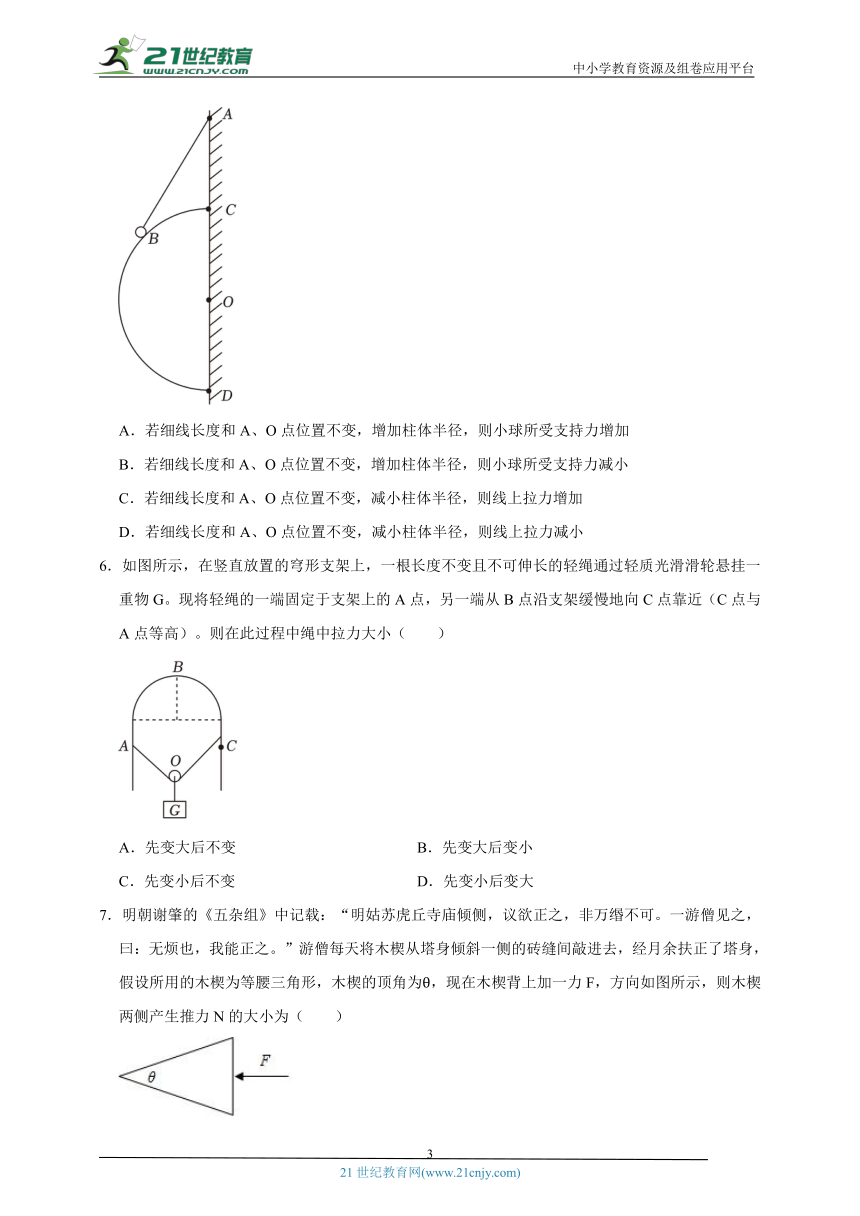
5.一个表面光滑的半圆柱体固定于墙壁上,O点为截面圆心,球体上B点有一个可视为质点的小球,通过细线连接在墙壁上的A点,下列说法正确的是( )
A.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力增加
B.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力减小
C.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力增加
D.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力减小
6.如图所示,在竖直放置的穹形支架上,一根长度不变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G。现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高)。则在此过程中绳中拉力大小( )
A.先变大后不变 B.先变大后变小
C.先变小后不变 D.先变小后变大
7.明朝谢肇的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之。”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身,假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,则木楔两侧产生推力N的大小为( )
A. B. C. D.
8.如图所示,一个内表面光滑半球形的碗放在桌面上,碗口水平,O是球心,碗的球半径为R,一根轻质杆的两端固定有A、B两个小球(可视为质点),质量分别是m1、m2,已知杆长为,杆静止时与水平面夹角为15°,则A、B两小球的质量之比是( )
A.2:1 B. C. D.
9.两个力F1和F2间的夹角为θ(0°<θ<180°),两力的合力为F,下列说法正确的是( )
A.合力F一定比分力F1和F2都大
B.若F1和F2大小不变,θ角越小,合力F越大
C.若合力F增大,θ角不变,分力F1和F2一定都增大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就增大
10.炎热的夏天,用手拧常温的碳酸饮料瓶盖时,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为( )
A.减小了瓶盖与瓶口接触面的粗糙程度
B.减小了瓶盖与瓶口螺纹间的压力
C.减小了瓶盖与瓶口接触面的接触面积
D.增大了手与瓶盖间的静摩擦力
11.如图所示,有一个小朋友,把两个半圆柱玩具甲、乙相接触并静置于水平地面上,其上有一光滑圆柱玩具丙,三者半径相同。现用水平向左的力拉甲,使甲缓慢向左移动,直至丙恰好降到地面,整个过程中乙保持静止。已知甲和乙的质量分别为3m和8m,与地面间的动摩擦因数均相同,丙的质量为4m,设最大静摩擦力等于滑动摩擦力,重力加速度为g。则下列判断正确的是( )
A.没有加拉力时,甲与地面间的摩擦力大小为2mg
B.没有加拉力时,甲对地面的压力大小为3mg
C.甲与地面间的动摩擦因数可能为0.3
D.甲与地面间的动摩擦因数可能为0.4
12.如图,倾角为θ的斜面固定在墙角,质量为M的尖劈放置在斜面上,尖劈的右侧面竖直,用轻绳系住一个质量为m的球紧靠在尖劈的右侧,轻绳与斜面平行,球与尖劈的接触面光滑,斜面对尖劈的静摩擦力恰好为0,整个系统处于静止状态。沿球心O对球施加一个水平向左的恒定推力F,系统仍处于静止状态。则( )
A.对球施加水平推力后,轻绳的拉力可能变大
B.对球施加水平推力后,尖劈对斜面的压力一定变大
C.尖劈的质量M与球的质量m之比为tan2θ
D.对球施加水平推力后,斜面对尖劈的摩擦力可能仍为0
13.一条两端固定的粗细和质量分布均匀、柔软、不可伸长的链条,在重力的作用下所具有的曲线形状,称之为悬链线.为探究其特点,现搭建如图所示的一条悬链线,经测量知两悬点A、B处切线与竖直方向夹角分别为30°和60°,两切线的交点为C,E是C点正上方链条上的点,F为悬链线的最低点,则( )
A.A、B两悬点对墙面的拉力大小之比为3:1
B.链条AF和链条FB长度之比为3:1
C.整个链条上拉力最小的点为点E
D.此时链条的重心在链条上的E点
14.如图所示,三根轻绳OA、OB、OC结于O点,OA和OB绳的另一端系于水平天花板上,OC绳C端与一重物相连,OA绳和OB绳的夹角为100°、OA绳与OC绳的夹角为120°。整个系统处于静止状态,OA绳、OB绳、OC绳上的拉力分别记为F1、F2、F3,则F1、F2、F3的大小关系正确的是( )
A.F1<F2<F3 B.F1<F3<F2 C.F2<F3<F1 D.F3<F1<F2
15.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为的小物块a相连,如图所示。质量为m的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0。从t=0时开始,对b施加沿斜面向上的拉力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。则( )
A.a、b在弹簧压缩量为处分离
B.b的加速度为
C.作用于b上的最小拉力为2mgsinθ
D.a在匀加速运动的时间为
16.如图所示,质量均为m的n(n>3)个相同匀质圆柱体依次搁置在倾角为30°的光滑斜面上,斜面底端有一竖直光滑挡板挡住使圆柱体均处于静止状态,已知重力加速度为g,则下列说法中正确的是( )
A.挡板对圆柱体1的弹力大小为
B.圆柱体1对斜面的压力大小为
C.圆柱体2对圆柱体1的压力大小为
D.若将挡板绕下端点缓慢逆时针转动60°,则转动过程中斜面对每个圆柱体的支持力均减小
17.某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.6m,b=0.1m,则物体D所受压力的大小与力F的比值为( )
A.3 B.4 C.5 D.6
18.如图所示,衣服悬挂在不可伸长的轻绳上,衣架的挂钩是光滑的,轻绳的两端固定在两根竖直杆上的A、B两点,衣服受到恒定水平向右的风力处于静止状态。保持A端位置不变,将B端分别移动到B1、B2两点。下列说法正确的是( )
A.B端移到B1,绳子张力变大
B.B端移到B1,绳子张力变小
C.B端移到B2,绳子张力变大
D.B端移到B2,绳子张力不变
19.一辆货车运载着完全相同的圆柱形光滑的空油桶,在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一个质量为m的桶C,自由地摆放在桶A、B之间。若桶A、桶B和汽车一起沿水平地面做匀速直线运动,如图所示。重力加速度大小为g,则桶A对桶C的支持力大小为( )
A.mg B.mg C.mg D.mg
20.在修建乡村住房时,工人用上了简易机械如图所示,甲站在地面上通过支架上的定滑轮拉着OA绳把建筑材料缓慢提升到楼顶后,乙再在楼顶水平拉着OB绳把建筑材料缓慢移到楼顶平台上,在乙缓慢移动建筑材料的过程中,下列说法正确的是( )
A.地面对甲的支持力变小
B.地面对甲的摩擦力变小
C.楼层对乙的作用力保持不变
D.OA绳子上的拉力先增大后减小
21.如图所示,用一轻绳通过定滑轮将质量为m的小球静置在光滑的半圆柱体上,小球的半径远小于半圆柱体截面的半径R,绳AB长度为L,长度为H的杆BC竖直且与半圆柱体边缘相切,OA与水平面夹角为θ,不计一切摩擦,重力加速度为g,下列表达式表示绳对小球的拉力F是( )
A.
B.
C.
D.
22.如图,质量为m的手机放置在支架斜面上,斜面与水平面的夹角为θ。重力加速度为g,手机始终保持静止状态。则( )
A.手机对支架的压力大小为mg,方向垂直于斜面向下
B.手机受到的摩擦力大小为mgsinθ,方向沿斜面向上
C.若θ增大,则支架对手机的摩擦力随之减小
D.若θ增大,则支架对手机的支持力保持不变
23.如图所示,一半圆形轨道放在粗糙的水平地面上,直径AB水平,轨道内表面及B端光滑,绕过B端的轻绳左端连接一小球,右端用水平力F拉轻绳,使小球在轻绳带动下从轨道最低点C开始沿轨道缓慢上滑到接近B端,轨道始终保持静止,则此过程中( )
A.地面受到轨道的静摩擦力变小
B.地面受到轨道的压力减小
C.小球对轨道的压力减小
D.轨道B端受到轻绳的作用力变小
24.如图所示,三根等长的光滑杆构成三角架,杆OA竖直放置。质量分别为m和2m的两小球用细线相连后,分别套在两杆上,在图示位置能保持静止。现将三角架绕A端在竖直平面内沿顺时针方向缓慢转动,直到AB杆水平。下列说法正确的是( )
A.OA杆对小球的弹力先增大后减小
B.OB杆对小球的弹力一直增大
C.转至AB杆水平时OB杆上的弹力大小为3mg
D.转至AB杆水平时绳上拉力为2mg
25.轻质细线上端悬挂于天花板上的O点,另一端接在质量为m的小球上,小球在水平向右的外力F作用下处于平衡状态,此时细线上的弹力大小为FT,细线与竖直方向的夹角为θ、与F的夹角为α,如图所示。以下判断正确的是( )
A.保持F水平,逐渐缓慢减小θ,则F、FT都逐渐增大
B.若换一根更长的细线,保持θ、α不变,F、FT可能都减小
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,则FT逐渐减小,F先增大后减小
D.保持小球位置不变,F沿逆时针方向缓慢转动直至F竖直向上,则F先减小后增大
26.如图所示,倾角为30°的斜面顶端竖直固定一光滑的定滑轮,工人师傅用轻绳通过定滑轮牵引斜面底端的重物(可视为质点),此时连接重物的轻绳与水平面的夹角为45°,重物与斜面间的动摩擦因数μ=。在重物缓慢被牵引到斜面顶端的过程中,轻绳拉力F、重物所受摩擦力f的大小变化情况是( )
A.拉力F先减小再增大
B.拉力F逐渐减小
C.摩擦力f先减小再增大
D.摩擦力f先增大再减小
27.如图所示,一圆环套在固定的倾斜光滑杆AB上,轻绳绕过光滑定滑轮与圆环相连,整个装置处于同一竖直平面内,用力F拉动轻绳使圆环从图示位置沿杆向上缓慢运动,圆环对杆的弹力大小为FN,在圆环运动过程中,下列说法正确的是( )
A.F一直增大,FN一直减小
B.F一直增大,FN先减小后增大
C.F先减小后增大,FN一直增大
D.F先减小后增大,FN先减小后增大
28.春节期间,人们挂起红灯笼,来营造一种喜庆的氛围.如图所示,轻绳a、b将灯笼悬挂于O点保持静止,绳a与水平方向的夹角为θ,绳b水平。现保持O点位置不变,b绳缓慢逆时针转动到竖直,则( )
A.轻绳a的作用力减小,轻绳b的作用力先减小后增大
B.轻绳a、b的作用力均减小
C.轻绳a、b的作用力均增大
D.轻绳a的作用力不变,轻绳b的作用力先减小后增大
29.如图所示,粗糙的水平地面上放置一物块,物块左边受到弹簧的斜向上且与水平面成θ角的拉力作用,右侧受到水平向右的拉力F作用,物块处于静止状态。若将水平向右的拉力大小变为F+ΔF,物块仍保持静止,则下列说法正确的是( )
A.弹簧的弹力一定变大
B.物块受到地面的摩擦力的大小可能不变
C.地面对物块的支持力可能变大
D.弹簧弹力和地面对物块的支持力以及拉力F的合力一定变大
30.如图所示,把一重为G的物体用一水平方向的推力F=kt(k为恒量,t为时间)压在竖直的足够高的平整墙上,从t=0开始物体所受的摩擦力f随t变化的关系是图中的( )
A. B.
C. D.
31.在中学秋季田径运动会上,高一2班李好同学奋力拼搏,勇夺男子100m冠军,下图为该同学奔跑途中的两个瞬间,用Ff1、Ff2分别表示该同学在图甲、乙两瞬间所受到的摩擦力,则关于Ff1、Ff2的方向,以下说法正确的是( )
A.Ff1向后,Ff2向后 B.Ff1向前,Ff2向前
C.Ff1向前,Ff2向后 D.Ff1向后,Ff2向前
32.如图所示,有一小球被轻绳拴住悬挂在天花板上并放置在斜面上,已知轻绳与竖直方向的夹角为45°,斜面倾角为37°,所有接触面都是光滑的,在斜面上施加一水平外力,使整个装置开始处于静止状态。现水平向左缓慢移动斜面,直至轻绳到达竖直位置,该过程中小球一直在斜面上,小球视为质点。下列说法正确的是( )
A.斜面开始静止时,轻绳对小球的拉力大小等于斜面对小球的支持力大小
B.斜面缓慢移动过程中,斜面对小球的支持力先增大后减小
C.斜面缓慢移动过程中,轻绳对小球的拉力一直增大
D.斜面缓慢移动过程中,斜面对水平面的压力一直不变
二.解答题(共3小题)
33.如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:
(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
34.如图所示,质量为m1的物体A压在放于地面上的竖直轻弹簧k1上,上端与轻弹簧k2相连,轻弹簧k2上端与质量为m2物体B相连,物体B通过轻绳跨过光滑的定滑轮与轻质小桶P相连,A、B均静止.现缓慢地向小桶P内加入细砂,当弹簧k1恰好恢复原长时,(小桶一直未落地)求
(1)小桶P内所加入的细砂质量;
(2)小桶在此过程中下降的距离.
35.如图所示,一劲度系数为k1的弹簧,竖直地固定在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计。要使下面弹簧的弹力减为原来的时,应将上面弹簧的上端A竖直向上提高多少?
受力分析-中等难度
参考答案与试题解析
一.选择题(共32小题)
1.晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,A、B两点等高,无风状态下衣服保持静止。某一时刻衣服受到水平向右的恒定风力而发生滑动,并在新的位置保持静止,如图所示。两杆间的距离为d,绳长为,衣服和衣架的总质量为m,重力加速度为g,不计绳子的质量及绳与衣架挂钩间的摩擦,sin37°=0.6。则( )
A.相比无风时,在有风的情况下∠AOB更小
B.无风时,轻绳的拉力大小为
C.衣服在新的平衡位置时,挂钩左、右两侧绳子的拉力大小不相等
D.相比于无风时,绳子拉力在有风的情况下不变
【分析】根据受力情况和几何关系,分析角度;动滑轮两端绳子的拉力总是相等;根据平衡条件和几何关系,分析F。
【解答】解:A.设无风时绳子夹角的一半为θ1,绳长为L,有风时绳子夹角的一半为θ2,钩子两边细绳与竖直方向夹角相等,则有风时如图
则有:L1+L2=Lsinθ2;d=Lsinθ1
又因为:d>L1+L2
所以:θ1>θ2
故A正确;
B.无风时,由几何关系有:
解得:θ1=37°
根据平衡条件有:mg=2Fcosθ1
解得轻绳的拉力大小:
故B错误;
C.不计绳子的质量及绳与衣架挂钩间的摩擦,则绳子的拉力总是相等,故C错误;
D.在有风的情况下,设重力与风力的合力F合与竖直方向的夹角为θ3,则有:
F合=
根据平衡条件有:F合=2F′cosθ2
解得轻绳的拉力大小:
与无风时的F=相比,θ1>θ2>θ3,可知相比于无风时,绳子拉力在有风的情况下不一定不变,故D错误。
故选:A。
2.如图所示,粗糙水平地面上放有横截面为圆的柱状物体A,A与墙面之间放有表面光滑的圆柱形物体B,A、B均保持静止。若将A向左移动少许,下列说法正确的是( )
A.地面对A的支持力不变
B.地面对A的摩擦力不变
C.墙对B的作用力不变
D.B对A的支持力不变
【分析】利用整体与隔离法、力的合成与分解法对本题进行求解。
【解答】如图,A的重力为GA,B的重力为GB,地面对A的支持力为F,地面对A的摩擦力为f,B对A的作用力为FBA,与水平方向的夹角为θ,A对B的作用力为FAB,与水平方向的夹角为θ,墙面对B的作用力为FB。
解:A.由整体分析可知,A、B保持静止时地面对A的支持力等于A与B的重力之和,将A向左移动少许,A、B仍将保持静止,因此地面对A的支持力不变,故A正确;
B.如图,对A进行受力分析可知f=FBAcosθ,又有FBA=FAB,且FABsinθ=GB,因此有f=GB,将A向左移动,θ增大,f减小,故B错误;
C.由整体分析可知,墙面对B的作用力等于地面对A的摩擦力,已知地面对A的摩擦力减小,故C错误;
D.B对A的作用力FBA=,θ增大,FBA减小,故D错误。
故选:A。
3.某兴趣小组想要运用所学力学知识进行实践研究,他们找到起重吊车的结构图,画出简化结构如图所示,AB是固定杆不可转动,B端有一光滑定滑轮;轻杆CD可绕C端自由转动,D端系着两条轻绳,一条轻绳跨过B端定滑轮连接质量为m的重物,另一轻绳缠绕在电动机转轴O上,通过电动机的牵引控制CD杆的转动从而控制重物的起落。图中所示位置两杆处于同一竖直面内,OD绳沿竖直方向,γ=30°,θ=90°,重力加速度大小为g,则( )
A.AB杆受到绳子的作用力大小为mg,方向不一定沿AB杆
B.CD杆受到绳子的作用力大小为,方向一定沿CD杆
C.当启动电动机使重物缓慢上升时,AB杆受到绳子的作用力将逐渐增大
D.当启动电动机使重物缓慢下降时,AB杆受到绳子的作用力将逐渐减小
【分析】绳对杆的作用力的方向是沿着绳的方向,那么将绳对杆的力分解后求合力。
【解答】解:A.杆AB固定于平台,杆力不一定沿杆,同一条绳的力大小相等,其合力一定在其角平分线上,由于杆的力不一定沿杆,如图所示
两个力T所作力的平行四边形为菱形,根据平衡条件可得
T=mg
根据几何关系可得
a+β=60°
对角线为F杆,则AB杆受到绳子的作用力大小为
F杆=2Tcos30°=mg
故A错误;
B.根据题意D端连接两条轻绳,两条轻绳的力不一定大小相等,且CD杆为铰链连接,为“活”杆,杆力沿着杆的方向,水平方向,根据
F'杆cos60°=Tcos30°=mgcos30°
解得
F'杆=mg
故B错误;
CD.当启动电动机使重物缓慢下降时,即T=mg不变,∠DBM变小,根据
F杆=2Tcos
可知F杆增大,故C正确,D错误。
故选:C。
4.如图所示,A、B、C三个物体的质量满足mA=mB=mC=m,A、B两物体通过绳子绕过定滑轮相连,B、C用劲度系数为k2的弹簧相连,劲度系数为k1的弹簧一端固定在天花板上,另一端与滑轮相连.开始时,A、B两物体在同一水平面上,不计滑轮、绳子、弹簧的重力和一切摩擦,重力加速度为g。现用竖直向下的力缓慢拉动A物体,在拉动过程中,弹簧及与A、B相连的绳子都始终竖直,到C物体刚要离开地面(A没落地,B没有与滑轮相碰),此时A、B两物体的高度差为( )
A.+ B.+
C.+ D.+
【分析】分别求出初状态两根弹簧的形变量,再求出末状态两根弹簧的形变量,根据位移关系求解A、B两物体的高度差。
【解答】解:设开始BC间弹簧的压缩量为x1,上面的弹簧伸长量为x′1,绳子拉力为T;
对物体A根据平衡条件可得:T=mg;
对B物体根据平衡条件可得:2mg=k2x1+T
解得:x1=;
对滑轮根据平衡条件可得:2T=k1x′1
解得:x′1=;
设C物体刚要离开地面时BC间弹簧的伸长量为x2,上面的弹簧伸长量为x′2,绳子拉力为T′;
对物体C根据平衡条件可得:2mg=k2x2
解得:x2=;
C物体刚要离地时,上端弹簧的拉力为T′=8mg
对滑轮根据平衡条件可得:8mg=k1x′2
解得:x′2=。
所以此过程中A下降的高度为:hA=x1+x2+2(x′2﹣x′1)=+
此过程中B物体上升的高度:hB=x1+x2=
此时A、B两物体的高度差为Δh=hA+hB=+,故D正确、ABC错误。
故选:D。
5.一个表面光滑的半圆柱体固定于墙壁上,O点为截面圆心,球体上B点有一个可视为质点的小球,通过细线连接在墙壁上的A点,下列说法正确的是( )
A.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力增加
B.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力减小
C.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力增加
D.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力减小
【分析】对小球进行受力分析,做出力的矢量三角形,根据几何三角形和力三角形相似,分析力的大小变化。
【解答】解:对小球进行受力分析,可知它受重力G,柱体给它的支持力FN,细线中拉力FT,做出力的矢量三角形如图所示
根据相似性则有
AB.增加柱体半径,即OB增加,所以小球所受的支持力增加;减小柱体半径,小球所受的支持力减小,故A正确,B错误;
CD.增加或减小柱体半径,但是细线长度AB不变,拉力不变,故CD错误。
故选:A。
6.如图所示,在竖直放置的穹形支架上,一根长度不变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G。现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高)。则在此过程中绳中拉力大小( )
A.先变大后不变 B.先变大后变小
C.先变小后不变 D.先变小后变大
【分析】当轻绳的右端从B点移到直杆最上端时,两绳的夹角增大.滑轮两侧绳子的拉力大小相等,方向关于竖直方向对称.以滑轮为研究对象,根据平衡条件研究绳的拉力变化情况.当轻绳的右端从直杆的最上端移到C点的过程中,根据几何知识分析得到滑轮两侧绳子的夹角不变,由平衡条件判断出绳子的拉力保持不变。
【解答】解:当轻绳的右端从B点移到直杆最上端D时,设两绳的夹角为2θ.以滑轮为研究对象,分析受力情况,作出力图如图1所示。根据平衡条件得
2Fcosθ=mg
得到绳子的拉力F=
所以在轻绳的右端从B点移到直杆最上端时D的过程中,θ增大,cosθ减小,则F变大;
当轻绳的右端从直杆最上端的D点移到C点时,设两绳的夹角为2α。
设绳子总长为L,两直杆间的距离为s,由数学知识得到
sinα=,L、S不变,则α保持不变。
再根据平衡条件可知,两绳的拉力F保持不变。
所以绳中拉力大小变化的情况是先变大后不变。故BCD错误,A正确。
故选:A。
7.明朝谢肇的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之。”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身,假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,则木楔两侧产生推力N的大小为( )
A. B. C. D.
【分析】由于木楔处在静止状态,可将力F沿与木楔的斜面垂直且向上的方向进行分解,根据平行四边形定则,画出力F按效果分解的图示。并且可据此求出木楔两侧产生的推力,再进行分析。
【解答】解:选木楔为研究对象,木楔受到的力有:水平向左的F和两侧给它的与木楔的斜面垂直的弹力,由于木楔处于平衡状态,所以两侧给木楔的斜面垂直的弹力与F沿两侧分解的力是相等的,力F的分解如图:
则F=F1cos(90°﹣ )+F2cos(90°﹣ )=2F1cos(90°﹣)=2F1sin
N=F1
故得N=,故ABD错误,C正确。
故选:C。
8.如图所示,一个内表面光滑半球形的碗放在桌面上,碗口水平,O是球心,碗的球半径为R,一根轻质杆的两端固定有A、B两个小球(可视为质点),质量分别是m1、m2,已知杆长为,杆静止时与水平面夹角为15°,则A、B两小球的质量之比是( )
A.2:1 B. C. D.
【分析】先对两小球和杆组成的系统作为研究对象,根据受力分析解得碗对A、B的作用力,再隔离分析可知A、B两球的质量之比。
【解答】解:由几何关系可知OA、OB的夹角为90°,OB与水平方向的夹角为30°,OA与水平方向的夹角为60°,选取两小球和杆作为研究对象,受力分析如下图所示
由平衡条件得,F1在水平方向的分力F'和F2在水平方向的分力F''相等,即
F1cos60°=F2cos30°
所以
=
在以小球1为研究对象,受力分析如下图所示
根据平衡条件得F与m1g的合力与F1等大反向,图中两个阴影三角形相似,则得
再以小球2为研究对象得
则得
解得
故B正确,ACD错误。
故选:B。
9.两个力F1和F2间的夹角为θ(0°<θ<180°),两力的合力为F,下列说法正确的是( )
A.合力F一定比分力F1和F2都大
B.若F1和F2大小不变,θ角越小,合力F越大
C.若合力F增大,θ角不变,分力F1和F2一定都增大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就增大
【分析】力是矢量,有大小、方向,遵循平行四边形定则;合力的范围:|F1﹣F2|<F合≤F1+F2,据此结合实际分析合力与分力的关系即可。
【解答】解:A:由力的合成方法可知,两力合力的范围|F1﹣F2|<F合≤F1+F2,所以合力有可能大于任一分力,也可能小于任一分力,还可能与两个分力都相等,故A错误;
B:若F1和F2大小不变,力的合成遵循平行四边形定则,θ角越小,合力F越大,故B正确;
C:如果夹角θ不变,F1大小不变,F2增大,合力F可以减小,也可以增大,故C错误;
D:如果夹角θ不变,F1大小不变,只要F2增大,合力F可以减小,也可以增大,故D错误。
故选:B。
10.炎热的夏天,用手拧常温的碳酸饮料瓶盖时,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为( )
A.减小了瓶盖与瓶口接触面的粗糙程度
B.减小了瓶盖与瓶口螺纹间的压力
C.减小了瓶盖与瓶口接触面的接触面积
D.增大了手与瓶盖间的静摩擦力
【分析】依据滑动摩擦力大小由动摩擦因数及压力有关,与接触面积无关,从而即可分析。
【解答】解:ABC、常温下的碳酸饮料对瓶盖有压力,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为减小了瓶盖与瓶口螺纹间的压力,从而减小瓶盖与瓶口的滑动摩擦力,并没有改变瓶盖与瓶口接触面的粗糙程度,同时瓶盖与瓶口的滑动摩擦力大小与接触面的接触面积大小无关,故AC错误,B正确;
D、手在水平拧塑料瓶盖的同时再向下压瓶盖,增大了手与瓶盖间的静摩擦力,但能更容易将瓶盖拧开,与其无关,故D错误;
故选:B。
11.如图所示,有一个小朋友,把两个半圆柱玩具甲、乙相接触并静置于水平地面上,其上有一光滑圆柱玩具丙,三者半径相同。现用水平向左的力拉甲,使甲缓慢向左移动,直至丙恰好降到地面,整个过程中乙保持静止。已知甲和乙的质量分别为3m和8m,与地面间的动摩擦因数均相同,丙的质量为4m,设最大静摩擦力等于滑动摩擦力,重力加速度为g。则下列判断正确的是( )
A.没有加拉力时,甲与地面间的摩擦力大小为2mg
B.没有加拉力时,甲对地面的压力大小为3mg
C.甲与地面间的动摩擦因数可能为0.3
D.甲与地面间的动摩擦因数可能为0.4
【分析】根据对称性画出受力分析图,根据共点力的平衡条件求解甲与地面摩擦力,结合牛顿第三定律解得压力;先求出没有拉力时甲、乙两半圆柱体半径中心之间的距离,丙恰好降到地面时,求出此时甲半圆柱体半径重心与丙圆柱体中心连线与地面夹角为θ,根据共点力平衡条件分析动摩擦因数的范围,从而分析CD。
【解答】解:AB.对丙受力分析,如图1所示
图1
根据共点力平衡条件结合几何关系可知弹力和竖直方向的夹角θ=30°,故
地面对甲的摩擦力大小为f,对甲受力分析,如图2所示
图2
根据共点力平衡,水平方向上
f=Fsinθ
解得
在竖直方向上
故AB错误;
CD.丙恰好降到地面时,甲和乙与丙之间的相互作用力最大为Fm,甲和乙恰好不相对地面滑动,对丙受力分析,如图3所示
图3
由几何关系可知Fm 与竖直方向的夹角α=60°,根据共点力平衡,可得
2Fmcos60°=4mg
解得
Fm=4mg
对乙受力分析如图4所示
图4
最大静摩擦力至少为
竖直方向上
N=8mg+F′msin30°=10mg
根据摩擦力公式有
fmax=μminN
解得
故C错误,D正确。
故选:D。
12.如图,倾角为θ的斜面固定在墙角,质量为M的尖劈放置在斜面上,尖劈的右侧面竖直,用轻绳系住一个质量为m的球紧靠在尖劈的右侧,轻绳与斜面平行,球与尖劈的接触面光滑,斜面对尖劈的静摩擦力恰好为0,整个系统处于静止状态。沿球心O对球施加一个水平向左的恒定推力F,系统仍处于静止状态。则( )
A.对球施加水平推力后,轻绳的拉力可能变大
B.对球施加水平推力后,尖劈对斜面的压力一定变大
C.尖劈的质量M与球的质量m之比为tan2θ
D.对球施加水平推力后,斜面对尖劈的摩擦力可能仍为0
【分析】以尖劈和球整体为研究对象,再以球为研究对象,根据共点力平衡条件分析尖劈和小球的质量关系,对球施加推力后,再对整体分析斜面对尖劈的摩擦力和尖劈对斜面的压力的变化。
【解答】解:C.对球施加水平推力前,以尖劈和球整体为研究对象,如图1,可知轻绳的拉力
T=(M+m )gsinθ
斜面对尖劈的支持力
N1=(M+m)gcosθ
以球为研究对象,如图2,可知轻绳的拉力
T=
联立解得
=
故C错误。
A.以球为研究对象,可知对球施加水平推力后不影响竖直方向力的大小,轻绳的拉力不变,如图3,故A错误;
BD.以尖劈和球整体为研究对象,对球施加水平推后,如图4,有
N'1=(M+m)gcosθ+Fsinθ
总重力不变,可得斜面对尖劈的弹力变大,即尖劈对斜面的压力变大;轻绳拉力T不变,总重力不变,施加推力F后,要保持平衡,有
T+Fcosθ=(M+m)gsinθ+f
则斜面对尖劈的摩擦力沿斜面向下,斜面对尖劈的摩擦力不可能为0,故B正确,D错误。
故选:B。
13.一条两端固定的粗细和质量分布均匀、柔软、不可伸长的链条,在重力的作用下所具有的曲线形状,称之为悬链线.为探究其特点,现搭建如图所示的一条悬链线,经测量知两悬点A、B处切线与竖直方向夹角分别为30°和60°,两切线的交点为C,E是C点正上方链条上的点,F为悬链线的最低点,则( )
A.A、B两悬点对墙面的拉力大小之比为3:1
B.链条AF和链条FB长度之比为3:1
C.整个链条上拉力最小的点为点E
D.此时链条的重心在链条上的E点
【分析】根据“三力汇交”原理对悬链线受力分析,再根据共点力的平衡条件分析求解两悬点处墙壁对链条的拉力大小之比,根据牛顿第三定律求解链条对墙面的拉力大小之比;对两部分链条进行受力分析,根据平衡条件求解两部分链条的质量之比,再求长度之比;在链条上任取一点D(除F外),取D与F点之间这一部分链条为对象,根据平衡条件分析作答;根据“三力汇交”原理可知E点在重力作用线上,再根据链条的形状分析重心的位置。
【解答】解:A.对悬链线受力分析,两悬点A、B处切线与竖直方向夹角分别为30°和60°,受力分析图如图1所示:
根据平衡条件TA=mgcos30°
TB=mgcos60°
代入数据联立解得,A、B两悬点处墙壁对链条的拉力大小之比为:1
根据牛顿第三定律,A、B两悬点链条对墙面的拉力大小之比:1,故A错误;
B.设最低点F处的张力为T,左侧悬链质量为m1,右侧质量为m2,两部分链条的受力图如图2所示:
根据平衡条件,对左侧悬链m1g=
对右侧悬链m2g=
得两部分链条的质量之比=3
链条AF和链条FB长度之比为3:1,故B正确;
C.在链条上任取一点D(除F外),取D与F点之间这一部分链条为对象,质量为Δm,D点的张力为TD
由于F点的张力处于水平方向,根据平衡条件结合数学知识TD=>T
可知整个链条上拉力最小的点为最低点F,故C错误;
D.根据“三力汇交”原理,由题意可知,重力作用线经过E点,但由于链条形状不规则,重心不在链条的E点,故D错误。
故选:B。
14.如图所示,三根轻绳OA、OB、OC结于O点,OA和OB绳的另一端系于水平天花板上,OC绳C端与一重物相连,OA绳和OB绳的夹角为100°、OA绳与OC绳的夹角为120°。整个系统处于静止状态,OA绳、OB绳、OC绳上的拉力分别记为F1、F2、F3,则F1、F2、F3的大小关系正确的是( )
A.F1<F2<F3 B.F1<F3<F2 C.F2<F3<F1 D.F3<F1<F2
【分析】结点O受力平衡,做出O点受力分析图,结合正弦定理即可求解。
【解答】解:对节点O进行受力分析如图所示
根据正弦定理
可知 F1<F2<F3,故A正确,BCD错误。
故选:A。
15.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为的小物块a相连,如图所示。质量为m的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0。从t=0时开始,对b施加沿斜面向上的拉力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。则( )
A.a、b在弹簧压缩量为处分离
B.b的加速度为
C.作用于b上的最小拉力为2mgsinθ
D.a在匀加速运动的时间为
【分析】A、根据初速为0的匀变加直线运动推论:连续相等时间间隔内位移之比1:3:5……计算分离的位置;
B、两物体刚好要分离,即a与b之间无相互作用力,对a由牛顿第二定律,求出分离时的加速度;
C、分离前对整体分析可知,由牛顿第二定律分析出刚开始运动时拉力最小,进而求出最小拉力;
D、分离前a在匀加速运动,通过位移求时间。
【解答】解:A、由于初速度为0,b在分离前位移x1和分离后相等时间内位移x2之比为:
且由题可知:x1+x2=x0
解得:
初始时压缩量为x0,分离前位移,即压缩量减小,可得a、b在弹簧压缩量为时分离,故A错误;
B、两物体刚好要分离时a与b之间无相互作用力,对a由牛顿第二定律可得
初始时小物体b紧靠a静止在斜面上,将二者看成一个整体,可知弹力大小与整体重力的分力大小相等,有
kx0=(+m)gsinθ
解得:a=gsinθ,故B错误;
C、分离前对整体分析可知,由牛顿第二定律有
则刚开始运动时拉力最小,则Δx=x0,且
可得:,故C错误;
D、a与b在b向上运动的位移刚好分离,此前a在匀加速运动,则有:
解得:,故D正确。
故选:D。
16.如图所示,质量均为m的n(n>3)个相同匀质圆柱体依次搁置在倾角为30°的光滑斜面上,斜面底端有一竖直光滑挡板挡住使圆柱体均处于静止状态,已知重力加速度为g,则下列说法中正确的是( )
A.挡板对圆柱体1的弹力大小为
B.圆柱体1对斜面的压力大小为
C.圆柱体2对圆柱体1的压力大小为
D.若将挡板绕下端点缓慢逆时针转动60°,则转动过程中斜面对每个圆柱体的支持力均减小
【分析】小球对挡板和对斜面的压力不好求,我们可以求挡板和斜面对小球的支持力,利用牛顿第三定律求解这两个力,小球静止,对小球受力分析后应用平衡条件列式求解。
【解答】解:A、以整体为研究对象,受力情况如图所示:
挡板对圆柱体1的弹力大小为T=nmgtan30°=,故A错误;
B、以圆柱体1为研究对象,受力如图,则:
沿斜面的方向:N′+mgsin30°=N2cos30°
垂直于斜面的方向:N1=N2sin30°+mgcos30°
所以N1=.根据牛顿第三定律可得圆柱体1对斜面的压力大小为,故B正确;
C、选取除1以外的所有圆柱体为研究对象,整体受到重力、斜面从支持力和圆柱体1的支持力,根据共点力平衡的条件可知,整体受到的1的支持力与整体的重力沿斜面方向的分力大小相等,方向相反,所以:N21=(n﹣1)mgsin30°=mg,根据牛顿第三定律可得,圆柱体2对圆柱体1的压力大小为mg,故C错误;
D、若将挡板绕下端点缓慢逆时针转动60°,圆柱体2到圆柱体n受力情况不变,则转动过程中斜面对2到n圆柱体的支持力均不变,故D错误。
故选:B。
17.某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.6m,b=0.1m,则物体D所受压力的大小与力F的比值为( )
A.3 B.4 C.5 D.6
【分析】根据力F的作用效果将它分解,再将AC所受压力的作用效果进行分解,根据数学知识求出物体D所受压力的大小是F的多少倍。
【解答】解:设力F与水平方向的夹角为θ,将力F按作用效果沿AB和AC两个方向进行分解,作出力的分解图如图甲所示。则有:
2F1cosθ=F
则得 F1=F2= 再将F2按作用效果分解为FN和FN′,作出力的分解图如图乙所示。
则有:
FN=F2sinθ
联立得到:FN=
根据几何知识得可知tanθ==6;
得到:FN=3F,故A正确,BCD错误;
故选:A。
18.如图所示,衣服悬挂在不可伸长的轻绳上,衣架的挂钩是光滑的,轻绳的两端固定在两根竖直杆上的A、B两点,衣服受到恒定水平向右的风力处于静止状态。保持A端位置不变,将B端分别移动到B1、B2两点。下列说法正确的是( )
A.B端移到B1,绳子张力变大
B.B端移到B1,绳子张力变小
C.B端移到B2,绳子张力变大
D.B端移到B2,绳子张力不变
【分析】对挂钩受力分析,根据平衡条件结合几何关系列式求解;注意确定悬点从B上移或下移,细线与杆的夹角的变化。
【解答】解:对挂钩受力分析,如图所示,将重力G与风力F合成为等效重力G′,两段绳的拉力T等大,其合力与等效重力G′等大反向。
过A、B分别做平行于G′的直线a、b(直线a、b为等效的晾衣杆),直线a、b之间的距离为c,设绳子与直线a、b的夹角为θ。
由几何关系和平衡条件可得:2Tcosθ=G′
将B端移动到B1点,相当于将直线b平移到直线b1,即直线a、b之间的距离变大(等效的晾衣杆距离变大),绳子总长度一定,由几何关系可知,θ较变大,cosθ变小,则T增大。
同理,将B端移动到B2点,相当于将直线b平移到直线b2,即直线a、b之间的距离变小(等效的晾衣杆距离变小),绳子总长度一定,由几何关系可知,θ较变小,cosθ变大,则T减小。
故A正确,BCD错误。
故选:A。
19.一辆货车运载着完全相同的圆柱形光滑的空油桶,在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一个质量为m的桶C,自由地摆放在桶A、B之间。若桶A、桶B和汽车一起沿水平地面做匀速直线运动,如图所示。重力加速度大小为g,则桶A对桶C的支持力大小为( )
A.mg B.mg C.mg D.mg
【分析】对球C进行受力分析,根据共点力平衡、力的合成以及数学知识解决问题
【解答】解:对物体C受力分析,受重力、A和B对C的弹力
根据几何知识:弹力与竖直方向的夹角为30°
根据平衡条件得到:
,故ACD错误,B正确。
故选:B。
20.在修建乡村住房时,工人用上了简易机械如图所示,甲站在地面上通过支架上的定滑轮拉着OA绳把建筑材料缓慢提升到楼顶后,乙再在楼顶水平拉着OB绳把建筑材料缓慢移到楼顶平台上,在乙缓慢移动建筑材料的过程中,下列说法正确的是( )
A.地面对甲的支持力变小
B.地面对甲的摩擦力变小
C.楼层对乙的作用力保持不变
D.OA绳子上的拉力先增大后减小
【分析】根据受力平衡分析乙移动建筑材料的过程中,可知滑轮与乙这一侧绳子OC与竖直方向的夹角θ逐渐变大,根据平衡条件分析拉力的变化,对甲根据共点力平衡条件分析,甲与地面的摩擦力、支持力的变化,对乙,根据力的合成分析楼层对乙的作用力。
【解答】解:D.设建筑材料的重力为G,OA绳对建筑材料的拉力为FOA,乙对OB绳的拉力大小为FOB,如图1
图1
根据平衡条件有FOA=
θ增大,则FOA增大,故D错误;
B.对甲受力分析,由平衡条件可知,甲与地面之间的摩擦力大小等于OA绳对甲的拉力在水平方上的分力,由于OA绳对甲的拉力逐渐增大且OA绳与水平方向夹角不变,所以可得甲与地面之间的摩擦力逐渐增大,故B错误;
A.对甲受力分析,竖直方向由平衡条件可知,N+FOAsinα=m甲g,可知地面对甲的支持力变小,故A正确;
C.对乙受力分析,如图2
图2
乙受到的支持力与自身重力大小相等,摩擦力与OB绳上的拉力大小相等,由于OB绳上的拉力变大,所以摩擦力变大,摩擦力与支持力的合力变大,由平行四边定则合力方向变化,则楼层对乙的作用力方向变化,大小变大,故C错误。
故选:A。
21.如图所示,用一轻绳通过定滑轮将质量为m的小球静置在光滑的半圆柱体上,小球的半径远小于半圆柱体截面的半径R,绳AB长度为L,长度为H的杆BC竖直且与半圆柱体边缘相切,OA与水平面夹角为θ,不计一切摩擦,重力加速度为g,下列表达式表示绳对小球的拉力F是( )
A.
B.
C.
D.
【分析】对小球受力分析,根据力的矢量三角形与几何三角形的相似性解答。
【解答】解:对小球受力分析,受重力、支持力和拉力,如图所示
根据相似性有:
=
解得
F=
故C正确,ABD错误;
故选:C。
22.如图,质量为m的手机放置在支架斜面上,斜面与水平面的夹角为θ。重力加速度为g,手机始终保持静止状态。则( )
A.手机对支架的压力大小为mg,方向垂直于斜面向下
B.手机受到的摩擦力大小为mgsinθ,方向沿斜面向上
C.若θ增大,则支架对手机的摩擦力随之减小
D.若θ增大,则支架对手机的支持力保持不变
【分析】对手机受力分析,根据平衡条件列式求解手机所受支持力和摩擦力,判断其随θ的变化;支架对手机的作用力与重力等大反向。
【解答】解:AB.手机处于静止状态,对手机受力分析,设手机受到的支持力为N,摩擦力为f
根据共点力平衡条件有
N=mgcosθ
f=mgsinθ
根据牛顿第三定律可知手机对支架的压力大小与手机受到的支持力大小相等,为mgcosθ,方向垂直于斜面向下。手机受到的摩擦力大小为mgsinθ,方向沿斜面向上,故A错误,B正确;
CD.若θ增大,sinθ增大,cosθ减小,则支架对手机的摩擦力随之增大,支架对手机的支持力减小,故CD错误;
故选:B。
23.如图所示,一半圆形轨道放在粗糙的水平地面上,直径AB水平,轨道内表面及B端光滑,绕过B端的轻绳左端连接一小球,右端用水平力F拉轻绳,使小球在轻绳带动下从轨道最低点C开始沿轨道缓慢上滑到接近B端,轨道始终保持静止,则此过程中( )
A.地面受到轨道的静摩擦力变小
B.地面受到轨道的压力减小
C.小球对轨道的压力减小
D.轨道B端受到轻绳的作用力变小
【分析】对整体受力分析可知地面受轨道压力的变化情况,对小球受力分析,根据正弦定理与几何关系可分析ACD项。
【解答】解:B.对小球、轨道整体,由受力平衡知地面对轨道的静摩擦力大小为f=F,地面对轨道的支持力N1与小球和轨道的总重力平衡,即N1不变,根据牛顿第三定律知地面受到轨道的压力不变,故B错误;
AC.小球受力情况如图所示:
设轨道对小球的支持力大小为N2,与竖直方向夹角为θ,轻绳与竖直方向夹角为α,有
﹣θ+2 (θ+α)=π
即θ=﹣2α
根据正弦定理有
==
可得
N2=mgtanα
F=mg=mg (2cosα﹣)
α从45°逐渐减小,则N2将减小,F将增大,地面受到轨道的静摩擦力变大,故A错误,C正确;
D.由于B端两侧轻绳的夹角减小且F增大,轨道B端受到轻绳的作用力增大,故D错误。
故选:C。
24.如图所示,三根等长的光滑杆构成三角架,杆OA竖直放置。质量分别为m和2m的两小球用细线相连后,分别套在两杆上,在图示位置能保持静止。现将三角架绕A端在竖直平面内沿顺时针方向缓慢转动,直到AB杆水平。下列说法正确的是( )
A.OA杆对小球的弹力先增大后减小
B.OB杆对小球的弹力一直增大
C.转至AB杆水平时OB杆上的弹力大小为3mg
D.转至AB杆水平时绳上拉力为2mg
【分析】根据整体分析法画力的矢量三角形,结合几何关系分析杆对小球的弹力变化,根据几何关系解得CD项。
【解答】解:AB.将两小球看成一个整体,构建整体受力的矢量三角形,如图1所示:
图1
两弹力间的夹角大小不变,整体重力大小方向均不变,可构造该矢量三角形的外接圆,在OA杆对小球的弹力方向由水平变化的过程中,OA杆对小球的弹力逐渐增大,OB杆对小球的弹力一直减小。故AB错误;
CD.末状态时,N1、N2间的夹角为120°,N1、N2与竖直方向的夹角均为60°,如图2
图2
根据合成规律可知末态时两杆对球的弹力大小相等,均为3mg。
以OA杆上的小球为研究对象,根据余弦定理
cos60°=
可得细绳对小球的作用力
T=mg
故C正确,D错误。
故选:C。
25.轻质细线上端悬挂于天花板上的O点,另一端接在质量为m的小球上,小球在水平向右的外力F作用下处于平衡状态,此时细线上的弹力大小为FT,细线与竖直方向的夹角为θ、与F的夹角为α,如图所示。以下判断正确的是( )
A.保持F水平,逐渐缓慢减小θ,则F、FT都逐渐增大
B.若换一根更长的细线,保持θ、α不变,F、FT可能都减小
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,则FT逐渐减小,F先增大后减小
D.保持小球位置不变,F沿逆时针方向缓慢转动直至F竖直向上,则F先减小后增大
【分析】根据共点力平衡条件列式分析F、FT的大小变化,绳长对力的大小无影响,根据力的矢量合成图分析CD项。
【解答】解:A.保持F水平,逐渐缓慢减小θ,对小球受力分析有FTcosθ=mg,F=mgtanθ
可知随着θ减小,F和FT都在减小,故A错误;
B.换一根更长的细线,保持θ、α不变,则F、FT都不变,故B错误;
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,根据三角形定则,如图所示
由图可知当F水平时FT最大,当FT水平时F最大,所以FT逐渐减小,F逐渐增大,故C错误;
D.根据矢量三角形作图,如图所示
可知当F方向与FT方向垂直时,F有最小值,则F先减小后增大,故D正确。
故选:D。
26.如图所示,倾角为30°的斜面顶端竖直固定一光滑的定滑轮,工人师傅用轻绳通过定滑轮牵引斜面底端的重物(可视为质点),此时连接重物的轻绳与水平面的夹角为45°,重物与斜面间的动摩擦因数μ=。在重物缓慢被牵引到斜面顶端的过程中,轻绳拉力F、重物所受摩擦力f的大小变化情况是( )
A.拉力F先减小再增大
B.拉力F逐渐减小
C.摩擦力f先减小再增大
D.摩擦力f先增大再减小
【分析】求出支持力和摩擦力的合力方向,根据矢量三角形作图,根据图中表示力的有向线段长度变化情况分析力的大小,再推导出摩擦力的计算公式分析摩擦力的变化情况。
【解答】解:对重物进行受力分析,受重力mg、斜面的支持力N、滑动摩擦力f以及拉力F,根据摩擦力的计算公式可得:f=μN,可知与N的合力F0的方向始终不变,设F0与N的夹角为α,如图1所示。
则tanα==μ=,解得:α=30°;所以F0与竖直方向的夹角为θ=30°+30°=60°。
则可认为重物在F0、mg和F的作用下处于动态平衡状态,作出一系列力的矢量三角形如图2所示,
则由图可知F先减小后增大,F0一直减小。
由于摩擦力f=F0sin30°,所以f一直减小,故BCD错误,A正确。
故选:A。
27.如图所示,一圆环套在固定的倾斜光滑杆AB上,轻绳绕过光滑定滑轮与圆环相连,整个装置处于同一竖直平面内,用力F拉动轻绳使圆环从图示位置沿杆向上缓慢运动,圆环对杆的弹力大小为FN,在圆环运动过程中,下列说法正确的是( )
A.F一直增大,FN一直减小
B.F一直增大,FN先减小后增大
C.F先减小后增大,FN一直增大
D.F先减小后增大,FN先减小后增大
【分析】做出受力分析图,圆环在F作用下缓慢上滑,处于共点力平衡状态,因此三个力构成闭合三角形,可以从图中矢量的长度确定各力大小变化。
【解答】解:对圆环受力分析如图1所示:
图1
圆环受到F、G、FN三个力的作用,三个力平衡,三个力恰组成一个闭合的三角形,由图1可知,在拉力F达到竖直方向之前,其与竖直方向夹角越来越小,则F增大,FN减小至0;
在拉力F越过竖直方向之后,支持力反向,如图2:
图2
则F仍增大,FN则反向增大,故B正确;ACD错误;
故选:B。
28.春节期间,人们挂起红灯笼,来营造一种喜庆的氛围.如图所示,轻绳a、b将灯笼悬挂于O点保持静止,绳a与水平方向的夹角为θ,绳b水平。现保持O点位置不变,b绳缓慢逆时针转动到竖直,则( )
A.轻绳a的作用力减小,轻绳b的作用力先减小后增大
B.轻绳a、b的作用力均减小
C.轻绳a、b的作用力均增大
D.轻绳a的作用力不变,轻绳b的作用力先减小后增大
【分析】选取结点O为研究对象进行受力分析,作出受力分析图,结合共点力平衡条件,三个力构成闭合三角形。确定不变的量是重力、a绳拉力方向,改变b绳方向判断各力大小变化。
【解答】解:以结点O为研究对象进行受力分析,受a、b绳的拉力以及下面绳子的拉力,下面绳子的拉力等于灯笼的重力,结点O平衡,受力分析如图所示
O点位置不变,则Ta方向不变,b绳缓慢逆时针转动到竖直过程中,由上图可知,Tb先减小后增大,Ta一直减小,BCD错误,A正确。故选:A。
29.如图所示,粗糙的水平地面上放置一物块,物块左边受到弹簧的斜向上且与水平面成θ角的拉力作用,右侧受到水平向右的拉力F作用,物块处于静止状态。若将水平向右的拉力大小变为F+ΔF,物块仍保持静止,则下列说法正确的是( )
A.弹簧的弹力一定变大
B.物块受到地面的摩擦力的大小可能不变
C.地面对物块的支持力可能变大
D.弹簧弹力和地面对物块的支持力以及拉力F的合力一定变大
【分析】弹簧的弹力与弹簧形变量有关;对物块受力分析,根据平衡条件列式分析摩擦力、支持力的变化;物块受弹簧弹力和地面对物块的支持力以及拉力F的合力与重力和摩擦力的合力平衡。
【解答】解:A、因为拉力变为F+ΔF时,物块仍处于静止状态,所以弹簧的伸长量不变,则弹簧的弹力不变,故A错误;
B、如果静摩擦力方向向右,对物块受力分析如图:
小物块在水平方向上:F+f=F弹cosθ,
即:f=F弹cosθ﹣F,
随着F的增大f逐渐减小为零,F再增大后摩擦力将反向增大,这时静摩擦力方向向左,大小可以增大到和初始摩擦力大小相等,故B正确;
C、在竖直方向上:mg=F弹sinθ+FN;
可见地面的支持力FN与拉力F无关,F弹不变化,支持力保持不变,故C错误;
D、弹簧弹力和地面对物体的支持力以及拉力F的合力,这三个力的合力与地面给物块的静摩擦力和物块的重力的合力相平衡,由B可知摩擦力大小可能不变,故摩擦力和重力的合力大小可能不变,弹簧弹力和地面对物块的支持力以及拉力F的合力大小可能不变,故D错误。
故选:B。
30.如图所示,把一重为G的物体用一水平方向的推力F=kt(k为恒量,t为时间)压在竖直的足够高的平整墙上,从t=0开始物体所受的摩擦力f随t变化的关系是图中的( )
A. B.
C. D.
【分析】由题意可知,随着时间的推移,压力不断增大,导致物体从滑动到静止。则物体所受的摩擦力先是滑动摩擦力后是静摩擦力。而滑动摩擦力的大小与推物体的压力大小成正比,而静摩擦力的大小与重力大小相等。
【解答】解:如题目中图所示,从t=0开始水平推力F=kt,即压力不断增大,则物体受到滑动摩擦力作用,所以滑动摩擦力的大小与压力正比。
因此滑动摩擦力不断增大。当物体的最大静摩擦力大于重力时,物体开始做减速运动,直到减速到零,由对称性可知,物体的加速度为g,即此时的摩擦力为2G,此时物体处于静止状态,即使推力增大,也不会影响物体的静摩擦力大小。
则有静摩擦力的大小等于重力,故C正确,ABD错误;
故选:C。
31.在中学秋季田径运动会上,高一2班李好同学奋力拼搏,勇夺男子100m冠军,下图为该同学奔跑途中的两个瞬间,用Ff1、Ff2分别表示该同学在图甲、乙两瞬间所受到的摩擦力,则关于Ff1、Ff2的方向,以下说法正确的是( )
A.Ff1向后,Ff2向后 B.Ff1向前,Ff2向前
C.Ff1向前,Ff2向后 D.Ff1向后,Ff2向前
【分析】运动员在奔跑时,后脚用力蹬,则人会向前运动,此时地面给它有个向前摩擦力。而前脚向前跨着地时,正是由于地面对它有个向后的摩擦力,才使前脚不会向前滑动。
【解答】解:当该同学奔跑途中,后脚用力向后蹬,人才向前运动,正是由于地面给后脚有个向前的静摩擦力,即Ff1向前,使运动员能向前运动;
而当前脚向前跨时,正是由于地面给前脚有个向后的静摩擦力,否则运动员会向前滑动,所以前脚受到地面的向后静摩擦力,即Ff2向后,故C正确,ABD错误。
故选:C。
32.如图所示,有一小球被轻绳拴住悬挂在天花板上并放置在斜面上,已知轻绳与竖直方向的夹角为45°,斜面倾角为37°,所有接触面都是光滑的,在斜面上施加一水平外力,使整个装置开始处于静止状态。现水平向左缓慢移动斜面,直至轻绳到达竖直位置,该过程中小球一直在斜面上,小球视为质点。下列说法正确的是( )
A.斜面开始静止时,轻绳对小球的拉力大小等于斜面对小球的支持力大小
B.斜面缓慢移动过程中,斜面对小球的支持力先增大后减小
C.斜面缓慢移动过程中,轻绳对小球的拉力一直增大
D.斜面缓慢移动过程中,斜面对水平面的压力一直不变
【分析】对小球受力分析,按力的正交分解,根据平衡条件列方程求解;然后结合角度的变化判断。
【解答】解:A、对小球受力分析,设小球受到的重力为G,将拉力T和支持力FN沿水平和竖直方向分解,如下图
水平方向上:Tsin45°=FNsin37°①
竖直方向上:Tcos45°+FNcos37°=G②
联立①②解得:FN=,T=<FN,故A错误;
BC、分析小球的受力情况,如图所示
斜面缓慢向左运动过程中,细线与竖直方向的夹角不断减小,由图可看出,拉力T逐渐增大,支持力N逐渐减小,B错误,C正确;
D、设绳子与竖直方向夹角为θ,利用整体法,竖直方向有
FN+Tcosθ=G总
由于水平向左缓慢移动斜面,θ减小且拉力T逐渐增大,可知水平面对斜面的支持力逐渐减小,由牛顿第三定律可知斜面对水平面压力减小,D错误。
故选C。
二.解答题(共3小题)
33.如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:
(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
【分析】系统原来处于平衡状态,两个弹簧均被压缩,弹簧k2的弹力等于两物体的总重力.缓慢向上提上面的木块,直到它刚离开上面弹簧时弹簧k2的弹力等于m2g,根据胡克定律分别求出下面弹簧两种状态下压缩的长度,下面木块移动的距离等于弹簧两种状态下压缩的长度之差.
【解答】解:(1)m1离开弹簧后,下面弹簧的弹力F=m2g=k2Δx,所以压缩量Δx=
(2)设下面弹簧受到的弹力为F2,压缩量为Δx2,上面弹簧受到的弹力为F1,压缩量为Δx1,
由物体的平衡及胡克定律有:F2=(m1+m2)g,
Δx2=
F1=m1g,Δx1=
所以平衡时总长为L=L1+L2﹣Δx1﹣Δx2
=L1+L2﹣﹣.
当上面的物体刚离开时总长为L′=L1+L2﹣Δx=L1+L2﹣
所以上面物体移动的距离ΔL=L′﹣L=+﹣=
答:(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
34.如图所示,质量为m1的物体A压在放于地面上的竖直轻弹簧k1上,上端与轻弹簧k2相连,轻弹簧k2上端与质量为m2物体B相连,物体B通过轻绳跨过光滑的定滑轮与轻质小桶P相连,A、B均静止.现缓慢地向小桶P内加入细砂,当弹簧k1恰好恢复原长时,(小桶一直未落地)求
(1)小桶P内所加入的细砂质量;
(2)小桶在此过程中下降的距离.
【分析】(1)当弹簧k1恰好恢复原长时,对AB组成的整体,由平衡条件求出绳子的拉力,从而求得小桶P内所加人的细砂质量.
(2)先研究开始时弹簧k1的压缩量和弹簧k2的压缩量,再研究k1恢复原长时弹簧k2的伸长量,由几何关系得到小桶在此过程中下降的距离.
【解答】解:(1)当k1恢复原长时,对AB整体分析,绳子的拉力为 F=(m1+m2) g,即小桶中细砂的质量为m1+m2.
(2)开始时,对AB分析,k1x1=(m1+m2)g,弹簧k1的压缩量为:
x1=
对B分析,k2x2=m2g,弹簧k2的压缩量为:
x2=
当k1恢复原长时,对A分析,k2x2′=m1g,弹簧k2的伸长量为:
x2′=
在此过程中,小桶下降的距离为:
h=x1+x2+x2′=(m1+m2)g
答:(1)小桶P内所加入的细砂质量是m1+m2;
(2)小桶在此过程中下降的距离是(m1+m2)g.
35.如图所示,一劲度系数为k1的弹簧,竖直地固定在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计。要使下面弹簧的弹力减为原来的时,应将上面弹簧的上端A竖直向上提高多少?
【分析】对物体受力分析,有平衡条件可求弹簧的形变量,上面弹簧的上端A竖直向上提高的距离为两弹簧的形变量之和。
【解答】解:若下面弹簧处于压缩状态,则下面弹簧弹力的变化量为mg,
根据k== 知,下面弹簧的形变量的变化量为:Δx1=,
对物体分析有:上面弹簧的弹力为:F2=mg﹣mg=mg,
则上面弹簧形变量为:Δx2==,
则有:d=Δx1+Δx2=mg()。
若下面弹簧处于伸长状态,则下面弹簧弹力的变化量为 mg,
则下面弹簧形变量的变化量Δx1=,
对物体分析有:上面弹簧的弹力F2=mg+mg=mg,
则上面弹簧的Δx2==,
则d=Δx1+Δx2=mg(+ )。
答:应将上面弹簧的上端A竖直向上提高mg()或mg(+ )。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
受力分析-中等难度
一.选择题(共32小题)
1.晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,A、B两点等高,无风状态下衣服保持静止。某一时刻衣服受到水平向右的恒定风力而发生滑动,并在新的位置保持静止,如图所示。两杆间的距离为d,绳长为,衣服和衣架的总质量为m,重力加速度为g,不计绳子的质量及绳与衣架挂钩间的摩擦,sin37°=0.6。则( )
A.相比无风时,在有风的情况下∠AOB更小
B.无风时,轻绳的拉力大小为
C.衣服在新的平衡位置时,挂钩左、右两侧绳子的拉力大小不相等
D.相比于无风时,绳子拉力在有风的情况下不变
2.如图所示,粗糙水平地面上放有横截面为圆的柱状物体A,A与墙面之间放有表面光滑的圆柱形物体B,A、B均保持静止。若将A向左移动少许,下列说法正确的是( )
A.地面对A的支持力不变
B.地面对A的摩擦力不变
C.墙对B的作用力不变
D.B对A的支持力不变
3.某兴趣小组想要运用所学力学知识进行实践研究,他们找到起重吊车的结构图,画出简化结构如图所示,AB是固定杆不可转动,B端有一光滑定滑轮;轻杆CD可绕C端自由转动,D端系着两条轻绳,一条轻绳跨过B端定滑轮连接质量为m的重物,另一轻绳缠绕在电动机转轴O上,通过电动机的牵引控制CD杆的转动从而控制重物的起落。图中所示位置两杆处于同一竖直面内,OD绳沿竖直方向,γ=30°,θ=90°,重力加速度大小为g,则( )
A.AB杆受到绳子的作用力大小为mg,方向不一定沿AB杆
B.CD杆受到绳子的作用力大小为,方向一定沿CD杆
C.当启动电动机使重物缓慢上升时,AB杆受到绳子的作用力将逐渐增大
D.当启动电动机使重物缓慢下降时,AB杆受到绳子的作用力将逐渐减小
4.如图所示,A、B、C三个物体的质量满足mA=mB=mC=m,A、B两物体通过绳子绕过定滑轮相连,B、C用劲度系数为k2的弹簧相连,劲度系数为k1的弹簧一端固定在天花板上,另一端与滑轮相连.开始时,A、B两物体在同一水平面上,不计滑轮、绳子、弹簧的重力和一切摩擦,重力加速度为g。现用竖直向下的力缓慢拉动A物体,在拉动过程中,弹簧及与A、B相连的绳子都始终竖直,到C物体刚要离开地面(A没落地,B没有与滑轮相碰),此时A、B两物体的高度差为( )
A.+ B.+
C.+ D.+
5.一个表面光滑的半圆柱体固定于墙壁上,O点为截面圆心,球体上B点有一个可视为质点的小球,通过细线连接在墙壁上的A点,下列说法正确的是( )
A.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力增加
B.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力减小
C.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力增加
D.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力减小
6.如图所示,在竖直放置的穹形支架上,一根长度不变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G。现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高)。则在此过程中绳中拉力大小( )
A.先变大后不变 B.先变大后变小
C.先变小后不变 D.先变小后变大
7.明朝谢肇的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之。”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身,假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,则木楔两侧产生推力N的大小为( )
A. B. C. D.
8.如图所示,一个内表面光滑半球形的碗放在桌面上,碗口水平,O是球心,碗的球半径为R,一根轻质杆的两端固定有A、B两个小球(可视为质点),质量分别是m1、m2,已知杆长为,杆静止时与水平面夹角为15°,则A、B两小球的质量之比是( )
A.2:1 B. C. D.
9.两个力F1和F2间的夹角为θ(0°<θ<180°),两力的合力为F,下列说法正确的是( )
A.合力F一定比分力F1和F2都大
B.若F1和F2大小不变,θ角越小,合力F越大
C.若合力F增大,θ角不变,分力F1和F2一定都增大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就增大
10.炎热的夏天,用手拧常温的碳酸饮料瓶盖时,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为( )
A.减小了瓶盖与瓶口接触面的粗糙程度
B.减小了瓶盖与瓶口螺纹间的压力
C.减小了瓶盖与瓶口接触面的接触面积
D.增大了手与瓶盖间的静摩擦力
11.如图所示,有一个小朋友,把两个半圆柱玩具甲、乙相接触并静置于水平地面上,其上有一光滑圆柱玩具丙,三者半径相同。现用水平向左的力拉甲,使甲缓慢向左移动,直至丙恰好降到地面,整个过程中乙保持静止。已知甲和乙的质量分别为3m和8m,与地面间的动摩擦因数均相同,丙的质量为4m,设最大静摩擦力等于滑动摩擦力,重力加速度为g。则下列判断正确的是( )
A.没有加拉力时,甲与地面间的摩擦力大小为2mg
B.没有加拉力时,甲对地面的压力大小为3mg
C.甲与地面间的动摩擦因数可能为0.3
D.甲与地面间的动摩擦因数可能为0.4
12.如图,倾角为θ的斜面固定在墙角,质量为M的尖劈放置在斜面上,尖劈的右侧面竖直,用轻绳系住一个质量为m的球紧靠在尖劈的右侧,轻绳与斜面平行,球与尖劈的接触面光滑,斜面对尖劈的静摩擦力恰好为0,整个系统处于静止状态。沿球心O对球施加一个水平向左的恒定推力F,系统仍处于静止状态。则( )
A.对球施加水平推力后,轻绳的拉力可能变大
B.对球施加水平推力后,尖劈对斜面的压力一定变大
C.尖劈的质量M与球的质量m之比为tan2θ
D.对球施加水平推力后,斜面对尖劈的摩擦力可能仍为0
13.一条两端固定的粗细和质量分布均匀、柔软、不可伸长的链条,在重力的作用下所具有的曲线形状,称之为悬链线.为探究其特点,现搭建如图所示的一条悬链线,经测量知两悬点A、B处切线与竖直方向夹角分别为30°和60°,两切线的交点为C,E是C点正上方链条上的点,F为悬链线的最低点,则( )
A.A、B两悬点对墙面的拉力大小之比为3:1
B.链条AF和链条FB长度之比为3:1
C.整个链条上拉力最小的点为点E
D.此时链条的重心在链条上的E点
14.如图所示,三根轻绳OA、OB、OC结于O点,OA和OB绳的另一端系于水平天花板上,OC绳C端与一重物相连,OA绳和OB绳的夹角为100°、OA绳与OC绳的夹角为120°。整个系统处于静止状态,OA绳、OB绳、OC绳上的拉力分别记为F1、F2、F3,则F1、F2、F3的大小关系正确的是( )
A.F1<F2<F3 B.F1<F3<F2 C.F2<F3<F1 D.F3<F1<F2
15.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为的小物块a相连,如图所示。质量为m的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0。从t=0时开始,对b施加沿斜面向上的拉力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。则( )
A.a、b在弹簧压缩量为处分离
B.b的加速度为
C.作用于b上的最小拉力为2mgsinθ
D.a在匀加速运动的时间为
16.如图所示,质量均为m的n(n>3)个相同匀质圆柱体依次搁置在倾角为30°的光滑斜面上,斜面底端有一竖直光滑挡板挡住使圆柱体均处于静止状态,已知重力加速度为g,则下列说法中正确的是( )
A.挡板对圆柱体1的弹力大小为
B.圆柱体1对斜面的压力大小为
C.圆柱体2对圆柱体1的压力大小为
D.若将挡板绕下端点缓慢逆时针转动60°,则转动过程中斜面对每个圆柱体的支持力均减小
17.某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.6m,b=0.1m,则物体D所受压力的大小与力F的比值为( )
A.3 B.4 C.5 D.6
18.如图所示,衣服悬挂在不可伸长的轻绳上,衣架的挂钩是光滑的,轻绳的两端固定在两根竖直杆上的A、B两点,衣服受到恒定水平向右的风力处于静止状态。保持A端位置不变,将B端分别移动到B1、B2两点。下列说法正确的是( )
A.B端移到B1,绳子张力变大
B.B端移到B1,绳子张力变小
C.B端移到B2,绳子张力变大
D.B端移到B2,绳子张力不变
19.一辆货车运载着完全相同的圆柱形光滑的空油桶,在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一个质量为m的桶C,自由地摆放在桶A、B之间。若桶A、桶B和汽车一起沿水平地面做匀速直线运动,如图所示。重力加速度大小为g,则桶A对桶C的支持力大小为( )
A.mg B.mg C.mg D.mg
20.在修建乡村住房时,工人用上了简易机械如图所示,甲站在地面上通过支架上的定滑轮拉着OA绳把建筑材料缓慢提升到楼顶后,乙再在楼顶水平拉着OB绳把建筑材料缓慢移到楼顶平台上,在乙缓慢移动建筑材料的过程中,下列说法正确的是( )
A.地面对甲的支持力变小
B.地面对甲的摩擦力变小
C.楼层对乙的作用力保持不变
D.OA绳子上的拉力先增大后减小
21.如图所示,用一轻绳通过定滑轮将质量为m的小球静置在光滑的半圆柱体上,小球的半径远小于半圆柱体截面的半径R,绳AB长度为L,长度为H的杆BC竖直且与半圆柱体边缘相切,OA与水平面夹角为θ,不计一切摩擦,重力加速度为g,下列表达式表示绳对小球的拉力F是( )
A.
B.
C.
D.
22.如图,质量为m的手机放置在支架斜面上,斜面与水平面的夹角为θ。重力加速度为g,手机始终保持静止状态。则( )
A.手机对支架的压力大小为mg,方向垂直于斜面向下
B.手机受到的摩擦力大小为mgsinθ,方向沿斜面向上
C.若θ增大,则支架对手机的摩擦力随之减小
D.若θ增大,则支架对手机的支持力保持不变
23.如图所示,一半圆形轨道放在粗糙的水平地面上,直径AB水平,轨道内表面及B端光滑,绕过B端的轻绳左端连接一小球,右端用水平力F拉轻绳,使小球在轻绳带动下从轨道最低点C开始沿轨道缓慢上滑到接近B端,轨道始终保持静止,则此过程中( )
A.地面受到轨道的静摩擦力变小
B.地面受到轨道的压力减小
C.小球对轨道的压力减小
D.轨道B端受到轻绳的作用力变小
24.如图所示,三根等长的光滑杆构成三角架,杆OA竖直放置。质量分别为m和2m的两小球用细线相连后,分别套在两杆上,在图示位置能保持静止。现将三角架绕A端在竖直平面内沿顺时针方向缓慢转动,直到AB杆水平。下列说法正确的是( )
A.OA杆对小球的弹力先增大后减小
B.OB杆对小球的弹力一直增大
C.转至AB杆水平时OB杆上的弹力大小为3mg
D.转至AB杆水平时绳上拉力为2mg
25.轻质细线上端悬挂于天花板上的O点,另一端接在质量为m的小球上,小球在水平向右的外力F作用下处于平衡状态,此时细线上的弹力大小为FT,细线与竖直方向的夹角为θ、与F的夹角为α,如图所示。以下判断正确的是( )
A.保持F水平,逐渐缓慢减小θ,则F、FT都逐渐增大
B.若换一根更长的细线,保持θ、α不变,F、FT可能都减小
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,则FT逐渐减小,F先增大后减小
D.保持小球位置不变,F沿逆时针方向缓慢转动直至F竖直向上,则F先减小后增大
26.如图所示,倾角为30°的斜面顶端竖直固定一光滑的定滑轮,工人师傅用轻绳通过定滑轮牵引斜面底端的重物(可视为质点),此时连接重物的轻绳与水平面的夹角为45°,重物与斜面间的动摩擦因数μ=。在重物缓慢被牵引到斜面顶端的过程中,轻绳拉力F、重物所受摩擦力f的大小变化情况是( )
A.拉力F先减小再增大
B.拉力F逐渐减小
C.摩擦力f先减小再增大
D.摩擦力f先增大再减小
27.如图所示,一圆环套在固定的倾斜光滑杆AB上,轻绳绕过光滑定滑轮与圆环相连,整个装置处于同一竖直平面内,用力F拉动轻绳使圆环从图示位置沿杆向上缓慢运动,圆环对杆的弹力大小为FN,在圆环运动过程中,下列说法正确的是( )
A.F一直增大,FN一直减小
B.F一直增大,FN先减小后增大
C.F先减小后增大,FN一直增大
D.F先减小后增大,FN先减小后增大
28.春节期间,人们挂起红灯笼,来营造一种喜庆的氛围.如图所示,轻绳a、b将灯笼悬挂于O点保持静止,绳a与水平方向的夹角为θ,绳b水平。现保持O点位置不变,b绳缓慢逆时针转动到竖直,则( )
A.轻绳a的作用力减小,轻绳b的作用力先减小后增大
B.轻绳a、b的作用力均减小
C.轻绳a、b的作用力均增大
D.轻绳a的作用力不变,轻绳b的作用力先减小后增大
29.如图所示,粗糙的水平地面上放置一物块,物块左边受到弹簧的斜向上且与水平面成θ角的拉力作用,右侧受到水平向右的拉力F作用,物块处于静止状态。若将水平向右的拉力大小变为F+ΔF,物块仍保持静止,则下列说法正确的是( )
A.弹簧的弹力一定变大
B.物块受到地面的摩擦力的大小可能不变
C.地面对物块的支持力可能变大
D.弹簧弹力和地面对物块的支持力以及拉力F的合力一定变大
30.如图所示,把一重为G的物体用一水平方向的推力F=kt(k为恒量,t为时间)压在竖直的足够高的平整墙上,从t=0开始物体所受的摩擦力f随t变化的关系是图中的( )
A. B.
C. D.
31.在中学秋季田径运动会上,高一2班李好同学奋力拼搏,勇夺男子100m冠军,下图为该同学奔跑途中的两个瞬间,用Ff1、Ff2分别表示该同学在图甲、乙两瞬间所受到的摩擦力,则关于Ff1、Ff2的方向,以下说法正确的是( )
A.Ff1向后,Ff2向后 B.Ff1向前,Ff2向前
C.Ff1向前,Ff2向后 D.Ff1向后,Ff2向前
32.如图所示,有一小球被轻绳拴住悬挂在天花板上并放置在斜面上,已知轻绳与竖直方向的夹角为45°,斜面倾角为37°,所有接触面都是光滑的,在斜面上施加一水平外力,使整个装置开始处于静止状态。现水平向左缓慢移动斜面,直至轻绳到达竖直位置,该过程中小球一直在斜面上,小球视为质点。下列说法正确的是( )
A.斜面开始静止时,轻绳对小球的拉力大小等于斜面对小球的支持力大小
B.斜面缓慢移动过程中,斜面对小球的支持力先增大后减小
C.斜面缓慢移动过程中,轻绳对小球的拉力一直增大
D.斜面缓慢移动过程中,斜面对水平面的压力一直不变
二.解答题(共3小题)
33.如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:
(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
34.如图所示,质量为m1的物体A压在放于地面上的竖直轻弹簧k1上,上端与轻弹簧k2相连,轻弹簧k2上端与质量为m2物体B相连,物体B通过轻绳跨过光滑的定滑轮与轻质小桶P相连,A、B均静止.现缓慢地向小桶P内加入细砂,当弹簧k1恰好恢复原长时,(小桶一直未落地)求
(1)小桶P内所加入的细砂质量;
(2)小桶在此过程中下降的距离.
35.如图所示,一劲度系数为k1的弹簧,竖直地固定在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计。要使下面弹簧的弹力减为原来的时,应将上面弹簧的上端A竖直向上提高多少?
受力分析-中等难度
参考答案与试题解析
一.选择题(共32小题)
1.晾晒衣服的绳子两端分别固定在两根竖直杆上的A、B两点,A、B两点等高,无风状态下衣服保持静止。某一时刻衣服受到水平向右的恒定风力而发生滑动,并在新的位置保持静止,如图所示。两杆间的距离为d,绳长为,衣服和衣架的总质量为m,重力加速度为g,不计绳子的质量及绳与衣架挂钩间的摩擦,sin37°=0.6。则( )
A.相比无风时,在有风的情况下∠AOB更小
B.无风时,轻绳的拉力大小为
C.衣服在新的平衡位置时,挂钩左、右两侧绳子的拉力大小不相等
D.相比于无风时,绳子拉力在有风的情况下不变
【分析】根据受力情况和几何关系,分析角度;动滑轮两端绳子的拉力总是相等;根据平衡条件和几何关系,分析F。
【解答】解:A.设无风时绳子夹角的一半为θ1,绳长为L,有风时绳子夹角的一半为θ2,钩子两边细绳与竖直方向夹角相等,则有风时如图
则有:L1+L2=Lsinθ2;d=Lsinθ1
又因为:d>L1+L2
所以:θ1>θ2
故A正确;
B.无风时,由几何关系有:
解得:θ1=37°
根据平衡条件有:mg=2Fcosθ1
解得轻绳的拉力大小:
故B错误;
C.不计绳子的质量及绳与衣架挂钩间的摩擦,则绳子的拉力总是相等,故C错误;
D.在有风的情况下,设重力与风力的合力F合与竖直方向的夹角为θ3,则有:
F合=
根据平衡条件有:F合=2F′cosθ2
解得轻绳的拉力大小:
与无风时的F=相比,θ1>θ2>θ3,可知相比于无风时,绳子拉力在有风的情况下不一定不变,故D错误。
故选:A。
2.如图所示,粗糙水平地面上放有横截面为圆的柱状物体A,A与墙面之间放有表面光滑的圆柱形物体B,A、B均保持静止。若将A向左移动少许,下列说法正确的是( )
A.地面对A的支持力不变
B.地面对A的摩擦力不变
C.墙对B的作用力不变
D.B对A的支持力不变
【分析】利用整体与隔离法、力的合成与分解法对本题进行求解。
【解答】如图,A的重力为GA,B的重力为GB,地面对A的支持力为F,地面对A的摩擦力为f,B对A的作用力为FBA,与水平方向的夹角为θ,A对B的作用力为FAB,与水平方向的夹角为θ,墙面对B的作用力为FB。
解:A.由整体分析可知,A、B保持静止时地面对A的支持力等于A与B的重力之和,将A向左移动少许,A、B仍将保持静止,因此地面对A的支持力不变,故A正确;
B.如图,对A进行受力分析可知f=FBAcosθ,又有FBA=FAB,且FABsinθ=GB,因此有f=GB,将A向左移动,θ增大,f减小,故B错误;
C.由整体分析可知,墙面对B的作用力等于地面对A的摩擦力,已知地面对A的摩擦力减小,故C错误;
D.B对A的作用力FBA=,θ增大,FBA减小,故D错误。
故选:A。
3.某兴趣小组想要运用所学力学知识进行实践研究,他们找到起重吊车的结构图,画出简化结构如图所示,AB是固定杆不可转动,B端有一光滑定滑轮;轻杆CD可绕C端自由转动,D端系着两条轻绳,一条轻绳跨过B端定滑轮连接质量为m的重物,另一轻绳缠绕在电动机转轴O上,通过电动机的牵引控制CD杆的转动从而控制重物的起落。图中所示位置两杆处于同一竖直面内,OD绳沿竖直方向,γ=30°,θ=90°,重力加速度大小为g,则( )
A.AB杆受到绳子的作用力大小为mg,方向不一定沿AB杆
B.CD杆受到绳子的作用力大小为,方向一定沿CD杆
C.当启动电动机使重物缓慢上升时,AB杆受到绳子的作用力将逐渐增大
D.当启动电动机使重物缓慢下降时,AB杆受到绳子的作用力将逐渐减小
【分析】绳对杆的作用力的方向是沿着绳的方向,那么将绳对杆的力分解后求合力。
【解答】解:A.杆AB固定于平台,杆力不一定沿杆,同一条绳的力大小相等,其合力一定在其角平分线上,由于杆的力不一定沿杆,如图所示
两个力T所作力的平行四边形为菱形,根据平衡条件可得
T=mg
根据几何关系可得
a+β=60°
对角线为F杆,则AB杆受到绳子的作用力大小为
F杆=2Tcos30°=mg
故A错误;
B.根据题意D端连接两条轻绳,两条轻绳的力不一定大小相等,且CD杆为铰链连接,为“活”杆,杆力沿着杆的方向,水平方向,根据
F'杆cos60°=Tcos30°=mgcos30°
解得
F'杆=mg
故B错误;
CD.当启动电动机使重物缓慢下降时,即T=mg不变,∠DBM变小,根据
F杆=2Tcos
可知F杆增大,故C正确,D错误。
故选:C。
4.如图所示,A、B、C三个物体的质量满足mA=mB=mC=m,A、B两物体通过绳子绕过定滑轮相连,B、C用劲度系数为k2的弹簧相连,劲度系数为k1的弹簧一端固定在天花板上,另一端与滑轮相连.开始时,A、B两物体在同一水平面上,不计滑轮、绳子、弹簧的重力和一切摩擦,重力加速度为g。现用竖直向下的力缓慢拉动A物体,在拉动过程中,弹簧及与A、B相连的绳子都始终竖直,到C物体刚要离开地面(A没落地,B没有与滑轮相碰),此时A、B两物体的高度差为( )
A.+ B.+
C.+ D.+
【分析】分别求出初状态两根弹簧的形变量,再求出末状态两根弹簧的形变量,根据位移关系求解A、B两物体的高度差。
【解答】解:设开始BC间弹簧的压缩量为x1,上面的弹簧伸长量为x′1,绳子拉力为T;
对物体A根据平衡条件可得:T=mg;
对B物体根据平衡条件可得:2mg=k2x1+T
解得:x1=;
对滑轮根据平衡条件可得:2T=k1x′1
解得:x′1=;
设C物体刚要离开地面时BC间弹簧的伸长量为x2,上面的弹簧伸长量为x′2,绳子拉力为T′;
对物体C根据平衡条件可得:2mg=k2x2
解得:x2=;
C物体刚要离地时,上端弹簧的拉力为T′=8mg
对滑轮根据平衡条件可得:8mg=k1x′2
解得:x′2=。
所以此过程中A下降的高度为:hA=x1+x2+2(x′2﹣x′1)=+
此过程中B物体上升的高度:hB=x1+x2=
此时A、B两物体的高度差为Δh=hA+hB=+,故D正确、ABC错误。
故选:D。
5.一个表面光滑的半圆柱体固定于墙壁上,O点为截面圆心,球体上B点有一个可视为质点的小球,通过细线连接在墙壁上的A点,下列说法正确的是( )
A.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力增加
B.若细线长度和A、O点位置不变,增加柱体半径,则小球所受支持力减小
C.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力增加
D.若细线长度和A、O点位置不变,减小柱体半径,则线上拉力减小
【分析】对小球进行受力分析,做出力的矢量三角形,根据几何三角形和力三角形相似,分析力的大小变化。
【解答】解:对小球进行受力分析,可知它受重力G,柱体给它的支持力FN,细线中拉力FT,做出力的矢量三角形如图所示
根据相似性则有
AB.增加柱体半径,即OB增加,所以小球所受的支持力增加;减小柱体半径,小球所受的支持力减小,故A正确,B错误;
CD.增加或减小柱体半径,但是细线长度AB不变,拉力不变,故CD错误。
故选:A。
6.如图所示,在竖直放置的穹形支架上,一根长度不变且不可伸长的轻绳通过轻质光滑滑轮悬挂一重物G。现将轻绳的一端固定于支架上的A点,另一端从B点沿支架缓慢地向C点靠近(C点与A点等高)。则在此过程中绳中拉力大小( )
A.先变大后不变 B.先变大后变小
C.先变小后不变 D.先变小后变大
【分析】当轻绳的右端从B点移到直杆最上端时,两绳的夹角增大.滑轮两侧绳子的拉力大小相等,方向关于竖直方向对称.以滑轮为研究对象,根据平衡条件研究绳的拉力变化情况.当轻绳的右端从直杆的最上端移到C点的过程中,根据几何知识分析得到滑轮两侧绳子的夹角不变,由平衡条件判断出绳子的拉力保持不变。
【解答】解:当轻绳的右端从B点移到直杆最上端D时,设两绳的夹角为2θ.以滑轮为研究对象,分析受力情况,作出力图如图1所示。根据平衡条件得
2Fcosθ=mg
得到绳子的拉力F=
所以在轻绳的右端从B点移到直杆最上端时D的过程中,θ增大,cosθ减小,则F变大;
当轻绳的右端从直杆最上端的D点移到C点时,设两绳的夹角为2α。
设绳子总长为L,两直杆间的距离为s,由数学知识得到
sinα=,L、S不变,则α保持不变。
再根据平衡条件可知,两绳的拉力F保持不变。
所以绳中拉力大小变化的情况是先变大后不变。故BCD错误,A正确。
故选:A。
7.明朝谢肇的《五杂组》中记载:“明姑苏虎丘寺庙倾侧,议欲正之,非万缗不可。一游僧见之,曰:无烦也,我能正之。”游僧每天将木楔从塔身倾斜一侧的砖缝间敲进去,经月余扶正了塔身,假设所用的木楔为等腰三角形,木楔的顶角为θ,现在木楔背上加一力F,方向如图所示,则木楔两侧产生推力N的大小为( )
A. B. C. D.
【分析】由于木楔处在静止状态,可将力F沿与木楔的斜面垂直且向上的方向进行分解,根据平行四边形定则,画出力F按效果分解的图示。并且可据此求出木楔两侧产生的推力,再进行分析。
【解答】解:选木楔为研究对象,木楔受到的力有:水平向左的F和两侧给它的与木楔的斜面垂直的弹力,由于木楔处于平衡状态,所以两侧给木楔的斜面垂直的弹力与F沿两侧分解的力是相等的,力F的分解如图:
则F=F1cos(90°﹣ )+F2cos(90°﹣ )=2F1cos(90°﹣)=2F1sin
N=F1
故得N=,故ABD错误,C正确。
故选:C。
8.如图所示,一个内表面光滑半球形的碗放在桌面上,碗口水平,O是球心,碗的球半径为R,一根轻质杆的两端固定有A、B两个小球(可视为质点),质量分别是m1、m2,已知杆长为,杆静止时与水平面夹角为15°,则A、B两小球的质量之比是( )
A.2:1 B. C. D.
【分析】先对两小球和杆组成的系统作为研究对象,根据受力分析解得碗对A、B的作用力,再隔离分析可知A、B两球的质量之比。
【解答】解:由几何关系可知OA、OB的夹角为90°,OB与水平方向的夹角为30°,OA与水平方向的夹角为60°,选取两小球和杆作为研究对象,受力分析如下图所示
由平衡条件得,F1在水平方向的分力F'和F2在水平方向的分力F''相等,即
F1cos60°=F2cos30°
所以
=
在以小球1为研究对象,受力分析如下图所示
根据平衡条件得F与m1g的合力与F1等大反向,图中两个阴影三角形相似,则得
再以小球2为研究对象得
则得
解得
故B正确,ACD错误。
故选:B。
9.两个力F1和F2间的夹角为θ(0°<θ<180°),两力的合力为F,下列说法正确的是( )
A.合力F一定比分力F1和F2都大
B.若F1和F2大小不变,θ角越小,合力F越大
C.若合力F增大,θ角不变,分力F1和F2一定都增大
D.如果夹角θ不变,F1大小不变,只要F2增大,合力F就增大
【分析】力是矢量,有大小、方向,遵循平行四边形定则;合力的范围:|F1﹣F2|<F合≤F1+F2,据此结合实际分析合力与分力的关系即可。
【解答】解:A:由力的合成方法可知,两力合力的范围|F1﹣F2|<F合≤F1+F2,所以合力有可能大于任一分力,也可能小于任一分力,还可能与两个分力都相等,故A错误;
B:若F1和F2大小不变,力的合成遵循平行四边形定则,θ角越小,合力F越大,故B正确;
C:如果夹角θ不变,F1大小不变,F2增大,合力F可以减小,也可以增大,故C错误;
D:如果夹角θ不变,F1大小不变,只要F2增大,合力F可以减小,也可以增大,故D错误。
故选:B。
10.炎热的夏天,用手拧常温的碳酸饮料瓶盖时,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为( )
A.减小了瓶盖与瓶口接触面的粗糙程度
B.减小了瓶盖与瓶口螺纹间的压力
C.减小了瓶盖与瓶口接触面的接触面积
D.增大了手与瓶盖间的静摩擦力
【分析】依据滑动摩擦力大小由动摩擦因数及压力有关,与接触面积无关,从而即可分析。
【解答】解:ABC、常温下的碳酸饮料对瓶盖有压力,手在水平拧塑料瓶盖的同时再向下压瓶盖能更容易将瓶盖拧开,这主要是因为减小了瓶盖与瓶口螺纹间的压力,从而减小瓶盖与瓶口的滑动摩擦力,并没有改变瓶盖与瓶口接触面的粗糙程度,同时瓶盖与瓶口的滑动摩擦力大小与接触面的接触面积大小无关,故AC错误,B正确;
D、手在水平拧塑料瓶盖的同时再向下压瓶盖,增大了手与瓶盖间的静摩擦力,但能更容易将瓶盖拧开,与其无关,故D错误;
故选:B。
11.如图所示,有一个小朋友,把两个半圆柱玩具甲、乙相接触并静置于水平地面上,其上有一光滑圆柱玩具丙,三者半径相同。现用水平向左的力拉甲,使甲缓慢向左移动,直至丙恰好降到地面,整个过程中乙保持静止。已知甲和乙的质量分别为3m和8m,与地面间的动摩擦因数均相同,丙的质量为4m,设最大静摩擦力等于滑动摩擦力,重力加速度为g。则下列判断正确的是( )
A.没有加拉力时,甲与地面间的摩擦力大小为2mg
B.没有加拉力时,甲对地面的压力大小为3mg
C.甲与地面间的动摩擦因数可能为0.3
D.甲与地面间的动摩擦因数可能为0.4
【分析】根据对称性画出受力分析图,根据共点力的平衡条件求解甲与地面摩擦力,结合牛顿第三定律解得压力;先求出没有拉力时甲、乙两半圆柱体半径中心之间的距离,丙恰好降到地面时,求出此时甲半圆柱体半径重心与丙圆柱体中心连线与地面夹角为θ,根据共点力平衡条件分析动摩擦因数的范围,从而分析CD。
【解答】解:AB.对丙受力分析,如图1所示
图1
根据共点力平衡条件结合几何关系可知弹力和竖直方向的夹角θ=30°,故
地面对甲的摩擦力大小为f,对甲受力分析,如图2所示
图2
根据共点力平衡,水平方向上
f=Fsinθ
解得
在竖直方向上
故AB错误;
CD.丙恰好降到地面时,甲和乙与丙之间的相互作用力最大为Fm,甲和乙恰好不相对地面滑动,对丙受力分析,如图3所示
图3
由几何关系可知Fm 与竖直方向的夹角α=60°,根据共点力平衡,可得
2Fmcos60°=4mg
解得
Fm=4mg
对乙受力分析如图4所示
图4
最大静摩擦力至少为
竖直方向上
N=8mg+F′msin30°=10mg
根据摩擦力公式有
fmax=μminN
解得
故C错误,D正确。
故选:D。
12.如图,倾角为θ的斜面固定在墙角,质量为M的尖劈放置在斜面上,尖劈的右侧面竖直,用轻绳系住一个质量为m的球紧靠在尖劈的右侧,轻绳与斜面平行,球与尖劈的接触面光滑,斜面对尖劈的静摩擦力恰好为0,整个系统处于静止状态。沿球心O对球施加一个水平向左的恒定推力F,系统仍处于静止状态。则( )
A.对球施加水平推力后,轻绳的拉力可能变大
B.对球施加水平推力后,尖劈对斜面的压力一定变大
C.尖劈的质量M与球的质量m之比为tan2θ
D.对球施加水平推力后,斜面对尖劈的摩擦力可能仍为0
【分析】以尖劈和球整体为研究对象,再以球为研究对象,根据共点力平衡条件分析尖劈和小球的质量关系,对球施加推力后,再对整体分析斜面对尖劈的摩擦力和尖劈对斜面的压力的变化。
【解答】解:C.对球施加水平推力前,以尖劈和球整体为研究对象,如图1,可知轻绳的拉力
T=(M+m )gsinθ
斜面对尖劈的支持力
N1=(M+m)gcosθ
以球为研究对象,如图2,可知轻绳的拉力
T=
联立解得
=
故C错误。
A.以球为研究对象,可知对球施加水平推力后不影响竖直方向力的大小,轻绳的拉力不变,如图3,故A错误;
BD.以尖劈和球整体为研究对象,对球施加水平推后,如图4,有
N'1=(M+m)gcosθ+Fsinθ
总重力不变,可得斜面对尖劈的弹力变大,即尖劈对斜面的压力变大;轻绳拉力T不变,总重力不变,施加推力F后,要保持平衡,有
T+Fcosθ=(M+m)gsinθ+f
则斜面对尖劈的摩擦力沿斜面向下,斜面对尖劈的摩擦力不可能为0,故B正确,D错误。
故选:B。
13.一条两端固定的粗细和质量分布均匀、柔软、不可伸长的链条,在重力的作用下所具有的曲线形状,称之为悬链线.为探究其特点,现搭建如图所示的一条悬链线,经测量知两悬点A、B处切线与竖直方向夹角分别为30°和60°,两切线的交点为C,E是C点正上方链条上的点,F为悬链线的最低点,则( )
A.A、B两悬点对墙面的拉力大小之比为3:1
B.链条AF和链条FB长度之比为3:1
C.整个链条上拉力最小的点为点E
D.此时链条的重心在链条上的E点
【分析】根据“三力汇交”原理对悬链线受力分析,再根据共点力的平衡条件分析求解两悬点处墙壁对链条的拉力大小之比,根据牛顿第三定律求解链条对墙面的拉力大小之比;对两部分链条进行受力分析,根据平衡条件求解两部分链条的质量之比,再求长度之比;在链条上任取一点D(除F外),取D与F点之间这一部分链条为对象,根据平衡条件分析作答;根据“三力汇交”原理可知E点在重力作用线上,再根据链条的形状分析重心的位置。
【解答】解:A.对悬链线受力分析,两悬点A、B处切线与竖直方向夹角分别为30°和60°,受力分析图如图1所示:
根据平衡条件TA=mgcos30°
TB=mgcos60°
代入数据联立解得,A、B两悬点处墙壁对链条的拉力大小之比为:1
根据牛顿第三定律,A、B两悬点链条对墙面的拉力大小之比:1,故A错误;
B.设最低点F处的张力为T,左侧悬链质量为m1,右侧质量为m2,两部分链条的受力图如图2所示:
根据平衡条件,对左侧悬链m1g=
对右侧悬链m2g=
得两部分链条的质量之比=3
链条AF和链条FB长度之比为3:1,故B正确;
C.在链条上任取一点D(除F外),取D与F点之间这一部分链条为对象,质量为Δm,D点的张力为TD
由于F点的张力处于水平方向,根据平衡条件结合数学知识TD=>T
可知整个链条上拉力最小的点为最低点F,故C错误;
D.根据“三力汇交”原理,由题意可知,重力作用线经过E点,但由于链条形状不规则,重心不在链条的E点,故D错误。
故选:B。
14.如图所示,三根轻绳OA、OB、OC结于O点,OA和OB绳的另一端系于水平天花板上,OC绳C端与一重物相连,OA绳和OB绳的夹角为100°、OA绳与OC绳的夹角为120°。整个系统处于静止状态,OA绳、OB绳、OC绳上的拉力分别记为F1、F2、F3,则F1、F2、F3的大小关系正确的是( )
A.F1<F2<F3 B.F1<F3<F2 C.F2<F3<F1 D.F3<F1<F2
【分析】结点O受力平衡,做出O点受力分析图,结合正弦定理即可求解。
【解答】解:对节点O进行受力分析如图所示
根据正弦定理
可知 F1<F2<F3,故A正确,BCD错误。
故选:A。
15.一轻弹簧的一端固定在倾角为θ的固定光滑斜面的底部,另一端和质量为的小物块a相连,如图所示。质量为m的小物块b紧靠a静止在斜面上,此时弹簧的压缩量为x0。从t=0时开始,对b施加沿斜面向上的拉力,使b始终做匀加速直线运动。经过一段时间后,物块a、b分离;再经过同样长的时间,b距其出发点的距离恰好也为x0。弹簧的形变始终在弹性限度内,重力加速度大小为g。则( )
A.a、b在弹簧压缩量为处分离
B.b的加速度为
C.作用于b上的最小拉力为2mgsinθ
D.a在匀加速运动的时间为
【分析】A、根据初速为0的匀变加直线运动推论:连续相等时间间隔内位移之比1:3:5……计算分离的位置;
B、两物体刚好要分离,即a与b之间无相互作用力,对a由牛顿第二定律,求出分离时的加速度;
C、分离前对整体分析可知,由牛顿第二定律分析出刚开始运动时拉力最小,进而求出最小拉力;
D、分离前a在匀加速运动,通过位移求时间。
【解答】解:A、由于初速度为0,b在分离前位移x1和分离后相等时间内位移x2之比为:
且由题可知:x1+x2=x0
解得:
初始时压缩量为x0,分离前位移,即压缩量减小,可得a、b在弹簧压缩量为时分离,故A错误;
B、两物体刚好要分离时a与b之间无相互作用力,对a由牛顿第二定律可得
初始时小物体b紧靠a静止在斜面上,将二者看成一个整体,可知弹力大小与整体重力的分力大小相等,有
kx0=(+m)gsinθ
解得:a=gsinθ,故B错误;
C、分离前对整体分析可知,由牛顿第二定律有
则刚开始运动时拉力最小,则Δx=x0,且
可得:,故C错误;
D、a与b在b向上运动的位移刚好分离,此前a在匀加速运动,则有:
解得:,故D正确。
故选:D。
16.如图所示,质量均为m的n(n>3)个相同匀质圆柱体依次搁置在倾角为30°的光滑斜面上,斜面底端有一竖直光滑挡板挡住使圆柱体均处于静止状态,已知重力加速度为g,则下列说法中正确的是( )
A.挡板对圆柱体1的弹力大小为
B.圆柱体1对斜面的压力大小为
C.圆柱体2对圆柱体1的压力大小为
D.若将挡板绕下端点缓慢逆时针转动60°,则转动过程中斜面对每个圆柱体的支持力均减小
【分析】小球对挡板和对斜面的压力不好求,我们可以求挡板和斜面对小球的支持力,利用牛顿第三定律求解这两个力,小球静止,对小球受力分析后应用平衡条件列式求解。
【解答】解:A、以整体为研究对象,受力情况如图所示:
挡板对圆柱体1的弹力大小为T=nmgtan30°=,故A错误;
B、以圆柱体1为研究对象,受力如图,则:
沿斜面的方向:N′+mgsin30°=N2cos30°
垂直于斜面的方向:N1=N2sin30°+mgcos30°
所以N1=.根据牛顿第三定律可得圆柱体1对斜面的压力大小为,故B正确;
C、选取除1以外的所有圆柱体为研究对象,整体受到重力、斜面从支持力和圆柱体1的支持力,根据共点力平衡的条件可知,整体受到的1的支持力与整体的重力沿斜面方向的分力大小相等,方向相反,所以:N21=(n﹣1)mgsin30°=mg,根据牛顿第三定律可得,圆柱体2对圆柱体1的压力大小为mg,故C错误;
D、若将挡板绕下端点缓慢逆时针转动60°,圆柱体2到圆柱体n受力情况不变,则转动过程中斜面对2到n圆柱体的支持力均不变,故D错误。
故选:B。
17.某压榨机的结构示意图如图所示,其中B为固定铰链,若在A铰链处作用一垂直于墙壁的力F,则由于力F的作用,使滑块C压紧物体D,设C与D光滑接触,杆的重力及滑块C的重力不计,图中a=0.6m,b=0.1m,则物体D所受压力的大小与力F的比值为( )
A.3 B.4 C.5 D.6
【分析】根据力F的作用效果将它分解,再将AC所受压力的作用效果进行分解,根据数学知识求出物体D所受压力的大小是F的多少倍。
【解答】解:设力F与水平方向的夹角为θ,将力F按作用效果沿AB和AC两个方向进行分解,作出力的分解图如图甲所示。则有:
2F1cosθ=F
则得 F1=F2= 再将F2按作用效果分解为FN和FN′,作出力的分解图如图乙所示。
则有:
FN=F2sinθ
联立得到:FN=
根据几何知识得可知tanθ==6;
得到:FN=3F,故A正确,BCD错误;
故选:A。
18.如图所示,衣服悬挂在不可伸长的轻绳上,衣架的挂钩是光滑的,轻绳的两端固定在两根竖直杆上的A、B两点,衣服受到恒定水平向右的风力处于静止状态。保持A端位置不变,将B端分别移动到B1、B2两点。下列说法正确的是( )
A.B端移到B1,绳子张力变大
B.B端移到B1,绳子张力变小
C.B端移到B2,绳子张力变大
D.B端移到B2,绳子张力不变
【分析】对挂钩受力分析,根据平衡条件结合几何关系列式求解;注意确定悬点从B上移或下移,细线与杆的夹角的变化。
【解答】解:对挂钩受力分析,如图所示,将重力G与风力F合成为等效重力G′,两段绳的拉力T等大,其合力与等效重力G′等大反向。
过A、B分别做平行于G′的直线a、b(直线a、b为等效的晾衣杆),直线a、b之间的距离为c,设绳子与直线a、b的夹角为θ。
由几何关系和平衡条件可得:2Tcosθ=G′
将B端移动到B1点,相当于将直线b平移到直线b1,即直线a、b之间的距离变大(等效的晾衣杆距离变大),绳子总长度一定,由几何关系可知,θ较变大,cosθ变小,则T增大。
同理,将B端移动到B2点,相当于将直线b平移到直线b2,即直线a、b之间的距离变小(等效的晾衣杆距离变小),绳子总长度一定,由几何关系可知,θ较变小,cosθ变大,则T减小。
故A正确,BCD错误。
故选:A。
19.一辆货车运载着完全相同的圆柱形光滑的空油桶,在车厢底,一层油桶平整排列,相互紧贴并被牢牢固定,上一层只有一个质量为m的桶C,自由地摆放在桶A、B之间。若桶A、桶B和汽车一起沿水平地面做匀速直线运动,如图所示。重力加速度大小为g,则桶A对桶C的支持力大小为( )
A.mg B.mg C.mg D.mg
【分析】对球C进行受力分析,根据共点力平衡、力的合成以及数学知识解决问题
【解答】解:对物体C受力分析,受重力、A和B对C的弹力
根据几何知识:弹力与竖直方向的夹角为30°
根据平衡条件得到:
,故ACD错误,B正确。
故选:B。
20.在修建乡村住房时,工人用上了简易机械如图所示,甲站在地面上通过支架上的定滑轮拉着OA绳把建筑材料缓慢提升到楼顶后,乙再在楼顶水平拉着OB绳把建筑材料缓慢移到楼顶平台上,在乙缓慢移动建筑材料的过程中,下列说法正确的是( )
A.地面对甲的支持力变小
B.地面对甲的摩擦力变小
C.楼层对乙的作用力保持不变
D.OA绳子上的拉力先增大后减小
【分析】根据受力平衡分析乙移动建筑材料的过程中,可知滑轮与乙这一侧绳子OC与竖直方向的夹角θ逐渐变大,根据平衡条件分析拉力的变化,对甲根据共点力平衡条件分析,甲与地面的摩擦力、支持力的变化,对乙,根据力的合成分析楼层对乙的作用力。
【解答】解:D.设建筑材料的重力为G,OA绳对建筑材料的拉力为FOA,乙对OB绳的拉力大小为FOB,如图1
图1
根据平衡条件有FOA=
θ增大,则FOA增大,故D错误;
B.对甲受力分析,由平衡条件可知,甲与地面之间的摩擦力大小等于OA绳对甲的拉力在水平方上的分力,由于OA绳对甲的拉力逐渐增大且OA绳与水平方向夹角不变,所以可得甲与地面之间的摩擦力逐渐增大,故B错误;
A.对甲受力分析,竖直方向由平衡条件可知,N+FOAsinα=m甲g,可知地面对甲的支持力变小,故A正确;
C.对乙受力分析,如图2
图2
乙受到的支持力与自身重力大小相等,摩擦力与OB绳上的拉力大小相等,由于OB绳上的拉力变大,所以摩擦力变大,摩擦力与支持力的合力变大,由平行四边定则合力方向变化,则楼层对乙的作用力方向变化,大小变大,故C错误。
故选:A。
21.如图所示,用一轻绳通过定滑轮将质量为m的小球静置在光滑的半圆柱体上,小球的半径远小于半圆柱体截面的半径R,绳AB长度为L,长度为H的杆BC竖直且与半圆柱体边缘相切,OA与水平面夹角为θ,不计一切摩擦,重力加速度为g,下列表达式表示绳对小球的拉力F是( )
A.
B.
C.
D.
【分析】对小球受力分析,根据力的矢量三角形与几何三角形的相似性解答。
【解答】解:对小球受力分析,受重力、支持力和拉力,如图所示
根据相似性有:
=
解得
F=
故C正确,ABD错误;
故选:C。
22.如图,质量为m的手机放置在支架斜面上,斜面与水平面的夹角为θ。重力加速度为g,手机始终保持静止状态。则( )
A.手机对支架的压力大小为mg,方向垂直于斜面向下
B.手机受到的摩擦力大小为mgsinθ,方向沿斜面向上
C.若θ增大,则支架对手机的摩擦力随之减小
D.若θ增大,则支架对手机的支持力保持不变
【分析】对手机受力分析,根据平衡条件列式求解手机所受支持力和摩擦力,判断其随θ的变化;支架对手机的作用力与重力等大反向。
【解答】解:AB.手机处于静止状态,对手机受力分析,设手机受到的支持力为N,摩擦力为f
根据共点力平衡条件有
N=mgcosθ
f=mgsinθ
根据牛顿第三定律可知手机对支架的压力大小与手机受到的支持力大小相等,为mgcosθ,方向垂直于斜面向下。手机受到的摩擦力大小为mgsinθ,方向沿斜面向上,故A错误,B正确;
CD.若θ增大,sinθ增大,cosθ减小,则支架对手机的摩擦力随之增大,支架对手机的支持力减小,故CD错误;
故选:B。
23.如图所示,一半圆形轨道放在粗糙的水平地面上,直径AB水平,轨道内表面及B端光滑,绕过B端的轻绳左端连接一小球,右端用水平力F拉轻绳,使小球在轻绳带动下从轨道最低点C开始沿轨道缓慢上滑到接近B端,轨道始终保持静止,则此过程中( )
A.地面受到轨道的静摩擦力变小
B.地面受到轨道的压力减小
C.小球对轨道的压力减小
D.轨道B端受到轻绳的作用力变小
【分析】对整体受力分析可知地面受轨道压力的变化情况,对小球受力分析,根据正弦定理与几何关系可分析ACD项。
【解答】解:B.对小球、轨道整体,由受力平衡知地面对轨道的静摩擦力大小为f=F,地面对轨道的支持力N1与小球和轨道的总重力平衡,即N1不变,根据牛顿第三定律知地面受到轨道的压力不变,故B错误;
AC.小球受力情况如图所示:
设轨道对小球的支持力大小为N2,与竖直方向夹角为θ,轻绳与竖直方向夹角为α,有
﹣θ+2 (θ+α)=π
即θ=﹣2α
根据正弦定理有
==
可得
N2=mgtanα
F=mg=mg (2cosα﹣)
α从45°逐渐减小,则N2将减小,F将增大,地面受到轨道的静摩擦力变大,故A错误,C正确;
D.由于B端两侧轻绳的夹角减小且F增大,轨道B端受到轻绳的作用力增大,故D错误。
故选:C。
24.如图所示,三根等长的光滑杆构成三角架,杆OA竖直放置。质量分别为m和2m的两小球用细线相连后,分别套在两杆上,在图示位置能保持静止。现将三角架绕A端在竖直平面内沿顺时针方向缓慢转动,直到AB杆水平。下列说法正确的是( )
A.OA杆对小球的弹力先增大后减小
B.OB杆对小球的弹力一直增大
C.转至AB杆水平时OB杆上的弹力大小为3mg
D.转至AB杆水平时绳上拉力为2mg
【分析】根据整体分析法画力的矢量三角形,结合几何关系分析杆对小球的弹力变化,根据几何关系解得CD项。
【解答】解:AB.将两小球看成一个整体,构建整体受力的矢量三角形,如图1所示:
图1
两弹力间的夹角大小不变,整体重力大小方向均不变,可构造该矢量三角形的外接圆,在OA杆对小球的弹力方向由水平变化的过程中,OA杆对小球的弹力逐渐增大,OB杆对小球的弹力一直减小。故AB错误;
CD.末状态时,N1、N2间的夹角为120°,N1、N2与竖直方向的夹角均为60°,如图2
图2
根据合成规律可知末态时两杆对球的弹力大小相等,均为3mg。
以OA杆上的小球为研究对象,根据余弦定理
cos60°=
可得细绳对小球的作用力
T=mg
故C正确,D错误。
故选:C。
25.轻质细线上端悬挂于天花板上的O点,另一端接在质量为m的小球上,小球在水平向右的外力F作用下处于平衡状态,此时细线上的弹力大小为FT,细线与竖直方向的夹角为θ、与F的夹角为α,如图所示。以下判断正确的是( )
A.保持F水平,逐渐缓慢减小θ,则F、FT都逐渐增大
B.若换一根更长的细线,保持θ、α不变,F、FT可能都减小
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,则FT逐渐减小,F先增大后减小
D.保持小球位置不变,F沿逆时针方向缓慢转动直至F竖直向上,则F先减小后增大
【分析】根据共点力平衡条件列式分析F、FT的大小变化,绳长对力的大小无影响,根据力的矢量合成图分析CD项。
【解答】解:A.保持F水平,逐渐缓慢减小θ,对小球受力分析有FTcosθ=mg,F=mgtanθ
可知随着θ减小,F和FT都在减小,故A错误;
B.换一根更长的细线,保持θ、α不变,则F、FT都不变,故B错误;
C.保持α不变,逐渐缓慢增大θ,直至悬线水平,根据三角形定则,如图所示
由图可知当F水平时FT最大,当FT水平时F最大,所以FT逐渐减小,F逐渐增大,故C错误;
D.根据矢量三角形作图,如图所示
可知当F方向与FT方向垂直时,F有最小值,则F先减小后增大,故D正确。
故选:D。
26.如图所示,倾角为30°的斜面顶端竖直固定一光滑的定滑轮,工人师傅用轻绳通过定滑轮牵引斜面底端的重物(可视为质点),此时连接重物的轻绳与水平面的夹角为45°,重物与斜面间的动摩擦因数μ=。在重物缓慢被牵引到斜面顶端的过程中,轻绳拉力F、重物所受摩擦力f的大小变化情况是( )
A.拉力F先减小再增大
B.拉力F逐渐减小
C.摩擦力f先减小再增大
D.摩擦力f先增大再减小
【分析】求出支持力和摩擦力的合力方向,根据矢量三角形作图,根据图中表示力的有向线段长度变化情况分析力的大小,再推导出摩擦力的计算公式分析摩擦力的变化情况。
【解答】解:对重物进行受力分析,受重力mg、斜面的支持力N、滑动摩擦力f以及拉力F,根据摩擦力的计算公式可得:f=μN,可知与N的合力F0的方向始终不变,设F0与N的夹角为α,如图1所示。
则tanα==μ=,解得:α=30°;所以F0与竖直方向的夹角为θ=30°+30°=60°。
则可认为重物在F0、mg和F的作用下处于动态平衡状态,作出一系列力的矢量三角形如图2所示,
则由图可知F先减小后增大,F0一直减小。
由于摩擦力f=F0sin30°,所以f一直减小,故BCD错误,A正确。
故选:A。
27.如图所示,一圆环套在固定的倾斜光滑杆AB上,轻绳绕过光滑定滑轮与圆环相连,整个装置处于同一竖直平面内,用力F拉动轻绳使圆环从图示位置沿杆向上缓慢运动,圆环对杆的弹力大小为FN,在圆环运动过程中,下列说法正确的是( )
A.F一直增大,FN一直减小
B.F一直增大,FN先减小后增大
C.F先减小后增大,FN一直增大
D.F先减小后增大,FN先减小后增大
【分析】做出受力分析图,圆环在F作用下缓慢上滑,处于共点力平衡状态,因此三个力构成闭合三角形,可以从图中矢量的长度确定各力大小变化。
【解答】解:对圆环受力分析如图1所示:
图1
圆环受到F、G、FN三个力的作用,三个力平衡,三个力恰组成一个闭合的三角形,由图1可知,在拉力F达到竖直方向之前,其与竖直方向夹角越来越小,则F增大,FN减小至0;
在拉力F越过竖直方向之后,支持力反向,如图2:
图2
则F仍增大,FN则反向增大,故B正确;ACD错误;
故选:B。
28.春节期间,人们挂起红灯笼,来营造一种喜庆的氛围.如图所示,轻绳a、b将灯笼悬挂于O点保持静止,绳a与水平方向的夹角为θ,绳b水平。现保持O点位置不变,b绳缓慢逆时针转动到竖直,则( )
A.轻绳a的作用力减小,轻绳b的作用力先减小后增大
B.轻绳a、b的作用力均减小
C.轻绳a、b的作用力均增大
D.轻绳a的作用力不变,轻绳b的作用力先减小后增大
【分析】选取结点O为研究对象进行受力分析,作出受力分析图,结合共点力平衡条件,三个力构成闭合三角形。确定不变的量是重力、a绳拉力方向,改变b绳方向判断各力大小变化。
【解答】解:以结点O为研究对象进行受力分析,受a、b绳的拉力以及下面绳子的拉力,下面绳子的拉力等于灯笼的重力,结点O平衡,受力分析如图所示
O点位置不变,则Ta方向不变,b绳缓慢逆时针转动到竖直过程中,由上图可知,Tb先减小后增大,Ta一直减小,BCD错误,A正确。故选:A。
29.如图所示,粗糙的水平地面上放置一物块,物块左边受到弹簧的斜向上且与水平面成θ角的拉力作用,右侧受到水平向右的拉力F作用,物块处于静止状态。若将水平向右的拉力大小变为F+ΔF,物块仍保持静止,则下列说法正确的是( )
A.弹簧的弹力一定变大
B.物块受到地面的摩擦力的大小可能不变
C.地面对物块的支持力可能变大
D.弹簧弹力和地面对物块的支持力以及拉力F的合力一定变大
【分析】弹簧的弹力与弹簧形变量有关;对物块受力分析,根据平衡条件列式分析摩擦力、支持力的变化;物块受弹簧弹力和地面对物块的支持力以及拉力F的合力与重力和摩擦力的合力平衡。
【解答】解:A、因为拉力变为F+ΔF时,物块仍处于静止状态,所以弹簧的伸长量不变,则弹簧的弹力不变,故A错误;
B、如果静摩擦力方向向右,对物块受力分析如图:
小物块在水平方向上:F+f=F弹cosθ,
即:f=F弹cosθ﹣F,
随着F的增大f逐渐减小为零,F再增大后摩擦力将反向增大,这时静摩擦力方向向左,大小可以增大到和初始摩擦力大小相等,故B正确;
C、在竖直方向上:mg=F弹sinθ+FN;
可见地面的支持力FN与拉力F无关,F弹不变化,支持力保持不变,故C错误;
D、弹簧弹力和地面对物体的支持力以及拉力F的合力,这三个力的合力与地面给物块的静摩擦力和物块的重力的合力相平衡,由B可知摩擦力大小可能不变,故摩擦力和重力的合力大小可能不变,弹簧弹力和地面对物块的支持力以及拉力F的合力大小可能不变,故D错误。
故选:B。
30.如图所示,把一重为G的物体用一水平方向的推力F=kt(k为恒量,t为时间)压在竖直的足够高的平整墙上,从t=0开始物体所受的摩擦力f随t变化的关系是图中的( )
A. B.
C. D.
【分析】由题意可知,随着时间的推移,压力不断增大,导致物体从滑动到静止。则物体所受的摩擦力先是滑动摩擦力后是静摩擦力。而滑动摩擦力的大小与推物体的压力大小成正比,而静摩擦力的大小与重力大小相等。
【解答】解:如题目中图所示,从t=0开始水平推力F=kt,即压力不断增大,则物体受到滑动摩擦力作用,所以滑动摩擦力的大小与压力正比。
因此滑动摩擦力不断增大。当物体的最大静摩擦力大于重力时,物体开始做减速运动,直到减速到零,由对称性可知,物体的加速度为g,即此时的摩擦力为2G,此时物体处于静止状态,即使推力增大,也不会影响物体的静摩擦力大小。
则有静摩擦力的大小等于重力,故C正确,ABD错误;
故选:C。
31.在中学秋季田径运动会上,高一2班李好同学奋力拼搏,勇夺男子100m冠军,下图为该同学奔跑途中的两个瞬间,用Ff1、Ff2分别表示该同学在图甲、乙两瞬间所受到的摩擦力,则关于Ff1、Ff2的方向,以下说法正确的是( )
A.Ff1向后,Ff2向后 B.Ff1向前,Ff2向前
C.Ff1向前,Ff2向后 D.Ff1向后,Ff2向前
【分析】运动员在奔跑时,后脚用力蹬,则人会向前运动,此时地面给它有个向前摩擦力。而前脚向前跨着地时,正是由于地面对它有个向后的摩擦力,才使前脚不会向前滑动。
【解答】解:当该同学奔跑途中,后脚用力向后蹬,人才向前运动,正是由于地面给后脚有个向前的静摩擦力,即Ff1向前,使运动员能向前运动;
而当前脚向前跨时,正是由于地面给前脚有个向后的静摩擦力,否则运动员会向前滑动,所以前脚受到地面的向后静摩擦力,即Ff2向后,故C正确,ABD错误。
故选:C。
32.如图所示,有一小球被轻绳拴住悬挂在天花板上并放置在斜面上,已知轻绳与竖直方向的夹角为45°,斜面倾角为37°,所有接触面都是光滑的,在斜面上施加一水平外力,使整个装置开始处于静止状态。现水平向左缓慢移动斜面,直至轻绳到达竖直位置,该过程中小球一直在斜面上,小球视为质点。下列说法正确的是( )
A.斜面开始静止时,轻绳对小球的拉力大小等于斜面对小球的支持力大小
B.斜面缓慢移动过程中,斜面对小球的支持力先增大后减小
C.斜面缓慢移动过程中,轻绳对小球的拉力一直增大
D.斜面缓慢移动过程中,斜面对水平面的压力一直不变
【分析】对小球受力分析,按力的正交分解,根据平衡条件列方程求解;然后结合角度的变化判断。
【解答】解:A、对小球受力分析,设小球受到的重力为G,将拉力T和支持力FN沿水平和竖直方向分解,如下图
水平方向上:Tsin45°=FNsin37°①
竖直方向上:Tcos45°+FNcos37°=G②
联立①②解得:FN=,T=<FN,故A错误;
BC、分析小球的受力情况,如图所示
斜面缓慢向左运动过程中,细线与竖直方向的夹角不断减小,由图可看出,拉力T逐渐增大,支持力N逐渐减小,B错误,C正确;
D、设绳子与竖直方向夹角为θ,利用整体法,竖直方向有
FN+Tcosθ=G总
由于水平向左缓慢移动斜面,θ减小且拉力T逐渐增大,可知水平面对斜面的支持力逐渐减小,由牛顿第三定律可知斜面对水平面压力减小,D错误。
故选C。
二.解答题(共3小题)
33.如图所示,两木块的质量分别为m1和m2,两轻质弹簧的劲度系数分别为k1和k2,上面的木块压在上面的弹簧上(但不拴接),整个系统处于平衡状态.现缓慢地向上提上面的木块,直到它刚离开上面的弹簧,求:
(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
【分析】系统原来处于平衡状态,两个弹簧均被压缩,弹簧k2的弹力等于两物体的总重力.缓慢向上提上面的木块,直到它刚离开上面弹簧时弹簧k2的弹力等于m2g,根据胡克定律分别求出下面弹簧两种状态下压缩的长度,下面木块移动的距离等于弹簧两种状态下压缩的长度之差.
【解答】解:(1)m1离开弹簧后,下面弹簧的弹力F=m2g=k2Δx,所以压缩量Δx=
(2)设下面弹簧受到的弹力为F2,压缩量为Δx2,上面弹簧受到的弹力为F1,压缩量为Δx1,
由物体的平衡及胡克定律有:F2=(m1+m2)g,
Δx2=
F1=m1g,Δx1=
所以平衡时总长为L=L1+L2﹣Δx1﹣Δx2
=L1+L2﹣﹣.
当上面的物体刚离开时总长为L′=L1+L2﹣Δx=L1+L2﹣
所以上面物体移动的距离ΔL=L′﹣L=+﹣=
答:(1)m1离开弹簧后,下面弹簧的压缩量;
(2)这个过程中上面木块移动的距离.
34.如图所示,质量为m1的物体A压在放于地面上的竖直轻弹簧k1上,上端与轻弹簧k2相连,轻弹簧k2上端与质量为m2物体B相连,物体B通过轻绳跨过光滑的定滑轮与轻质小桶P相连,A、B均静止.现缓慢地向小桶P内加入细砂,当弹簧k1恰好恢复原长时,(小桶一直未落地)求
(1)小桶P内所加入的细砂质量;
(2)小桶在此过程中下降的距离.
【分析】(1)当弹簧k1恰好恢复原长时,对AB组成的整体,由平衡条件求出绳子的拉力,从而求得小桶P内所加人的细砂质量.
(2)先研究开始时弹簧k1的压缩量和弹簧k2的压缩量,再研究k1恢复原长时弹簧k2的伸长量,由几何关系得到小桶在此过程中下降的距离.
【解答】解:(1)当k1恢复原长时,对AB整体分析,绳子的拉力为 F=(m1+m2) g,即小桶中细砂的质量为m1+m2.
(2)开始时,对AB分析,k1x1=(m1+m2)g,弹簧k1的压缩量为:
x1=
对B分析,k2x2=m2g,弹簧k2的压缩量为:
x2=
当k1恢复原长时,对A分析,k2x2′=m1g,弹簧k2的伸长量为:
x2′=
在此过程中,小桶下降的距离为:
h=x1+x2+x2′=(m1+m2)g
答:(1)小桶P内所加入的细砂质量是m1+m2;
(2)小桶在此过程中下降的距离是(m1+m2)g.
35.如图所示,一劲度系数为k1的弹簧,竖直地固定在桌面上,上面压一质量为m的物体,另一劲度系数为k2的弹簧竖直放在物体上面,其下端与物体的上表面连接在一起,两个弹簧的质量都不计。要使下面弹簧的弹力减为原来的时,应将上面弹簧的上端A竖直向上提高多少?
【分析】对物体受力分析,有平衡条件可求弹簧的形变量,上面弹簧的上端A竖直向上提高的距离为两弹簧的形变量之和。
【解答】解:若下面弹簧处于压缩状态,则下面弹簧弹力的变化量为mg,
根据k== 知,下面弹簧的形变量的变化量为:Δx1=,
对物体分析有:上面弹簧的弹力为:F2=mg﹣mg=mg,
则上面弹簧形变量为:Δx2==,
则有:d=Δx1+Δx2=mg()。
若下面弹簧处于伸长状态,则下面弹簧弹力的变化量为 mg,
则下面弹簧形变量的变化量Δx1=,
对物体分析有:上面弹簧的弹力F2=mg+mg=mg,
则上面弹簧的Δx2==,
则d=Δx1+Δx2=mg(+ )。
答:应将上面弹簧的上端A竖直向上提高mg()或mg(+ )。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
